算法学习——从零实现循环神经网络

从零实现循环神经网络

• 一、任务背景
• 二、数据读取与准备
• • [1. 词元化](#1. 词元化)
  • [2. 构建词表](#2. 构建词表)
• 三、参数初始化与训练
• • [1. 参数初始化](#1. 参数初始化)
  • [2. 模型训练](#2. 模型训练)
• 四、预测
• 总结

一、任务背景

对于序列文本来说，如何通过输入的几个词来得到后面的词一直是大家关注的任务之一，即：通过上文来推测下文的内容。如果通过简单的MLP来进行预测的话，似乎不会得到什么好的结果，所以科学家针对序列数据设计了循环神经网络架构（Recurrent Neural Network, RNN）。

------图片来源：书籍《动手学习深度学习》李沐等

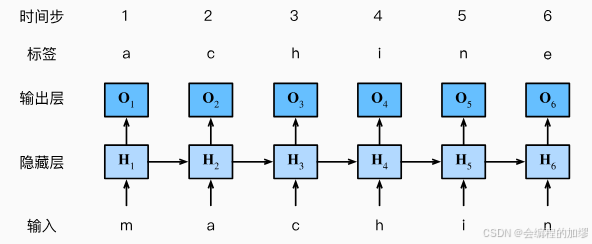
RNN在之前的基础上将上一时刻的隐状态作为这一时刻的隐状态的输入，即： H t = X W + H t − 1 H_{t}=XW+H_{t-1} Ht=XW+Ht−1，从而预测这一时刻的输出，由于不同的时间步长可能有不同的结果，所以在进行此类任务时需要将时间步长也作为预先设定的超参数，例如：预测特定步长的后续的句子

------图片来源：书籍《动手学习深度学习》李沐等

当然，我上面描述的内容似乎不太诱人，时至今日，基于Transformer架构的ChatGPT已经发展的十分迅速了，但是我认为学习RNN可以更好地帮助我们理解Transformer设计的巧妙之处，

⭐ 本文主要是将具体的代码实现，因此不在原理方面进行过多赘述，如果大家对原理感兴趣可以查看其他博客或与我交流讨论！

二、数据读取与准备

在进行一个模型的学习之前，我们首先要知道模型的输入是什么？对于保存了一本书的.txt而言，如果直接把这本书输入到模型中，那么模型如果学习具体东西呢？或者说模型怎么学习字符数据而不是像线性模型那样的数值数据呢？

因此，第一步是需要准备一个词表，将输入的字符转换成与词表对应的数字数据。

1. 词元化

为了更好地对数据进行编码和处理，这里没有选择将每个单词作为一个词表，而是将每个字符作为词表，因此词元化时，是将每个字符分开的：

with open(File_path) as f:
    lines = f.readlines()

lines = [re.sub('[^A-Za-z+]', ' ', line).strip().lower() for line in lines]  # 文本预处理
tokens = [list(line) for line in lines]

类似于下面这样：

2. 构建词表

根据词元出现的词频，将这些字符按照出现的频率进行排序，同时识别不了的字符就用一些特定的符号进行代替<unk>，从而形成两个主要的数据，这两个数据用于将字符和数字相互转换：

• 列表：idx_to_token（即可以通过索引来找到对应的词）
• 字典：token_to_idx（通过词来查到具体的索引）

### 获取词表 vocab ###
tokens = [token for line in tokens for token in line]  # 所有字符展平成一列

counter = collections.Counter(tokens)
token_freqs = sorted(counter.items(), key=lambda x: x[1],    # 按出现频次排序，形成一个词表（英文字母）
                                   reverse=True)
reserved_tokens = []
idx_to_token = ['<unk>'] + reserved_tokens
# 字典 ---> 通过token找索引
token_to_idx = {token: idx for idx, token in enumerate(idx_to_token)}

min_freq = 0

for token, freq in token_freqs:   # 迭代频率词表，构建两个索引
    if freq < min_freq:
        break
    if token not in token_to_idx:
        idx_to_token.append(token)
        token_to_idx[token] = len(idx_to_token) - 1

vocab = {'idx_to_token':idx_to_token,  # 这个词表很重要
         'token_to_idx':token_to_idx}

字符出现的频率：

词表：

最后，将所有词元化的数据通过这个词表，转换为数字的形式：

### 构建语料库 corpus ###

corpus = [vocab['token_to_idx'][token]  for line in tokens  for token in line]
# print(corpus[:10])

# 获取足够多的数据
maxtokens = 10000 
if maxtokens > 0:
    corpus = corpus[:maxtokens]

三、参数初始化与训练

因为我直接将所有代码拆开来看，所以不会单独写一个模型的类或函数，因此直接跳过模型构建的过程。在训练的流程中，能更清除地看到模型具体是哪一个，以及参数是如果更新。

1. 参数初始化

首先，要有效地训练模型我们需要对其参数进行初始化，那么这里可以列出RNN的数学表达式，以便我们知道其有些什么参数：

假设，输入的小批量数据为 X p X_{p} Xp， t t t时刻的输出为 O t O_{t} Ot，则有：
H t = X t W x h + H t − 1 W h h + b h (1) H_{t}=X_{t}W_{xh}+H_{t-1}W_{hh}+b_{h} \tag{1} Ht=XtWxh+Ht−1Whh+bh(1)
O t = H t W h q + b q (2) O_{t}=H_{t}W_{hq}+b_{q} \tag{2} Ot=HtWhq+bq(2)

其中， H H H 表示隐状态， b b b 表示偏置， W W W 表示权重

因此可以看到，可学习的参数包括： W x h 、 W h h 、 W h q 、 b h 、 b q W_{xh}、W_{hh}、W_{hq}、b_{h}、b_{q} Wxh、Whh、Whq、bh、bq

因此，对这些参数进行初始化：

### 参数初始化 ###
num_inputs = num_outputs = vocab_size
# 隐藏层参数
W_xh = torch.randn(size=(num_inputs, num_hiddens), device=device) * 0.01
W_hh = torch.randn(size=(num_hiddens, num_hiddens), device=device) * 0.01
b_h = torch.zeros(num_hiddens, device=device)

# 输出层参数
W_hq = torch.randn(size=(num_hiddens, num_outputs), device=device) * 0.01  # 这里没缩放
b_q = torch.zeros(num_outputs, device=device)

params = [W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
    param.requires_grad_(True)   # 初始化时，参数的grad为None

与其他的模型不同，RNN中需要初始化上一时刻的隐状态 H t − 1 H_{t-1} Ht−1，当 t = 1 t=1 t=1时， H t − 1 H_{t-1} Ht−1自然为0：

init_state = (torch.zeros((batch_size, num_hiddens), device=device), )

2. 模型训练

模型训练过程代码如下：

for epoch in range(num_epochs):
    state, timer = None, Timer()
    metric = Accumulator(2)
    ### 制作可迭代数据 ###
    offset = random.randint(0, num_steps)  # 随机偏移
    num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
    # print(f'offset:{offset},num_tokens: {num_tokens}')
    # 选择x数据
    Xs = torch.tensor(corpus[offset: offset + num_tokens])   # [9952]
    Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])  # [9952]

    Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)  # [32,311]相当于将其分为32份
    # print(Xs.shape, Ys.shape)
    num_batches = Xs.shape[1] // num_steps   # 8
    # print(f'num_batches: {num_batches}')
    for i in range(0, num_steps * num_batches, num_steps):
        X = Xs[:, i: i + num_steps]   # [32, 35]
        Y = Ys[:, i: i + num_steps]   # [32, 35]
        # 这里就相当于for X, Y in train_iter
        # print(X, Y)
        if state is None:
            state = init_state
        else:
            for s in state:
                s.detach_()
        y = Y.T.reshape(-1)   # 1120 = 32 * 35, 把y展平成一维
        X, y = X.to(device), y.to(device)
        X = F.one_hot(X.T, vocab_size).type(torch.float32)  # [35, 32, 28]  28是one hot 编码的维度
        
        W_xh, W_hh, b_h, W_hq, b_q = params
        H, = state  
        outputs = []
        for input in X:
            H = torch.tanh(torch.mm(input, W_xh) + torch.mm(H, W_hh) + b_h)
            Y = torch.mm(H, W_hq) + b_q   # [32, 28]
            outputs.append(Y)
        y_hat, state = torch.cat(outputs, dim=0), (H,)  # 35
        # y_hat, state = rnn(X, state, params)
        l = loss(y_hat, y.long()).mean()  # 计算出损失
        l.backward()   # 更新的是params的梯度
        ### 梯度裁剪 ###
        norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
        theta = 1
        if norm > theta:
            for param in params:
                param.grad[:] *= theta / norm
        ### updater 梯度更新 ###
        with torch.no_grad():
            for param in params:  
                param -= lr * param.grad    # 参数在这里进行更新, 不用除以batch_size
                param.grad.zero_()    # 将梯度置零
        metric.add(l * y.numel(), y.numel())
    ppl, speed = math.exp(metric[0] / metric[1]), metric[1] / timer.stop()
    loss_value.append(ppl)
    if (epoch+1) % 10 == 0:  
        print(f'=========epoch:{epoch+1}=========Perplexity:{ppl}=======speed:{speed}=======')

x = range(0, 500)
plt.plot(x, loss_value)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

需要注意以下几点：

• 每一轮训练都需要将初始状态设置为0，因此在一开始设置了state=None

• 在将X输入模型中时，采用的是独热编码（one-hot），即根据词表，每一列形成28个0/1值（28=26个英文字母+空格+'unk'）

训练损失（困惑度, perplexity）曲线如下：

四、预测

代码如下，执行预测时需要注意：

• 记得将batch_size设置为1，因为预测的数据没有分成不同的batch_size
• 预热期的作用：一是输入待预测的单词后面，如本例中的'traveller'，二是让隐状态进行更行，方便能预测出更好的结果

batch_size = 1  # 训练时得batch_size
state = (torch.zeros((batch_size, num_hiddens), device=device), )
prefix = "traveller"
num_preds = 50   # 预测步长
outputs_pre = [vocab['token_to_idx'][prefix[0]]]
get_input = lambda: torch.tensor([outputs_pre[-1]], device=device).reshape((1, 1))
for y in prefix[1:]:  # 预热期
    inputs = get_input()
    X = F.one_hot(inputs.T, vocab_size).type(torch.float32) # [1, 1, 28]
    W_xh, W_hh, b_h, W_hq, b_q = params_frezon
    H, = state  # [1, 512]
    outputs = []
    for x in X:   # X [1, 28]，相当于把时间步长抽离出来
        H = torch.tanh(torch.mm(x, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q   # [1, 28], 得到的值是小数咋整？应该要处理一下吧
        outputs.append(Y)
    _, state = torch.cat(outputs, dim=0), (H,)  # state[1, 512]
    # _, state = rnn(X, state, params_frezon)
    outputs_pre.append(vocab['token_to_idx'][y])

for _ in range(num_preds):
    inputs = get_input() 
    X = F.one_hot(inputs.T, vocab_size).type(torch.float32) # [1, 1, 28]
    W_xh, W_hh, b_h, W_hq, b_q = params_frezon
    H, = state   # 保留预热期的H
    outputs = []
    for x in X:   # X [1, 1, 28]，相当于把时间步长抽离出来
        H = torch.tanh(torch.mm(x, W_xh) + torch.mm(H, W_hh) + b_h) # [1, 512]
        Y = torch.mm(H, W_hq) + b_q   # [1, 28], 得到的值是小数咋整？应该要处理一下吧
        outputs.append(Y)
    y, state = torch.cat(outputs, dim=0), (H,)   # y [1， 28], state [1, 512]
    # y, state = rnn(X, state, params_frezon)
    outputs_pre.append(int(y.argmax(dim=1).reshape(1)))  # 这里将小数变成整数
# y.argmax用于返回指定维度上最大值的索引位置
# print(outputs_pre)
# print(vocab['idx_to_token'][3])
# predict = [vocab['idx_to_token'][i] for i in outputs_pre]
predict = ''.join([vocab['idx_to_token'][i] for i in outputs_pre])
print(predict)

总结

这个代码实现起来整体比较简单，就是输入数据那里需要多多理解，把输入与输出梳理明白。模型完全可以套着公式来看代码，与MLP最大的区别就是多了一个state的更新和相应的可学习权重 W h h W_{hh} Whh。

完整的代码和数据我放在gitee网站上面了，有需要的朋友直接自取即可： gitee仓库