文章目录
[一 摘要](#一 摘要)
[二 资源](#二 资源)
[三 内容](#三 内容)

一 摘要
平面检测是许多应用的关键组件,例如工业逆向工程和自动驾驶汽车。然而,现有的平面检测技术对噪声和用户定义的参数很敏感。作者引入了一种快速确定性技术,用于在无组织的点云中进行平面检测,该技术对噪声具有鲁棒性,并且几乎独立于参数调整。它基于从稳健统计数据中提取的新型平面度检验以及拆分和合并策略。其参数值会自动调整以适应输入数据集中样本的局部分布,从而有助于对较小的平面区域进行良好的重建。我们在几个真实数据集上展示了我们的解决方案的有效性,将其性能与最先进的平面检测技术进行了比较,并表明它实现了更高的准确性,同时仍然是最快的解决方案之一。
二 资源
文章:A Robust Statistics Approach for Plane Detection in Unorganized Point Clouds
代码:https://github.com/qq625924821/PlaneDetection
日期:2019年
三 内容

1)摘要
平面检测是许多应用的关键组件,例如工业逆向工程和自动驾驶汽车。然而,现有的平面检测技术对噪声和用户定义的参数很敏感。作者引入了一种快速确定性技术,用于在无组织的点云中进行平面检测,该技术对噪声具有鲁棒性,并且几乎独立于参数调整。它基于从稳健统计数据中提取的新型平面度检验以及拆分和合并策略。其参数值会自动调整以适应输入数据集中样本的局部分布,从而有助于对较小的平面区域进行良好的重建。我们在几个真实数据集上展示了我们的解决方案的有效性,将其性能与最先进的平面检测技术进行了比较,并表明它实现了更高的准确性,同时仍然是最快的解决方案之一。
2)创新点
①一种在无组织的点云中检测平面的技术,它对噪声具有鲁棒性,并且几乎独立于参数调整。比以前的技术更准确,同时计算效率更高;
②一种基于稳健统计的新型平面度测试,与现有解决方案相比,它对点云噪声尺度的依赖性更小。它允许直接应用于包含不同和可变噪声级别的点云;
③一种迭代增长-合并过程,能够以极高的精度和细节检索连接的平面区域。该技术能够自动划定检测到的平面区域;
④一种自动调整平面检测参数以适应数据集中样本的局部分布的机制 。
3)算法结构

用于平面检测的区域增长算法基于稳健的统计数据,包括三个主要步骤:split、grow 和 merge。在分割阶段,使用八叉树对输入点云进行空间细分,直到叶节点的样本少于 n 个。如果八叉树叶节点中的样本通过我们的鲁棒噪声平面性测试,它们将经历一个生长过程,并且可以进一步与相邻平面对象合并成更大的平面斑块。在增长阶段,通过平面度测试的块将被增强,以填补分割阶段留下的可能空白。但是,增长参数(到平面的最大距离和最大法向偏差)是根据数据分布自动估计的。最后,在合并阶段,根据某个边界条件合并补丁。Grow 和 Merge 阶段将迭代,直到所有patch都变得稳定,即不可能进一步增长。整个过程的输出由检测到的一组分隔平面区域组成。该管道的简化版本如上图所示。
A split

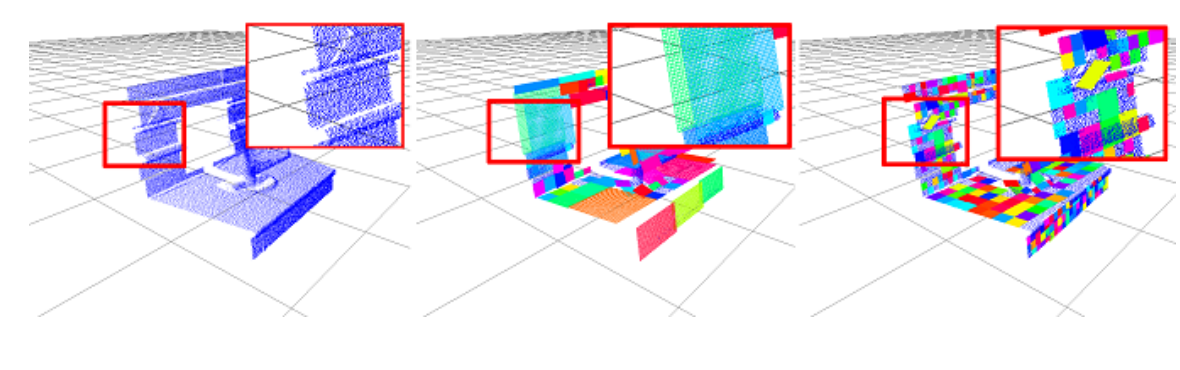
首先检测点云中的最小平面区域(patch)。为了检测这些区域,它需要一种分区技术和一个平面性测试。包含整个点云的八叉树用于递归细分空间,直到每个单元格包含的样本少于n样本,这在经验上被定义为样本总数的 0.1%。然后从叶子一直到根部进行平面性测试,每当检测到平面斑块时停止。检测后,样品进入生长步骤。如果与父 octree 节点关联的所有 8 个单元都未通过平面性测试,则父节点本身将成为新的 octree 叶节点(替换其 8 个子节点)并接受平面性测试。此过程以递归方式应用。这种策略允许检测精细细节,如下图 (右) 所示。检测到的平面patch的数量不是问题,因为它们稍后将合并。
B Robust planarity test
快速平面估计通常采用PCA方法,然而。PCA方法主要依赖数据的均值和标准差,而这两者都受噪声影响。因此,传统PCA算法受噪声影响。而Robust-PCA其处理效率较低,难以应用百万级的点云数据。
考虑到抗噪性,采用中位数替换均值,同时,采用中位数绝对偏差替换标准差:

其中,k=1.4826。
确定一个平面,通常采用点法式(C,N)确定。C为平面上一点,可用中位数,N为法向量,可用各样本法向量的中位数确定:


提出了三种稳健的检验来评估估计平面的质量:平面样本距离检验 (T1)、平面样本法向偏差检验 (T2)、和异常值百分比检验 (T3)
b1 Plane-sample distance test


其中,C和N分别为前期介绍的坐标中位数和法向量中位数。
根据统计学中3σ原理,可设置区间为:

其中,α=3。
由于处理的是到平面的 距离,因此此区间的上限表示样本在被视为异常值之前可以到达平面的最大距离。将此上限称为到平面的最大距离 (MDP)。
当考虑一组近似共面的样本时,值 MDP = 3×MAD 可能会在包含高噪声水平的数据集中假设不合理的较大值。因此,会自动估计相对于patch尺寸的自适应距离阈值。
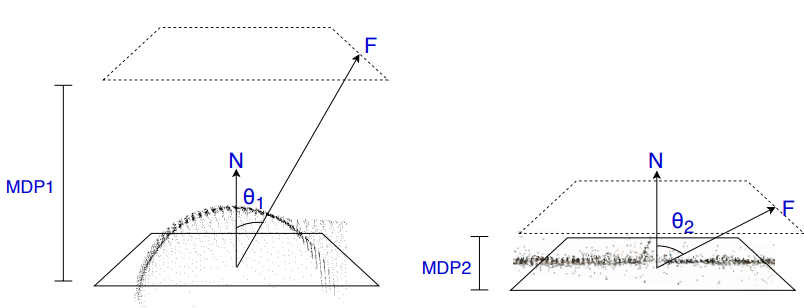
如上图所示,曲面产生的 MDP 值较大(左),而平面产生的 MDP 值较小(右)。对于相同大小的patch,较大的 MDP 值会导致 F 和 N(平面法线)之间的角度 θ 较小。其中:


利用这一观察结果来评估样本位置相对于面片尺寸的差异,作为适用于不同点云配置的角度阈值。这样,用户就无需提供或调整参数值来改进平面检测。较大的面片可以接受更多的样本方差(即更大的 MDP),这由角度阈值 θ 捕获。通过实验,发现 θ > 75◦ 提供了一个保守的角度阈值,该阈值为所有测试数据集生成良好结果。
b2 Plane-sample normal deviation test



同样,设置 α = 3,并且只对 IΦ 的上限感兴趣。将此上限称为最大法向偏差 (MND),并丢弃 MND 高于某个阈值的平面。与 MDP 不同,MND 不依赖于面片尺寸。通过实验,发现 MND < 60◦ 为所有测试数据集提供了良好的结果。
b3 Outlier percentage test
对于任何给定的面片,如果其至少 25% 的样本被视为异常值(即,超出区间 ID 或 IΦ),则该平面被认为为非平面,因此被丢弃。
C grow
由于点云被划分为八叉树单元,一些共面样本可能正好落在生成给定平面面片的体素之外。此外,由于局部噪声,某些面片可能已被丢弃。无论哪种情况,都需要增长检测到的平面面片以填充可能的空白以提供更准确的平面检测。检测到的平面面片 Pi 具有三个属性:由对 (Ci , Ni) 定义的估计平面;其到平面的最大距离 (MDPi)及其最大法向偏差 (MNDi)。为了增加平面面片,为整个点云定义了一个邻域图 G,其中图形的每个顶点代表一个样本,每条边连接使用 k 个最近邻(使用 k = 50)标识的两个相邻样本。创建邻域图后,执行广度优先搜索,从对应于面片 Pi 样本的顶点开始。如果满足以下条件,则访问的样本将添加到 Pi 中:(i) 它不属于任何其他面片,并且 (ii) 它满足 Pi 的 inlier 条件。Pi 的离群值条件必须满足两个条件:(i) 样本 j 到 Πi 的距离应小于 MDPi(即 dj = |(Pj−Ci)·Ni |< MDPi);(ii) 样本法向量与 Ni 之间的偏差应小于 MNDi(即 φj = acos((|Nj · Ni|)< MNDi)。与以前的区域增长方法不同,其内部条件依赖于样本到平面距离和法向偏差的固定阈值,我们的方法不对点云的尺度或噪声水平做出任何假设,因为计算出的稳健统计已经考虑了它们。由于样本可能满足多个 patch inlier 条件,因此有必要在 patchs 之间建立一些优先级。因此,在开始生长阶段之前,patch按其最大法向偏差升序排序。这样,噪点最少的块将首先增长,并有机会变得更大。整个生长阶段总结在下列算法伪代码中。

D merge

在相邻 octree 节点处检测到的补丁可能会形成单个平面,在这种情况下,应合并。要合并的两个补丁 A 和 B,它们必须满足三个合并条件:(M1) 它们应该是相邻的(即,邻域图 G 应该包含至少一条将 A 的样本连接到 B 的样本的边);(M2) A 和 B 的估计法线应具有相似的方向(即,这两个法线之间的角度应小于 max(MDNA,MDNB));并且 (M3) A 中至少有一个样本应满足 B 的内值条件(反之亦然)。虽然前两个条件是不言而喻的,但第三个条件可以防止彼此不够接近的平行面片的合并。这些条件如上图所示。使用 union-find 数据结构来快速创建和查找合并面片组。然后,合并过程会获取满足三个合并条件的每组面片,并返回一个统一的面片。
E Iterative Grow-Merge Procedure
合并一组面片后,生成的面片可能需要重新估计其关联的平面,以及其距离 (D) 和法向偏差 (Φ) 的分布。然而,由于稳健估计器(中位数和 MAD)的分割点是 50%,因此只有当面片扩展到其原始样本数的 50% 以上时,才需要更新。在这种情况下,需要重新执行增长和合并步骤,因为新面片的 inlier 条件可能已相对于其以前的状态发生变化。当没有面片需要更新时(即,当所有面片都稳定时),此迭代过程将停止。为了减少更新次数,每当需要合并一组面片时,都会选择样本最多的面片作为组代表。
4)实验
A dataset


B 对比方法
3D霍夫变换、RANSAC、区域增长。
C 对比结果

评估技术在每个数据集上的性能。检测到的平面数与平面总数 (#)、精度 (P)、召回率 (R)、F1 分数 (F1)、处理时间(以秒为单位) (T(s))。最佳结果以粗体突出显示。

考虑所有数据集的评估技术的平均性能。平均平面检出率 (A%)、平均精度 (AP)、平均召回率 (AR)、平均精度和平均召回率的 F1 分数 (AF1)、平均标准化时间(标准化时间:以毫秒为单位的处理时间除以样本数) (ANT)。按 AF-1 评分排序的技术。最佳结果以粗体突出显示。

通过比较技术检测到的所有数据集的平面。Ground Truth 显示在最右侧的列中。对于每对技术和数据集,检测到的平面都使用不同的颜色突出显示。黑点表示被每种技术视为异常值的样本。
5)结论
提出了一种强大的 O(n log n) 技术,用于检测无序点云中的平面,该技术在平均精度、召回率和 F1 分数方面比以前的方法具有更好的精度,同时仍然是最快的方法之一。为此,引入了一种基于稳健统计的新型稳健平面度检验,该检验对噪声不太敏感,从而为基于 PCA 的最常用程序提供了很好的替代方案。还引入了一个迭代增长-合并策略,能够以极高的精度和细节检测划定的平面区域。该方法鲁棒于噪且不需要参数调优。
通过与最流行的和最新的平面检测方法进行详细比较来证明技术的有效性,其中包括基于霍夫变换、RANSAC 和区域生长的方法。这些技术在选定的 7 个数据集上进行了评估,这些数据集涵盖了大量不同的特性,例如样本数量、样本密度、噪声水平、平面数量和不同的采集传感器。本文技术在所有数据集上都表现良好,取得了最佳的平均结果。在此类评估中,所有其他技术使用的参数已针对每个特定数据集单独调整,以在每种情况下产生最佳结果。另一方面,该技术会根据局部样本分布自动调整其参数值。目前,只执行局部平面性测试,而忽略了点云的全局结构。这可能有助于检测大型弯曲结构上的假平面(例如,检测沿半径相对较大的圆柱形元件轴的矩形截面)。通过分析曲面片的父 octree 节点内的曲面曲率,并防止在曲面中检测局部平面曲面片,可以缓解此问题。