目录
- [0 专栏介绍](#0 专栏介绍)
- [1 最小控制问题一般形式](#1 最小控制问题一般形式)
- [2 边界中间值问题](#2 边界中间值问题)
-
- [2.1 问题形式化](#2.1 问题形式化)
- [2.2 优化求解](#2.2 优化求解)
- [3 算法仿真](#3 算法仿真)
-
- [3.1 C++实现](#3.1 C++实现)
- [3.2 Python仿真](#3.2 Python仿真)
0 专栏介绍
🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
🚀详情:运动规划实战进阶:轨迹优化篇
1 最小控制问题一般形式
优化变量 z ∈ R m z \in \mathbb{R}^m z∈Rm的最小控制优化问题的一般性数学描述为:
min z ( t 0 ) , t = t k ∫ t 0 t k v ( t ) T W v ( t ) + ρ ( t k − t 0 ) s.t. G ( z ( t ) , ⋯ , z ( s ) ( t ) ) ⩽ 0 , ∀ t ∈ [ t 0 , t k ] z ( t ) ∈ C , ∀ t ∈ [ t 0 , t k ] z [ s − 1 ] ( t i ) = z ˉ i , 1 ⩽ i ⩽ k , r i ⩽ s z [ s − 1 ] ( t 0 ) = z ˉ 0 , z [ s − 1 ] ( t k ) = z ˉ k \begin{aligned} \min_{z(t_0), t=t_k} \quad & \int_{t_0}^{t_k} \boldsymbol{v}(t)^T \boldsymbol{W} \boldsymbol{v}(t) + \rho(t_k - t_0) \\ \text{s.t.} \quad & \boldsymbol{G}(z(t), \cdots, z^{(s)}(t)) \leqslant \boldsymbol{0}, \ \forall t \in [t_0, t_k] \\ & z(t) \in \mathcal{C}, \ \forall t \in [t_0, t_k] \\ & z^{[s-1]}(t_i) = \bar{z}_i, \ 1 \leqslant i \leqslant k, \ r_i \leqslant s \\ & z^{[s-1]}(t_0) = \bar{z}_0, \ z^{[s-1]}(t_k) = \bar{z}_k \end{aligned} z(t0),t=tkmins.t.∫t0tkv(t)TWv(t)+ρ(tk−t0)G(z(t),⋯,z(s)(t))⩽0, ∀t∈[t0,tk]z(t)∈C, ∀t∈[t0,tk]z[s−1](ti)=zˉi, 1⩽i⩽k, ri⩽sz[s−1](t0)=zˉ0, z[s−1](tk)=zˉk
其中定义 z [ s − 1 ] ( t ) ≜ ( z T , z ˙ T , ⋯ , z ( s − 1 ) T ) T z^{[s-1]}(t) \triangleq (z^T, \dot{z}^T, \cdots, z^{(s-1)^T})^T z[s−1](t)≜(zT,z˙T,⋯,z(s−1)T)T, v ( t ) ≜ z ( s ) ( t ) \boldsymbol{v}(t) \triangleq z^{(s)}(t) v(t)≜z(s)(t)。 z ( t ) z(t) z(t)是微分平坦空间的输出轨迹, T T T是轨迹分配的总时长。当 s = 2 s=2 s=2时为加速度(acceleration)、 s = 3 s=3 s=3时为加加速度(jerk)、 s = 4 s=4 s=4时为加加加速度(snap)。目标函数期望轨迹高阶微分量 v ( t ) \boldsymbol{v}(t) v(t)尽可能平滑,有利于减少控制输入的突变,降低机械部件的磨损,平滑的轨迹也有益于舒适性的提升;同时运动时间尽可能短。 G ( z ( t ) , ⋯ , z ( s ) ( t ) ) ⩽ 0 \boldsymbol{G}(z(t), \cdots, z^{(s)}(t)) \leqslant \boldsymbol{0} G(z(t),⋯,z(s)(t))⩽0是优化问题的不等式约束,例如约束轨迹符合智能体物理限制。 z ( t ) ∈ C z(t) \in \mathcal{C} z(t)∈C代表安全性约束,即要求运动轨迹不与障碍发生重叠。 z [ s − 1 ] ( t i ) = z ˉ i z^{[s-1]}(t_i) = \bar{z}_i z[s−1](ti)=zˉi是优化问题的中间点约束, z [ s − 1 ] ( t 0 ) = z ˉ 0 z^{[s-1]}(t_0) = \bar{z}_0 z[s−1](t0)=zˉ0 与 z [ s − 1 ] ( t k ) = z ˉ k z^{[s-1]}(t_k) = \bar{z}_k z[s−1](tk)=zˉk是优化问题的边界条件,约束轨迹的首末各阶状态。
2 边界中间值问题
2.1 问题形式化
当第一节中一般优化问题的约束条件仅保留边界约束和中间点约束时,简化为边界中间值问题(Boundary Intermediate Value Problem, BIVP),描述如下:
min ∫ t 0 t k v ( t ) T W v ( t ) + ρ ( t k − t 0 ) s.t. z [ r i − 1 ] ( i − 1 ) ( t i ) = z ^ i , 1 ⩽ i < k , r i ⩽ s ( 8.4 ) z [ s − 1 ] ( s − 1 ) ( t 0 ) = z ^ 0 , z [ s − 1 ] ( s − 1 ) ( t k ) = z ^ k \begin{aligned} \min & \int_{t_0}^{t_k} \boldsymbol{v}(t)^T \boldsymbol{W} \boldsymbol{v}(t) + \rho(t_k - t_0) \\ \text{s.t.} & \ z_{[r_i-1]}^{(i-1)}(t_i) = \widehat{z}i, \ 1 \leqslant i < k, \ r_i \leqslant s \quad (8.4) \\ & \ z{[s-1]}^{(s-1)}(t_0) = \widehat{z}0, \ z{[s-1]}^{(s-1)}(t_k) = \widehat{z}_k \end{aligned} mins.t.∫t0tkv(t)TWv(t)+ρ(tk−t0) z[ri−1](i−1)(ti)=z i, 1⩽i<k, ri⩽s(8.4) z[s−1](s−1)(t0)=z 0, z[s−1](s−1)(tk)=z k
如上定义的BIVP最优解 z ∗ ( t ) : [ t 0 , t k ] → R n z^*(t): [t_0, t_k] \to \mathbb{R}^n z∗(t):[t0,tk]→Rn的充要条件为:
- z ∗ z^* z∗ 的第 i i i段轨迹是 2 s − 1 2s - 1 2s−1 次多项式;
- 边界条件与中间点条件成立;
- z ∗ z^* z∗ 在 t = t i t = t_i t=ti 处满足 r ˉ i − 1 \bar{r}_i - 1 rˉi−1 次连续可微,其中 r ˉ i = 2 s − r i \bar{r}_i = 2s - r_i rˉi=2s−ri;
举例而言,对于 s = 3 s = 3 s=3 且 r i = 1 r_i = 1 ri=1 的Minimum jerk过路径点问题,最优性条件要求轨迹是 n = 2 s − 1 = 5 n = 2s - 1 = 5 n=2s−1=5 次多项式,同时在中间点 t i t_i ti 处满足四阶连续可微,即路径、速度、加速度、加加速度以及更高次的加加速度在分段点连续
2.2 优化求解
根据 BIVP 最优性原理,最优轨迹 z ∗ z^* z∗包含 2 k s 2ks 2ks个未知的多项式参数。考虑到边界条件提供 2 s 2s 2s个约束,中间点条件提供 r i ( k − 1 ) r_i(k-1) ri(k−1)个约束,中间点连续可微条件提供 r ˉ i ( k − 1 ) \bar{r}_i(k-1) rˉi(k−1)个约束,共计 2 k s 2ks 2ks个约束方程,表明 BIVP 的最优轨迹 z ∗ z^* z∗有且只有一条,在应用时可以直接依据边值和中间值约束解析地求解 z ∗ z^* z∗,不需要显式地计算优化问题。
形式化地,设n阶多项式为 z ( t ) = ∑ i = 0 n p i t i z(t)=\sum_{i=0}^{n}p_{i}t^{i} z(t)=∑i=0npiti
p = [ p 0 p 1 ⋯ p n ] T \boldsymbol{p}=\left[\begin{array}{llll}{p_{0}}&{p_{1}}&{\cdots}&{p_{n}}\\\end{array}\right]^{T} p=[p0p1⋯pn]T
是轨迹参数向量。单个多项式曲线过于简单,一段复杂的轨迹通常需要通过设置中间点将轨迹按时间分为 k k k段,每段用最优的 n = 2 s − 1 n=2s-1 n=2s−1 次多项式曲线表示
z i ( t ) = p i T β ( t − t i ) , t i − 1 ≤ t < t i z_{i}(t)=\boldsymbol{p}{i}^{T}\boldsymbol{\beta}(t-t{i}) , t_{i-1}\leq t<t_{i} zi(t)=piTβ(t−ti),ti−1≤t<ti
其中 β ( t ) = [ 1 t t 2 ⋯ t 2 s − 1 ] T \boldsymbol{\beta}(t)=\left[\begin{array}{llll}{1}&{t}&{t^{2}}&{\cdots}&{t^{2s-1}}\\\end{array}\right]^{T} β(t)=[1tt2⋯t2s−1]T。考虑到平坦变量通常不是一维(例如车辆是二维、无人机是四维),将上式在平坦变量维度上进行堆叠,同时引入时间间隔 T i = t i − t i − 1 T_{i}=t_{i}-t_{i-1} Ti=ti−ti−1 ,得到
z i ( t ) = P i T β ( T ) , 0 ≤ T < T i \boldsymbol{z}{i}(t)=\boldsymbol{P}{i}^{T}\boldsymbol{\beta}(T) , 0\leq T<T_{i} zi(t)=PiTβ(T),0≤T<Ti
其中 P i = [ p i , 1 p i , 2 ⋯ p i , m ] ∈ R 2 s × m \boldsymbol{P}{i}=\left[\begin{array}{llll}{\boldsymbol{p}{i,1}}&{\boldsymbol{p}{i,2}}&{\cdots}&{\boldsymbol{p}{i,m}}\\\end{array}\right]\in\mathbb{R}^{2s\times m} Pi=[pi,1pi,2⋯pi,m]∈R2s×m。接着在分段数上堆叠得到完整多项式系数矩阵
P = [ P 1 P 2 ⋮ P k ] ∈ R 2 s k × m \boldsymbol{P}=\left[\begin{array}{l}{\boldsymbol{P}{1}}\\{\boldsymbol{P}{2}}\\{\vdots}\\{\boldsymbol{P}_{k}}\\\end{array}\right]\in\mathbb{R}^{2sk\times m} P= P1P2⋮Pk ∈R2sk×m
根据BIVP最优性原理的边值条件得到2s个边值约束方程
F 0 P 1 = D 0 , E k P k = D k \boldsymbol{F}{0}\boldsymbol{P}{1}=\boldsymbol{D}{0} , \boldsymbol{E}{k}\boldsymbol{P}{k}=\boldsymbol{D}{k} F0P1=D0,EkPk=Dk
其中
F 0 = [ β ( 0 ) ⋯ β ( s − 1 ) ( 0 ) ] T ∈ R s × 2 s \boldsymbol{F}_{0}=\left[\begin{array}{llll}{\boldsymbol{\beta}(0)}&{\cdots}&{\boldsymbol{\beta}^{(s-1)}(0)}\\\end{array}\right]^{T}\in\mathbb{R}^{s\times 2s} F0=[β(0)⋯β(s−1)(0)]T∈Rs×2s
E k = [ β ( T k ) ⋯ β ( s − 1 ) ( T k ) ] T ∈ R s × 2 s \boldsymbol{E}{k}=\left[\begin{array}{llll}{\boldsymbol{\beta}(T{k})}&{\cdots}&{\boldsymbol{\beta}^{(s-1)}(T_{k})}\\\end{array}\right]^{T}\in\mathbb{R}^{s\times 2s} Ek=[β(Tk)⋯β(s−1)(Tk)]T∈Rs×2s
等式右边的边值 D 0 ∈ R s × m \boldsymbol{D}{0}\in\mathbb{R}^{s\times m} D0∈Rs×m 与 D k ∈ R s × m \boldsymbol{D}{k}\in\mathbb{R}^{s\times m} Dk∈Rs×m提前给定。
根据BIVP最优性原理的中间值约束和连续性约束,每个中间点提供 2 s 2s 2s个约束方程:
E i F i \] \[ P i P i + 1 \] = \[ D i 0 r ⃗ i × m \] \\left\[\\begin{array}{ll}\\boldsymbol{E}_{i} \& \\boldsymbol{F}_{i}\\end{array}\\right\]\\left\[\\begin{array}{c}\\boldsymbol{P}_{i} \\\\\\boldsymbol{P}_{i+1}\\end{array}\\right\]=\\left\[\\begin{array}{c}\\boldsymbol{D}_{i} \\\\\\mathbf{0}_{\\vec{r}_{i} \\times m}\\end{array}\\right\] \[EiFi\]\[PiPi+1\]=\[Di0r i×m
其中
D i ∈ R r i × m \boldsymbol{D}{i} \in \mathbb{R}^{r{i} \times m} Di∈Rri×m
E i = [ β ( T i ) ⋯ β ( r i − 1 ) ( T i ) ∣ β ( T i ) ⋯ β ( r ⃗ i − 1 ) ( T i ) ] T ∈ R 2 s × 2 s \boldsymbol{E}{i}=\left[\boldsymbol{\beta}\left(T{i}\right) \cdots \boldsymbol{\beta}^{\left(r_{i}-1\right)}\left(T_{i}\right) \mid \boldsymbol{\beta}\left(T_{i}\right) \cdots \boldsymbol{\beta}^{\left(\vec{r}{i}-1\right)}\left(T{i}\right)\right]^{T} \in \mathbb{R}^{2s \times 2s} Ei=[β(Ti)⋯β(ri−1)(Ti)∣β(Ti)⋯β(r i−1)(Ti)]T∈R2s×2s
F i = [ 0 2 s × r i ∣ − β ( 0 ) ⋯ − β ( r ⃗ i − 1 ) ( 0 ) ] T ∈ R 2 s × 2 s \boldsymbol{F}{i}=\left[\mathbf{0}{2 s \times r_{i}} \mid-\boldsymbol{\beta}(0) \cdots-\boldsymbol{\beta}^{\left(\vec{r}_{i}-1\right)}(0)\right]^{T} \in \mathbb{R}^{2 s \times 2 s} Fi=[02s×ri∣−β(0)⋯−β(r i−1)(0)]T∈R2s×2s
前 r i r_{i} ri 行用于中间值约束;后 r ˉ i \bar{r}_{i} rˉi 行用于连续性约束。进一步,将所有约束方程堆叠可得:
M = [ F 0 0 0 ⋯ 0 E 1 F 1 0 ⋯ 0 0 E 2 F 2 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ F k − 1 0 0 0 ⋯ E k ] ∈ R 2 k s × 2 k s \boldsymbol{M}=\left[\begin{array}{cccc}\boldsymbol{F}{0} & \mathbf{0} & \mathbf{0} & \cdots & \mathbf{0} \\\boldsymbol{E}{1} & \boldsymbol{F}{1} & \mathbf{0} & \cdots & \mathbf{0} \\\mathbf{0} & \boldsymbol{E}{2} & \boldsymbol{F}{2} & \cdots & \mathbf{0} \\\vdots & \vdots & \vdots & \ddots & \vdots \\\mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots & \boldsymbol{F}{k-1} \\\mathbf{0} & \mathbf{0} & \mathbf{0} & \cdots & \boldsymbol{E}{k}\end{array}\right] \in \mathbb{R}^{2 k s \times 2 k s} M= F0E10⋮000F1E2⋮0000F2⋮00⋯⋯⋯⋱⋯⋯000⋮Fk−1Ek ∈R2ks×2ks
D = [ D 0 D 1 0 ⋮ D k − 1 0 D k ] ∈ R 2 k s × m \boldsymbol{D}=\left[\begin{array}{c}\boldsymbol{D}{0} \\\boldsymbol{D}{1} \\\mathbf{0} \\\vdots \\\boldsymbol{D}{k-1} \\\mathbf{0} \\\boldsymbol{D}_{k}\end{array}\right] \in \mathbb{R}^{2 k s \times m} D= D0D10⋮Dk−10Dk ∈R2ks×m
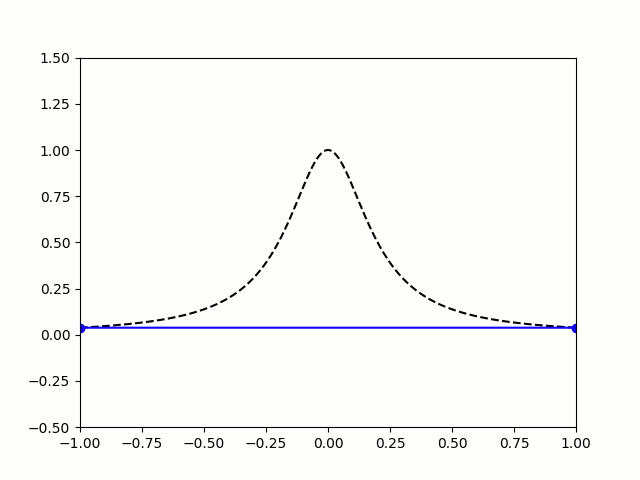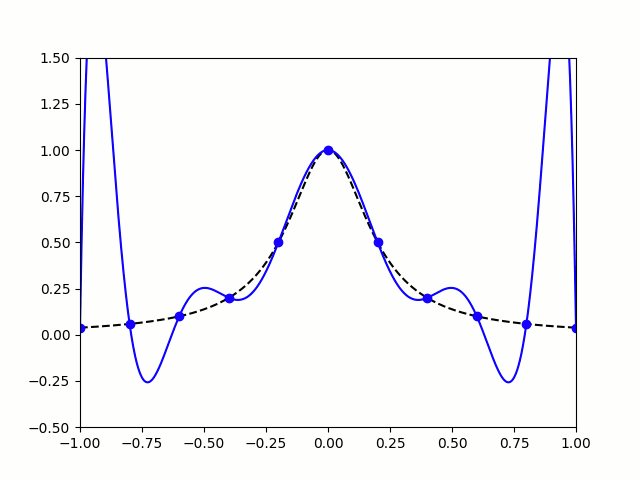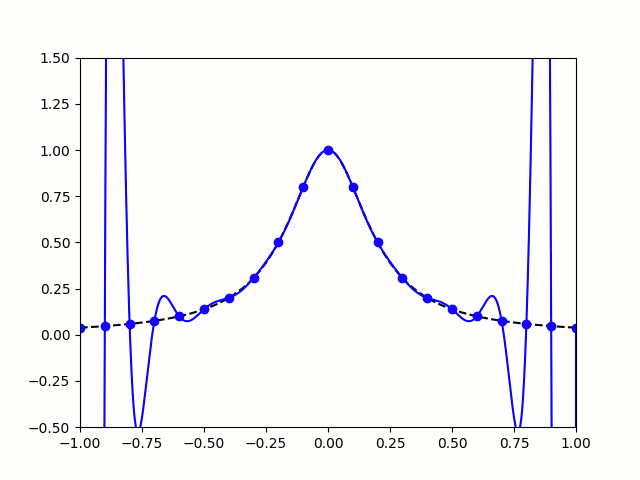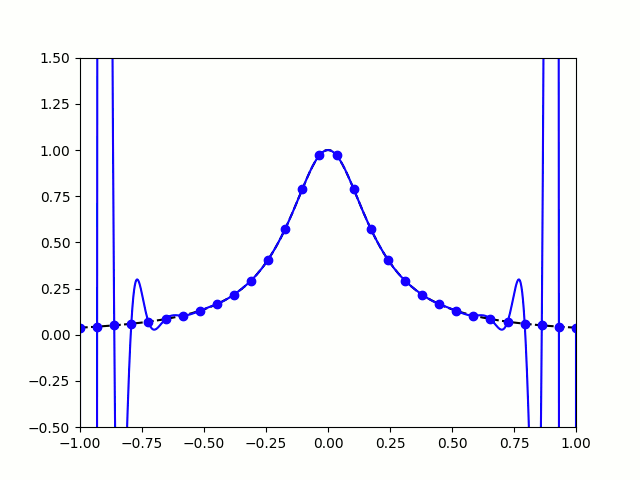
考虑到 M M M是稀疏带状矩阵,可以通过LU分解的方式以线性时间复杂度求解 M P = D \boldsymbol{M} \boldsymbol{P}=\boldsymbol{D} MP=D,而无需进行 O ( N 2 ) O\left(N^{2}\right) O(N2) 复杂度的矩阵求逆。需要注意,时间微分约束的阶次越高,多项式轨迹的次数越高,可能造成函数解析区间过小,产生插值两端剧烈振荡的龙格现象(runge phenomenon)。
3 算法仿真
3.1 C++实现
为了可以通用地支持不同维度、边界阶数与中间阶数的BIVP问题求解,我设计了下面的求解器模板类
cpp
template <typename problem_type>
struct ProblemTraits
{
// 1. problem dimension
// 2. boundary_order
// 3. intermediate_order
};
template <typename problem_type>
class BIVPSolver
{
public:
using Traits = ProblemTraits<problem_type>;
static constexpr size_t boundary_order = Traits::boundary_order;
static constexpr size_t intermediate_order = Traits::intermediate_order;
static_assert(intermediate_order <= boundary_order, "intermediate_order cannot exceed boundary_order");
using BoundaryState = Eigen::Matrix<double, boundary_order + 1, Traits::problem_dim>;
using IntermediateState = Eigen::Matrix<double, intermediate_order + 1, Traits::problem_dim>;
using IntermediateStates = std::vector<IntermediateState>;
}通过ProblemTraits结构体参数化问题特性,将问题维度、边界阶数和中间阶数抽象为类型成员,使求解器能灵活适配车辆二维、无人机四维等不同维度问题场景,以及不同维度最小控制问题的工程需求。利用Eigen矩阵的高效运算能力以及模板编译器推导的特性,可以使求解计算效率达到落地的需求。
接下来看一个使用案例,以二维路径平滑问题为例实例化一个求解器
cpp
struct WaypointProblem
{
static constexpr size_t problem_dim = 2; // x, y
static constexpr size_t boundary_order = 2; // position, velocity, accleration
static constexpr size_t intermediate_order = 0; // position
};
template <>
struct rmp::common::math::ProblemTraits<WaypointProblem>
{
static constexpr size_t problem_dim = WaypointProblem::problem_dim;
static constexpr size_t boundary_order = WaypointProblem::boundary_order;
static constexpr size_t intermediate_order = WaypointProblem::intermediate_order;
};
using Solver = rmp::common::math::BIVPSolver<WaypointProblem>;设置以下的测试用例
cpp
std::vector<std::pair<double, double>> waypoints = {
{ 0.0, 0.0 }, { 4.0, 2.0 }, { 9.0, 0.5 }, { 5.5, -1.0 }, { 10.0, -4.0 }
};
Solver solver;
Solver::BoundaryState start_boundary, end_boundary;
start_boundary.setZero();
end_boundary.setZero();
start_boundary(0, 0) = waypoints[0].first;
start_boundary(0, 1) = waypoints[0].second;
start_boundary(1, 0) = 0.0;
start_boundary(1, 1) = 0.0;
start_boundary(2, 0) = 0.0;
start_boundary(2, 1) = 0.0;
end_boundary(0, 0) = waypoints.back().first;
end_boundary(0, 1) = waypoints.back().second;
end_boundary(1, 0) = 0.0;
end_boundary(1, 1) = 0.0;
end_boundary(2, 0) = 0.0;
end_boundary(2, 1) = 0.0;
solver.setBoundaryConstraints(start_boundary, end_boundary);
Solver::IntermediateStates intermediate_constraints;
for (size_t i = 1; i < waypoints.size() - 1; ++i)
{
Solver::IntermediateState constraint;
constraint.setZero();
constraint(0, 0) = waypoints[i].first;
constraint(0, 1) = waypoints[i].second;
intermediate_constraints.push_back(constraint);
}
solver.setIntermediateConstraints(intermediate_constraints);
double dt = 10.0;
std::vector<double> time_allocation;
double total_time = 0.0;
for (size_t i = 0; i < waypoints.size() - 1; ++i)
{
time_allocation.push_back(dt);
total_time += dt;
}
solver.setTimeAllocation(time_allocation);
Eigen::MatrixXd solution = solver.solve();得到以下的优化结果
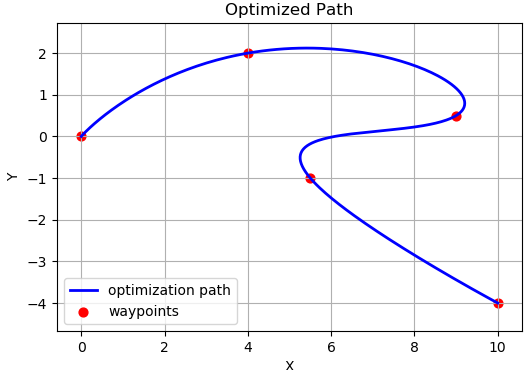
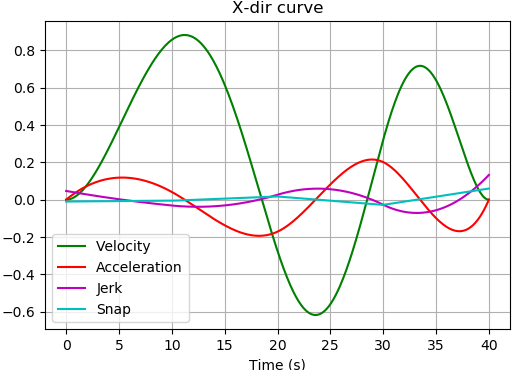
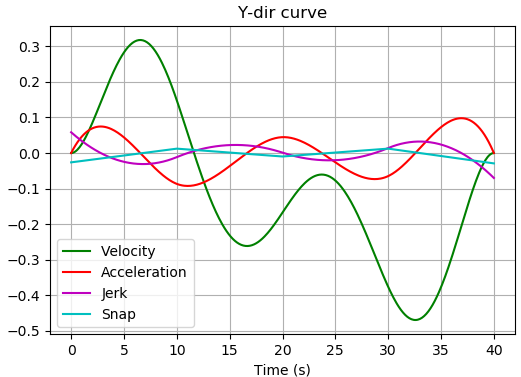
3.2 Python仿真
核心代码如下所示
python
def solve(self):
if not self.is_boundary_constraint_set:
raise RuntimeError(f"No valid boundary constraints.")
if not self.is_intermediate_constraint_set:
raise RuntimeError(f"No valid intermediate constraints.")
s = self.params.boundary_constraint_order + 1
ri = self.params.intermediate_constraint_order + 1
ri_bar = 2 * s - ri
M = np.zeros((s * self.segments_num * 2, s * self.segments_num * 2))
D = np.zeros((s * self.segments_num * 2, self.params.problem_dim))
# initial boundary
for r in range(s):
M[r, 0 : 2 * s] = self.beta(0, r)
D[r, :] = self.D0[r, :]
# intermediate boundary
for seg in range(self.segments_num - 1):
start_row_index = s + 2 * s * seg
start_col_index = 2 * s * seg
for r in range(ri):
M[start_row_index + r, start_col_index : start_col_index + 2 * s] = self.beta(
self.time_allocation[seg], r
)
D[start_row_index + r, :] = self.Di[seg][r, :]
start_row_index += ri
for r in range(ri_bar):
M[start_row_index + r, start_col_index : start_col_index + 2 * s] = self.beta(
self.time_allocation[seg], r
)
M[
start_row_index + r,
start_col_index + 2 * s : start_col_index + 4 * s,
] = -self.beta(0, r)
# terminal boundary
start_row_index = (self.segments_num - 1) * s * 2 + s
for r in range(s):
M[start_row_index + r, (self.segments_num - 1) * s * 2 :] = self.beta(self.time_allocation[-1], r)
D[start_row_index + r, :] = self.Dk[r, :]
return np.linalg.inv(M) @ D完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇