一、LORA
1.LORA （Low-Rank Adaptation）低秩适配矩阵的来由
现在开源的预训练大语言模型有很多，其预训练任务也在不断的探索中出现了多种方式，但是预训练大语言模型和下游任务之间依然还是有差距（gap），所以在我们使用预训练模型来做任务的时候要么让下游任务的数据格式遵循预训练数据的格式，要么对预训练模型做微调--让模型适配下游任务。
在考量对预训练模型做微调的时候，最暴力的方式就是用人工重新标注后的高质量数据对模型直接开始训练（全量微调），也就是让模型在已经学习到通用知识的情况下在我给的领域数据做深入学习，这个方式带来的最大的问题就是资源的限制 和模型灾难性遗忘。
资源限制：大模型的参数量大，意味着模型训练需要更多的算力资源和时间成本，对于很多公司是不友好的。
模型灾难性遗忘：如果你以为的人工标注的"高质量数据"对于模型而言并不是高质量数据，比如数据量不够大、噪声多、数据的多样化有限等等，都对模型训练后的质量有很大的影响，最坏的情况也就是模型的通用能力被遗忘，有种肉包子打狗一去不复返的蓝廋。
话说回来，也就是我对模型做出改变的时候希望能保住模型在大规模通用语料上学习到的知识和能力，同时也能让模型学习到我想做的任务的偏向性，这个时候就提出了LORA这种参数高效（PEFT）的微调大语言模型方法。
LoRA冻结了预训练的模型权重（保住大模型的通用能力），并将可训练的秩分解矩阵注入到 Transformer 架构的每一层中（学习下游任务的偏向性的知识），从而大大减少了下游任务的可训练参数数量。
2.LORA的图解
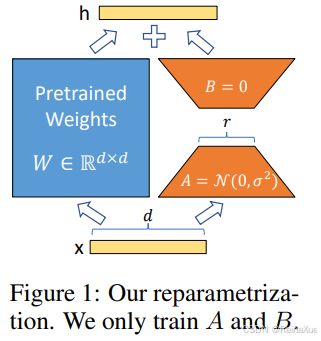论文中的LORA原理图解
【这里我进行简化的理解，不做严谨的数学推导。】
x是输入信息，d是映射空间的维度大小，W是预训练模型的权，A矩阵（d，r），B矩阵（r，d），正态分布初始化A矩阵，全零初始化B矩阵，x经过W和AB矩阵后，得到输出
【这里是我在LORA论文中对于图解的描述的截图，这里产生了一种困惑 --> 因为给到的公式是，B是降维矩阵（将d映射到r维度），也说的是B初始化为0，但是图解中的B是升维矩阵（将r映射回d维度），这里到底是指代降维矩阵初始化为0还是升维矩阵初始化为0产生了困惑，后面参考官方给出的代码，以及便于理解，我这里描述的公式
】
3.为什么
可以用低秩矩阵代替?
ΔW其实是可以通过线性变换被AB矩阵表示，矩阵的秩r表示其列空间（或行空间）的维度，也可以理解为矩阵所包含的线性独立信息量的多少（最大线性无关组）。我们可以通过保留最大的几个奇异值及其对应的奇异向量来近似 原始矩阵，从而实现数据降维或压缩，这正是 LoRA 等低秩适应方法的基础。
用大白话讲，就是大语言模型ΔW从行变换的角度来说有一些行可以被其他行（线性）表示，那么就意味着这些行的信息是重复的（对于更新的信息而言就是无用的），所以我们只需要保留所有不能被其他行表示的行假设有r个，这个r就是矩阵的秩，也是有效信息的数量，其中
。
在计算参数量上的优化：
4.矩阵A和矩阵B怎么初始化?
矩阵A：降维矩阵，从高维度d映射到低维度r，只针对有效信息进行学习
矩阵B：升维矩阵，从低维度r映射到高维度d，保证权重做线性变换后的维度不变
对矩阵A 进行随机高斯 初始化，对矩阵B 进行全零初始化
方面一：
在训练模型的时候，初始状态想要从预训练模型的通用能力开始，也就是LoRA 在微调开始时等价于原始预训练模型，避免了初始偏差，能加速学习。
方面二：
如果只需要满足，那么A=0 或者 B=0 或者 A=B=0也可以实现，但是这里最优的方法是A矩阵随机初始化，B矩阵为0，是梯度流的原因。
正向传播的时候，数据流先通过降维矩阵A，如果降维矩阵A为0，那么升维矩阵B的输入就没有信息，意味着信息被截断 ，反向传播由公式可以看到B无法更新，A被无效更新，这就出现梯度断层，模型表达能力下降。
而如果B为0，在正向传播的时候经过A后，数据是有方向的进行映射，虽然B矩阵为0，在经过B矩阵后的数据存在较大误差，但是在反向传播的时候会缩小误差。由公式可以知道，在反向传播的时候A会保持稳定，B会基于损失进行梯度更新。
如果A=0且B=0，那明显对于模型训练是无意义的。
综上所述，降维矩阵A用随机正太分布初始化，升维矩阵B用全零初始化是最合适的。【当然，实验才是最权威的，论文中也说明了经过大量的实验验证，这样做初始化是最优的】
5.为什么要乘缩放因子?
乘上缩放因子的主要原因是为了 控制 LoRA 模块对预训练模型输出的扰动程度，并稳定训练过程。
-
保持更新幅度的稳定性： 在全量微调中，我们通常会选择一个合适的学习率来更新所有参数。LoRA 引入的低秩更新是一种"增量"更新。如果不进行缩放，随着 r 的增大，ΔW 可能产生更大的扰动，这可能需要更小的主学习率来稳定训练。通过引入 α/r，LoRA 可以使得 LoRA 模块的有效更新幅度在不同 r 值下更具可预测性。
-
解耦 LoRA 学习率与主学习率： 通过 α，我们可以独立地调整 LoRA 模块的"学习强度"，而不需要直接修改优化器的主学习率。这在实践中非常方便，因为主学习率通常是针对整个模型（包括预训练权重和 LoRA 权重）优化的。通过调整 α，我们可以精细地控制 LoRA 模块的贡献，而无需担心破坏主学习率的稳定效果。
-
防止梯度爆炸或消失： 类似于点积注意力中的缩放，这个 缩放因子也有助于 保持 LoRA 模块产生的增量梯度的规模适中，从而避免训练过程中的数值不稳定问题（如梯度爆炸或消失）。
-
实验优化结果： 从实验角度看，论文作者通过大量的实验发现，添加这个 α/r 缩放因子能让 LoRA 在各种任务和模型上表现得更好，并且更容易调优。它使得 LoRA 成为一个更加鲁棒和高效的微调方法。
6.为什么将缩放因子设计为α/r？
这个缩放因子 α/r 的引入，主要是为了在微调 LoRA 模块时，能够以一个稳定的学习率来训练，并且 允许 LoRA 模块的学习率与优化器的主学习率解耦。
-
r (秩) ：如前所述， LoRA 通过引入低秩矩阵 A 和 B 来模拟权重更新 ΔW，其中 r 是这个低秩分解的维度。r 决定了 LoRA 模块的参数量和表达能力。 r 越大，LoRA 模块能够学习到的信息越多，越接近全量微调，但参数量也越大。
-
α (缩放参数) ：α 是 LoRA 引入的一个额外的超参数，它允许我们 调整 LoRA 模块的有效学习率或贡献度 。它的作用可以理解为 "强度" 或者 "学习率补偿"。
当 r 增大时，LoRA 模块的参数量增加，理论上它可以学习到更多的信息。如果 α 保持不变，那么 就会减小。这有助于 抵消 r 增大可能导致的有效更新幅度过大的问题，使得在不同 r 值下，LoRA 模块能够以相对稳定的"步长"进行学习。
论文作者发现，将 α 设置为 2r 或 4r （通常将 α 设置为与 r 相关的常数，比如 α=2r），可以使得在不同 r 值下，模型的性能表现相似，而不需要为每个 r 值单独调整学习率。这表明 α 有助于归一化 LoRA 模块的贡献，使得其对最终模型输出的影响在不同 r 值下保持相对一致。