当自回归模型遇上扩散模型：下一代序列预测模型详解与Pytorch实现

今天我们来详细讲解一下用于序列预测的自回归扩散模型 (Autoregressive Diffusion Models)。

这个模型结合了两种强大思想：自回归 (Autoregressive, AR) 和 扩散模型 (Diffusion Models, DM)，旨在生成高质量、连贯的序列数据。

为了完全理解它，我们先分别解析这两个核心概念，然后再将它们组合起来。

核心概念回顾

1. 扩散模型 (Diffusion Models) 的核心思想

现在我们有一张清晰的图片（代表一个数据点，比如序列中的一个元素）。

前向过程 (Forward Process / Noising): 你不断地、逐步地向这张图片中添加少量的高斯噪声。经过成百上千步之后，这张清晰的图片最终会变成一张完全是随机噪声的图片，原始信息荡然无存。这个过程是固定的、不可学习的。

反向过程 (Reverse Process / Denoising): 扩散模型的核心任务是学习如何"逆转"这个过程。它训练一个深度神经网络（通常是 U-Net 结构），让它学会从一张充满噪声的图片中，预测出上一步添加的噪声是什么。通过一步步地减去预测出的噪声，模型就能从纯粹的随机噪声出发，逐渐"去噪"，最终"创造"出一个清晰、真实的数据点。

关键点： 扩散模型非常擅长生成高质量、细节丰富的数据，因为它将一个复杂的生成任务分解成了许多个简单的去噪小任务。

优点​：

强大的建模能力​：能生成非常高质量和多样化的样本（如图像、音频）。

并行去噪 ​：在反向过程的每一步，可以并行预测所有位置的去噪结果，更好地捕捉序列的全局结构和长期依赖关系。

缺点​：

采样速度慢​：通常需要几十甚至上百步的去噪迭代才能生成一个样本。

2. 自回归模型 (Autoregressive Models) 的核心思想

自回归模型是序列生成的经典方法，其思想非常直观：逐个生成序列中的元素，并且生成当前元素时，要依赖于所有已经生成的历史元素。

最典型的例子就是语言模型（如 GPT）：

• 要生成句子 "The cat sat on the mat."

• 首先生成 "The"。

• 然后基于 "The"，生成 "cat"。

• 然后基于 "The cat"，生成 "sat"。

• ...依此类推。

数学上可以表示为：

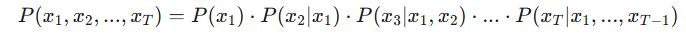
将序列生成看作一个顺序过程。给定之前的所有元素（x₁, x₂, ..., x_{t-1}），预测下一个元素 x_t。这就像逐个单词地写一篇文章。

自回归模型天然地捕捉了序列数据中的时间依赖性和因果关系，保证了生成序列的连贯性。

自回归扩散模型 (AR-DM)

自回归扩散模型的核心思想是 ​：​用扩散模型来代替自回归模型中的"下一个 token 预测器"​。

利用自回归的框架，逐个生成序列的未来元素；而在生成每一个元素时，使用强大的扩散模型来保证其高质量和真实性。

换句话说，传统的自回归模型预测的是 x_t的具体值（或分类分布），而自回归扩散模型预测的是 x_t的整个概率分布，并使用扩散过程来从该分布中采样。

工作原理:

假设我们有一个历史序列

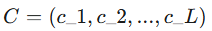（例如过去一周的股票价格）

我们的目标是预测未来的序列

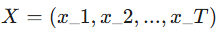（例如未来三天的股票价格）。

AR-DM 的生成过程如下：

1.条件 (Conditioning) ： 模型将已知的历史序列 C作为条件信息。这是自回归思想的体现。

2.初始化噪声 (Initialization) ： 为了生成 x_{t}，我们不是直接预测一个值，而是从一个标准的高斯噪声 z 开始。这个噪声 z 是 x_{t} 的一个"混沌"的初始状态。

3.迭代去噪 (Iterative Denoising) ： 接下来，启动扩散模型的反向去噪过程。在每一步去噪时，去噪网络不仅接收当前的噪声数据z_k**(** 原始数据在添加了 k步噪声后的一个噪声版本**)** ，还同时接收我们给定的条件信息 ，也就是历史序列 C

去噪网络的目标是预测噪声，但它的预测会受到历史序列的影响。例如，如果历史数据显示上升趋势，网络在去噪时就会倾向于生成一个比序列最后一个值更大的值。

这个过程会迭代很多次（比如几十到几百次），z 从纯粹的噪声逐渐变得清晰，最终收敛成一个具体、高质量的预测值 x_{t}。

4.序列扩展与循环 (Append and Repeat)：

当 x_{t+1} 生成后，我们将它拼接到历史序列的末尾，得到新的序列 (x_1, x_2, ..., x_t, x_{t+1})。

如果需要预测 x_{t+2}，就重复上述步骤，把这个新的、更长的序列作为新的条件信息。

在序列预测中的应用与优缺点

自回归扩散模型可以广泛应用于各种序列预测任务：

• 时间序列预测：如股票价格、天气预报、能源负荷预测。历史数据是条件，模型生成未来的数据点。

• 音乐生成：根据已有的旋律片段，生成下一段音乐。

• 文本生成：虽然在文本领域应用不如 Transformer 直接，但其思想也被借鉴于生成更具多样性和创造性的文本。

• 语音合成：生成高质量的语音波形，例如 Google 的 WaveGrad 就是一个经典的例子。

优点

1. 极高的生成质量：继承了扩散模型的优点，生成的序列（无论是数值、音频波形还是其他形式）细节丰富，分布更接近真实数据。

2. 强大的上下文建模能力：自回归的框架保证了模型能够充分利用历史信息，确保了序列的连贯性和逻辑性。

3. 概率性预测：扩散模型本质上是概率生成模型，因此它不仅能给出一个预测值，还能提供预测的置信区间或多种可能的未来路径，这对于风险评估等场景非常重要。

缺点

1. 极慢的生成速度：这是它最大的短板。它叠加了两种"慢"模型的缺点：

   • 自回归：必须串行生成，一个接一个。

   • 扩散模型：生成每一个元素都需要多步迭代去噪。 这导致生成一个长序列非常耗时，限制了其在实时应用中的部署。

2. 模型复杂性高：训练和实现这样一个模型比单纯的 RNN 或 Transformer 要复杂得多。

3. 误差累积：和所有自回归模型一样，如果在某一步生成了有偏差的值，这个错误会被带入到后续的预测中，可能导致误差不断放大。

总结

自回归扩散模型是一种强大而前沿的序列生成技术。它通过将扩散模型的高保真生成能力 与自回归模型的强大序列依赖建模能力相结合，在多个领域展现出了超越传统方法的潜力，尤其擅长生成高质量、高真实感的序列数据。

然而，其巨大的计算开销（特别是推理速度）是目前限制其广泛应用的主要障碍。未来的研究方向很可能会集中在如何加速其生成过程（例如通过知识蒸馏、减少去噪步数等）上。

Pytorch代码实现

由于一个完整的、生产级别的实现会非常复杂，这里我提供一个核心思想和骨架代码 的讲解。这个示例将聚焦于一个简单的一维时间序列预测任务，让大家能够清晰地理解各个组件是如何协同工作的。

我将把实现分解为以下几个关键部分：

1.DiffusionScheduler (扩散过程调度器) ：管理加噪过程中的各种参数（, 等）。

2.DenoisingNetwork (去噪网络)：这是模型的核心，一个神经网络，用于预测每一步的噪声。我们将使用一个基于 Transformer 的结构。

3.AutoregressiveDiffusionModel (主模型)：一个封装类，它将调度器和去噪网络组合起来，并处理自回归的逻辑，负责训练和生成。

第一步：DiffusionScheduler - 管理噪声

这个模块不包含可训练的参数，它的作用是预先计算好扩散过程所需的所有调度变量。

类定义与初始化:

import torch
import torch.nn as nn
import math
class DiffusionScheduler:
    def __init__(self, num_timesteps=1000, beta_start=0.0001, beta_end=0.02):
        self.num_timesteps = num_timesteps
        
        # 1. 定义 beta schedule (噪声方差)
        self.betas = torch.linspace(beta_start, beta_end, num_timesteps)
        
        # 2. 计算 alphas
        self.alphas = 1. - self.betas
        self.alphas_cumprod = torch.cumprod(self.alphas, dim=0) # α_bar
        
        # 3. 计算前向加噪过程所需的其他变量
        self.sqrt_alphas_cumprod = torch.sqrt(self.alphas_cumprod)
        self.sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - self.alphas_cumprod)

扩散模型的前向过程可以用以下概率分布描述：

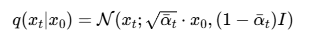
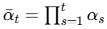
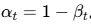
参数说明：

1.num_timesteps： 扩散过程的总时间步数，默认1000步

2**.beta_start** ：噪声方差的起始值，默认0.0001

3.beta_end：噪声方差的结束值，默认0.02

初始化过程：

1.​定义beta计划​：使用torch.linspace创建一个从beta_start到beta_end的线性间隔序列，表示每个时间步的噪声方差

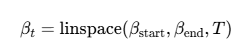
2.​计算alphas​：表示每个时间步保留原始信号的比例

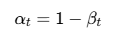
3.计算累积乘积​：表示从开始到时间步t的累积保留比例

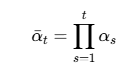
4.​预计算平方根值​：为了后续计算效率，预先计算

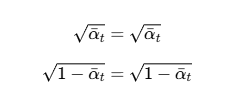
add_noise 方法：

def add_noise(self, original_data, timesteps):
    """
    对原始数据 x_0 添加噪声，得到任意时刻 t 的 x_t
    :param original_data: 干净的数据 x_0, shape [batch_size, seq_len, features]
    :param timesteps: 随机采样的时间步 t, shape [batch_size]
    """
    # 随机采样噪声
    noise = torch.randn_like(original_data)
    
    # 根据公式 x_t = sqrt(α_bar_t) * x_0 + sqrt(1 - α_bar_t) * ε
    # 获取对应时间步 t 的 sqrt(α_bar_t) 和 sqrt(1 - α_bar_t)
    # 需要 unsqueeze 来匹配 original_data 的维度以便广播
    sqrt_alpha_t = self.sqrt_alphas_cumprod[timesteps].view(-1, 1, 1)
    sqrt_one_minus_alpha_t = self.sqrt_one_minus_alphas_cumprod[timesteps].view(-1, 1, 1)
    
    # 计算带噪数据
    noisy_data = sqrt_alpha_t * original_data + sqrt_one_minus_alpha_t * noise
    
    return noisy_data, noise

方法功能：

该方法实现了扩散模型的前向过程，根据公式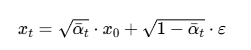对原始数据添加噪声。

其中 ε∼N(0,I)是从标准正态分布采样的噪声。

参数说明：

original_data ：原始干净数据 x_0，形状为 [batch_size, seq_len, features]

timesteps ：随机采样的时间步 t，形状为 [batch_size]

实现细节：

1.从标准正态分布中采样与原始数据形状相同的噪声 ε

2.通过索引获取对应时间步的 √(α_bar_t) 和 √(1-α_bar_t) 值

3.使用.view(-1, 1, 1)调整维度以便进行广播运算

4.按照扩散公式计算带噪声的数据 x_t

5.返回带噪数据和添加的噪声（后者在训练去噪网络时会用到）

第二步：DenoisingNetwork - 预测噪声的核心

这是模型的大脑。对于序列数据，Transformer 是一个非常好的选择。它需要接收三个关键输入：

noisy_x：带噪的当前数据点。

time_emb：扩散时间步 t 的嵌入表示。

context：历史序列的编码表示（自回归的条件）。

我们将使用一个简单的 Transformer Encoder Layer 来实现。

SinusoidalTimeEmbedding 类

这是一个正弦时间嵌入模块，用于将离散的时间步转换为连续的向量表示。

class SinusoidalTimeEmbedding(nn.Module):
    """ Sinusoidal Time Embedding for Diffusion Timesteps """
    def __init__(self, dim):
        super().__init__()
        self.dim = dim

    def forward(self, time):
        device = time.device
        half_dim = self.dim // 2
        embeddings = math.log(10000) / (half_dim - 1)
        embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
        embeddings = time[:, None] * embeddings[None, :]
        embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
        return embeddings

数学原理

正弦位置编码的公式为：

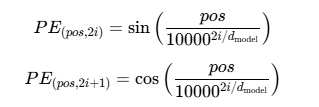
其中：

pos是位置（时间步）

i是维度索引

d model 是嵌入维度

​初始化​：设置嵌入维度

2.​前向传播​：

•计算频率因子：math.log(10000) / (half_dim - 1)

•创建频率向量：torch.exp(torch.arange(half_dim) * -embeddings)

•将时间步与频率向量相乘：time[:, None] * embeddings[None, :]

•分别计算正弦和余弦部分并拼接：torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)

DenoisingNetwork 类

这是一个基于Transformer的去噪网络，用于预测扩散过程中添加的噪声。

网络架构

class DenoisingNetwork(nn.Module):
    def __init__(self, data_dim=1, context_dim=64, time_emb_dim=64, num_layers=4):
        super().__init__()
        
        # 时间步嵌入
        self.time_mlp = nn.Sequential(
            SinusoidalTimeEmbedding(time_emb_dim),
            nn.Linear(time_emb_dim, time_emb_dim),
            nn.ReLU()
        )
        
        # 输入投影，将 (带噪数据 + 时间嵌入 + 上下文) 拼接后映射到模型维度
        self.input_proj = nn.Linear(data_dim + time_emb_dim + context_dim, context_dim)

        # Transformer Encoder 作为核心处理层
        encoder_layer = nn.TransformerEncoderLayer(d_model=context_dim, nhead=4, batch_first=True)
        self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers=num_layers)

        # 输出投影，映射回原始数据维度以预测噪声
        self.output_proj = nn.Linear(context_dim, data_dim)

    def forward(self, noisy_x, timesteps, context):
        """
        :param noisy_x: 带噪数据点 (batch, 1, data_dim)
        :param timesteps: 时间步 (batch,)
        :param context: 历史序列编码 (batch, context_dim)
        """
        # 1. 获取时间嵌入
        time_emb = self.time_mlp(timesteps) # (batch, time_emb_dim)
        
        # 2. 准备拼接
        # unsqueeze context 和 time_emb 以匹配 noisy_x 的序列长度维度 (这里是1)
        context = context.unsqueeze(1) # (batch, 1, context_dim)
        time_emb = time_emb.unsqueeze(1) # (batch, 1, time_emb_dim)
        time_emb = time_emb.repeat(1, noisy_x.shape[1], 1) # (batch, 1, time_emb_dim)

        # 3. 拼接输入
        x = torch.cat([noisy_x, time_emb, context], dim=-1)
        x = self.input_proj(x) # (batch, 1, context_dim)
        
        # 4. 通过 Transformer 处理
        x = self.transformer_encoder(x)
        
        # 5. 预测噪声
        predicted_noise = self.output_proj(x)
        
        return predicted_noise

组件详解

1.​时间嵌入模块​：

•使用正弦位置编码将离散时间步转换为连续向量

•通过线性层和ReLU激活进一步处理时间嵌入

2.​输入投影层​：

•将带噪数据、时间嵌入和上下文信息拼接

•使用线性层将拼接后的特征映射到模型维度

3.​Transformer编码器​：

•使用多层Transformer编码器处理序列数据

•每层包含自注意力机制和前馈网络

4.​输出投影层​：

•将Transformer输出映射回原始数据维度

•预测添加到原始数据中的噪声

前向传播过程

1.将时间步转换为时间嵌入向量

2.调整上下文和时间嵌入的维度以匹配带噪数据

3.拼接所有输入信息

4.通过输入投影层进行特征变换

5.使用Transformer编码器处理序列

6.通过输出投影层预测噪声

这个网络结构是扩散模型中的核心组件，负责根据当前时间步和上下文信息预测需要从带噪数据中移除的噪声。

第三步：AutoregressiveDiffusionModel - 整体封装

这个类将所有部分组合起来，并定义训练 (forward) 和推理 (predict) 的逻辑。

ADM类详解

这是一个自回归扩散模型，结合了扩散模型和时间序列预测的能力，用于生成连续的时间序列数据。

模型架构概述
该模型结合了以下几个核心组件：

1.​扩散调度器​：管理噪声添加和去除的过程

2.​去噪网络​：预测添加到数据中的噪声

3.​上下文编码器​：使用GRU编码历史序列信息

4.​自回归机制​：逐步生成序列中的每个点

训练过程

在训练阶段，模型学习从带噪数据中预测添加的噪声：

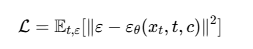
其中：

•ε是实际添加的噪声

•εθ是去噪网络预测的噪声

•xt是时间步 t的带噪数据

•c是历史序列的上下文编码

推理过程

在推理阶段，模型使用DDPM（Denoising Diffusion Probabilistic Models）的采样过程：

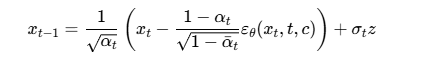
初始化

def __init__(self, data_dim=1, history_len=64, context_dim=64, time_emb_dim=64, num_diffusion_steps=1000):
    super().__init__()
    self.data_dim = data_dim
    self.history_len = history_len
    
    # 1. 实例化组件
    self.scheduler = DiffusionScheduler(num_timesteps=num_diffusion_steps)
    self.denoising_net = DenoisingNetwork(data_dim, context_dim, time_emb_dim)
    
    # 2. 上下文编码器 (这里用一个简单的 GRU 来编码历史序列)
    self.context_encoder = nn.GRU(input_size=data_dim, hidden_size=context_dim, batch_first=True)
    
    # 3. 损失函数
    self.loss_fn = nn.MSELoss()

训练过程 (forward方法)

def forward(self, sequences):
    """
    训练逻辑
    :param sequences: 一个 batch 的序列, shape [batch_size, seq_len, data_dim]
    """
    # 1. 准备数据：从序列中随机采样 历史(context) 和 目标(target)
    history = sequences[:, :self.history_len, :]
    target = sequences[:, self.history_len:self.history_len+1, :] # Shape: [batch, 1, data_dim]

    batch_size = sequences.shape[0]
    device = sequences.device
    
    # 2. 编码历史序列作为上下文
    _, context = self.context_encoder(history)
    context = context.squeeze(0) # [batch, context_dim]
    
    # 3. 随机采样扩散时间步 t
    timesteps = torch.randint(0, self.scheduler.num_timesteps, (batch_size,), device=device).long()
    
    # 4. 为 target 添加噪声
    noisy_target, noise = self.scheduler.add_noise(target, timesteps)
    
    # 5. 使用网络预测噪声
    predicted_noise = self.denoising_net(noisy_target, timesteps, context)
    
    # 6. 计算损失
    loss = self.loss_fn(predicted_noise, noise)
    
    return loss

推理过程 (predict方法)

@torch.no_grad()
def predict(self, history):
    """
    推理/生成逻辑
    :param history: 起始的历史序列, shape [batch_size, history_len, data_dim]
    """
    batch_size = history.shape[0]
    device = history.device
    
    # 1. 编码历史作为上下文
    _, context = self.context_encoder(history)
    context = context.squeeze(0)
    
    # 2. 从纯噪声开始生成新的一个点
    new_point_noisy = torch.randn((batch_size, 1, self.data_dim), device=device)
    
    # 3. 反向去噪循环
    for t in reversed(range(self.scheduler.num_timesteps)):
        timesteps = torch.full((batch_size,), t, device=device, dtype=torch.long)
        
        # 预测噪声
        predicted_noise = self.denoising_net(new_point_noisy, timesteps, context)
        
        # 使用 DDPM 的去噪公式计算上一步的样本
        alpha_t = self.scheduler.alphas[t]
        alpha_t_cumprod = self.scheduler.alphas_cumprod[t]
        beta_t = self.scheduler.betas[t]
        
        coeff1 = 1 / torch.sqrt(alpha_t)
        coeff2 = (1 - alpha_t) / torch.sqrt(1 - alpha_t_cumprod)
        
        new_point_noisy = coeff1 * (new_point_noisy - coeff2 * predicted_noise)
        
        if t > 0:
            noise = torch.randn_like(new_point_noisy)
            variance = torch.sqrt(beta_t) * noise
            new_point_noisy += variance
            
    # 循环结束后，new_point_noisy 就是去噪后的干净数据
    return new_point_noisy

总结与注意事项

• 这是一个简化的骨架 ：真实的实现会更复杂，例如，DenoisingNetwork 会使用更复杂的结构（如交叉注意力来融合上下文），反向采样过程可能会使用更高效的 DDIM 调度器。

• 上下文编码：我们用了一个简单的 GRU，你也可以用 Transformer Encoder 或其他更强大的网络来编码历史信息。

• 训练数据准备 ：在实际应用中，你需要创建一个 Dataset 和 DataLoader，从长时序数据中滑动窗口式地采样出 [batch, history_len + prediction_len, features] 形状的数据块。

• 多步预测 ：要连续预测多个点，你需要在一个循环中调用 predict 方法，并将每次生成的新点添加到历史序列的末尾，再作为下一次预测的输入。

• 参考库 ：如果你想在实际项目中使用，强烈建议参考或直接使用 Hugging Face 的 diffusers 库。它提供了经过严格测试和优化的扩散模型组件，你可以更方便地将它们组合成自回归的形式。