题目链接:
题目描述:
题目解析:
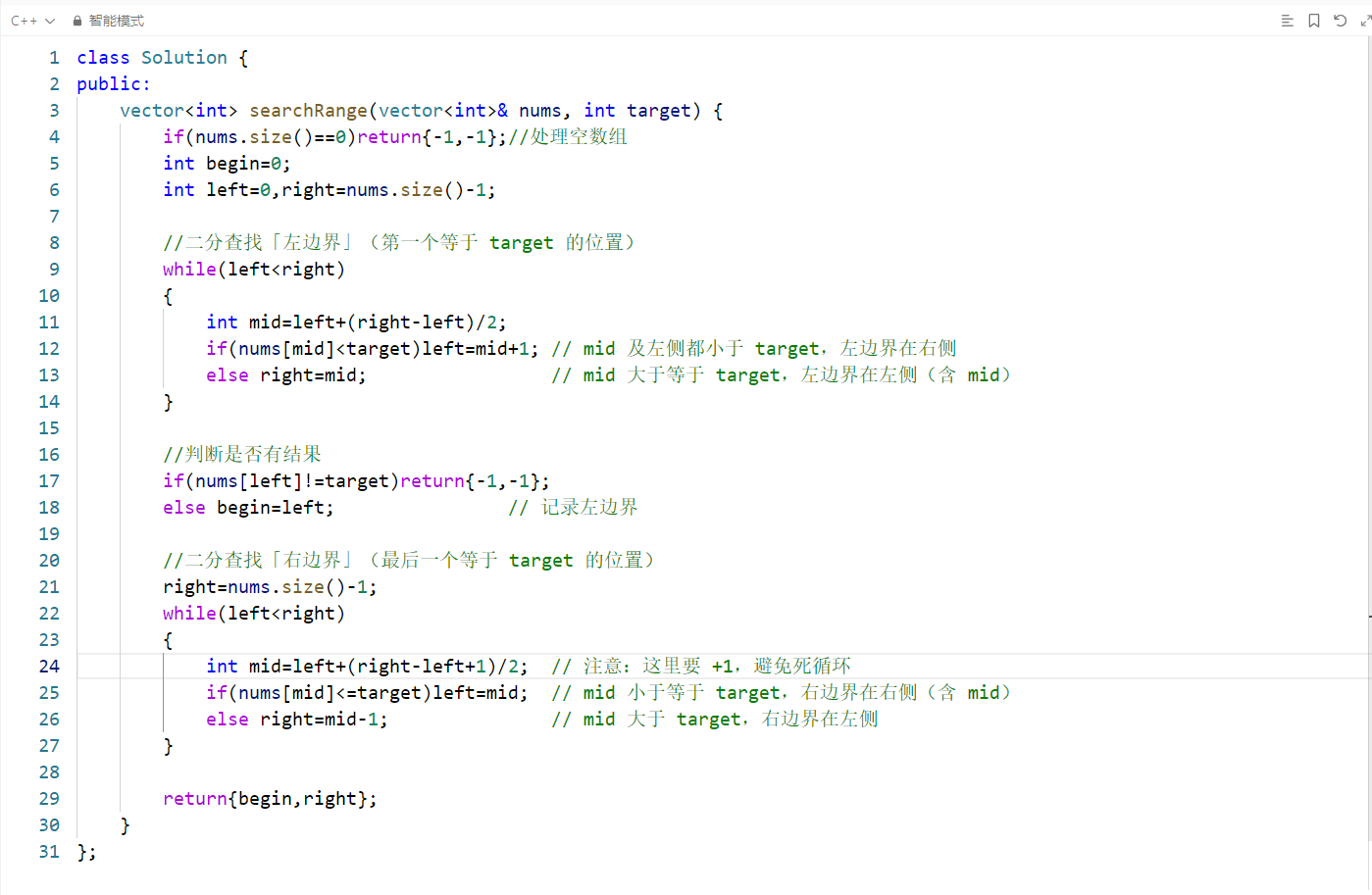
1. 边界判断:处理空数组
- 若数组为空,直接返回
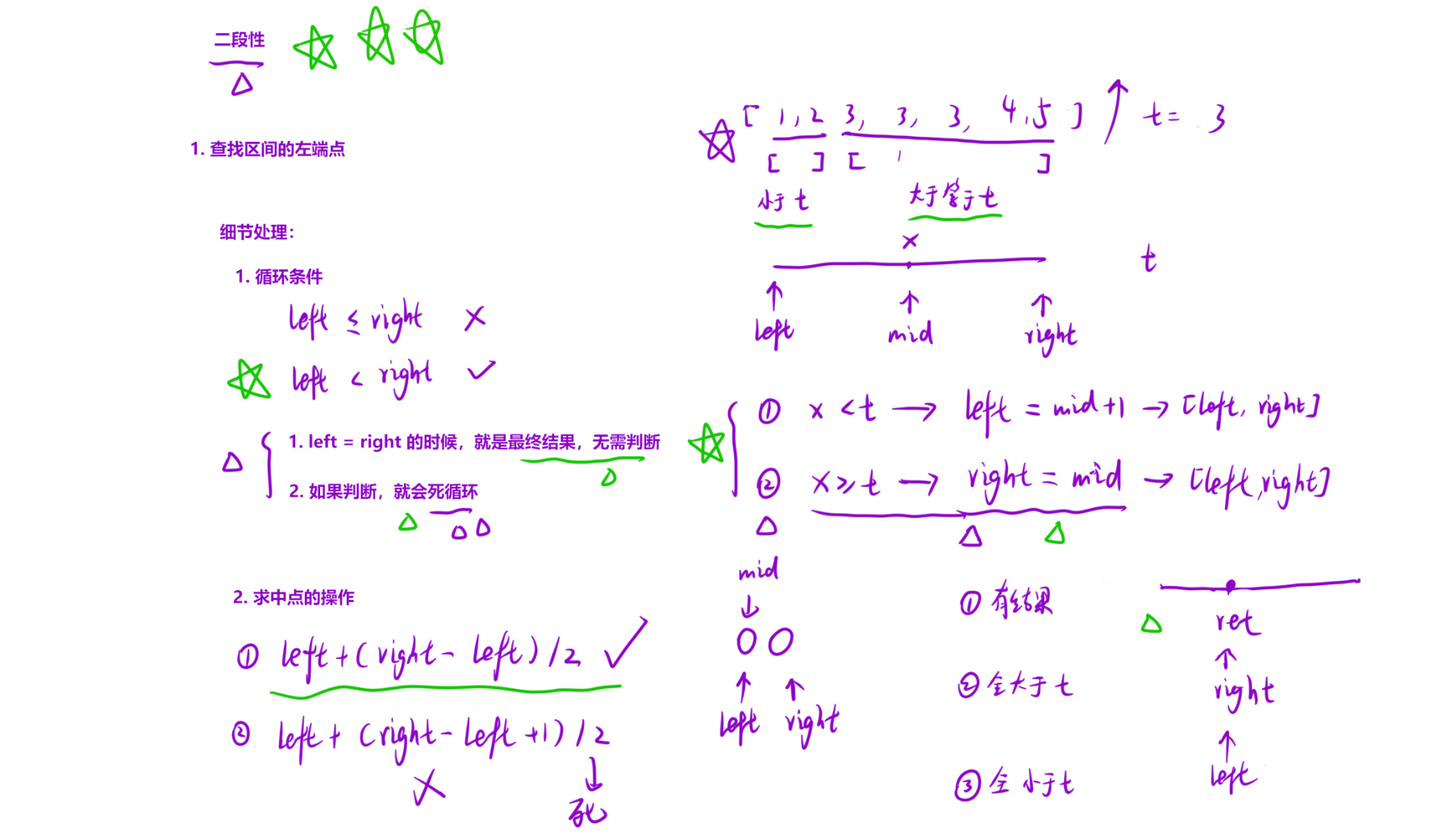
[-1,-1],避免后续索引访问越界。2. 第一步:二分查找「左边界」(第一个等于 target 的位置)
关键逻辑:
通过调整
right的取值(始终指向「可能是左边界」的位置),最终left会收敛到 第一个等于 target 的索引。
- 若
nums[mid] < target:说明 mid 及左边都不可能是左边界,左边界必须在mid+1右侧;- 若
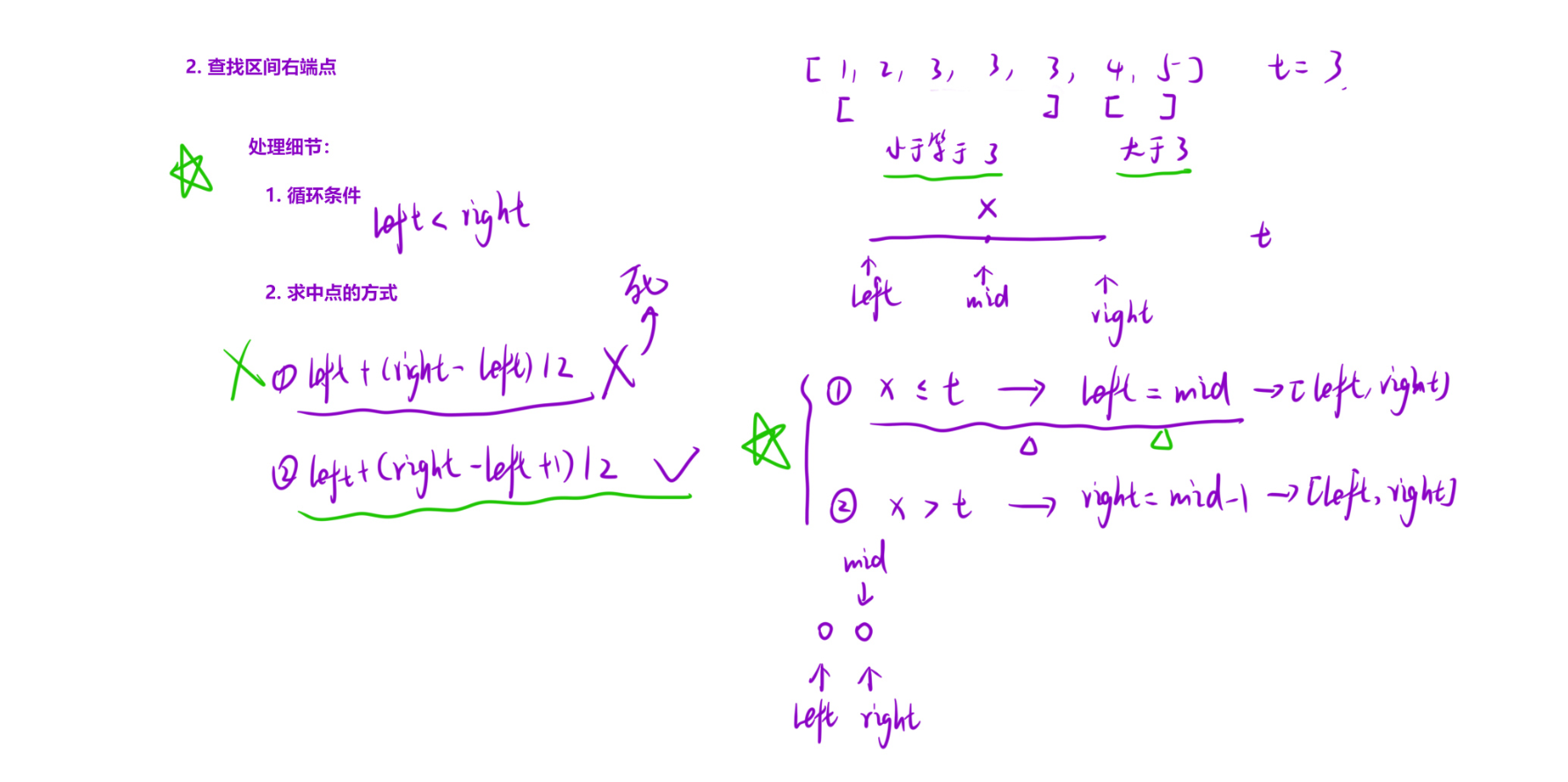
nums[mid] >= target:说明 mid 可能是左边界,或左边界在 mid 左侧,因此将right收缩到 mid。3. 第二步:二分查找「右边界」(最后一个等于 target 的位置)
关键逻辑:
通过调整
left的取值(始终指向「可能是右边界」的位置),最终right会收敛到 最后一个等于 target 的索引。
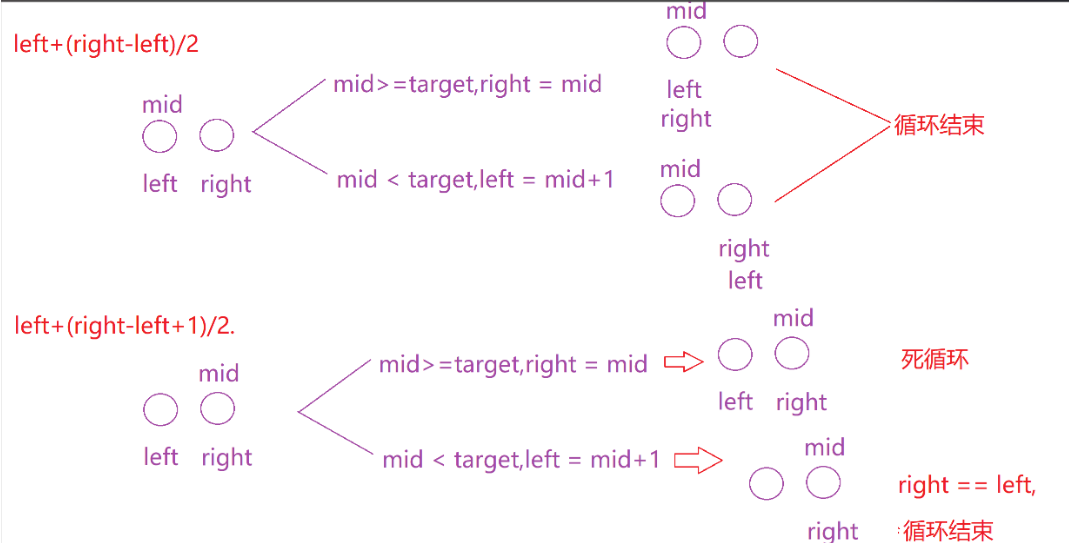
- 为什么要
+1?- 若不
+1,当right = left + 1时,mid = left + (right-left)/2 = left,若nums[mid] <= target,left仍会停在 left,导致无限循环。- 例如:
nums = [8,8],left=0,right=1,不+1时mid=0,nums[mid]<=8则left=0,循环永远不结束;+1后mid=1,nums[mid]<=8则left=1,循环结束。核心优势与注意事项
优势
- 高效性:二分查找的时间复杂度为 O (log n),适合大规模有序数组;
- 鲁棒性:处理了空数组、target 不存在、target 仅出现一次等所有边界情况;
- 无冗余:先找左边界,再基于左边界找右边界,避免重复计算。
注意事项
- 数组必须有序:代码依赖「非递减排序」的前提,若数组无序,需先排序(但排序会改变原索引,失去意义);
- 避免整数溢出 :计算
mid时用left + (right-left)/2而非(left+right)/2,防止left+right超过 int 最大值;- 右边界的 +1 细节 :必须在计算右边界的
mid时加 1,否则会出现死循环。