leetcode 329 矩阵中的最长递增路径

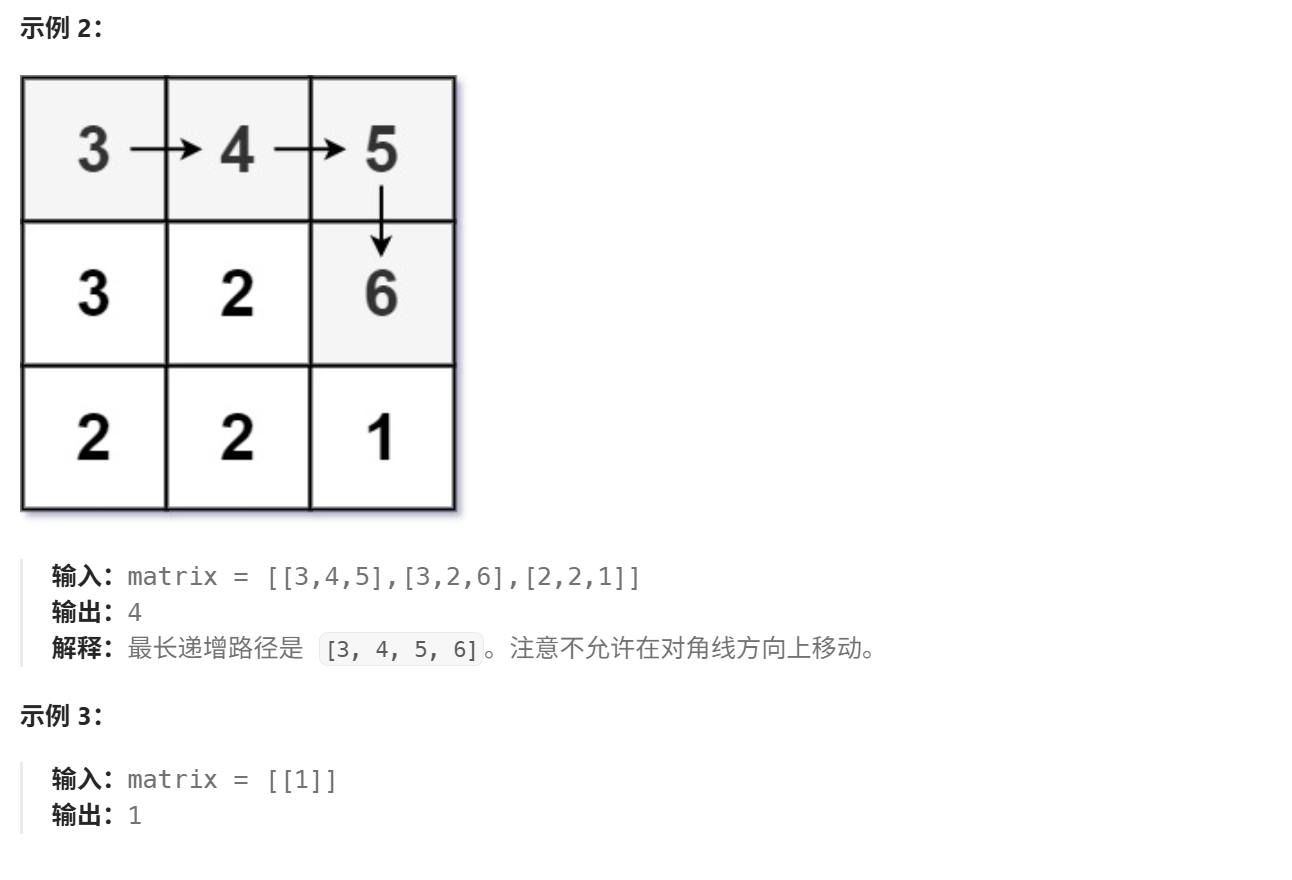
一、问题描述

二、解题思路

解法一：深度优先搜索

（1）整体思路：

可以采用深度优先搜索+剪枝来解决这个问题。遍历matrix数组，对每一个位置进行深度优先搜索，找到以该位置为起点的递增路径的最大长度，遍历完matrix数组后，最长的递增路径的长度即为所求。

（2）函数功能：

dfs函数用于返回以(i，j)为起点的递增路径的最大长度。

（3）dfs函数体：

1>变量longth用于记录递增路径的长度，初始化为1；

2>按照上、右、下、左的顺序从(i，j)位置进行探索，如果matrix $i$ $j$ <matrix $x$ $y$ 且x和y不越界，就就将path更新为max(path,dfs(matrix,x,y)+1)；

3>最后返回path即可；

解法二：记忆化搜索

由于解法一存在大量的重复计算，所以我们可以定义一个数组memo来记录已经计算过的量，memo $i$ $j$ 即为dfs(matrix,i,j)的值：

（1）如果memo $i$ $j$ !=0,就表示这个值已经计算过了，直接返回memo $i$ $j$ ；

（2）如果没有被计算，就进入下面的循环，再在返回path之前更新memo $i$ $j$ ；

三、代码实现

解法一：深度优先搜索(超时)

cpp 复制代码

class Solution {
    int m,n;
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
       //初始化全局变量
       m=matrix.size();
       n=matrix[0].size();

       int ret=0;
       for(int i=0;i!=m;i++)
        for(int j=0;j!=n;j++)
            ret=max(ret,dfs(matrix,i,j));

        return ret;
    }
    int dx[4]={0,1,0,-1};
    int dy[4]={1,0,-1,0};

    int dfs(vector<vector<int>>& matrix,int i,int j){
        int longth=1;
        for(int k=0;k!=4;k++){
            int x=i+dx[k];
            int y=j+dy[k];
            if(x>=0&&x<m&&y>=0&&y<n&&matrix[i][j]<matrix[x][y])
                longth=max(longth,dfs(matrix,x,y)+1);
        }
        return longth;
    }
};

解法二：记忆化搜索(优化)

cpp 复制代码

class Solution {
    int m,n;
    vector<vector<int>> memo;
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
       //初始化全局变量
       m=matrix.size();
       n=matrix[0].size();
       memo.resize(m,vector<int>(n,0));

       int ret=0;
       for(int i=0;i!=m;i++)
        for(int j=0;j!=n;j++)
            ret=max(ret,dfs(matrix,i,j));

        return ret;
    }
    int dx[4]={0,1,0,-1};
    int dy[4]={1,0,-1,0};

    int dfs(vector<vector<int>>& matrix,int i,int j){
        int longth=1;
        if(memo[i][j]!=0) return memo[i][j];

        for(int k=0;k!=4;k++){
            int x=i+dx[k];
            int y=j+dy[k];
            if(x>=0&&x<m&&y>=0&&y<n&&matrix[i][j]<matrix[x][y])
                longth=max(longth,dfs(matrix,x,y)+1);
        }
        memo[i][j]=longth;
        return longth;
    }
};