【机器学习11】决策树进阶、随机森林、XGBoost、模型对比

文章目录

[一决策树的特征处理](#一决策树的特征处理)
- [1.1 处理多值分类特征：独热编码](#1.1 处理多值分类特征：独热编码)
- [1.2 处理连续特征](#1.2 处理连续特征)
[二用于回归任务的决策树](#二用于回归任务的决策树)
- [2.1 回归树的结构与预测](#2.1 回归树的结构与预测)
- [2.2 回归树的分裂标准：方差缩减](#2.2 回归树的分裂标准：方差缩减)
[三集成学习：从决策树到森林](#三集成学习：从决策树到森林)
- [3.1 决策树的敏感性](#3.1 决策树的敏感性)
- [3.2 树集成：群体的智慧](#3.2 树集成：群体的智慧)
- [3.3 Bagging 与随机森林](#3.3 Bagging 与随机森林)
- [3.4 提升法与XGBoost](#3.4 提升法与XGBoost)
[四决策树与神经网络的对比](#四决策树与神经网络的对比)

一决策树的特征处理

在上一篇文章中，我们介绍了决策树的基本概念。现在，我们将探讨决策树如何处理不同类型的特征，包括具有多个值的分类特征和连续值特征。

1.1 处理多值分类特征：独热编码

在之前的例子中，我们的分类特征都只有两个可能的值（例如，"Pointy" vs "Floppy"）。但如果一个特征有三个或更多的可能值呢？例如，上图中的"Ear shape"（耳朵形状）特征现在有三种可能的值："Pointy"（尖耳朵）、"Oval"（椭圆形耳朵）和"Floppy"（软塌耳朵）。

直接使用这种多值特征可能会给某些算法带来问题。一种标准、通用的处理方法是独热编码（One-hot encoding）。其规则是：

如果一个分类特征有 k 个可能的取值，那么就创建 k 个新的二元（binary）特征，每个特征只取0或1。
对于一个样本，其原始特征值对应的那个新特征为1，其余 k-1 个新特征都为0。

如上图所示，"Ear shape"这个特征被转换成了三个新的特征："Pointy ears"、"Floppy ears"和"Oval ears"。

第一行样本的耳朵是"Pointy"，所以在新特征中，"Pointy ears"为1，其余两个为0。
第二行样本的耳朵是"Oval"，所以在新特征中，"Oval ears"为1，其余两个为0。

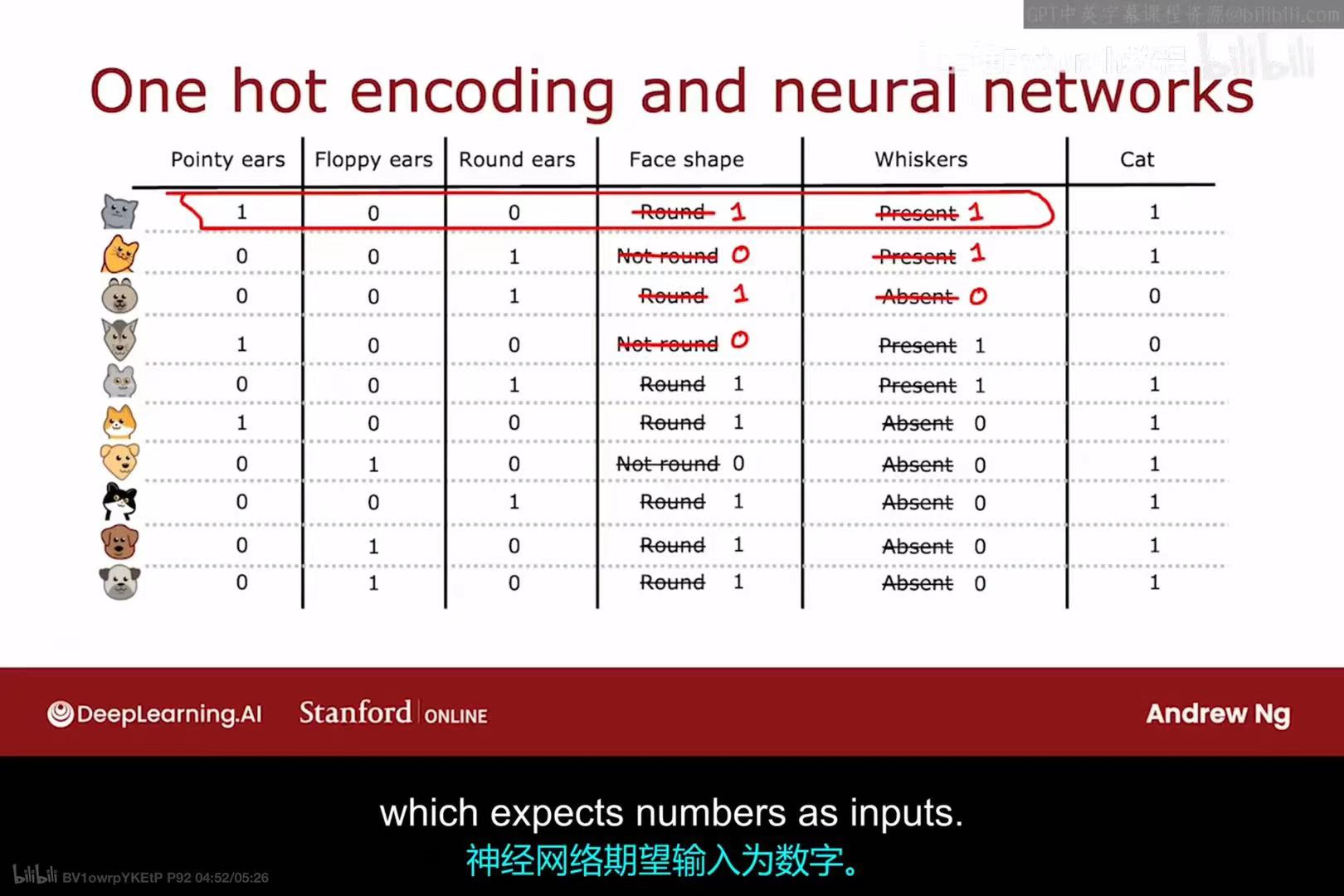
这种将分类数据转换为数值数据的技术不仅适用于决策树，也适用于神经网络等其他多种机器学习模型，因为这些模型通常期望输入是数值形式。通过独热编码，我们可以将所有分类特征（如"Face shape"、"Whiskers"）都转换为0和1的表示，从而形成一个完全由数值组成的输入数据集。

1.2 处理连续特征

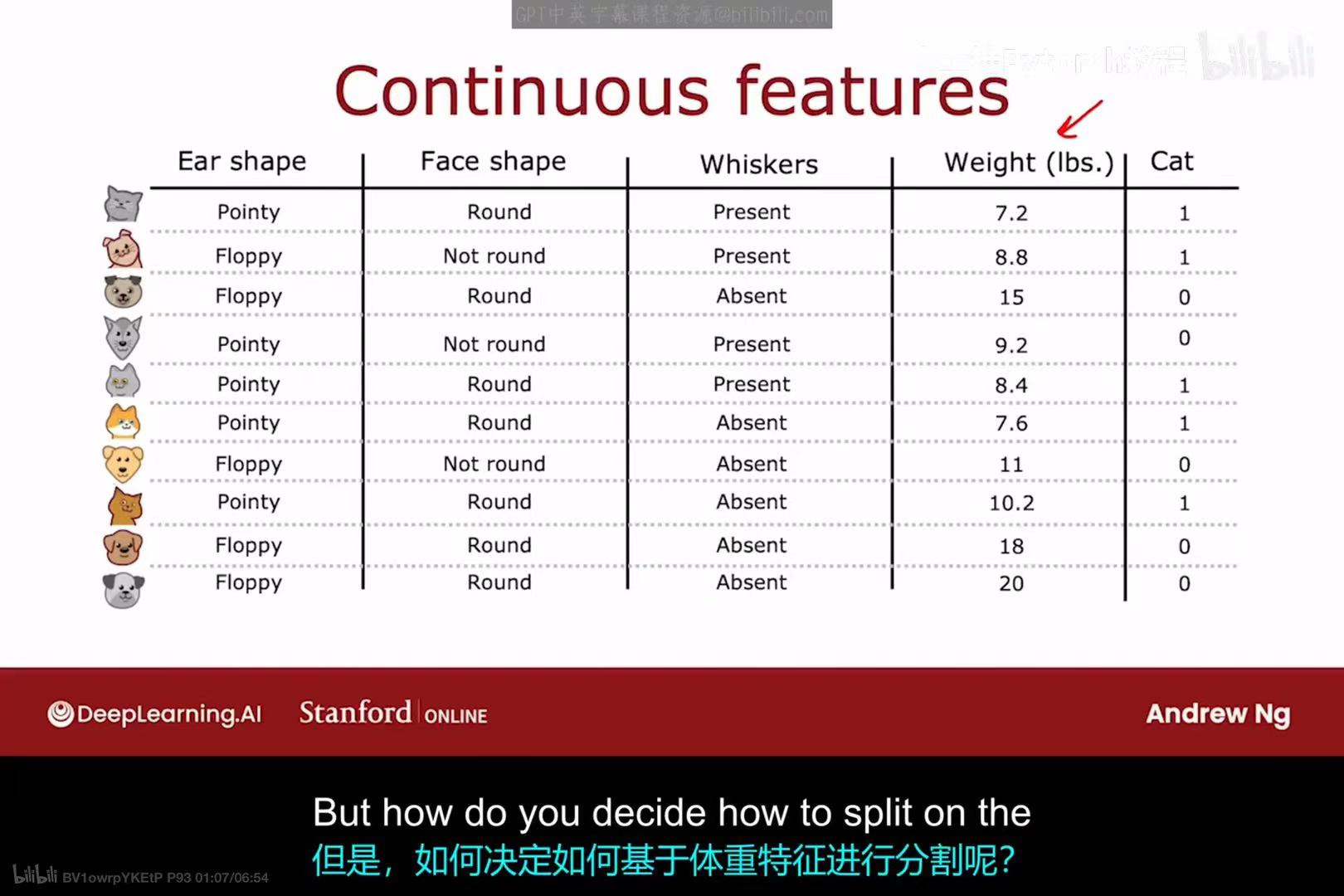
除了分类特征，数据集中也常常包含连续特征（Continuous features），例如上图中新增的"Weight (lbs.)"（体重，单位为磅）。决策树同样可以处理这类特征。

对于一个连续特征，决策树需要决定一个分割点（split point），将其转换为一个二元判断。例如，对于体重特征，一个可能的分割是"Weight <= 9 lbs."。

决策过程：算法会尝试所有可能的分割点。通常，这些分割点会选择在两个相邻数据点的中间位置。
选择标准 ：对于每一个尝试的分割点，算法都会像处理分类特征一样，计算其信息增益。
最终，算法会选择那个能够提供最高信息增益的分割点作为这个连续特征的最佳分割策略。例如，如果"Weight <= 9"这个分割带来的信息增益高于其他所有可能的分割，也高于其他所有特征，那么它就会被选为当前节点的分裂标准。

二用于回归任务的决策树

决策树不仅能用于分类任务，也能用于回归（Regression任务，即预测一个连续的数值。

2.1 回归树的结构与预测

当我们的目标 y 是一个连续数值（如体重）时，这个问题就从分类问题变成了回归问题。

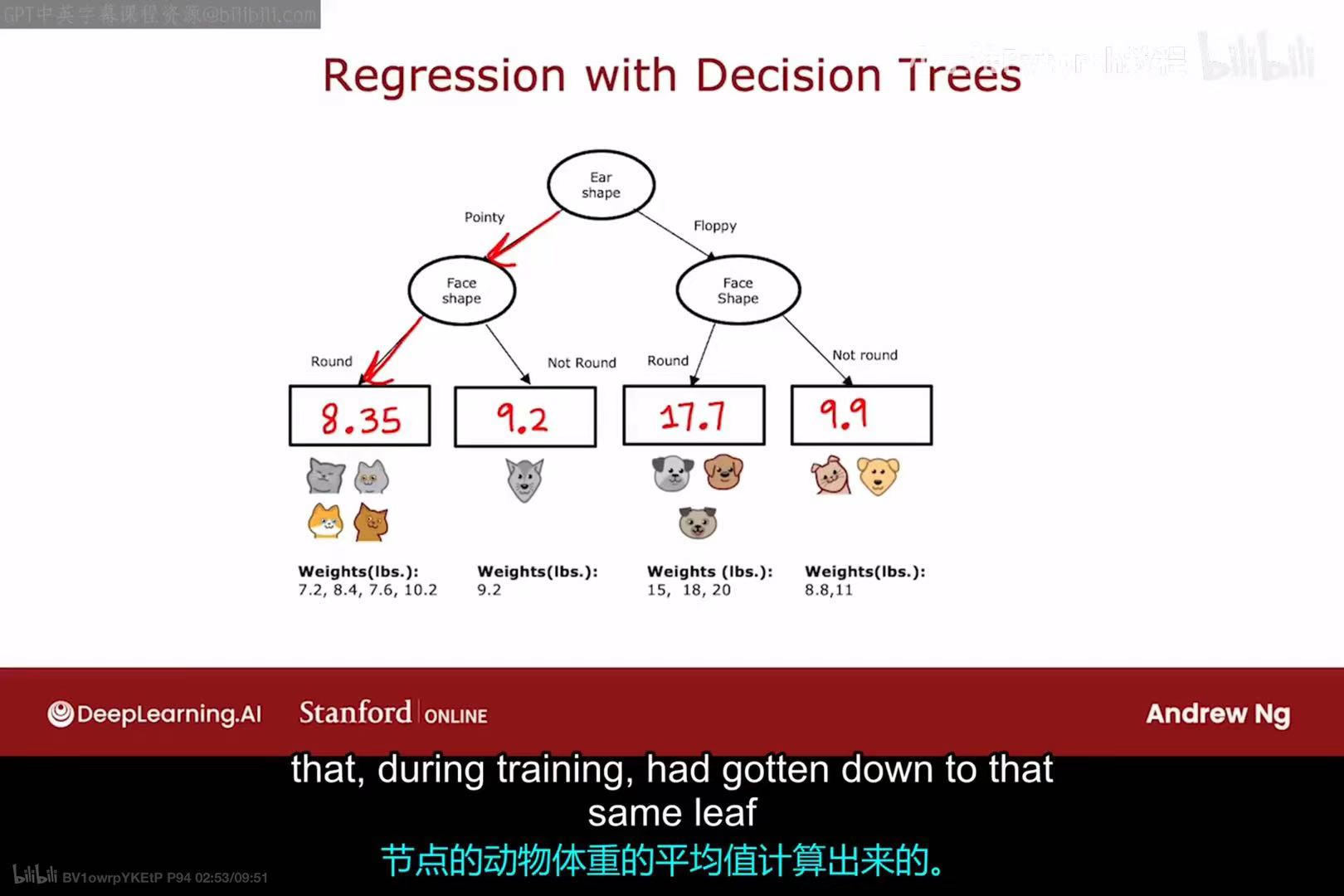
用于回归任务的决策树（简称回归树）的结构与分类树类似，但其叶节点的内容不同：

分类树的叶节点：包含一个类别标签（如"Cat"或"Not cat"）。
回归树的叶节点 ：包含一个具体的数值。
预测方法：一个新样本从根节点开始，沿着树的分支走到某个叶节点，该叶节点中的数值就是模型对这个样本的预测值。
叶节点数值的确定 ：在训练过程中，落入某个叶节点的所有训练样本 ，其目标值 y 的平均值，会被作为这个叶节点的预测值。例如，左下角的叶节点包含4个训练样本，它们的体重分别是7.2, 8.4, 7.6, 10.2，其平均值为8.35，因此该叶节点的预测值就是8.35。

2.2 回归树的分裂标准：方差缩减

对于回归树，我们不再使用基于熵的信息增益来选择最佳分裂特征，因为熵是为分类问题定义的。取而代之，我们使用方差（Variance作为不纯度的衡量标准。

目标：选择一个分裂，使得分裂后各个子节点中目标值 y 的方差尽可能小。
计算过程 ：
1. 计算分裂前父节点中所有样本目标值 y 的方差。
2. 对每个可能的特征和分裂点，计算分裂后子节点方差的加权平均值。
3. 选择那个能使方差缩减（Variance Reduction程度最大的分裂。
在图例中，根节点的方差为20.51。
- 按"Ear shape"分裂，分裂后的加权方差为 (5/10)*1.47 + (5/10)*21.87 = 11.67，方差缩减了 20.51 - 11.67 = 8.84。
- 按"Face Shape"分裂，方差缩减了 0.64。
- 按"Whiskers"分裂，方差缩减了 6.22。
因为"Ear shape"带来的方差缩减最大，所以算法选择它作为根节点的分裂特征。这个过程会递归地进行下去，直到满足停止分裂的条件。

三集成学习：从决策树到森林

3.1 决策树的敏感性

单个决策树有一个显著的缺点：它们对训练数据中的微小变化高度敏感 。如上图所示，仅仅改变一个训练样本的标签（从猫变成狗），就可能导致学习算法构建出一棵结构完全不同的决策树。这种不稳定性是模型高方差（high variance的表现。

3.2 树集成：群体的智慧

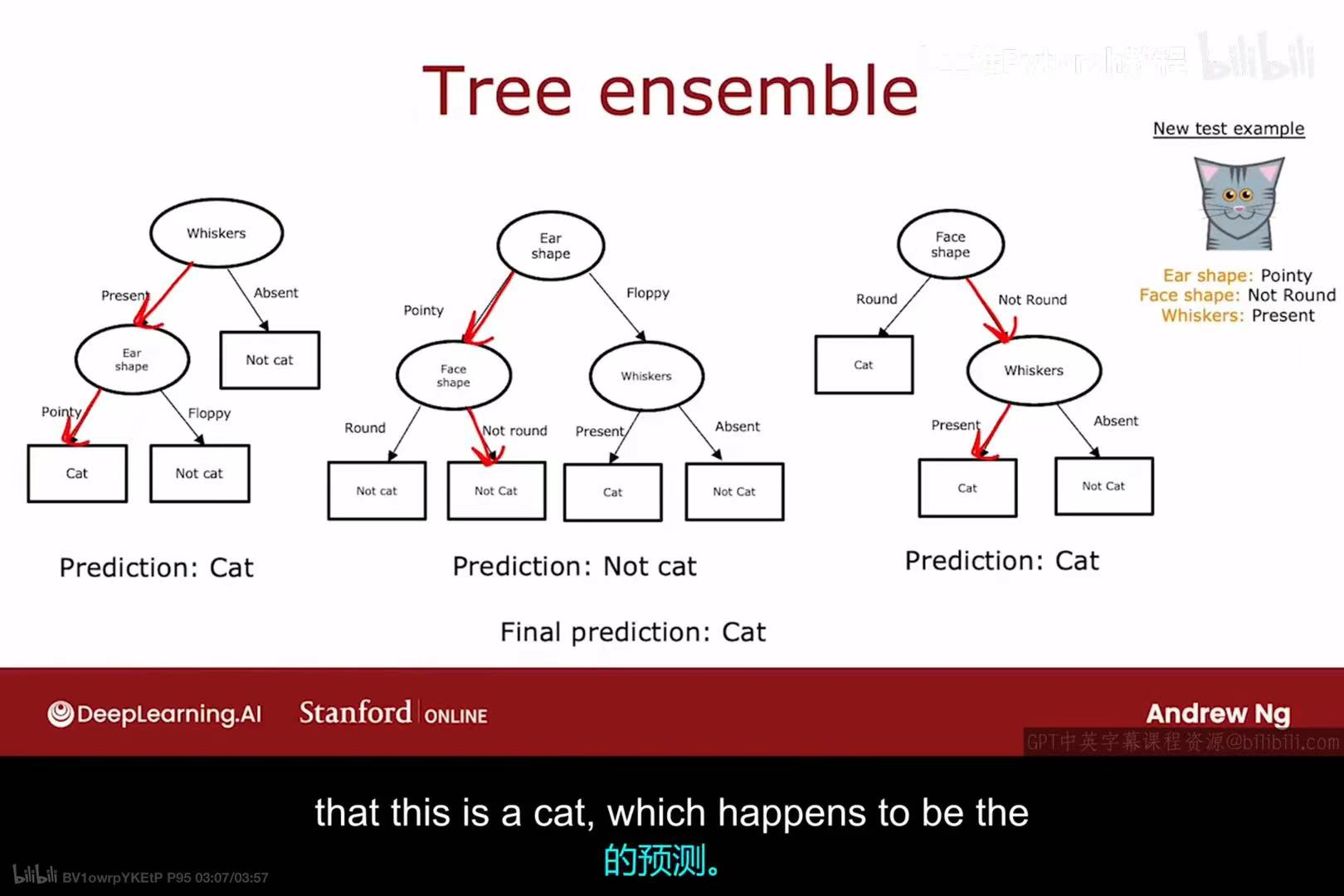
为了解决单个决策树不稳定的问题，我们可以使用树集成（Tree ensemble的方法。

核心思想：不只训练一棵树，而是训练多棵不同的决策树。
预测方法 ：当对新样本进行预测时，让这多棵树分别进行预测，然后通过"投票"的方式（少数服从多数）来决定最终的预测结果。
效果：集成多个不同模型的预测，通常可以得到比任何单个模型更准确、更稳定的结果。

3.3 Bagging 与随机森林

Bagging（Bootstrap Aggregating） 是构建树集成的一种常用技术。

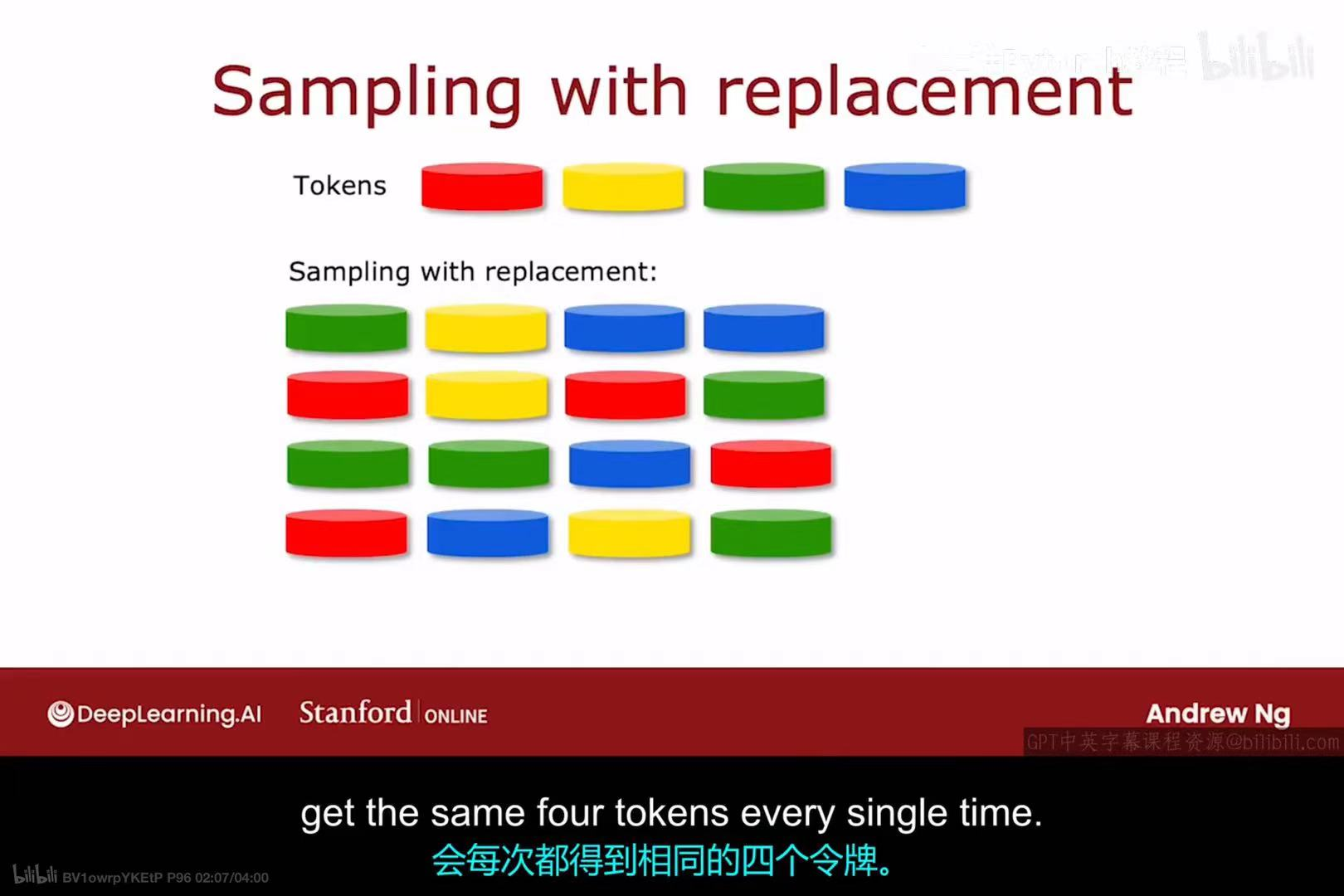
它的基础是有放回抽样（Sampling with replacement） ，也称为自助法（Bootstrap） 。这意味着从一个大小为 m 的数据集中抽取一个样本时，我们会把它放回，所以它有可能被再次抽中。通过这种方式，我们可以从原始数据集中生成多个大小相同但内容不同的新数据集。

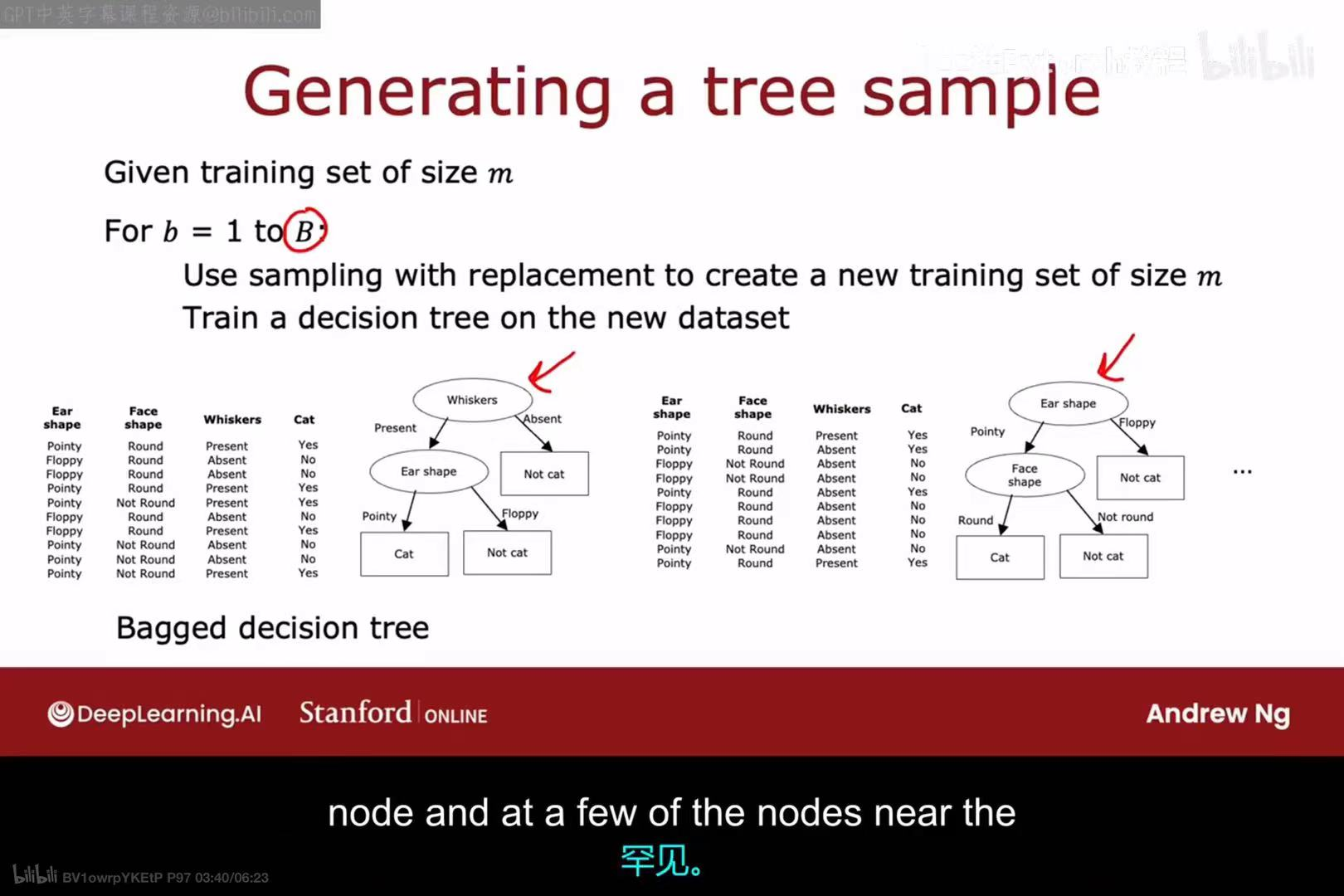
Bagging 算法流程：

给定一个大小为 m 的训练集。
循环 B 次（例如 B=100）：
a. 使用有放回抽样，从原始训练集中创建一个新的、大小为 m 的训练集。
b. 在这个新的数据集上训练一棵决策树。
最终得到一个由 B 棵决策树组成的集成，称为袋装决策树（Bagged decision tree）。

随机森林（Random Forest） 算法在Bagging的基础上增加了一步，以进一步增强树之间的差异性：

在Bagging的每一步训练决策树时，当需要在某个节点选择分裂特征时，算法并不会考虑所有 n 个可用的特征。
相反，它会先从 n 个特征中，随机选择一个大小为 k 的子集 （其中 k < n，一个常见的经验法则是 k = sqrt(n)）。
然后，算法只在这个 k 个特征的子集中，寻找信息增益最大或方差缩减最大的最佳分裂特征。

这种对特征的随机化选择，确保了集成中的每棵树都有很大的不同，从而进一步降低了模型的方差，使得随机森林成为一个非常强大和鲁棒的算法。

3.4 提升法与XGBoost

**提升法（Boosting）**是构建树集成的另一种核心技术。

与Bagging中并行、独立地训练多棵树不同，提升法是串行的：

它首先训练一棵树。
然后，它会分析这棵树的错误，并提高那些被错误分类的样本的权重。
接着，它训练第二棵树，这棵树会更加关注那些在第一步中被分错的"困难"样本。
这个过程会持续进行 B 轮，每一棵新的树都致力于修正前面所有树留下的残差或错误。
最终，所有树的预测会以某种加权方式结合起来，形成最终预测。

XGBoost (eXtreme Gradient Boosting) 是提升树算法的一个高度优化和流行的实现。它之所以被广泛使用，是因为：

它是一个开源、快速且高效的实现。
它内置了优秀的分裂标准和停止分裂的准则。
它包含了正则化项来防止过拟合。
它在机器学习竞赛（如Kaggle）中表现极其出色，是一个非常有竞争力的算法。

在实践中使用XGBoost非常直接。像scikit-learn一样，它提供了简单的API：

分类任务 ：使用 XGBClassifier。
回归任务 ：使用 XGBRegressor。
使用时，只需导入相应的类，创建模型实例，然后调用 .fit() 方法进行训练，再调用 .predict() 方法进行预测。

四决策树与神经网络的对比

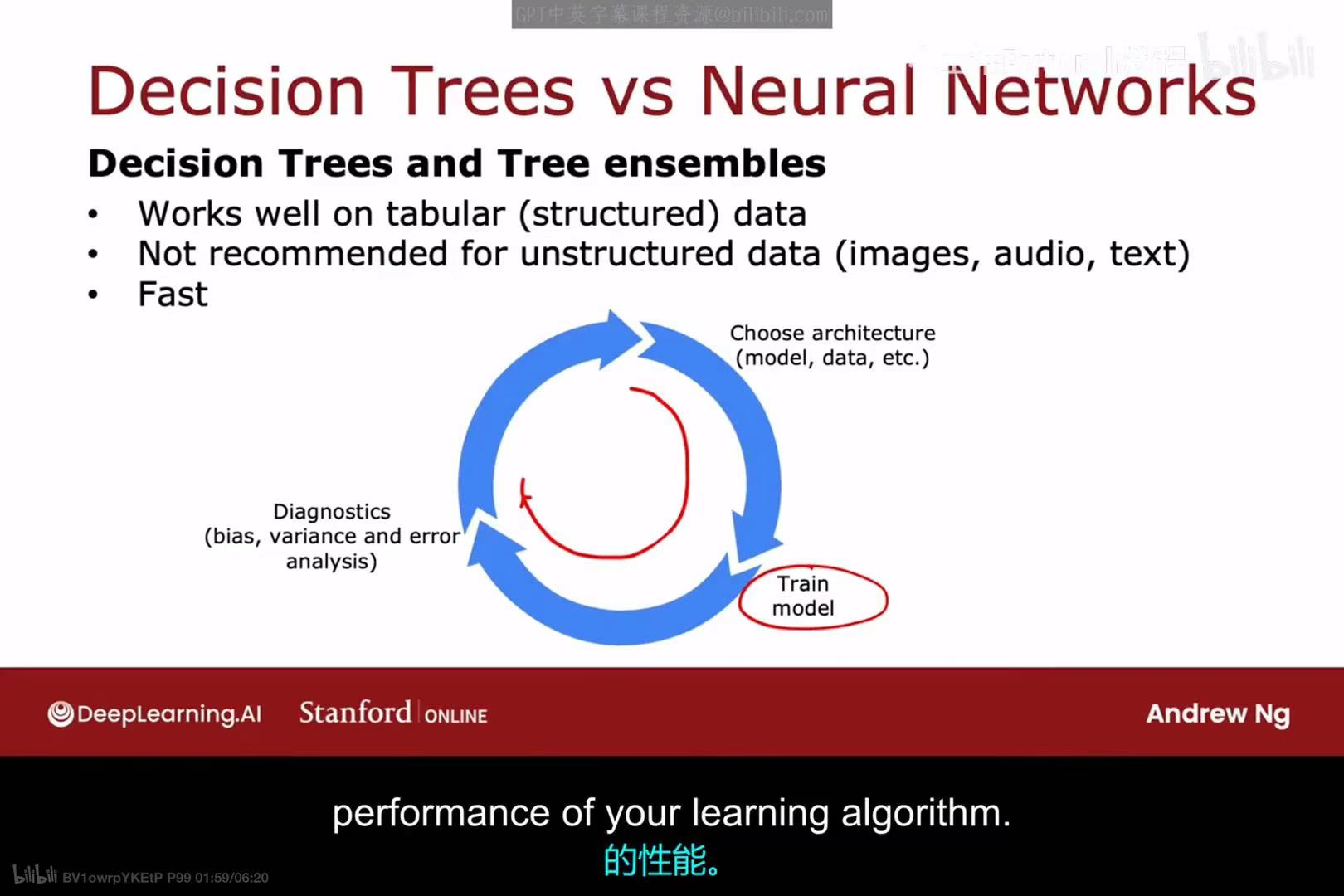
决策树（及其集成）和神经网络都是强大的模型，但它们各有优劣，适用于不同的场景。

决策树和树集成（如随机森林, XGBoost）：

优点：
- 在表格数据（或称结构化数据上表现非常好。这是它们最擅长的领域。
- 训练和预测速度通常很快。
- 单个的小决策树具有很好的可解释性，人类可以直观地理解其决策逻辑。
缺点：
- 不推荐用于非结构化数据，如图像、音频和文本。

神经网络：

优点：
- 在所有类型的数据上都表现出色，包括结构化和非结构化数据。
- 在处理图像、音频、文本等非结构化数据时，是目前最先进的方法。
- 可以很好地与迁移学习结合使用。
- 在构建由多个模型协同工作的复杂系统时，将多个神经网络串联起来可能更容易。
缺点：
- 训练和推理可能比决策树慢。
- 通常被认为是"黑箱"模型，可解释性较差。