目录
前言:
在计算机科学的发展历程中,算法作为解决计算问题的核心手段,始终扮演着不可或缺的角色。面对海量数据与复杂业务场景带来的挑战,如何高效地组织、处理与排序信息,成为程序设计中的基础性课题。在众多经典算法中,排序算法以其普适性与代表性,成为衡量算法效率与思想深度的重要标尺。
从最直观的冒泡排序到高度优化的快速排序,从稳定有序的归并排序到基于堆结构的堆排序,十大排序算法不仅涵盖了不同的时间与空间复杂度特征,更体现了分治、递归、交换、选择等核心编程思想的巧妙运用。它们不仅是学习算法入门的必经之路,更是深入理解数据处理逻辑、性能分析与实际工程应用的重要基石。
本文将系统梳理十大经典排序算法的原理、实现方式与适用场景,结合代码示例与复杂度分析,帮助读者构建完整的排序知识体系,为后续算法进阶与实际开发提供坚实的理论支撑。
一、冒泡排序
时间复杂度分析:最差为逆序O(N^2),最好是有序为O(N),在其中加一个判断器.
空间复杂度分析:O(1),没有额外开辟空间
//冒泡排序
void BubbleSort(int* arr, int size)
{
for (int i = 0; i < size - 1; i++)
{
int flag = 0;
for (int j = 0; j < size - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
Swap(&arr[j], &arr[j + 1]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
}
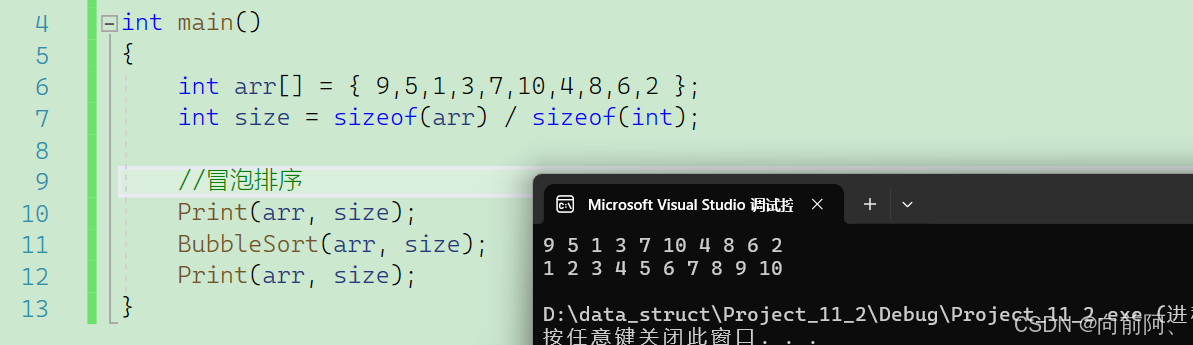
}测试结果如下:
二、堆排序
时间复杂度分析:O(N*logN)
空间复杂度:O(1)
//堆排序
void big_AdjustDown(int* arr, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && arr[child + 1] > arr[child])
{
child++;
}
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
void HeapSort(int* arr, int size)
{
//首先向下调整建堆
for (int i = (size - 1 - 1) / 2 ; i >= 0 ; i--)
{
big_AdjustDown(arr, size, i);
}
//此时开始交换
int end = size - 1;
while (end>0)
{
Swap(&arr[0], &arr[end]);
big_AdjustDown(arr, end, 0);
end--;
}
}测试结果如下:

三、插入排序
时间复杂度:最坏逆序为O(N^2),最好顺序为O(N)
空间复杂度:O(1)
//插入排序
void InsertSort(int* arr, int size)
{
for (int i = 0; i < size - 1; i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}测试结果如下

四、希尔排序
时间复杂度(很难算,直接背):O(N^1.3)
空间复杂度:O(1)
//希尔排序
void ShellSort(int* arr, int size)
{
int gap = size;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < size - gap; i++)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end = end - gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}测试结果如下:

五、选择排序
时间复杂度:O(N^2)
空间复杂度:O(1)
//选择排序--从双边一起走
void SelectSort(int* arr, int size)
{
int begin = 0;
int end = size - 1;
int maxi = begin;
int mini = begin;
while (begin < end)
{
for (int i = begin + 1; i <= end; i++)
{
if (arr[maxi] < arr[i])
{
maxi = i;
}
if (arr[mini] > arr[i])
{
mini = i;
}
}
//一轮找一个最大值和一个最小值
Swap(&arr[begin], &arr[mini]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&arr[maxi], &arr[end]);
begin++;
end--;
}
}测试结果如下:

六、快速排序--hoar版本
时间复杂度:O(N*logN)
空间复杂度:O(1)
//快速排序--hoar版本
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int keyi = left;
while (begin < end)
{
//右边找小
while (begin < end && arr[end] >= arr[keyi])
{
end--;
}
//左边找大
while (begin < end && arr[begin] <= arr[keyi])
{
begin++;
}
//此时说明找到了
Swap(&arr[end], &arr[begin]);
}
//此时说明begin==end
Swap(&arr[keyi], &arr[begin]);
keyi = begin;
//此时区间被分割成[left,keyi-1],keyi,[keyi+1,right]
QuickSort(arr, left, keyi - 1);
QuickSort(arr, keyi + 1, right);
}测试结果如下:

七、快速排序--挖坑法
//快速排序的挖坑法
void QuickSort_hole(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int hole = left;
int key = arr[left];
while (begin < end)
{
//右边找大
while (begin < end && arr[end] >= key)
{
end--;
}
//此时说明右边已经找到大的了
if (begin < end)
{
arr[hole] = arr[end];
hole = end;
}
//左边找大
while (begin < end && arr[begin] <= key)
{
begin++;
}
//此时说明已经找到了
if (begin < end)
{
arr[hole] = arr[begin];
hole = begin;
}
}
//此时说明相等
arr[hole] = key;
//此时区间被分成[left,hole-1][hole+1,right]
QuickSort_hole(arr, left, hole - 1);
QuickSort_hole(arr, hole + 1, right);
}测试结果如下:

八、快速排序--双指针法
//快速排序双指针法
void Quick_sort_p(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
if (arr[cur] < arr[keyi])
{
prev++;
Swap(&arr[prev], &arr[cur]);
}
cur++;
}
//此时prev是中间值坐标
Swap(&arr[keyi], &arr[prev]);
keyi = prev;
Quick_sort_p(arr, left, keyi - 1);
Quick_sort_p(arr, keyi + 1, right);
}测试结果如下:

九、快速排序--非递归实现
(需要借助栈,前几篇文章有,这边就不详细贴代码了)
//快速排序的非递归实现--需要借助栈
int Quick_sort_single(int* arr, int left, int right)
{
int keyi = left;
int begin = left;
int end = right;
while (begin < end)
{
//右边找小
while (begin < end && arr[end] >= arr[keyi])
{
end--;
}
//左边找大
while (begin < end && arr[begin] <= arr[keyi])
{
begin++;
}
//此时找到了
Swap(&arr[end], &arr[begin]);
}
Swap(&arr[keyi], &arr[begin]);
keyi = begin;
return keyi;
}
void QuickSortNonR(int* arr, int left, int right)
{
//创建栈并初始化
ST st;
STInit(&st);
//先将右边压入栈,再将左边压入栈
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
int keyi = Quick_sort_single(arr, begin, end);
//此时区间已经被分成[begin,keyi-1][keyi+1,end];
//继续压栈
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (begin < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
//栈的销毁
STDestory(&st);
}测试结果如下

十、归并排序--递归实现
//归并排序的递归实现
void _MergeSort(int* arr, int* tmp, int left, int right)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
_MergeSort(arr, tmp, left, mid);
_MergeSort(arr, tmp, mid + 1, right);
//此时开始排序
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if(arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
memcpy(arr + left, tmp + left, (right - left + 1)*sizeof(int));
}
void MergeSort(int* arr, int size)
{
//首先创建一个数组,用于套换
int* tmp = (int*)malloc(sizeof(int) * size);
if (tmp == NULL)
{
perror("malloc fail!");
return NULL;
}
_MergeSort(arr, tmp, 0, size - 1);
free(tmp);
tmp = NULL;
}十一、归并排序--非递归实现
//归并排序的非递归实现
void MergeSort_NonR(int* arr, int size)
{
int* tmp = (int*)malloc(sizeof(int)*size);
if (tmp == NULL)
{
perror("malloc fail!");
return;
}
int gap = 1;
while (gap < size)
{
for (int i = 0; i < size; i = i + 2 * gap)
{
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
if (begin2 >= size)
{
break;
}
if (end2 >= size)
{
end2 = size - 1;
}
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[j++] = arr[begin1++];
}
else
{
tmp[j++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2++];
}
memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap = 2 * gap;
}
}测试结果如下:

十二、非比较排序--计数排序
//非比较排序
void Count_Sort(int* arr, int size)
{
int min = arr[0];
int max = arr[0];
//寻找最大值和最小值
for (int i = 0; i < size; i++)
{
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
//防止空间浪费,所以找最大值和最小值,求值所在的区间
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
if (count == NULL)
{
perror("calloc fail!");
return;
}
//统计次数
for (int i = 0; i < size; i++)
{
count[arr[i] - min]++;
}
//往原数组里面插入数据,记得加上min
int cur = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
arr[cur++] = i + min;
}
}
}测试结果如下
