算法基础篇：（二十一）数据结构之单调栈：从原理到实战，玩转高效解题

目录

前言

[一、什么是单调栈？先打破 "栈" 的常规认知](#一、什么是单调栈？先打破 “栈” 的常规认知)

[1.1 单调栈的核心特性](#1.1 单调栈的核心特性)

[1.2 如何实现一个单调栈？](#1.2 如何实现一个单调栈？)

实现单调递增栈

实现单调递减栈

[1.3 核心操作解析：为什么要 "弹出元素"？](#1.3 核心操作解析：为什么要 “弹出元素”？)

二、单调栈能解决什么问题？四大核心场景全覆盖

[2.1 场景 1：找左侧最近的 "更大元素"](#2.1 场景 1：找左侧最近的 “更大元素”)

问题描述

解题思路

代码实现

测试用例验证

[2.2 场景 2：找左侧最近的 "更小元素"](#2.2 场景 2：找左侧最近的 “更小元素”)

问题描述

解题思路

代码实现

测试用例验证

[2.3 场景 3：找右侧最近的 "更大元素"](#2.3 场景 3：找右侧最近的 “更大元素”)

问题描述

解题思路

代码实现

测试用例验证

[2.4 场景 4：找右侧最近的 "更小元素"](#2.4 场景 4：找右侧最近的 “更小元素”)

问题描述

解题思路

代码实现

测试用例验证

[三、模板题实战：洛谷 P5788 【模板】单调栈](#三、模板题实战：洛谷 P5788 【模板】单调栈)

[3.1 题目描述](#3.1 题目描述)

[3.2 输入输出要求](#3.2 输入输出要求)

[3.3 解题思路](#3.3 解题思路)

[3.4 完整代码实现](#3.4 完整代码实现)

[3.5 测试用例验证](#3.5 测试用例验证)

四、进阶实战：单调栈的经典应用场景

[4.1 实战 1：发射站（洛谷 P1901）](#4.1 实战 1：发射站（洛谷 P1901）)

题目描述

解题思路

完整代码

测试用例验证

[4.2 实战 2：柱状图中最大的矩形（洛谷 HISTOGRA）](#4.2 实战 2：柱状图中最大的矩形（洛谷 HISTOGRA）)

题目描述

解题思路

完整代码

测试用例验证

五、单调栈的核心总结与避坑指南

[5.1 核心总结](#5.1 核心总结)

[5.2 避坑指南](#5.2 避坑指南)

总结

---

前言

在算法的世界里，数据结构是解决问题的基石，而单调栈绝对是其中 "低调又强大" 的存在。它看似只是普通栈的 "升级版"，却能将原本需要 O (n²) 时间复杂度的问题，一键优化到 O (n)，堪称处理 "找最近最值" 类问题的 "神器"。本文将从单调栈的核心原理讲起，结合实战例题，手把手带你吃透单调栈的用法，让你彻底搞懂这一高频面试 / 竞赛考点。下面就让我们正式开始吧！

---

一、什么是单调栈？先打破 "栈" 的常规认知

提到栈，大家首先想到的是 "先进后出" 的线性结构，而单调栈 ，顾名思义，就是在普通栈的基础上，给元素加上了 "单调性" 的约束 ------ 栈内的元素必须严格保持递增或递减（也可根据需求调整为非严格递增 / 递减）。

1.1 单调栈的核心特性

• 本质还是栈：完全遵循栈的 "先进后出" 规则，只是多了 "维护单调性" 的操作；
• 单调性可控：可维护单调递增栈（栈底到栈顶元素从小到大），也可维护单调递减栈（栈底到栈顶元素从大到小）；
• 操作高效：每个元素最多入栈一次、出栈一次，整体时间复杂度稳定在 O (n)。

1.2 如何实现一个单调栈？

话不多说，先看基础代码实现。我们以 C++ 为例，分别实现单调递增栈和单调递减栈：

实现单调递增栈

#include <iostream>
#include <stack>
using namespace std;

const int N = 3e6 + 10; // 适配大数据量场景
int a[N], n;

// 维护单调递增栈：栈内元素从小到大
void monotonicIncreasingStack() {
    stack<int> st;
    for (int i = 1; i <= n; i++) {
        // 关键操作：弹出所有大于等于当前元素的栈顶元素，保证单调性
        while (st.size() && st.top() >= a[i]) {
            st.pop();
        }
        st.push(a[i]); // 插入当前元素，栈仍保持递增
    }
}

实现单调递减栈

// 维护单调递减栈：栈内元素从大到小
void monotonicDecreasingStack() {
    stack<int> st;
    for (int i = 1; i <= n; i++) {
        // 关键操作：弹出所有小于等于当前元素的栈顶元素，保证单调性
        while (st.size() && st.top() <= a[i]) {
            st.pop();
        }
        st.push(a[i]); // 插入当前元素，栈仍保持递减
    }
}

1.3 核心操作解析：为什么要 "弹出元素"？

大家可能会疑惑："为什么要先弹出元素再入栈？" 其实这正是单调栈的核心 ------为了保证栈的单调性不被破坏。

比如维护单调递增栈时，若当前元素a[i]比栈顶元素小，说明栈顶元素 "挡路" 了：如果直接入栈，栈就会出现 "大元素在前、小元素在后" 的情况，违背递增规则。因此需要先弹出所有≥a[i]的元素，直到栈顶元素＜a[i]（或栈为空），再将**a[i]**入栈。

举个直观的例子：假设数组a = [5, 3, 7, 2]，维护单调递增栈的过程：

1. i=1，a [i]=5：栈空，直接入栈 → 栈：[5]
2. i=2，a [i]=3：栈顶 5≥3，弹出 5；栈空，入栈 3 → 栈：[3]
3. i=3，a [i]=7：栈顶 3＜7，直接入栈 → 栈：[3,7]
4. i=4，a [i]=2：栈顶 7≥2，弹出 7；栈顶 3≥2，弹出 3；栈空，入栈 2 → 栈：[2]

最终栈内元素为 [2]，完美保持递增特性。

二、单调栈能解决什么问题？四大核心场景全覆盖

单调栈的核心应用场景，总结起来就是 "找最近最值"------ 给定一个元素，找到它左侧 / 右侧最近的、比它大 / 小的元素的位置。这四类问题看似不同，实则原理相通，掌握一种就能举一反三。

先记住一句 "口诀"：找左侧，正遍历；找右侧，逆遍历；比它大，单调减；比它小，单调增。这句话能帮你快速确定遍历方向和栈的单调性，下文会反复验证。

2.1 场景 1：找左侧最近的 "更大元素"

问题描述

给定数组a，对于每个元素a[i]，找到其左侧第一个比它大的元素的下标；若不存在，返回 0。

解题思路

• 遍历方向：从左到右（找左侧元素，正序遍历）；
• 栈的单调性：维护单调递减栈（要找 "更大" 的元素，栈内元素从大到小，保证栈顶是最近的更大值）；
• 栈内存储：元素下标（最终要返回位置，存下标比存值更实用）。

代码实现

#include <iostream>
#include <stack>
using namespace std;

const int N = 3e6 + 10;
int a[N], n;
int ret[N]; // 存储每个元素的答案

void findLeftLarger() {
    stack<int> st; // 单调递减栈，存下标
    for (int i = 1; i <= n; i++) {
        // 弹出所有≤a[i]的元素，剩下的栈顶就是左侧最近的更大元素
        while (st.size() && a[st.top()] <= a[i]) {
            st.pop();
        }
        // 栈非空则栈顶是答案，否则为0
        if (st.size()) {
            ret[i] = st.top();
        } else {
            ret[i] = 0;
        }
        st.push(i); // 入栈当前下标，维护栈的单调性
    }
    // 输出结果
    for (int i = 1; i <= n; i++) {
        cout << ret[i] << " ";
    }
    cout << endl;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    findLeftLarger();
    return 0;
}

测试用例验证

输入：

9
1 4 10 6 3 3 15 21 8

输出：

0 0 0 3 4 4 0 0 8

解释：

• 第 3 个元素 10，左侧最近的更大元素不存在 → 0；
• 第 4 个元素 6，左侧最近的更大元素是 10（下标 3） → 3；
• 第 9 个元素 8，左侧最近的更大元素是 21（下标 8） → 8。

2.2 场景 2：找左侧最近的 "更小元素"

问题描述

给定数组a，对于每个元素a[i]，找到其左侧第一个比它小的元素的下标；若不存在，返回 0。

解题思路

• 遍历方向：从左到右；
• 栈的单调性：维护单调递增栈（要找 "更小" 的元素，栈内元素从小到大，栈顶是最近的更小值）；
• 栈内存储：元素下标。

代码实现

#include <iostream>
#include <stack>
using namespace std;

const int N = 3e6 + 10;
int a[N], n;
int ret[N];

void findLeftSmaller() {
    stack<int> st; // 单调递增栈，存下标
    for (int i = 1; i <= n; i++) {
        // 弹出所有≥a[i]的元素，剩下的栈顶就是左侧最近的更小元素
        while (st.size() && a[st.top()] >= a[i]) {
            st.pop();
        }
        ret[i] = st.size() ? st.top() : 0;
        st.push(i);
    }
    // 输出结果
    for (int i = 1; i <= n; i++) {
        cout << ret[i] << " ";
    }
    cout << endl;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    findLeftSmaller();
    return 0;
}

测试用例验证

输入：

9
1 4 10 6 3 3 15 21 8

输出：

0 1 2 2 1 1 6 7 6

解释：

• 第 4 个元素 6，左侧最近的更小元素是 4（下标 2） → 2；
• 第 5 个元素 3，左侧最近的更小元素是 1（下标 1） → 1；
• 第 9 个元素 8，左侧最近的更小元素是 15（下标 6） → 6。

2.3 场景 3：找右侧最近的 "更大元素"

问题描述

给定数组a，对于每个元素a[i]，找到其右侧第一个比它大的元素的下标；若不存在，返回 0。

解题思路

• 遍历方向：从右到左（找右侧元素，逆序遍历）；
• 栈的单调性：维护单调递减栈（找 "更大" 的元素，栈内递减）；
• 栈内存储：元素下标。

代码实现

#include <iostream>
#include <stack>
using namespace std;

const int N = 3e6 + 10;
int a[N], n;
int ret[N];

void findRightLarger() {
    stack<int> st; // 单调递减栈，存下标
    for (int i = n; i >= 1; i--) {
        // 弹出所有≤a[i]的元素，剩下的栈顶就是右侧最近的更大元素
        while (st.size() && a[st.top()] <= a[i]) {
            st.pop();
        }
        ret[i] = st.size() ? st.top() : 0;
        st.push(i);
    }
    // 输出结果
    for (int i = 1; i <= n; i++) {
        cout << ret[i] << " ";
    }
    cout << endl;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    findRightLarger();
    return 0;
}

测试用例验证

输入：

9
1 4 10 6 3 3 15 21 8

输出：

2 3 7 7 7 7 8 0 0

解释：

• 第 1 个元素 1，右侧最近的更大元素是 4（下标 2） → 2；
• 第 7 个元素 15，右侧最近的更大元素是 21（下标 8） → 8；
• 第 8 个元素 21，右侧无更大元素 → 0。

2.4 场景 4：找右侧最近的 "更小元素"

问题描述

给定数组a，对于每个元素a[i]，找到其右侧第一个比它小的元素的下标；若不存在，返回 0。

解题思路

• 遍历方向：从右到左；
• 栈的单调性：维护单调递增栈（找 "更小" 的元素，栈内递增）；
• 栈内存储：元素下标。

代码实现

#include <iostream>
#include <stack>
using namespace std;

const int N = 3e6 + 10;
int a[N], n;
int ret[N];

void findRightSmaller() {
    stack<int> st; // 单调递增栈，存下标
    for (int i = n; i >= 1; i--) {
        // 弹出所有≥a[i]的元素，剩下的栈顶就是右侧最近的更小元素
        while (st.size() && a[st.top()] >= a[i]) {
            st.pop();
        }
        ret[i] = st.size() ? st.top() : 0;
        st.push(i);
    }
    // 输出结果
    for (int i = 1; i <= n; i++) {
        cout << ret[i] << " ";
    }
    cout << endl;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    findRightSmaller();
    return 0;
}

测试用例验证

输入：

9
1 4 10 6 3 3 15 21 8

输出：

0 5 4 5 0 0 9 9 0

解释：

• 第 2 个元素 4，右侧最近的更小元素是 3（下标 5） → 5；
• 第 3 个元素 10，右侧最近的更小元素是 6（下标 4） → 4；
• 第 7 个元素 15，右侧最近的更小元素是 8（下标 9） → 9。

三、模板题实战：洛谷 P5788 【模板】单调栈

光说不练假把式，我们以洛谷经典模板题为例，完整拆解单调栈的解题流程。

题目链接：https://www.luogu.com.cn/problem/P5788

3.1 题目描述

给出项数为n的整数数列a[1...n]，定义函数f(i)代表数列中第i个元素之后第一个大于a[i]的元素的下标，即f(i)=min{ j | i<j ≤n, a[j]>a[i] }。若不存在，f(i)=0。试求出f(1...n)。

3.2 输入输出要求

• 输入：第一行正整数n，第二行n个正整数a[1...n]；
• 输出：一行n个整数，表示f(1),f(2),...,f(n)；
• 数据范围：1≤n≤3×10⁶，1≤a [i]≤10⁹。

3.3 解题思路

这道题本质是**"找右侧最近的更大元素"**，直接套用前文的思路：

• 遍历方向：从右到左；
• 栈的单调性：单调递减栈；
• 栈内存储：元素下标。

3.4 完整代码实现

#include <iostream>
#include <stack>
using namespace std;

const int N = 3e6 + 10; // 适配3e6的大数据量
int n;
int a[N];
int ret[N]; // 存储每个元素的答案

int main() {
    ios::sync_with_stdio(false); // 关闭同步，加速输入输出
    cin.tie(0); // 解绑cin和cout

    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    stack<int> st; // 单调递减栈，存下标
    for (int i = n; i >= 1; i--) {
        // 弹出所有≤a[i]的元素，保证栈的单调性
        while (st.size() && a[st.top()] <= a[i]) {
            st.pop();
        }
        // 栈顶即为右侧最近的更大元素下标
        ret[i] = st.size() ? st.top() : 0;
        st.push(i); // 入栈当前下标
    }

    // 输出结果
    for (int i = 1; i <= n; i++) {
        cout << ret[i] << " ";
    }
    cout << endl;

    return 0;
}

3.5 测试用例验证

输入：

5
1 4 2 3 5

输出：

2 5 4 5 0

解释：

• a[1]=1，右侧最近的更大元素是a[2]=4 → f(1)=2；
• a[2]=4，右侧最近的更大元素是a[5]=5 → f(2)=5；
• a[3]=2，右侧最近的更大元素是a[4]=3 → f(3)=4；
• a[4]=3，右侧最近的更大元素是a[5]=5 → f(4)=5；
• a[5]=5，右侧无更大元素 → f (5)=0。

四、进阶实战：单调栈的经典应用场景

除了基础的 "找最近最值"，单调栈还能解决很多经典算法题，下面选取两个高频考点，带你深入理解。

4.1 实战 1：发射站（洛谷 P1901）

题目链接：https://www.luogu.com.cn/problem/P1901

题目描述

某地有N个能量发射站排成一行，每个发射站i有高度H[i]和能量值V[i]，发射的能量只被两边最近的且比它高的发射站接收。求接收最多能量的发射站的能量值。

解题思路

• 核心需求：对每个发射站，找到左侧 / 右侧最近的更高发射站，将能量值累加到对应发射站；
• 左侧更高：正序遍历，维护单调递减栈（找更高元素）；
• 右侧更高：逆序遍历，维护单调递减栈；
• 最终遍历所有发射站的能量总和，取最大值。

完整代码

#include <iostream>
#include <stack>
using namespace std;

typedef long long LL; // 防止能量值溢出
const int N = 1e6 + 10;

int n;
LL h[N], v[N];
LL sum[N]; // 存储每个发射站接收的总能量

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> h[i] >> v[i];
    }

    // 第一步：找左侧最近的更高发射站
    stack<int> st;
    for (int i = 1; i <= n; i++) {
        // 弹出所有≤当前高度的元素，栈顶即为左侧最近更高
        while (st.size() && h[st.top()] <= h[i]) {
            st.pop();
        }
        if (st.size()) {
            sum[st.top()] += v[i]; // 能量累加到左侧更高的发射站
        }
        st.push(i);
    }

    // 第二步：找右侧最近的更高发射站（清空栈，重新遍历）
    while (st.size()) st.pop();
    for (int i = n; i >= 1; i--) {
        while (st.size() && h[st.top()] <= h[i]) {
            st.pop();
        }
        if (st.size()) {
            sum[st.top()] += v[i]; // 能量累加到右侧更高的发射站
        }
        st.push(i);
    }

    // 第三步：找接收能量的最大值
    LL ret = 0;
    for (int i = 1; i <= n; i++) {
        ret = max(ret, sum[i]);
    }
    cout << ret << endl;

    return 0;
}

测试用例验证

输入：

3
4 2
3 5
6 10

输出：7

解释：

• 发射站 1（H=4，V=2）：右侧最近更高是发射站 3，能量 2 传给 3；
• 发射站 2（H=3，V=5）：右侧最近更高是发射站 3，能量 5 传给 3；
• 发射站 3（H=6，V=10）：无更高发射站，无能量接收；
• 总接收：发射站 3 接收 2+5=7，为最大值。

4.2 实战 2：柱状图中最大的矩形（洛谷 HISTOGRA）

题目链接：https://www.luogu.com.cn/problem/SP1805

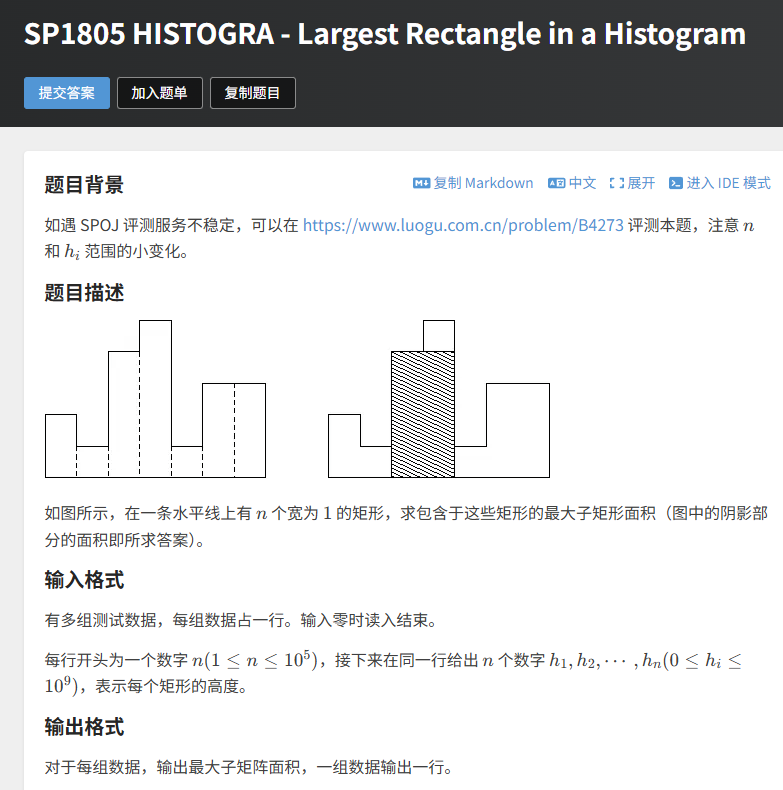
题目描述

给定n个宽度为 1 的矩形的高度，求包含于这些矩形的最大子矩形面积。

解题思路

• 核心思路：对每个矩形i，找到左侧 / 右侧最近的更矮矩形，确定该矩形能扩展的最大宽度，面积 = 高度 × 宽度；
• 左侧更矮：正序遍历，维护单调递增栈；
• 右侧更矮：逆序遍历，维护单调递增栈；
• 遍历所有矩形的面积，取最大值。

完整代码

#include <iostream>
#include <stack>
using namespace std;

typedef long long LL; // 防止面积溢出
const int N = 1e5 + 10;

int n;
LL h[N];
LL left_bound[N], right_bound[N]; // 左侧/右侧最近更矮矩形的下标

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n, n) { // 输入0结束
        for (int i = 1; i <= n; i++) {
            cin >> h[i];
        }

        // 第一步：找左侧最近的更矮矩形
        stack<int> st;
        for (int i = 1; i <= n; i++) {
            while (st.size() && h[st.top()] >= h[i]) {
                st.pop();
            }
            left_bound[i] = st.size() ? st.top() : 0;
            st.push(i);
        }

        // 第二步：找右侧最近的更矮矩形
        while (st.size()) st.pop();
        for (int i = n; i >= 1; i--) {
            while (st.size() && h[st.top()] >= h[i]) {
                st.pop();
            }
            right_bound[i] = st.size() ? st.top() : n + 1;
            st.push(i);
        }

        // 第三步：计算最大面积
        LL ret = 0;
        for (int i = 1; i <= n; i++) {
            LL width = right_bound[i] - left_bound[i] - 1;
            ret = max(ret, h[i] * width);
        }
        cout << ret << endl;
    }

    return 0;
}

测试用例验证

输入：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出：

8
4000

解释：

• 第一组数据：最大矩形是高度为 3、宽度为 2（下标 6-7），或高度为 4、宽度为 2（下标 3-4），面积 8；
• 第二组数据：4 个高度 1000 的矩形，宽度 4，面积 1000×4=4000。

五、单调栈的核心总结与避坑指南

5.1 核心总结

1. 单调性选择：
   • 找 "更大" 元素 → 维护单调递减栈；
   • 找 "更小" 元素 → 维护单调递增栈；
2. 遍历方向：
   • 找左侧元素 → 正序遍历；
   • 找右侧元素 → 逆序遍历；
3. 栈内存储：优先存下标（需返回位置时直接用，存值无法对应位置）；
4. 时间复杂度：每个元素入栈 / 出栈各一次，O (n)，适配大数据量（如 3e6）。

5.2 避坑指南

1. 数据范围：注意int和long long的选择，避免溢出（如面积、能量值计算）；
2. 输入输出优化：大数据量下需加ios::sync_with_stdio(false); cin.tie(0);，否则会超时；
3. 栈的清空：多次使用栈时，需先清空（while(st.size()) st.pop();）；
4. 边界处理：无对应元素时返回 0（或 n+1），需提前定义好边界值。

---

总结

单调栈看似简单，实则是 "贪心思想" 与 "栈结构" 的完美结合。它的核心价值在于将嵌套循环的暴力解法，优化为线性时间复杂度，这也是算法优化的核心思路 ------ 用空间换时间，用数据结构约束逻辑。

掌握单调栈，不仅能解决 "找最近最值" 类问题，更能理解 "如何通过维护数据结构的特性来简化问题"。建议大家结合本文的例题，手动模拟栈的入栈、出栈过程，真正吃透每一步操作的意义。相信通过反复练习，你也能熟练运用单调栈，轻松应对算法面试和竞赛中的相关问题！

如果本文对你有帮助，欢迎点赞、收藏、关注～后续还会更新单调队列、并查集等数据结构的实战解析，敬请期待！