题目链接
题目描述
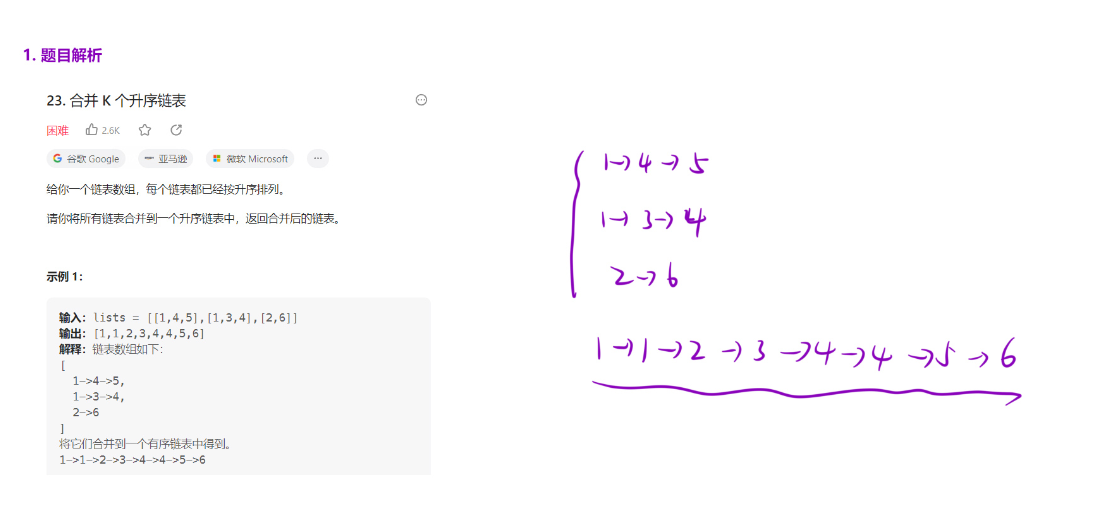
题目解析

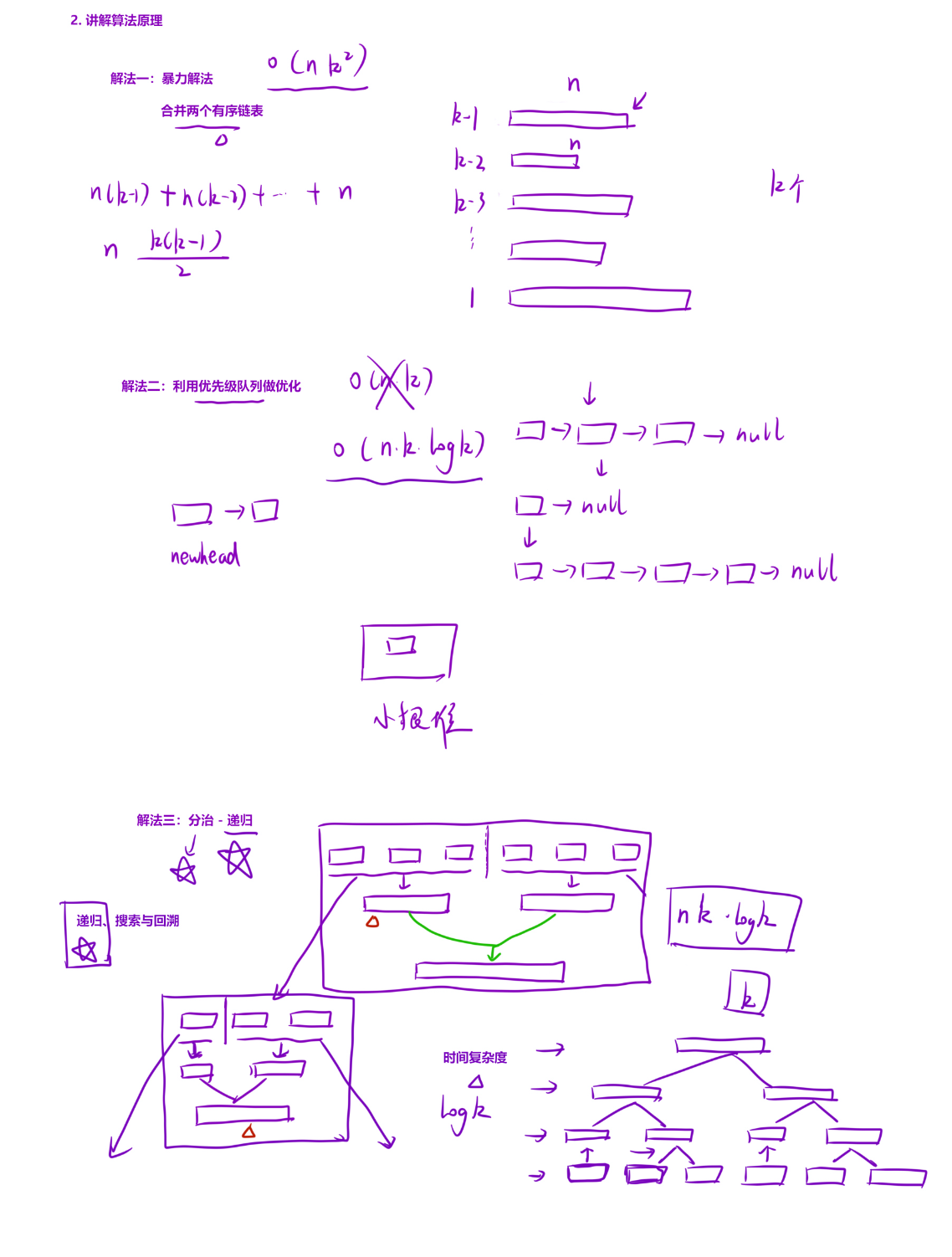
这段代码是 合并 K 个升序链表 的经典分治解法,核心思路是将 "多链表合并" 拆解为 "两两链表合并",利用递归分治降低时间复杂度。下面从「代码结构」「核心逻辑」「细节解析」「复杂度分析」四个维度完整解析:
一、代码整体结构
代码分为 3 个核心部分,职责清晰、层层递进:
|-------------------|------------------|------------------------------|
| 函数 | 作用 | 调用关系 |
| mergeKLists | 主函数(递归入口) | 调用 merge 启动分治 |
| merge | 分治函数(拆分 + 合并子问题) | 递归调用自身,最终调用mergeTwoLists |
| mergeTwoLists | 工具函数(合并两个升序链表) | 被 merge 调用,处理最小子问题 |
本质是 分治思想 的应用:把 K 个链表的大问题,拆成多个 "合并 2 个链表" 的小问题,最终合并小问题的结果。
二、核心逻辑拆解(以示例 1 为例)
示例 1 输入:lists = [[1,4,5],[1,3,4],[2,6]](3 个升序链表),核心流程如下:
1. 分治拆分(merge 函数的核心)
分治的本质是 "二分拆分",直到每个子问题只包含 0 或 1 个链表(递归终止条件):
- 初始区间:l=0, r=2(对应 3 个链表)
- 计算中点:mid = 0 + (2-0)/2 =
1,拆分为两个子区间:- 左子区间:[0,1](包含链表 1:1->4->5 和链表 2:1->3->4)
- 右子区间:[2,2](包含链表 3:2->6,触发终止条件 l==r,直接返回该链表)
- 继续拆分左子区间 [0,1]:
- 中点 mid=0,拆分为 [0,0](返回链表 1)和
[1,1](返回链表 2)
- 中点 mid=0,拆分为 [0,0](返回链表 1)和
拆分后得到 3 个 "单个链表":[1->4->5]、[1->3->4]、[2->6]。
2. 回溯合并(mergeTwoLists 函数的核心)
拆分到最小子问题后,开始 "回溯合并",每次合并两个升序链表:
- 第一步:合并 [1->4->5] 和 [1->3->4],得到 1->1->3->4->4->5(通过
mergeTwoLists实现) - 第二步:合并第一步结果与 [2->6],得到最终结果 1->1->2->3->4->4->5->6
整个过程类似 "归并排序":先拆分,再合并。
三、关键函数细节解析
1. 主函数 mergeKLists
cpp
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}- 作用:作为递归入口,直接调用分治函数merge ,传入整个链表数组的区间 [0, lists.size()-1]。
- 边界处理:若
lists为空(如示例 2),lists.size()-1 = -1,后续merge会处理l=0 > r=-1的情况,返回nullptr,符合预期。
2. 分治函数merge
cpp
ListNode* merge(vector<ListNode*>& lists, int l, int r) {
if (l > r) return nullptr; // 终止条件 1:无链表可合并
if (l == r) return lists[l]; // 终止条件 2:只有一个链表,直接返回
int mid = l + (r - l) / 2; // 二分中点(避免溢出,优于 (l+r)/2)
ListNode* left = merge(lists, l, mid); // 递归合并左区间
ListNode* right = merge(lists, mid+1, r); // 递归合并右区间
return mergeTwoLists(left, right); // 合并左右区间的结果
}- 递归终止条件:
- l > r:区间无效(比如
lists为空时,l=0, r=-1),返回nullptr(空链表)。 - l == r:区间内只有一个链表,无需合并,直接返回该链表(最小子问题的解)。
- l > r:区间无效(比如
- 二分中点计算:
mid = l + (r - l)/2是为了 避免整数溢出 (当l和r接近INT_MAX时,l+r会溢出,而这种写法不会)。 - 递归逻辑:先合并左半部分,再合并右半部分,最后将两部分的结果合并,体现 "分治 + 回溯"。
3. 两两合并函数mergeTwoLists
cpp
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode newHead; // 虚拟头节点(栈上分配,无需手动释放)
ListNode* curr = &newHead; // 游标指针,用于构建结果链表
// 双指针遍历两个链表,逐个比较节点值
while (l1 != nullptr && l2 != nullptr) {
if (l1->val <= l2->val) {
curr->next = l1; // 接入 l1 的当前节点
l1 = l1->next; // l1 指针后移
} else {
curr->next = l2; // 接入 l2 的当前节点
l2 = l2->next; // l2 指针后移
}
curr = curr->next; // 游标后移,准备接入下一个节点
}
// 接入剩余节点(其中一个链表已遍历完,剩余节点直接拼接)
curr->next = (l1 != nullptr) ? l1 : l2;
return newHead.next; // 虚拟头节点的下一个节点才是真正的头节点
}这是合并两个升序链表的 最优解法(双指针 + 虚拟头节点),细节关键:
- 虚拟头节点
newHead:- 作用:简化边界处理(无需判断结果链表是否为空,直接用
curr拼接节点)。 - 注意:
newHead是栈上对象,函数结束后自动销毁,不会内存泄漏(仅返回其next指针,指向堆上的链表节点)。
- 作用:简化边界处理(无需判断结果链表是否为空,直接用
- 双指针遍历:
l1和l2分别指向两个输入链表的当前节点,每次选 值较小的节点 接入结果链表,保证升序。
- 剩余节点拼接:
- 当一个链表遍历完(
l1或l2为nullptr),另一个链表的剩余节点直接拼接(因为输入链表本身是升序的,剩余节点无需再比较)。
- 当一个链表遍历完(
四、复杂度分析
1. 时间复杂度:O (N log k)
- 符号定义:
N是所有链表的总节点数,k是链表的个数。 - 分析:
- 分治的层数:将
k个链表拆分为 1 个链表,需要log k层(比如k=3时,层数为 2;k=4时,层数为 2)。 - 每层的合并时间:每一层需要合并所有
N个节点(因为每个节点只参与一次合并),时间为 O (N)。 - 总时间:
log k层 × 每层 O (N) = O (N log k),是该问题的最优时间复杂度。
- 分治的层数:将
2. 空间复杂度:O (log k)
- 递归栈空间:分治递归的深度为
log k(比如k=3时,递归深度为 2),栈空间为 O (log k)。 - 额外空间:除了递归栈,没有使用其他额外空间(虚拟头节点是栈上对象,不占额外堆空间),因此空间复杂度为 O (log k)。
五、边界情况处理
代码天然覆盖了题目中的所有边界案例:
- 案例 2(输入
lists = []):lists.size()=0,merge传入l=0, r=-1,触发l>r,返回nullptr,正确。 - 案例 3(输入
lists = [[]]):lists.size()=1,merge传入l=0, r=0,触发l==r,返回lists[0](空链表),正确。 - 部分链表为空:比如
lists = [[1,3], [], [2,4]],分治后会将空链表当作nullptr处理,mergeTwoLists能正确合并nullptr和有效链表(直接返回有效链表)。
总结
该代码的核心优势:
- 分治思想降低时间复杂度,从暴力合并的 O (Nk) 优化到 O (N log k)。
- 代码结构清晰,职责划分明确(分治 + 两两合并),易于理解和维护。
- 边界处理完善,覆盖所有题目要求的特殊情况。
本质是 "归并排序" 在链表上的应用:拆分(分)→ 合并(治),是解决 "多有序序列合并" 问题的通用思路。
题目链接
题目描述
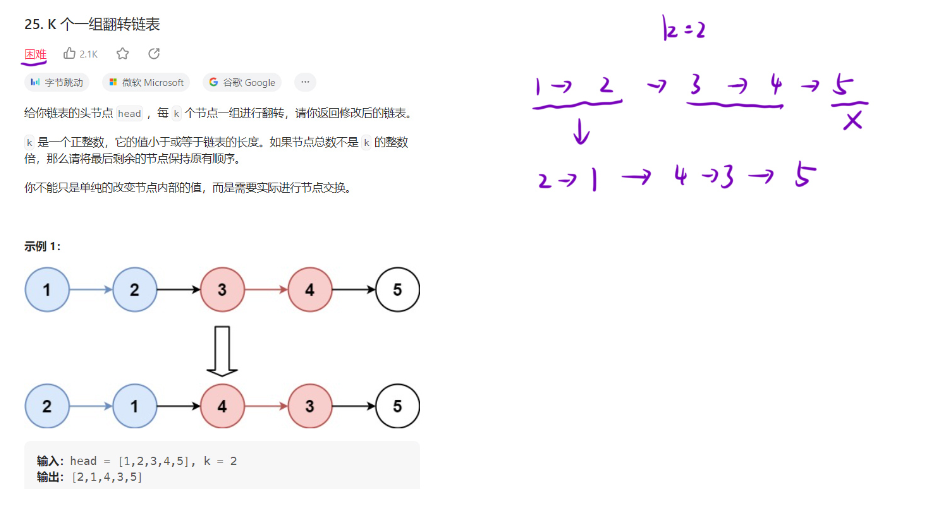
题目解析
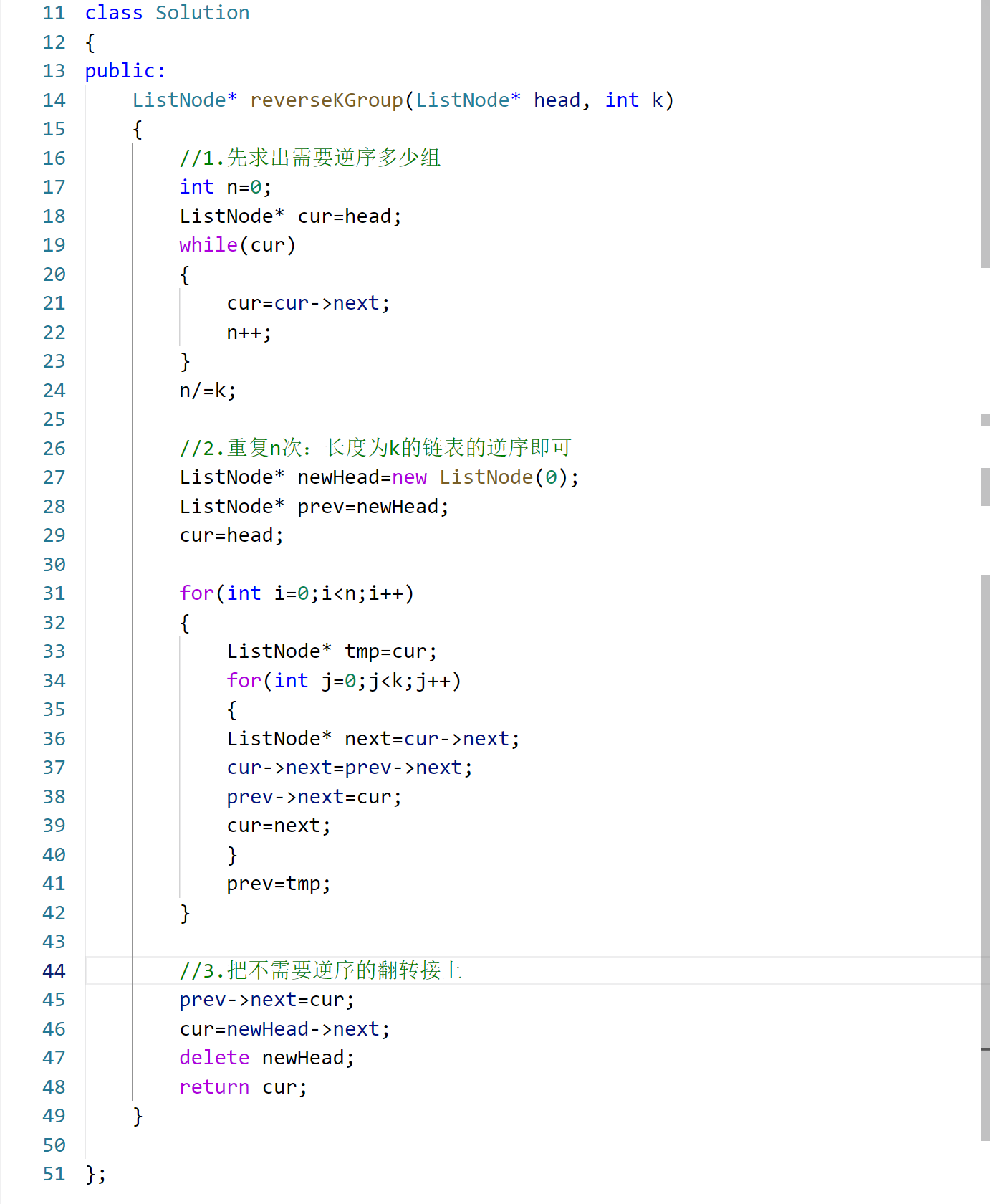
二、算法核心思路
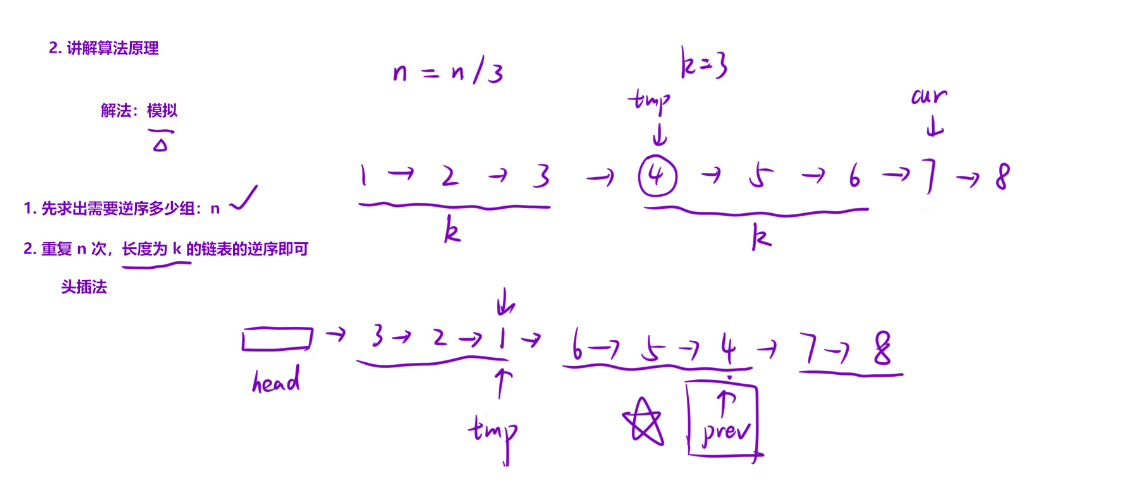
这个解法的核心是 「分组局部翻转 + 整体衔接」,步骤拆解:
- 统计分组数:先遍历链表计算总长度,确定能完整翻转的组数(总长度 ÷ k,向下取整);
- 局部翻转每组:对每个完整组,用「头插法」逆序(借助虚拟头节点简化衔接);
- 衔接剩余节点:最后一组翻转后,将剩余未翻转的节点接在链表尾部。
三、代码逐行拆解
1. 统计链表长度与分组数
cpp
int n = 0;
ListNode* cur = head;
while (cur) {
cur = cur->next;
n++;
}
n /= k; // 得到能完整翻转的组数(不足k个的组不翻转)- 作用:遍历链表统计总节点数
n,计算出需要翻转的组数(例如 n=5、k=2 时,组数 = 2); - 为什么要统计?避免对最后不足
k个节点的组进行翻转。
2. 初始化辅助指针(关键!)
cpp
ListNode* newHead = new ListNode(0); // 虚拟头节点(简化头节点处理)
ListNode* prev = newHead; // 指向「上一组翻转后的尾节点」(初始指向虚拟头)
cur = head; // 指向「当前组的第一个节点」(初始指向原链表头)- 虚拟头节点
newHead:链表翻转时,头节点会变化,用虚拟头统一处理(避免单独判断头节点); prev指针:核心衔接指针,始终指向「上一组翻转后的最后一个节点」,用于连接当前组翻转后的头节点;cur指针:用于遍历原链表,每次指向当前组的第一个节点。
3. 循环翻转每组(核心操作)
cpp
for (int i = 0; i < n; i++) { // 遍历n个需要翻转的组
ListNode* tmp = cur; // 保存当前组的第一个节点(翻转后会成为组尾)
for (int j = 0; j < k; j++) { // 对当前组的k个节点进行「头插法」翻转
ListNode* next = cur->next; // 暂存cur的下一个节点(避免断链)
cur->next = prev->next; // 步骤1:cur指向「prev的下一个节点」(即当前组已翻转部分的头)
prev->next = cur; // 步骤2:prev指向cur(将cur加入已翻转部分的头部)
cur = next; // 步骤3:cur移动到下一个待翻转节点
}
prev = tmp; // 本组翻转完成,prev更新为当前组的尾节点(即原组头)
}这部分是 局部翻转的核心 ,用「头插法」实现 k 个节点的逆序,我们用具体例子拆解(以第一组 1→2,k=2 为例):
初始状态(第一组开始):
prev = newHead(val=0,next=nullptr)cur = 1(当前组第一个节点)tmp = 1(保存组头,后续作为组尾)
第一次内层循环(j=0,处理节点 1):
next = cur->next = 2(暂存节点 2)cur->next = prev->next = nullptr(节点 1 指向 prev 的下一个,此时为空)prev->next = cur = 1(prev 的 next 指向 1,此时新链表:0→1)cur = next = 2(cur 移动到节点 2)
第二次内层循环(j=1,处理节点 2):
next = cur->next = 3(暂存节点 3,为下一组做准备)cur->next = prev->next = 1(节点 2 指向当前已翻转部分的头 1)prev->next = cur = 2(prev 的 next 指向 2,此时新链表:0→2→1)cur = next = 3(cur 移动到节点 3)
本组翻转完成:
- 第一组从
1→2变成2→1; prev = tmp = 1(prev 更新为当前组尾,用于连接下一组)。
下一组(节点 3→4)会重复上述过程,最终翻转成 4→3,且通过 prev=3(原组头)衔接。
4. 衔接剩余节点 + 清理虚拟头
cpp
prev->next = cur; // 最后一组翻转后,prev是组尾,cur指向剩余未翻转的节点(如示例中的5)
cur = newHead->next; // cur指向翻转后的真实头节点(跳过虚拟头)
delete newHead; // 释放虚拟头节点(避免内存泄漏)
return cur; // 返回结果- 剩余节点处理:当所有完整组翻转后,
cur指向最后不足 k 个节点的第一个(如示例中的 5),直接接在最后一组的尾节点prev后面; - 虚拟头清理:虚拟头只是辅助工具,最终要释放内存,返回真实头节点
newHead->next。
四、关键技巧总结
- 虚拟头节点:解决链表头节点翻转后变化的问题,统一所有组的衔接逻辑;
- 头插法:高效实现局部 k 个节点的逆序(时间复杂度 O (k) per 组,整体 O (n));
- 指针分工明确 :
cur:遍历原链表,指向当前待处理节点;prev:衔接各组,指向已处理部分的尾节点;tmp:保存当前组的原头节点(翻转后成为组尾);next:暂存下一个节点,避免链表断链。
五、时间与空间复杂度
- 时间复杂度:O (n),n 为链表总长度。遍历链表 2 次(1 次统计长度,1 次翻转所有节点),每组翻转 k 个节点的总操作数为 n;
- 空间复杂度:O (1),仅使用常数个辅助指针(无递归或额外数据结构)。