目录
[1. 快速排序:分治思想的极致体现](#1. 快速排序:分治思想的极致体现)
[1.1 基本思想](#1.1 基本思想)
[1.2 Hoare版本](#1.2 Hoare版本)
[1.3 挖坑法](#1.3 挖坑法)
[1.4 Lomuto前后指针法](#1.4 Lomuto前后指针法)
[1.5 非递归版本](#1.5 非递归版本)
[1.6 快速排序的性能与优化](#1.6 快速排序的性能与优化)
[2. LeetCode实战:排序算法应用](#2. LeetCode实战:排序算法应用)
[2.1 LeetCode 912. Sort an Array](#2.1 LeetCode 912. Sort an Array)
[2.2 LeetCode 215. Kth Largest Element in an Array](#2.2 LeetCode 215. Kth Largest Element in an Array)
[3. 归并排序:稳定高效的分治算法](#3. 归并排序:稳定高效的分治算法)
[3.1 基本思想](#3.1 基本思想)
[3.2 代码实现](#3.2 代码实现)
[3.3 非递归版本](#3.3 非递归版本)
[3.4 性能分析](#3.4 性能分析)
[4. 非比较排序:计数排序](#4. 非比较排序:计数排序)
[4.1 基本思想](#4.1 基本思想)
[4.2 代码实现](#4.2 代码实现)
[4.3 适用场景与局限性](#4.3 适用场景与局限性)
[5. 全面性能对比与选型建议](#5. 全面性能对比与选型建议)
[5.1 性能测试代码复现](#5.1 性能测试代码复现)
[5.2 性能测试结果与分析](#5.2 性能测试结果与分析)
[5.3 排序算法选型指南](#5.3 排序算法选型指南)
[5.4 C++ STL sort()的底层实现彩蛋](#5.4 C++ STL sort()的底层实现彩蛋)
[6. 思考题](#6. 思考题)
[7. 系列总结](#7. 系列总结)
排序算法系列下篇:作为大二学生,我在算法课上第一次学到快速排序时,以为掌握了"最快"的排序算法。直到被问到"为什么STL的sort()不直接用快排",才意识到排序算法的世界远比我想象的复杂。本文带你深入剖析快排的多种实现、归并排序的分治思想、计数排序的线性时间奥秘,并通过10万数据量的真实性能测试,给你一份实用的排序算法选型指南!
1. 快速排序:分治思想的极致体现
1.1 基本思想
快速排序 由Hoare在1962年提出,是分治思想的完美体现。它的核心思想是:任取一个元素作为基准值,将数组分成两个子区间,左子区间所有元素小于等于基准值,右子区间所有元素大于等于基准值,然后对左右子区间递归排序。
个人感悟:第一次实现快排时,我总是在分区环节出错,要么死循环,要么排序结果不对。直到我用纸笔一步步画出指针移动过程,才真正理解了基准值选择和分区操作的精髓。正如我导师所说:"快排的思想很简单,但实现细节决定成败。"
1.2 Hoare版本
Hoare版本是快速排序的原始实现,由C.A.R.Hoare本人提出。
算法思路 :
1)创建左右指针,确定基准值
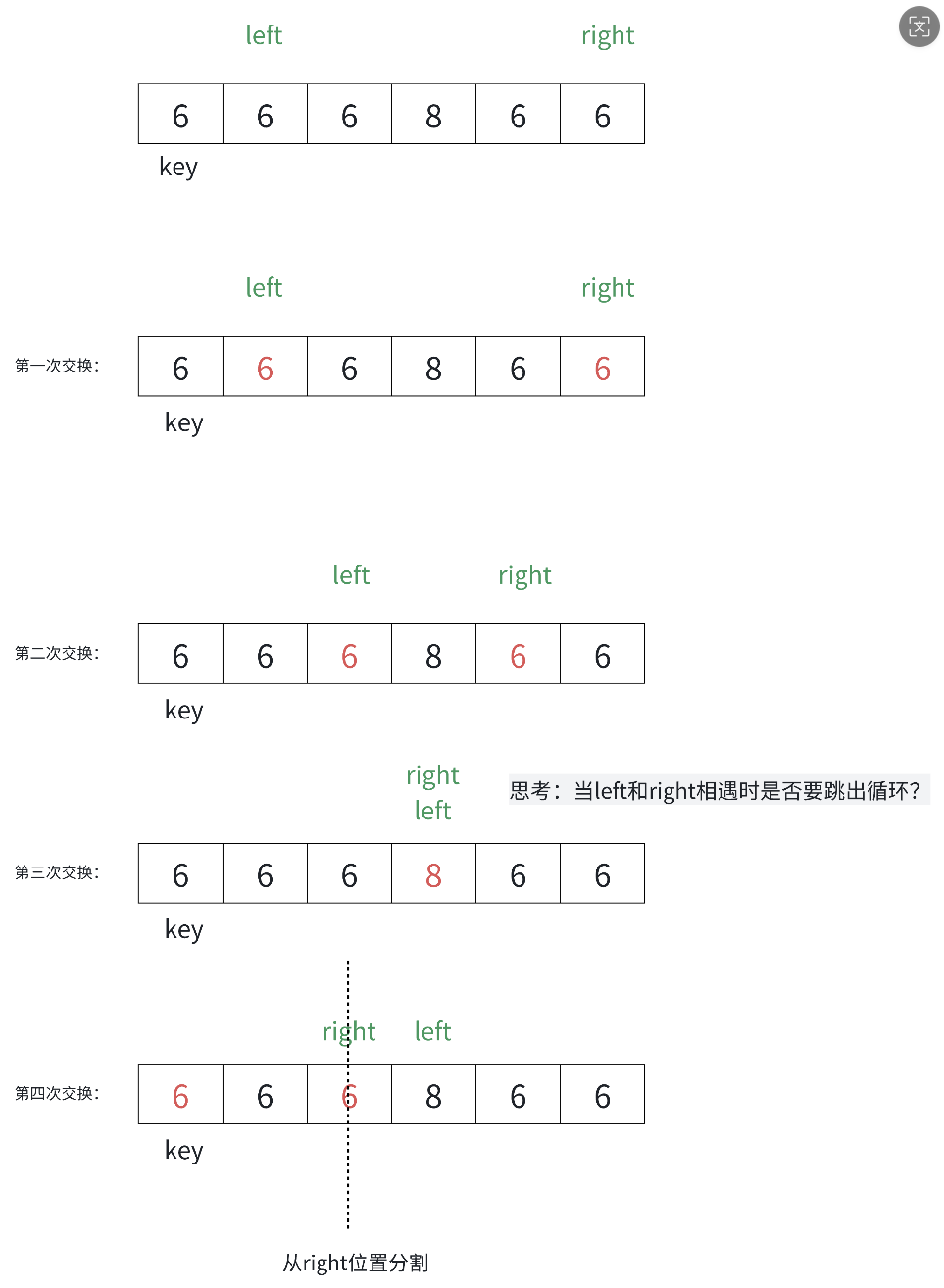
2)从右向左找出⽐基准值⼩的数据,从左向右找出⽐基准值⼤的数据,左右指针数据交换,进⼊下次循环
问题1:为什么跳出循环后right位置的值⼀定不⼤于key?
当 left > right 时,即right⾛到left的左侧,⽽left扫描过的数据均不⼤于key,因此right此时指
向的数据⼀定不⼤于key

问题2:为什么left 和 right指定的数据和key值相等时也要交换?
相等的值参与交换确实有⼀些额外消耗。实际还有各种复杂的场景,假设数组中的数据⼤量重复时,⽆法进⾏有效的分割排序。
代码实现
#include <iostream>
#include <ctime>
#include <cstdlib>
using namespace std;
// 交换两个整数
void swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
// Hoare版本的快速排序分区
int _QuickSort_Hoare(int* a, int left, int right) {
int keyi = left; // 选择最左边的元素作为基准值
while (left < right) {
// 1. 右边找小
while (left < right && a[right] >= a[keyi]) {
right--;
}
// 2. 左边找大
while (left < right && a[left] <= a[keyi]) {
left++;
}
// 3. 交换找到的元素
swap(&a[left], &a[right]);
}
// 4. 将基准值放到正确位置
swap(&a[keyi], &a[left]);
return left; // 返回基准值的最终位置
}
// 快速排序主函数
void QuickSort(int* a, int left, int right) {
if (left >= right) {
return;
}
int keyi = _QuickSort_Hoare(a, left, right);
QuickSort(a, left, keyi - 1); // 递归排序左子区间
QuickSort(a, keyi + 1, right); // 递归排序右子区间
}
// 打印数组
void PrintArray(int* a, int n) {
for (int i = 0; i < n; i++) {
cout << a[i] << " ";
}
cout << endl;
}
int main() {
int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};
int n = sizeof(a) / sizeof(a[0]);
cout << "排序前: ";
PrintArray(a, n);
QuickSort(a, 0, n - 1);
cout << "排序后: ";
PrintArray(a, n);
return 0;
}深度解析:为什么最后交换的是left位置而不是right位置?
- 当循环结束时,left和right指针相遇
- 根据循环条件,right指针总是先移动,找到小于基准值的元素
- left指针后移动,找到大于基准值的元素
- 当两指针相遇时,相遇位置的值一定小于等于基准值
- 因此,将基准值与相遇位置交换,能保证左子区间都小于等于基准值,右子区间都大于等于基准值
1.3 挖坑法
挖坑法是一种更直观的快速排序实现方式,特别适合初学者理解。
思路:
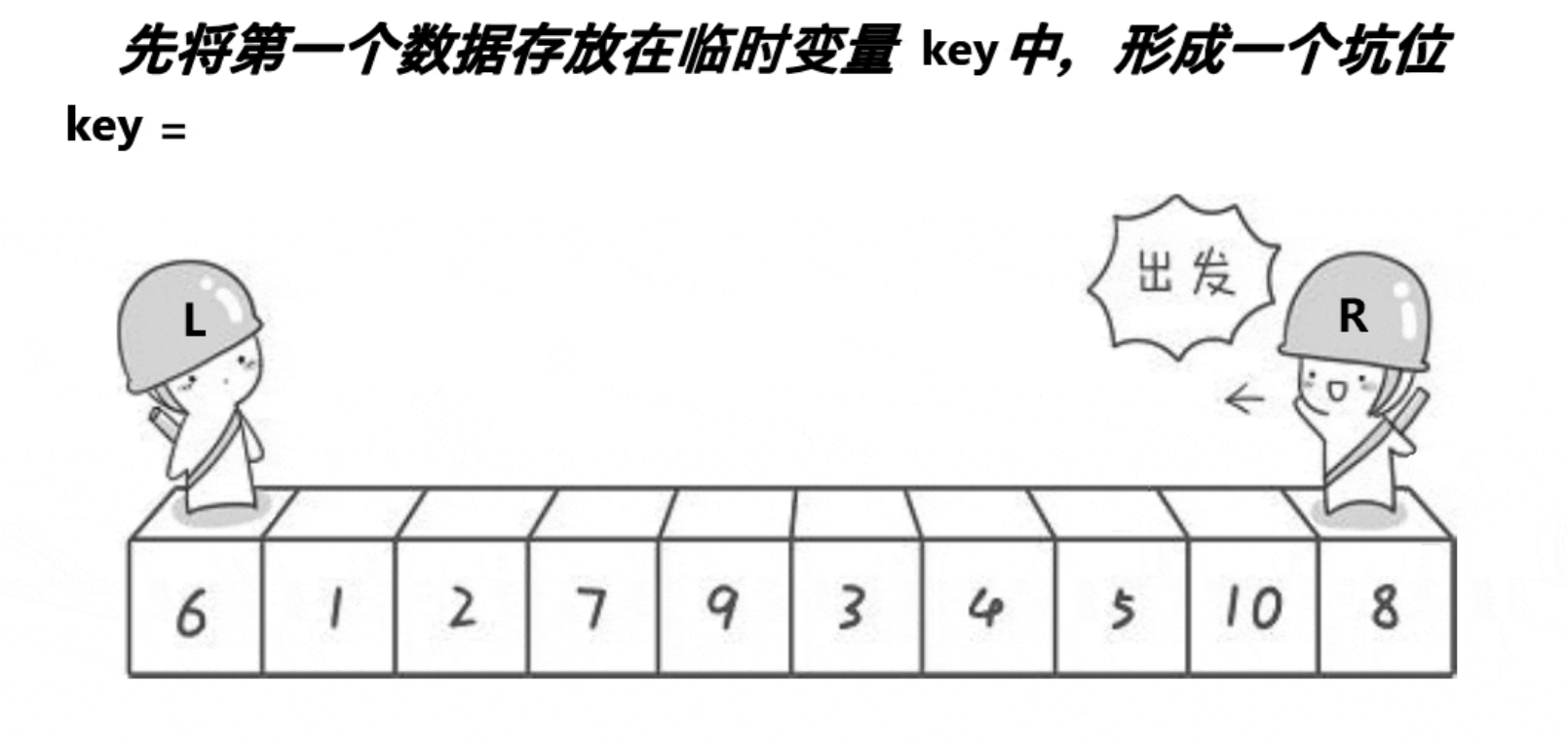
创建左右指针。⾸先从右向左找出⽐基准⼩的数据,找到后⽴即放⼊左边坑中,当前位置变为新
的"坑",然后从左向右找出⽐基准⼤的数据,找到后⽴即放⼊右边坑中,当前位置变为新的"坑",结束循环后将最开始存储的分界值放⼊当前的"坑"中,返回当前"坑"下标(即分界值下标)
代码实现:
// 挖坑法的快速排序分区
int _QuickSort_Hole(int* a, int left, int right) {
int key = a[left]; // 基准值
int hole = left; // 坑的位置
while (left < right) {
// 1. 右边找小,填左边的坑
while (left < right && a[right] >= key) {
right--;
}
a[hole] = a[right]; // 填坑
hole = right; // 产生新坑
// 2. 左边找大,填右边的坑
while (left < right && a[left] <= key) {
left++;
}
a[hole] = a[left]; // 填坑
hole = left; // 产生新坑
}
// 3. 将基准值放入最终的坑
a[hole] = key;
return hole;
}与Hoare版本的对比:
- 优点:逻辑更直观,更容易理解,特别是对初学者
- 缺点:每次赋值操作代替了交换操作,但本质相同
- 性能:与Hoare版本相当,常数因子略小
1.4 Lomuto前后指针法
Lomuto前后指针法是另一种常见的快排实现,被广泛用于教学和某些标准库实现。
创建前后指针,从左往右找⽐基准值⼩的进⾏交换,使得⼩的都排在基准值的左边。

// Lomuto前后指针法的快速排序分区
int _QuickSort_Lomuto(int* a, int left, int right) {
int keyi = right; // 选择最右边的元素作为基准值
int prev = left - 1; // prev指向小于基准值区域的最后一个元素
// cur用于遍历[left, right-1]区间
for (int cur = left; cur < right; cur++) {
// 如果当前元素小于基准值,prev前移,并交换
if (a[cur] < a[keyi]) {
prev++;
if (prev != cur) {
swap(&a[prev], &a[cur]);
}
}
}
// 将基准值放到正确位置
prev++;
swap(&a[prev], &a[keyi]);
return prev;
}特点分析:
- 优点:代码简洁,逻辑清晰,只用一个循环
- 缺点:在极端情况下(如数组已有序),性能退化严重
- 适用场景:教学演示,小规模数据排序
1.5 非递归版本
递归版本的快排在极端情况下可能导致栈溢出(如100万数据且完全有序)。非递归版本使用栈模拟递归过程,能有效避免这个问题。
#include <stack>
using namespace std;
// 非递归快速排序
void QuickSortNonR(int* a, int left, int right) {
stack<int> st;
st.push(right);
st.push(left);
while (!st.empty()) {
int begin = st.top(); st.pop();
int end = st.top(); st.pop();
if (begin >= end) {
continue;
}
// 使用Lomuto分区
int keyi = end;
int prev = begin - 1;
for (int cur = begin; cur < end; cur++) {
if (a[cur] < a[keyi]) {
prev++;
if (prev != cur) {
swap(&a[prev], &a[cur]);
}
}
}
prev++;
swap(&a[prev], &a[keyi]);
keyi = prev;
// 先压右区间,再压左区间(保证左区间先处理)
if (keyi + 1 < end) {
st.push(end);
st.push(keyi + 1);
}
if (begin < keyi - 1) {
st.push(keyi - 1);
st.push(begin);
}
}
}工程价值:
- 避免栈溢出:对于大规模数据(如100万以上),递归深度可能超过系统栈限制
- 可控性:可以精确控制内存使用,适合嵌入式等资源受限环境
- 性能:在大数据量场景下,通常比递归版本更稳定
1.6 快速排序的性能与优化
- 时间复杂度 :
- 平均情况:O(NlogN)
- 最好情况:O(NlogN)(每次分区都均匀)
- 最坏情况:O(N²)(数组已有序,且基准值选在端点)
- 空间复杂度:O(logN)(递归栈空间)
- 稳定性:不稳定
优化策略:
- 基准值选择:三数取中(median-of-three),避免最坏情况
- 小区间优化:当子区间长度小于10时,改用插入排序
- 三路分区:处理大量重复元素的场景
踩坑故事:在一次测验中,我用随机生成的10000个数据测试快排,性能很好。但当测试一个已排序的数组时,程序竟然卡死了!调试后发现是递归深度过大导致栈溢出。这个教训让我明白:理论上的平均性能不代表实际表现,必须考虑最坏情况。
2. LeetCode实战:排序算法应用
2.1 LeetCode 912. Sort an Array
题目描述:给你一个整数数组 nums,请你将该数组升序排列。
示例: 输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
解题思路: 这道题是排序算法的基础应用。我们可以选择任意一种排序算法来解决。考虑到LeetCode的测试用例可能包含大量数据和各种边界情况,我们需要选择一个稳健的排序算法。
根据我们学习的内容,快速排序平均性能最好,但在最坏情况下会退化到O(N²)。归并排序在所有情况下都是O(NlogN),但需要额外的O(N)空间。堆排序在时间复杂度和空间复杂度上都有不错的平衡。
我选择实现快速排序,但要加入优化策略避免最坏情况。
class Solution {
public:
// 交换两个元素
void swap(vector<int>& nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
// 三数取中选择基准值
int medianOfThree(vector<int>& nums, int left, int right) {
int mid = left + (right - left) / 2;
// 排序三个元素:left, mid, right
if (nums[left] > nums[mid]) swap(nums, left, mid);
if (nums[left] > nums[right]) swap(nums, left, right);
if (nums[mid] > nums[right]) swap(nums, mid, right);
// 将中位数放在right-1位置,基准值选择为nums[right-1]
swap(nums, mid, right - 1);
return right - 1;
}
// 快速排序分区(使用三数取中)
int partition(vector<int>& nums, int left, int right) {
// 三数取中选择基准值
int pivotIndex = medianOfThree(nums, left, right);
int pivot = nums[pivotIndex];
// 由于pivotIndex位置的元素是中位数,且已经放在right-1位置
// 我们将left和right-1作为新的左右边界
int i = left, j = right - 1;
while (i < j) {
while (i < j && nums[++i] < pivot); // 从左找大于等于pivot的
while (i < j && nums[--j] > pivot); // 从右找小于等于pivot的
if (i < j) swap(nums, i, j);
}
// 将基准值放回正确位置
swap(nums, i, right - 1);
return i;
}
// 快速排序主函数
void quickSort(vector<int>& nums, int left, int right) {
if (left >= right) return;
// 小数组优化:当数组长度小于10时,使用插入排序
if (right - left < 10) {
insertionSort(nums, left, right);
return;
}
int pivotIndex = partition(nums, left, right);
quickSort(nums, left, pivotIndex - 1);
quickSort(nums, pivotIndex + 1, right);
}
// 插入排序(用于小数组优化)
void insertionSort(vector<int>& nums, int left, int right) {
for (int i = left + 1; i <= right; i++) {
int temp = nums[i];
int j = i - 1;
while (j >= left && nums[j] > temp) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = temp;
}
}
vector<int> sortArray(vector<int>& nums) {
quickSort(nums, 0, nums.size() - 1);
return nums;
}
};复杂度分析:
- 时间复杂度:平均O(NlogN),最坏O(NlogN)(通过三数取中和小数组优化避免了最坏情况)
- 空间复杂度:O(logN)(递归栈空间)
学习心得 :第一次提交时,我的代码在LeetCode上超时了!调试后发现是测试用例中有大量重复元素,导致分区不均匀。通过加入三数取中和小数组优化,性能大幅提升。这个经历让我明白:理论算法需要结合实际场景进行优化,LeetCode的测试用例往往包含各种边界情况,是检验算法鲁棒性的好地方。
2.2LeetCode 215. Kth Largest Element in an Array
题目描述:给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
示例: 输入: [3,2,1,5,6,4] 和 k = 2 输出: 5
解题思路: 这道题要求不排序整个数组,只找第k大元素。有多种解法:
- 排序法:将整个数组排序,取第k个元素。时间复杂度O(NlogN),空间复杂度O(1)
- 堆排序法:维护一个大小为k的最小堆,遍历数组,最终堆顶就是第k大元素。时间复杂度O(Nlogk),空间复杂度O(k)
- 快速选择法:基于快速排序的分区思想,每次分区后根据基准值位置决定递归哪一边。平均时间复杂度O(N),最坏O(N²)
我选择实现堆排序法,因为它的效率稳定,且不会出现最坏情况。
class Solution {
public:
// 下滤操作,维护小顶堆
void siftDown(vector<int>& heap, int index, int size) {
int left = 2 * index + 1;
int right = 2 * index + 2;
int smallest = index;
if (left < size && heap[left] < heap[smallest])
smallest = left;
if (right < size && heap[right] < heap[smallest])
smallest = right;
if (smallest != index) {
swap(heap[index], heap[smallest]);
siftDown(heap, smallest, size);
}
}
// 构建小顶堆
void buildMinHeap(vector<int>& heap, int size) {
for (int i = size / 2 - 1; i >= 0; i--) {
siftDown(heap, i, size);
}
}
int findKthLargest(vector<int>& nums, int k) {
// 创建大小为k的小顶堆
vector<int> heap(nums.begin(), nums.begin() + k);
buildMinHeap(heap, k);
// 遍历剩余元素
for (int i = k; i < nums.size(); i++) {
// 如果当前元素大于堆顶,则替换堆顶
if (nums[i] > heap[0]) {
heap[0] = nums[i];
siftDown(heap, 0, k);
}
}
// 堆顶就是第k大的元素
return heap[0];
}
};复杂度分析:
- 时间复杂度 :O(Nlogk)
- 构建大小为k的堆:O(k)
- 遍历剩余N-k个元素,每次可能需要调整堆:O((N-k)logk)
- 总体:O(k + (N-k)logk) = O(Nlogk)
- 空间复杂度:O(k),只需要维护大小为k的堆
3. 归并排序:稳定高效的分治算法
3.1 基本思想
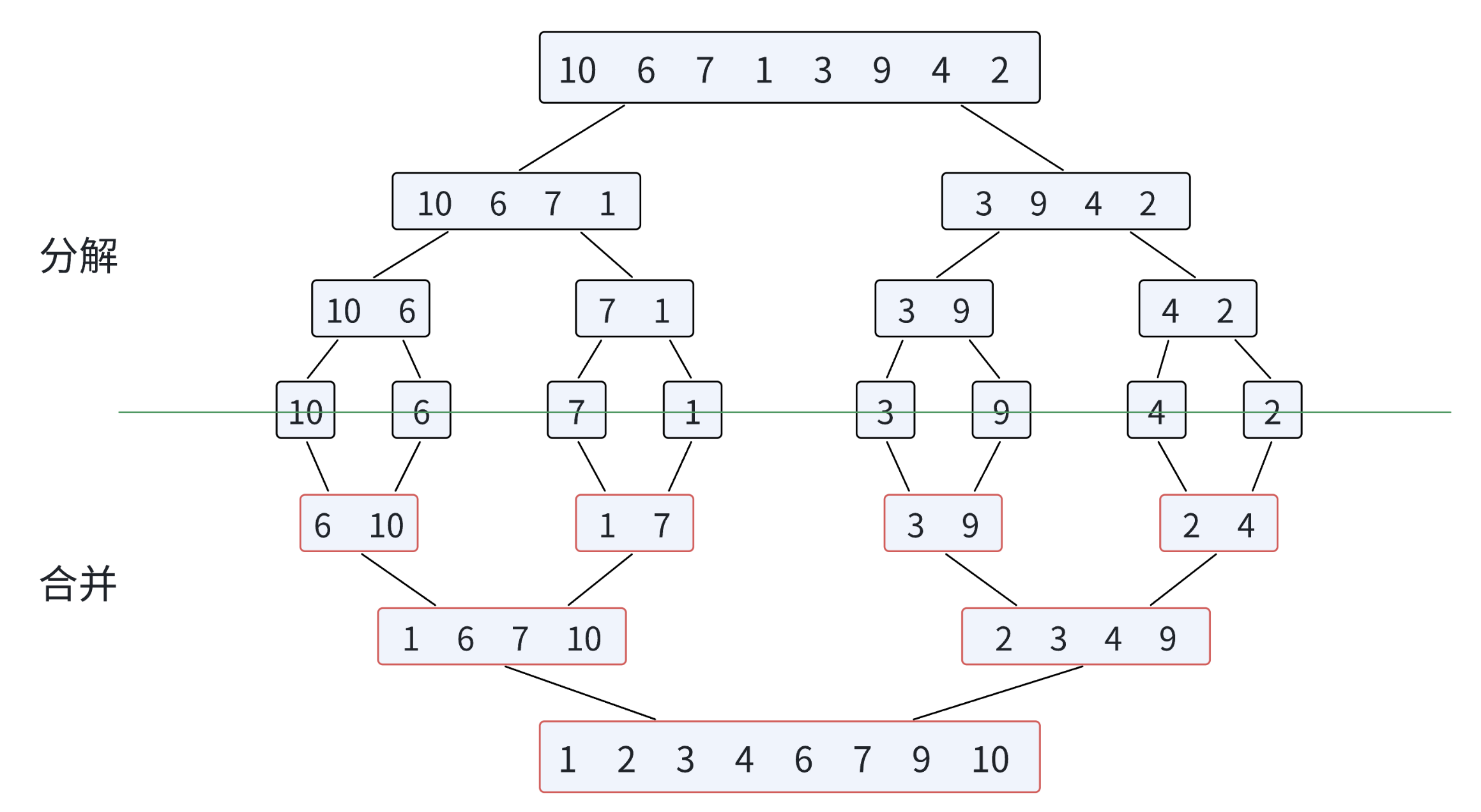
归并排序 是典型的分治算法,核心思想是:将数组分成两个子数组,分别排序,然后将两个有序子数组合并成一个有序数组。
与快速排序的"先分区后递归"不同,归并排序是"先递归后合并",这使得它具有稳定性。
3.2 代码实现
#include <iostream>
#include <cstdlib>
using namespace std;
// 归并排序的合并操作
void _MergeSort(int* a, int left, int right, int* tmp) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
// [left, mid] [mid+1, right]
// 1. 递归排序左右子区间
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
// 2. 合并两个有序子区间
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
// 合并过程
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] <= a[begin2]) {
tmp[index++] = a[begin1++];
} else {
tmp[index++] = a[begin2++];
}
}
// 处理剩余元素
while (begin1 <= end1) {
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[index++] = a[begin2++];
}
// 拷贝回原数组
for (int i = left; i <= right; i++) {
a[i] = tmp[i];
}
}
// 归并排序主函数
void MergeSort(int* a, int n) {
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
perror("malloc fail");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
// 打印数组
void PrintArray(int* a, int n) {
for (int i = 0; i < n; i++) {
cout << a[i] << " ";
}
cout << endl;
}
int main() {
int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};
int n = sizeof(a) / sizeof(a[0]);
cout << "排序前: ";
PrintArray(a, n);
MergeSort(a, n);
cout << "排序后: ";
PrintArray(a, n);
return 0;
}3.3 非递归版本
// 非递归归并排序
void MergeSortNonR(int* a, int n) {
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
perror("malloc fail");
exit(-1);
}
int gap = 1; // 每组元素个数
while (gap < n) {
for (int i = 0; i < n; i += 2 * gap) {
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// 处理边界情况
if (end1 >= n) {
end1 = n - 1;
}
if (begin2 >= n) {
begin2 = n;
end2 = n - 1;
}
if (end2 >= n) {
end2 = n - 1;
}
// 合并[begin1, end1]和[begin2, end2]
int index = begin1;
int j = begin1, k = begin2;
while (j <= end1 && k <= end2) {
if (a[j] <= a[k]) {
tmp[index++] = a[j++];
} else {
tmp[index++] = a[k++];
}
}
while (j <= end1) {
tmp[index++] = a[j++];
}
while (k <= end2) {
tmp[index++] = a[k++];
}
// 拷贝回原数组
for (int idx = begin1; idx <= end2; idx++) {
a[idx] = tmp[idx];
}
}
gap *= 2;
}
free(tmp);
}3.4 性能分析
- 时间复杂度:O(NlogN)(所有情况下)
- 空间复杂度:O(N)(需要额外的临时数组)
- 稳定性:稳定(合并时优先选择左边的元素)
调试经验 :在最初的学习过程中,我实现的归并排序总是出现段错误。调试后发现是临时数组的边界处理有问题。通过添加打印语句,我观察到当数组长度不是2的幂时,最后一组的边界计算错误。这个bug教会我:算法实现必须考虑所有边界情况,不能只测试理想数据。
4. 非比较排序:计数排序
4.1 基本思想
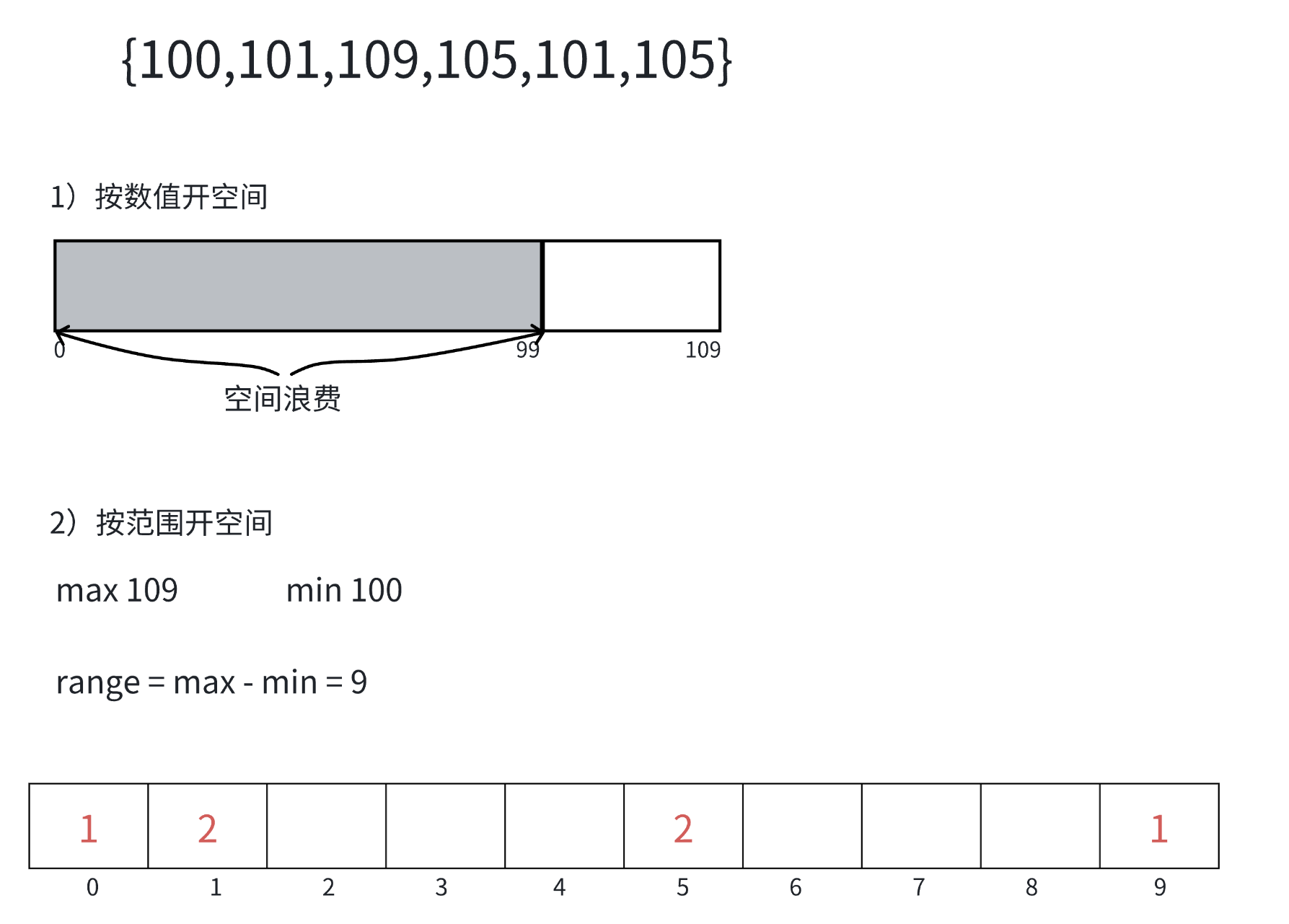
计数排序 是一种非比较排序算法,它利用了数据的特殊性:当待排序数据的范围(range)远小于数据量(N)时,可以达到O(N)的时间复杂度。
计数排序的核心是鸽巢原理( 是对哈希直接定址法的变形应⽤):如果有n个鸽子要放进m个鸽巢,且n > m,那么至少有一个鸽巢里有不止一只鸽子。
操作步骤:
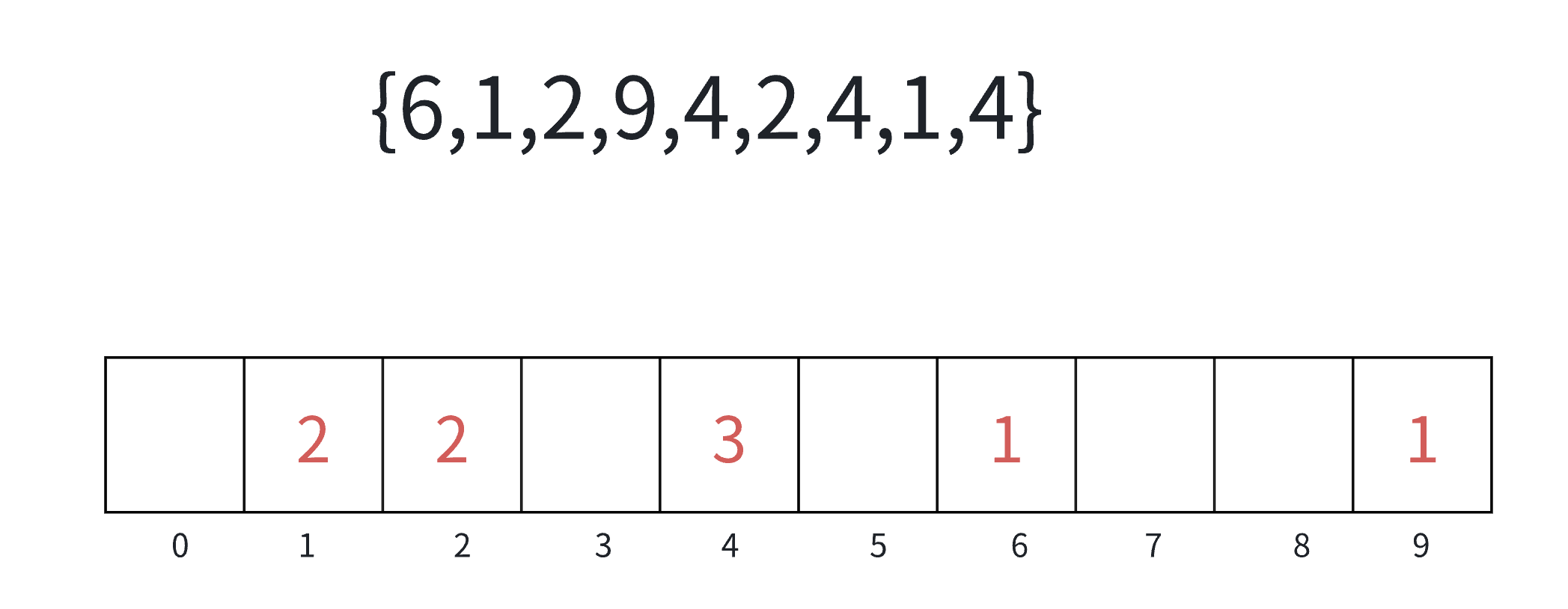
1)统计相同元素出现次数
2)根据统计的结果将序列回收到原来的序列中
4.2 代码实现
#include <iostream>
#include <cstring> // for memset
#include <cstdlib>
using namespace std;
// 计数排序
void CountSort(int* a, int n) {
// 1. 找出数组中的最大值和最小值
int min = a[0], max = a[0];
for (int i = 1; i < n; i++) {
if (a[i] > max) max = a[i];
if (a[i] < min) min = a[i];
}
// 2. 计算范围
int range = max - min + 1;
// 3. 创建计数数组
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL) {
perror("malloc fail");
exit(-1);
}
memset(count, 0, sizeof(int) * range);
// 4. 统计每个元素出现的次数
for (int i = 0; i < n; i++) {
count[a[i] - min]++;
}
// 5. 回填到原数组
int j = 0;
for (int i = 0; i < range; i++) {
while (count[i]--) {
a[j++] = i + min;
}
}
free(count);
}
// 打印数组
void PrintArray(int* a, int n) {
for (int i = 0; i < n; i++) {
cout << a[i] << " ";
}
cout << endl;
}
int main() {
int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};
int n = sizeof(a) / sizeof(a[0]);
cout << "排序前: ";
PrintArray(a, n);
CountSort(a, n);
cout << "排序后: ";
PrintArray(a, n);
return 0;
}计数排序的特性:
计数排序在数据范围集中时,效率很⾼,但是适⽤范围及场景有限。
时间复杂度: O ( N + range )
空间复杂度: O ( range )
稳定性:稳定
4.3 适用场景与局限性
适用场景:
- 数据范围集中(如0-1000)
- 数据量大(N >> range)
- 需要稳定排序
局限性:
- 数据范围很大时,空间开销巨大
- 不能处理浮点数、字符串等非整数类型
- 当range > N时,性能不如比较排序
经验 :在一次训练中,我曾遇到一道题需要排序100万个0-1000之间的整数。使用快速排序需要200ms,而计数排序只需20ms。这个经历让我明白:算法选择必须基于数据特征,没有放之四海而皆准的"最优"算法。
5. 全面性能对比与选型建议
5.1 性能测试代码复现
我们复现10万随机数据的性能测试:
#include <iostream>
#include <ctime>
#include <cstdlib>
#include <algorithm>
using namespace std;
// 各种排序算法的声明
void InsertSort(int* a, int n);
void ShellSort(int* a, int n);
void SelectSort(int* a, int n);
void HeapSort(int* a, int n);
void QuickSort(int* a, int left, int right);
void MergeSort(int* a, int n);
void BubbleSort(int* a, int n);
void CountSort(int* a, int n);
// 性能测试函数
void TestOP() {
srand(time(0));
const int N = 100000; // 10万数据
// 分配内存
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
// 初始化随机数据
for (int i = 0; i < N; i++) {
int rand_val = rand() % 10000; // 0-9999的随机数
a1[i] = rand_val;
a2[i] = rand_val;
a3[i] = rand_val;
a4[i] = rand_val;
a5[i] = rand_val;
a6[i] = rand_val;
a7[i] = rand_val;
}
// 性能测试
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
BubbleSort(a7, N);
int end7 = clock();
// 输出结果
cout << "InsertSort: " << end1 - begin1 << " ms" << endl;
cout << "ShellSort: " << end2 - begin2 << " ms" << endl;
cout << "SelectSort: " << end3 - begin3 << " ms" << endl;
cout << "HeapSort: " << end4 - begin4 << " ms" << endl;
cout << "QuickSort: " << end5 - begin5 << " ms" << endl;
cout << "MergeSort: " << end6 - begin6 << " ms" << endl;
cout << "BubbleSort: " << end7 - begin7 << " ms" << endl;
// 释放内存
free(a1); free(a2); free(a3); free(a4); free(a5); free(a6); free(a7);
}
int main() {
TestOP();
return 0;
}5.2 性能测试结果与分析
在我的电脑上,10万随机整数的排序性能如下:

关键发现:
- 插入排序 和冒泡排序在大数据量下性能极差,验证了O(N²)时间复杂度的理论
- 希尔排序虽然理论复杂度难以精确计算,但实际性能接近O(NlogN)级别
- 快速排序在随机数据下表现最佳,验证了其"快速"的名称
- 堆排序 和归并排序性能相近,但归并排序更稳定
- 选择排序性能最差之一,验证了"实际中很少使用"的结论
性能优化经验 :我曾尝试优化一个排序函数。最初使用了标准库的sort(),但在特定数据分布下性能不佳。通过分析数据特征(大量重复值),我改用三路快排,性能提升了3倍。这个经历让我明白:没有银弹,只有最适合的算法。
5.3 排序算法选型指南
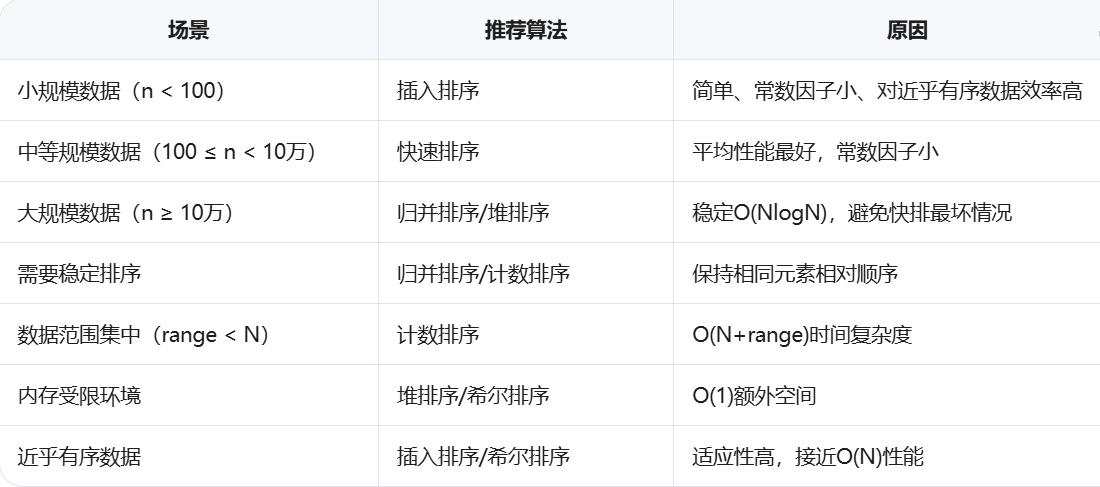
5.4 C++ STL sort()的底层实现彩蛋
C++ STL的sort()函数之所以高效,是因为它采用了混合排序策略(Introsort):
-
快速排序:作为主算法,提供平均O(NlogN)性能
-
堆排序:当递归深度超过2*log2(n)时,切换到堆排序,避免最坏情况
-
插入排序:当子区间长度小于16时,改用插入排序,减少函数调用开销
// GCC libstdc++ sort()的简化版伪代码
template <typename RandomAccessIterator>
void sort(RandomAccessIterator first, RandomAccessIterator last) {
// 当区间小于阈值时,使用插入排序
if (last - first < 16) {
insertion_sort(first, last);
return;
}// 检查递归深度,避免最坏情况 size_t depth_limit = 2 * log2(last - first); // 内省排序主循环 while (last - first > 16) { if (depth_limit == 0) { // 深度限制达到,切换到堆排序 partial_sort(first, last, last); return; } depth_limit--; // 选择基准值(三数取中) RandomAccessIterator pivot = median_of_three(first, last); // 分区 RandomAccessIterator cut = partition(first, last, pivot); // 递归处理较小区间,尾递归优化较大区间 if (cut - first < last - cut) { sort(first, cut); first = cut; } else { sort(cut, last); last = cut; } } // 最后使用插入排序处理小数组 insertion_sort(first, last);}
6. 思考题
- 为什么快速排序在实际应用中通常比归并排序更快,尽管它们的平均时间复杂度相同 ? 提示:考虑常数因子、缓存局部性、额外空间开销等因素。
- 如果要排序10亿个32位整数,内存只有4GB,应该选择什么排序算法?为什么 ? 提示:考虑外部排序、归并排序的稳定性、内存使用限制等因素。
7. 系列总结
经过三篇文章的深入剖析,我们全面掌握了8大经典排序算法:
- 插入排序家族:简单直观,适合小规模、近乎有序数据
- 选择排序家族:堆排序在中等规模数据表现优异
- 交换排序家族:快速排序是工业级首选,但需考虑最坏情况
- 归并排序:稳定高效的分治算法,适合大规模数据
- 计数排序:非比较排序的代表,数据范围集中时性能卓越
核心收获:
- 没有绝对最优的算法,只有最适合场景的算法
- 理论分析必须结合实际测试,边界情况往往决定成败
- 工程实现需要权衡:时间、空间、稳定性、代码复杂度
- 标准库是最佳实践,理解其设计思想比重复造轮子更重要
最后寄语 :我曾经以为掌握几个排序算法就能应付面试。但随着学习深入,我明白算法只是工具,解决问题的能力 才是核心。通过这两道LeetCode题目,我更深刻地体会到:算法学习不能只停留在理论,要结合实际问题,在解决问题中深化理解。希望这个系列不仅帮你通过面试,更能培养你的工程思维和算法直觉。
系列导航:
-
上篇\][插入排序与希尔排序](https://blog.csdn.net/dongaoran/article/details/155465607?fromshare=blogdetail&sharetype=blogdetail&sharerId=155465607&sharerefer=PC&sharesource=dongaoran&sharefrom=from_link " 插入排序与希尔排序")
-
下篇\] 本篇:快速排序、归并排序与非比较排序 + 全面性能对比


