目录
[3.Smooth L1](#3.Smooth L1)
摘要
本篇文章继续学习尚硅谷深度学习教程,学习内容是损失函数相关公式及适用场景和特性。
1.常见损失函数
1.均方误差(MSE)
均方误差(Mean Squared Error ,MSE),也称L2 Loss,常用于回归问题:
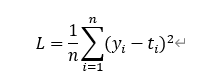
其中,yi表示神经网络的输出,ti表示监督数据的标签(正确的解标签),n则是数据的"维度"。对于固定维度的网络,前面的系数n不重要,因此公式有时也可以写成:
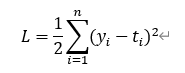
L2 Loss对异常值敏感,遇到异常值时易发生梯度爆炸。
代码如下:
python
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)2.交叉熵误差
除均方误差之外,交叉熵误差(Cross Entropy Error)也经常被用作损失函数,常用于分类问题
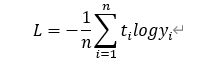
其中,log表示自然对数,yi表示神经网络的输出,ti表示正确解标签;而且,ti中只有正确解标签对应的值为1,其它均为0(one-hot表示)。
代码如下
python
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot向量的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size2.分类任务损失函数
1.二分类任务
二分类任务常用二元交叉熵损失函数(Binary Cross-Entropy Loss)
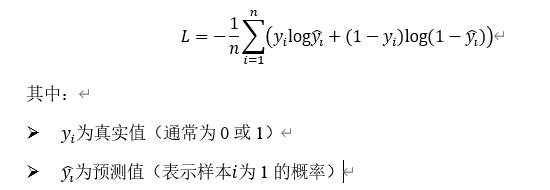
公式本身与交叉熵相似,只会取一项进行运算,一项系数为1,另一项系数为0。
2.多分类任务损失函数
多分类任务常用多类交叉熵损失函数(Categorical Cross-Entropy Loss)。它是对每个类别的预测概率与真实标签之间差异的加权平均。

3.回归任务损失函数
1.MAE
平均绝对误差(Mean Absolute Erro,MAE),也称L1 Loss:
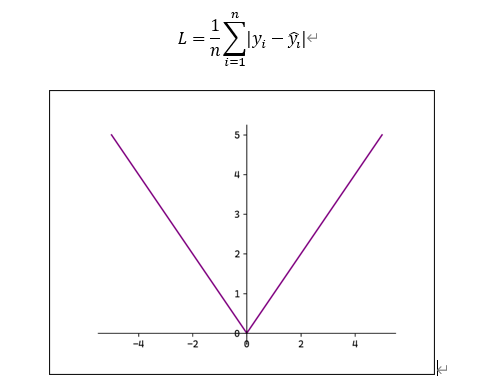
L1 Loss对异常值稳定,但在0点处不可导。
2.MSE
均方误差(Mean Squared Error ,MSE),也称L2 Loss:
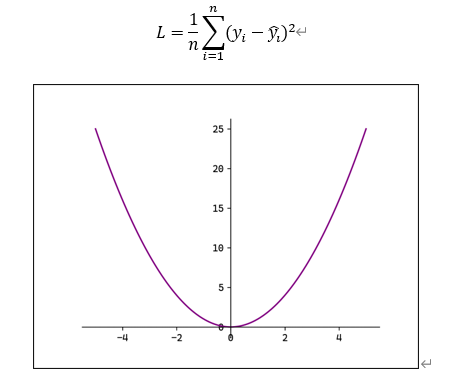
L2 Loss对异常值敏感,遇到异常值时易发生梯度爆炸。
3.Smooth L1
平滑L1:
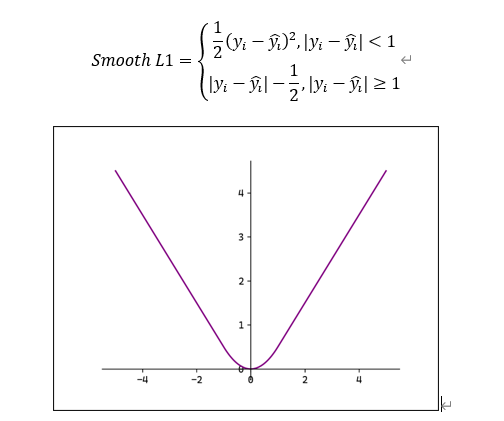
当误差较小时 使用L2 Loss,使得损失函数平滑可导。当误差较大时
使用L1 Loss降低异常值的影响。