锋哥原创的Transformer 大语言模型(LLM)基石视频教程:
https://www.bilibili.com/video/BV1X92pBqEhV
课程介绍

本课程主要讲解Transformer简介,Transformer架构介绍,Transformer架构详解,包括输入层,位置编码,多头注意力机制,前馈神经网络,编码器层,解码器层,输出层,以及Transformer Pytorch2内置实现,Transformer基于PyTorch2手写实现等知识。
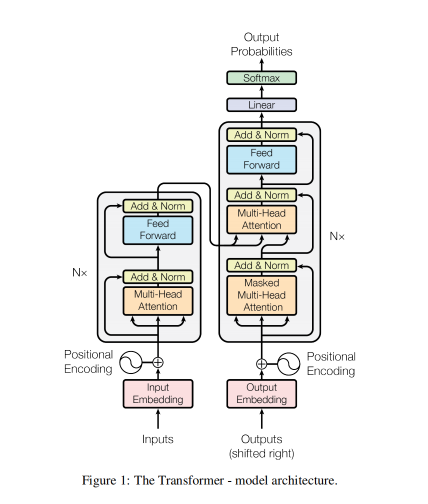
Transformer 大语言模型(LLM)基石 - Transformer架构详解 - 位置编码(Positional Encoding)详解与算法实现
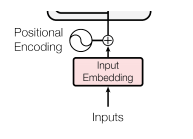
由于Transformer不具有像RNN或LSTM那样的时间步长顺序结构,它需要一个方法来注入序列中元素的位置信息。位置编码是将每个词语在序列中的位置表示为一个向量,与输入嵌入相加。
-
功能:向模型提供词语的位置信息,使得Transformer能够理解词语在序列中的相对位置。
-
结构:位置编码向量与输入嵌入矩阵逐元素相加,形状保持不变,仍为[batch_size, seq_len, embedding_dim]。
偶数位置用正弦函数,奇数位置用余弦函数。

公式参数:pos 是 词位置索引 dmodel是词嵌入维度
Transformer 中使用正弦和余弦函数进行位置编码,主要基于以下几个原因:
-
相对位置信息:正弦和余弦函数具有周期性,能够自然地表示相对位置。对于任意固定的偏移量 k,位置 pos+k 的位置编码可以表示为位置 pos 的位置编码的线性函数。这意味着模型可以很容易地学习到相对位置信息。
-
距离感知:正弦和余弦函数的乘积(内积)可以反映位置之间的距离。两个位置编码的内积会随着位置距离的增加而减少,这有助于模型捕捉序列中的顺序和距离。
-
唯一性:不同位置的正弦和余弦组合是唯一的,确保了每个位置都有唯一的编码。
-
连续性和平滑性:正弦和余弦函数是连续且平滑的,这有助于模型在训练过程中稳定地学习位置信息。
-
可扩展性:正弦和余弦函数可以处理任意长度的序列,因为它们的值域在 [-1, 1] 之间,不会随着位置增大而爆炸或消失。
代码实现:
import math
import torch
from torch import nn
# 输入嵌入层类
class Embeddings(nn.Module):
def __init__(self, vocab_size, embedding_dim): # vocab_size:词表大小 embedding_dim:词嵌入维度的大小
super().__init__()
self.embedding_dim = embedding_dim
self.embedding = nn.Embedding(vocab_size, embedding_dim)
def forward(self, x):
embed = self.embedding(x)
# 缩放词嵌入(原始Transformer论文中的关键细节) 防止向量初始值过大,稳定训练
return embed * math.sqrt(self.embedding_dim)
# 位置编码器层类
class PositionalEncoding(nn.Module):
"""
参数:
d_model: 嵌入维度(必须为偶数)
max_len: 支持的最大序列长度 也就是样本句子的最大长度
dropout: Dropout概率 防止模型过拟合,从而提升其泛化能力
"""
def __init__(self, d_model, max_len=100, dropout=0.1):
super().__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个二维张量,用于存储位置编码 [max_len, d_model]->[100, 512]
self.pe = torch.zeros(max_len, d_model)
print("pe:", self.pe)
print("pe.shape:", self.pe.shape)
# 创建一个二维张量,用于存储位置索引 [max_len, 1] -> [100, 1]
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
print(torch.arange(0, max_len, dtype=torch.float))
print("position:", position)
print("position.shape:", position.shape)
# 创建一个二维张量,用于存储位置编码的 sin 和 cos 值 维度: [d_model/2]
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
print("div_term:", div_term)
print("div_term.shape:", div_term.shape)
# 填充正弦和余弦值 position * div_term [100,256]
self.pe[:, 0::2] = torch.sin(position * div_term) # 偶数位置的 sin
self.pe[:, 1::2] = torch.cos(position * div_term) # 奇数位置的 cos
print("pe:", self.pe)
print("pe.shape:", self.pe.shape)
# 添加批次维度: [1, max_len, d_model] -> [1,100,512] 目的是为了和输入张量的维度一致
self.pe = self.pe.unsqueeze(0)
def forward(self, x):
"""
前向传播
参数:
x: 输入张量 [batch_size, seq_len, d_model]
返回:
添加位置编码后的张量
"""
seq_len = x.size(1)
# x 维度 [3, 5, 512]
# 将位置编码添加到输入张量中
print("self.pe[:, :seq_len]:", self.pe[:, :seq_len].shape) # [1, 5, 512]
x = x + self.pe[:, :seq_len]
print("x:", x.shape) # [3, 5, 512]
return self.dropout(x)
if __name__ == '__main__':
vocab_size = 2000 # 词表大小
embedding_dim = 512 # 词嵌入维度的大小
embeddings = Embeddings(vocab_size, embedding_dim)
embed_result = embeddings(torch.tensor([[1999, 2, 99, 4, 5], [66, 2, 3, 22, 5], [66, 2, 3, 4, 5]]))
print("embed_result.shape:", embed_result.shape)
print("embed_result", embed_result)
positional_encoding = PositionalEncoding(embedding_dim)
result = positional_encoding(embed_result)
print("result:", result)
print("result.shape:", result.shape)vocab_size 和 max_len关系
-
vocab_size:表示模型能够识别的不同词元(token)的数量。例如,如果使用一个包含30000个单词的词汇表,那么vocab_size=30000。 -
max_len:表示模型能够处理的单个序列的最大长度(即序列中词元的数量)。例如,如果设定max_len=512,那么每个输入序列最多可以包含512个词元。
torch.exp() 是 PyTorch 中的指数函数,计算输入张量中每个元素的自然指数(以 e 为底)。
其中 e ≈ 2.71828(自然对数的底数)
数学定义:
output = e^{input}函数定义:
torch.exp(input, *, out=None) → Tensor参数:
-
input(Tensor):输入张量 -
out(Tensor, optional):输出张量(可选)
返回值:
- 与输入张量形状相同的张量,每个元素都是输入对应元素的指数值
torch.log() 是 PyTorch 中的自然对数函数,计算输入张量中每个元素的自然对数(以 e 为底)。
其中 e ≈ 2.71828(自然对数的底数)
数学定义:
output = ln(input)函数定义:
torch.log(input, *, out=None) → Tensor参数:
-
input(Tensor):输入张量(必须为正数) -
out(Tensor, optional):输出张量(可选)
返回值:
- 与输入张量形状相同的张量,每个元素都是输入对应元素的自然对数值