数据结构——五十五、散列查找的性能分析(线性探测法)(王道408)

文章目录

前言
一.如何计算散列表的ASL
二.装填因子
- 1.概念
- 2.具体例子
二.聚集（堆积）现象
三.知识回顾与重要考点
结语

前言

本文通过实例分析散列表的性能指标。首先演示了如何构造散列表（长度为16，散列函数H(key)=key%13，采用线性探测法处理冲突），计算出查找成功的ASL为2.5，查找失败的ASL为7。当删除元素20后，查找成功的ASL变为2.63。其次介绍了装填因子α的概念，指出α接近0.7-0.8时应考虑扩大散列表。最后解释了聚集现象，说明线性探测法容易导致同义词和非同义词堆积，影响查找效率。通过具体案例（散列表长度27，H(key)=key%23）展示了聚集现象的表现形式。

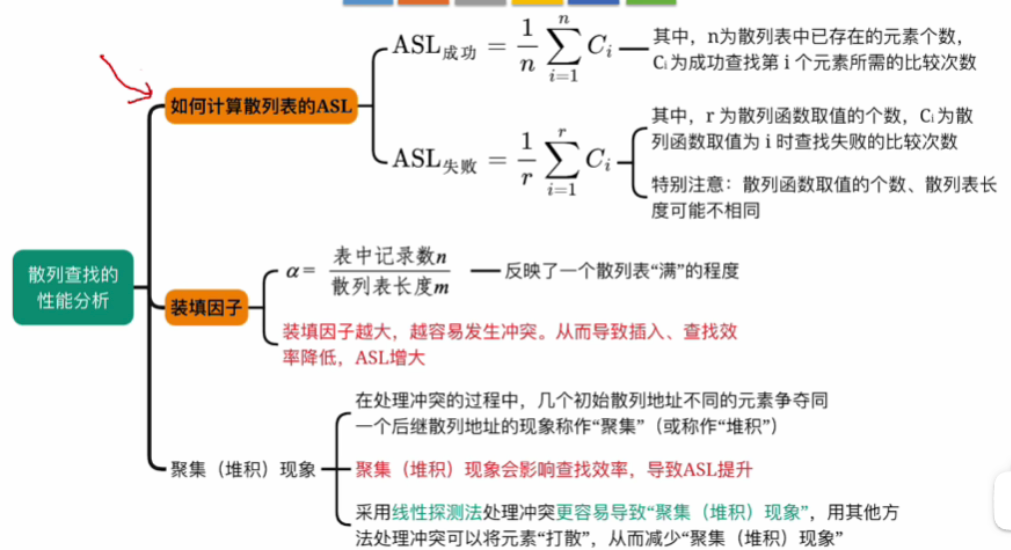
一.如何计算散列表的ASL

例：设散列表H长度为16，初始为空。散列函数H(key)=key%13，处理冲突采用线性探测法。依次插入关键字序列{19，14，23，1，68，20，84，27，55，11，10，79}

请画出所构造的散列表
1. 计算地址 H ( 19 ) = 19 % 13 = 6 H ( 14 ) = 14 % 13 = 1 H ( 23 ) = 23 % 13 = 10 H ( 1 ) = 1 % 13 = 1 → 2 H ( 68 ) = 68 % 13 = 3 H ( 20 ) = 20 % 13 = 7 H ( 84 ) = 84 % 13 = 6 → 7 → 8 H ( 27 ) = 27 % 13 = 1 → 2 → 3 → 4 → 5 H ( 55 ) = 55 % 13 = 3 → 4 → 5 H ( 11 ) = 11 % 13 = 11 H ( 79 ) = 79 % 13 = 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 \begin{aligned} &H(19)=19\%13=6\\ &H(14)=14\%13=1\\ &H(23)=23\%13=10\\ &H(1)=1\%13=1→2\\ &H(68)=68\%13=3\\ &H(20)=20\%13=7\\ &H(84) = 84\% 13 = 6\rightarrow 7\rightarrow 8\\ &H(27) = 27\% 13 = 1\rightarrow 2\rightarrow 3\rightarrow 4\rightarrow 5\\ &H(55) = 55\% 13 = 3\rightarrow 4\rightarrow 5\\ &H(11) = 11\% 13 = 11\\ &H(79) = 79\% 13 = 1\rightarrow 2\rightarrow 3\rightarrow 4\rightarrow 5\rightarrow 6\rightarrow 7\rightarrow 8\rightarrow 9 \end{aligned} H(19)=19%13=6H(14)=14%13=1H(23)=23%13=10H(1)=1%13=1→2H(68)=68%13=3H(20)=20%13=7H(84)=84%13=6→7→8H(27)=27%13=1→2→3→4→5H(55)=55%13=3→4→5H(11)=11%13=11H(79)=79%13=1→2→3→4→5→6→7→8→9
2. 插入元素
请计算在等概率情况下，查找成功、查找失败的平均查找长度ASL。
1. 由于是等概率情况下,因此任何一个元素被查找的概率都是1/12,假设现在要查找的是14,从上面地址的计算结果来看,我们可以直接通过计算14的散列地址查找到14,没有发生冲突,因此14的查找成功的查找长度为1
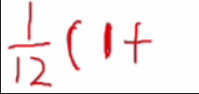
2. 接下来就是假设查找1这个元素,从上面地址的计算结果可以看出,1是经过一次冲突才能找到,因此成功查找长度为2
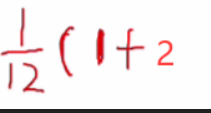
3. 其他也是类似,最终表达式如下: A S L 成功 = 1 + 1 + 1 + 2 + 1 + 1 + 3 + 4 + 3 + 1 + 3 + 9 12 = 2.5 ASL_{\text{成功}}=\frac{1+1+1+2+1+1+3+4+3+1+3+9}{12}=2.5 ASL成功=121+1+1+2+1+1+3+4+3+1+3+9=2.5
4. 观察这个散列函数H(key)=key%13,这个散列函数有可能得到的初始散列地址总共有13种,因此查找的任何一个关键字,计算出的初始散列地址只有0~12
5. 假设在查找失败的这种前提下,关键字的初始散列地址落在0~12这13个位置处的概率都是完全相等的
6. 假设此时H(key) = 0,那么由于散列表中的0这个位置为空,因此可以直接确定查找失败,那么其查找失败的长度为1
7. 假设此时H(key) = 1,由于只有在探测到空位置(或者需要探测整个表,回到起点)的前提下才能确定查找失败,因此此时的平均查找长度为13
8. 其他也是类似,所以最终表达式如下: A S L 失败 = 1 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 13 = 7 ASL_{失败}=\frac{1+13+12+11+10+9+8+7+6+5+4+3+2}{13}=7 ASL失败=131+13+12+11+10+9+8+7+6+5+4+3+2=7

A S L 失败 = 1 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 1 + 1 16 ASL_{失败}=\frac{1+13+12+11+10+9+8+7+6+5+4+3+2+1+1+1}{16} ASL失败=161+13+12+11+10+9+8+7+6+5+4+3+2+1+1+1
经典错误！注意：虽然散列表长度为16，但散列函数的取值范围仅有13种可能性

若删除元素20，请再计算在等概率情况下，查找成功、查找失败的平均查找长度ASL。
1. 注意删除20时是使用的逻辑删除而非物理删除,因此在计算查找长度的这个过程时,需要将其看做非空,这样才能继续查找下去
2. 由于删除了20,所以此时只有11个元素能被查找成功,还是根据1)中计算出的散列地址可以得出此时的平均成功查找长度: A S L 成功 = 1 + 1 + 1 + 2 + 1 + 3 + 4 + 3 + 1 + 3 + 9 11 = 2.63 ASL_{成功}=\frac{1+1+1+2+1+3+4+3+1+3+9}{11}=2.63 ASL成功=111+1+1+2+1+3+4+3+1+3+9=2.63
3. 因此此时的7只是逻辑删除,所以和之前一样: A S L 失败 = 1 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 13 = 7 ASL_{失败}=\frac{1+13+12+11+10+9+8+7+6+5+4+3+2}{13}=7 ASL失败=131+13+12+11+10+9+8+7+6+5+4+3+2=7

二.装填因子

1.概念

装填因子反映了一个散列表"满"的程度,公式如下: 散列表的装填因子 α = 表中记录数 n 散列表长度 m 散列表的装填因子 \alpha =\frac{\text{表中记录数}n}{\text{散列表长度}m} 散列表的装填因子α=散列表长度m表中记录数n
装填因子越大，越容易发生冲突。从而导致插入、查找操作效率降低，ASL增大
当α接近0.7-0.8时，应考虑扩大哈希表的大小(rehash)