9.二叉树(一) - 技术栈

一.树概念及结构

1.树的概念

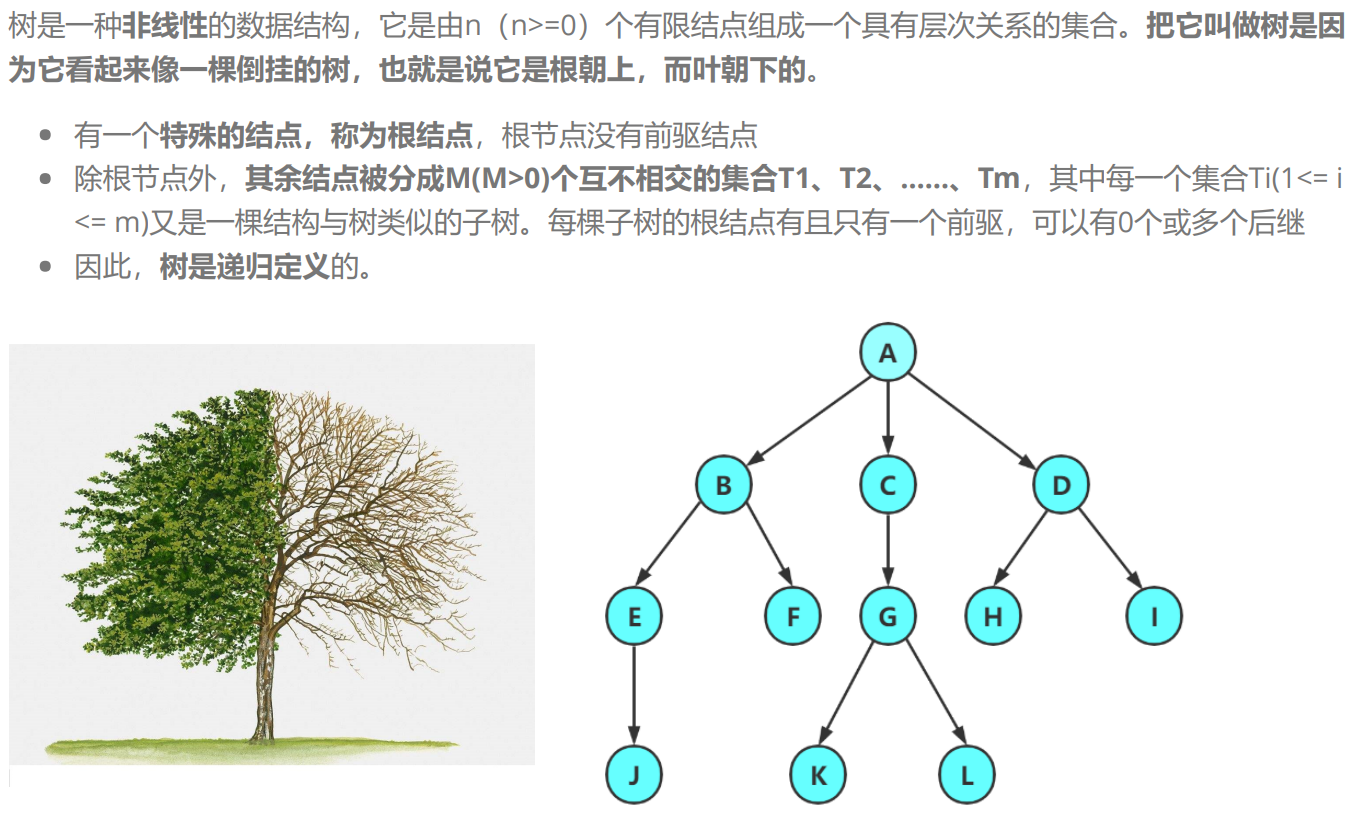
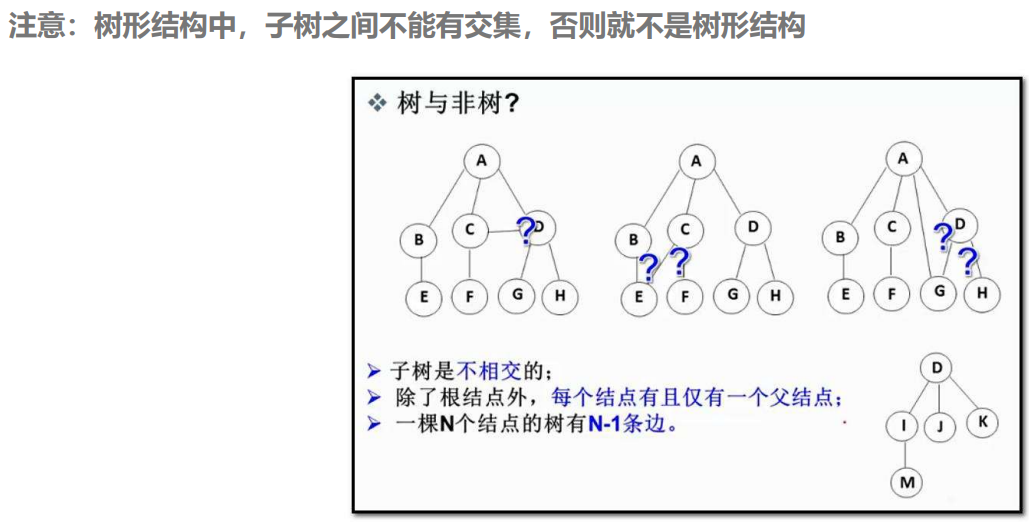
2.树的相关概念

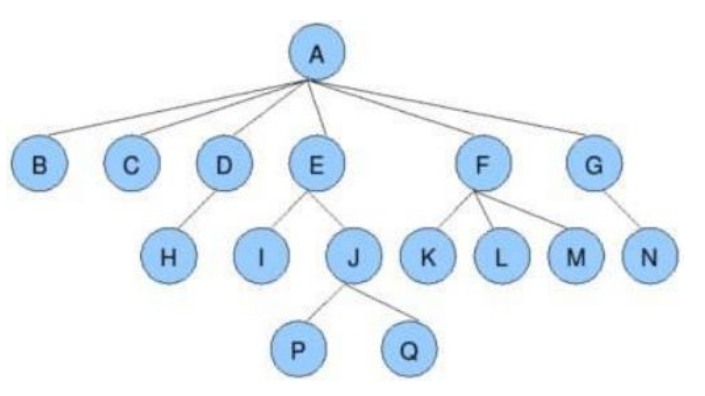
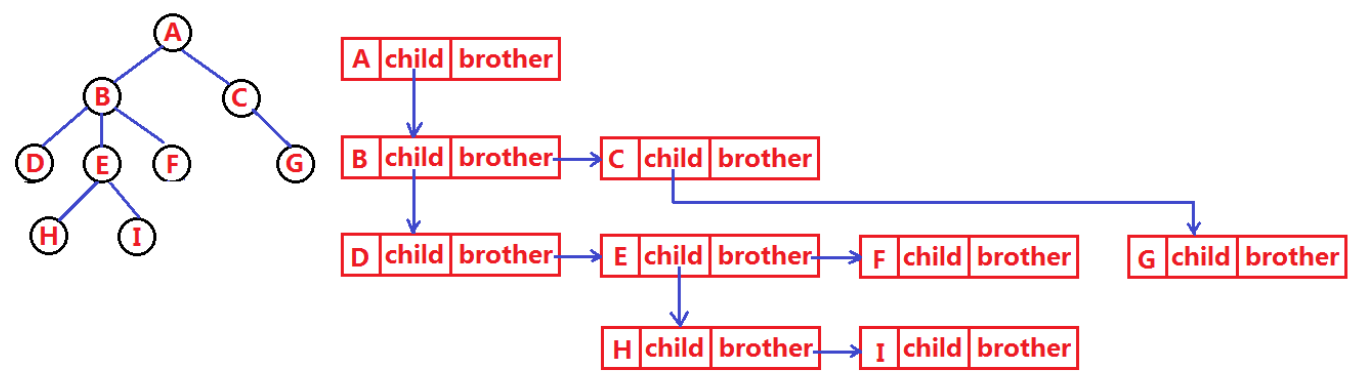
3.树的表示

cpp 复制代码

struct TreeNode
{
    int val;
    struct TreeNode* leftChild;
    struct TreeNode* nextBrother;
};

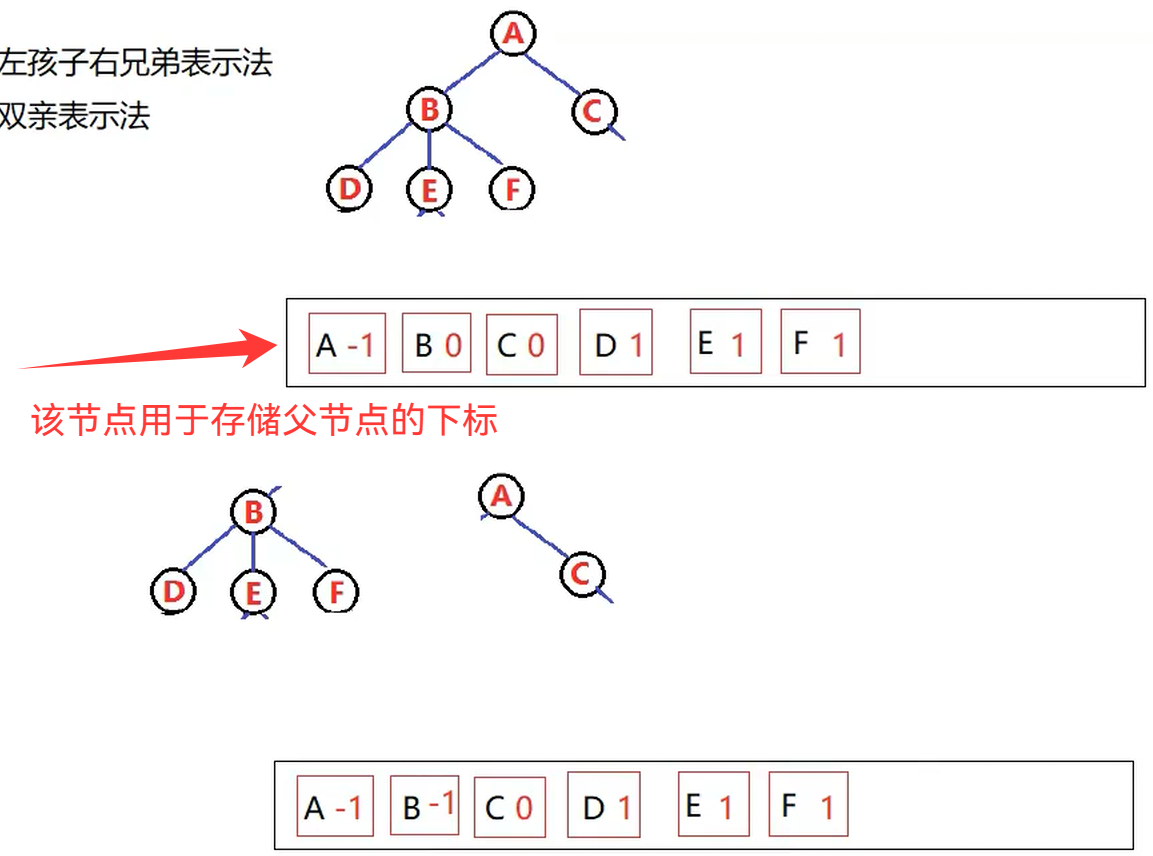
4.树在实际中的运用（表示文件系统的目录树结构）

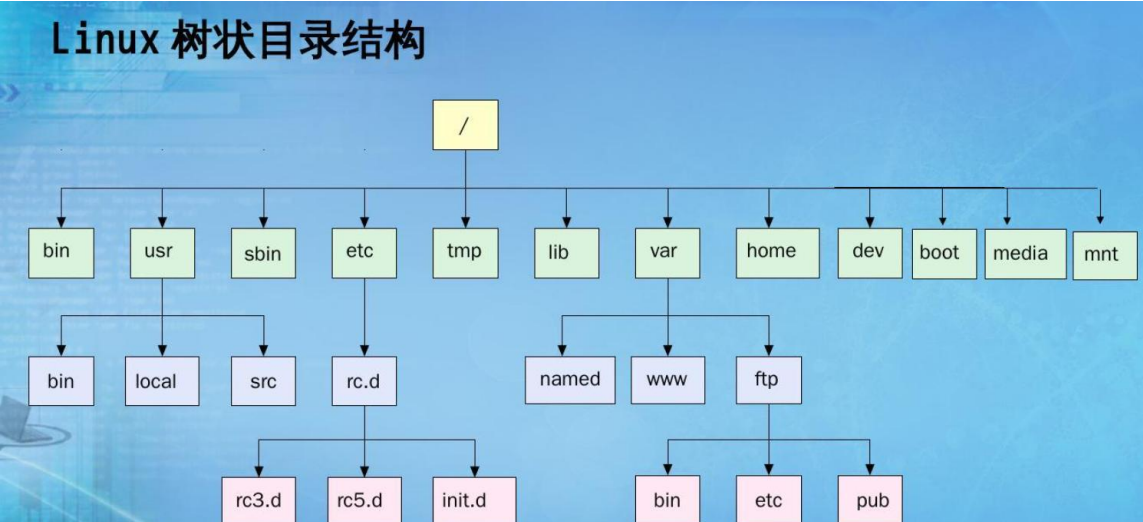
二.二叉树概念及结构

1.概念

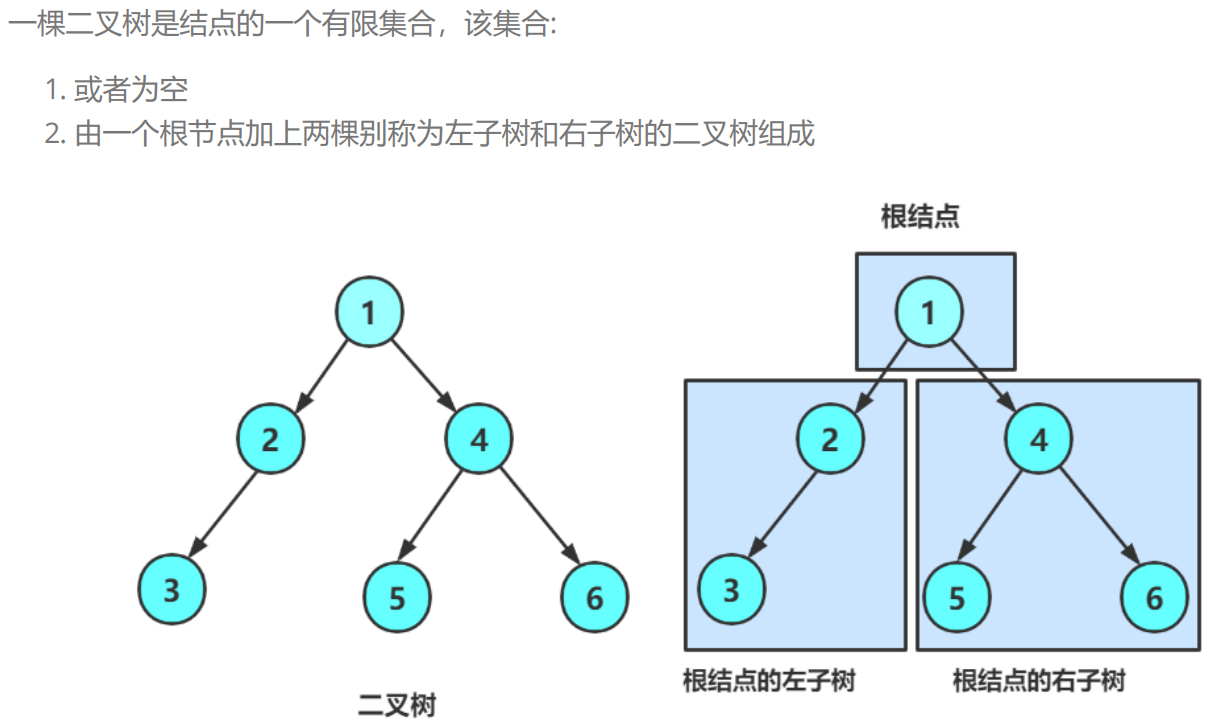
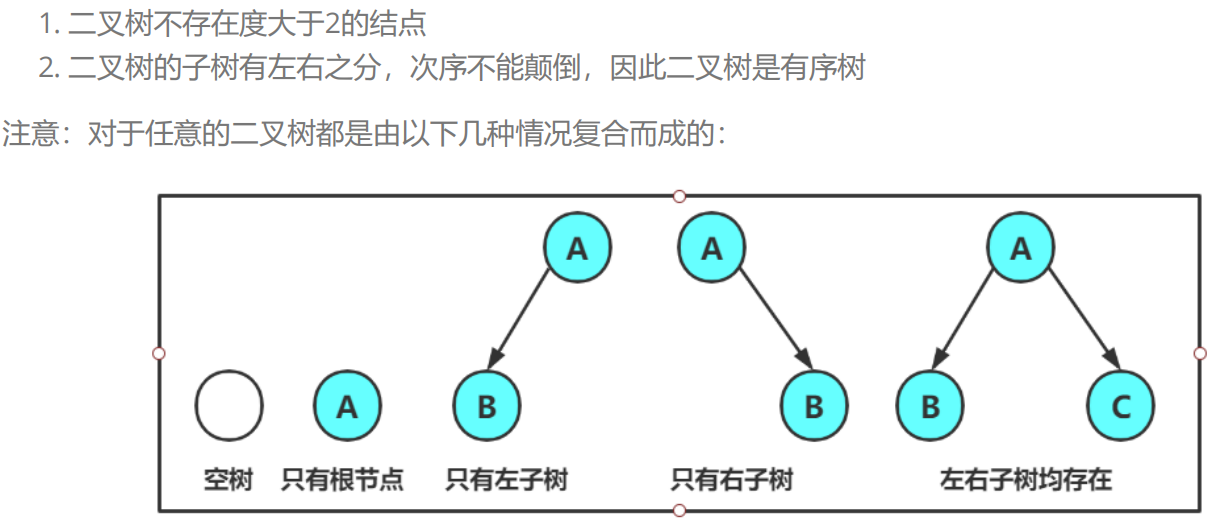
学习二叉树的意义就是,学习搜索二叉树

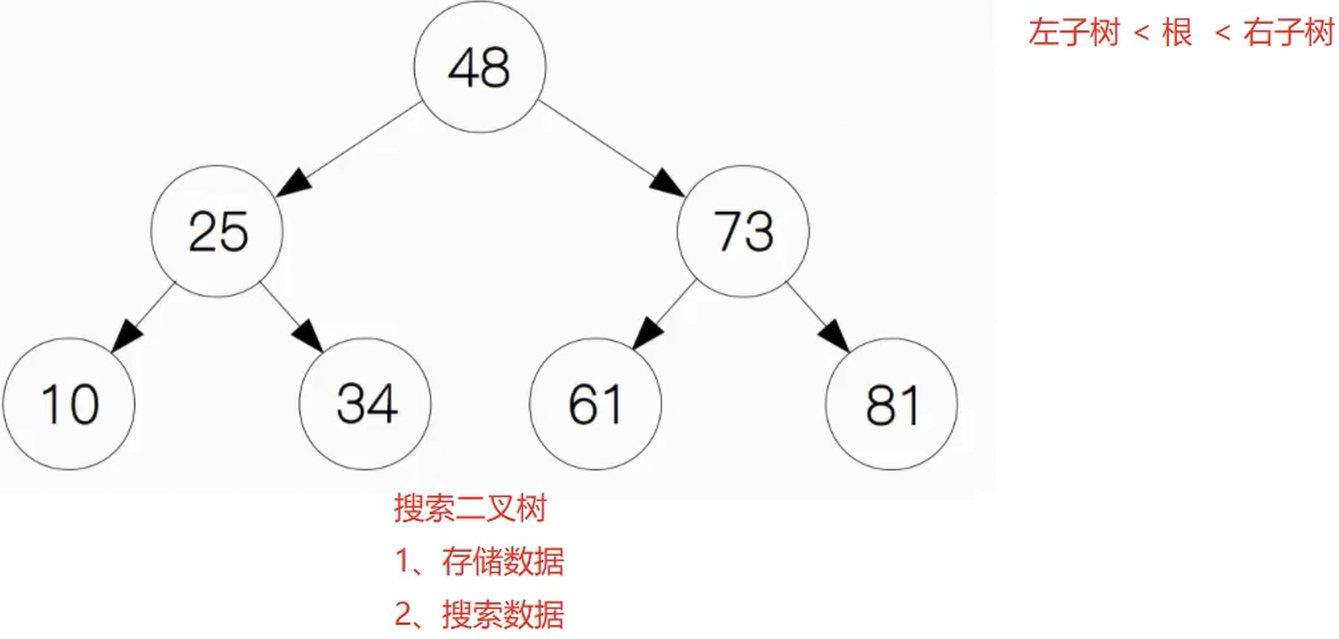
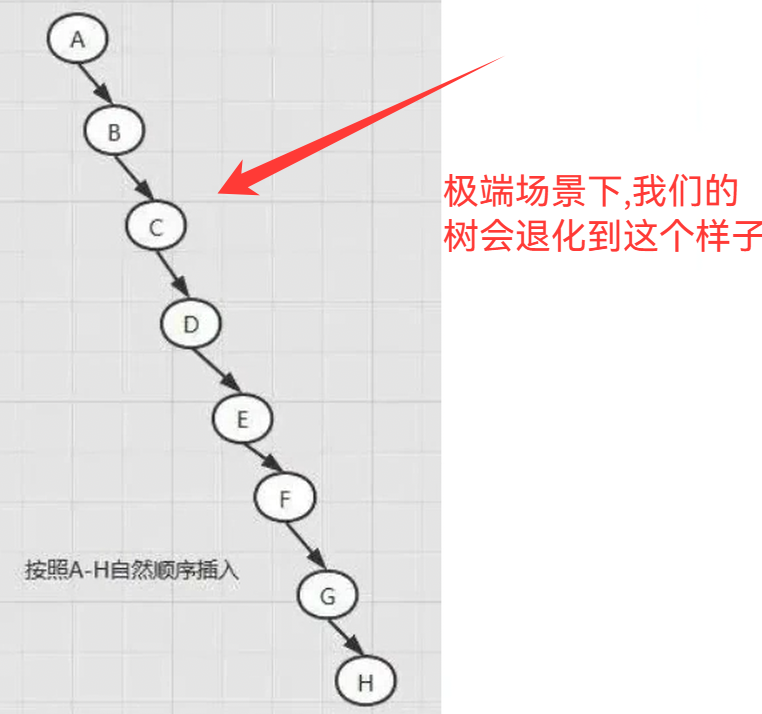
最好效率O(log n),最差效率O(n)

2.现实中的二叉树：

3.特殊的二叉树：

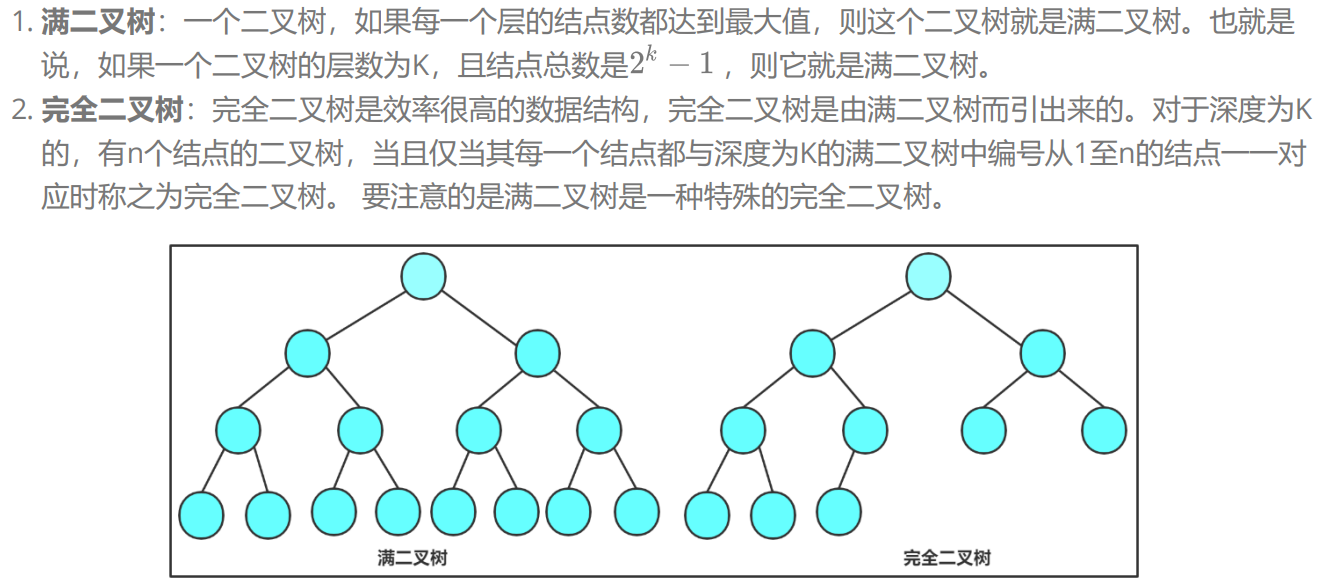
满二叉树就是完全二叉树

4.二叉树的性质

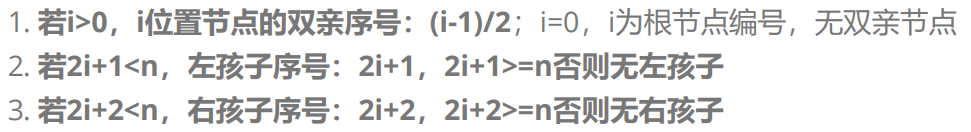
5.二叉树的存储结构

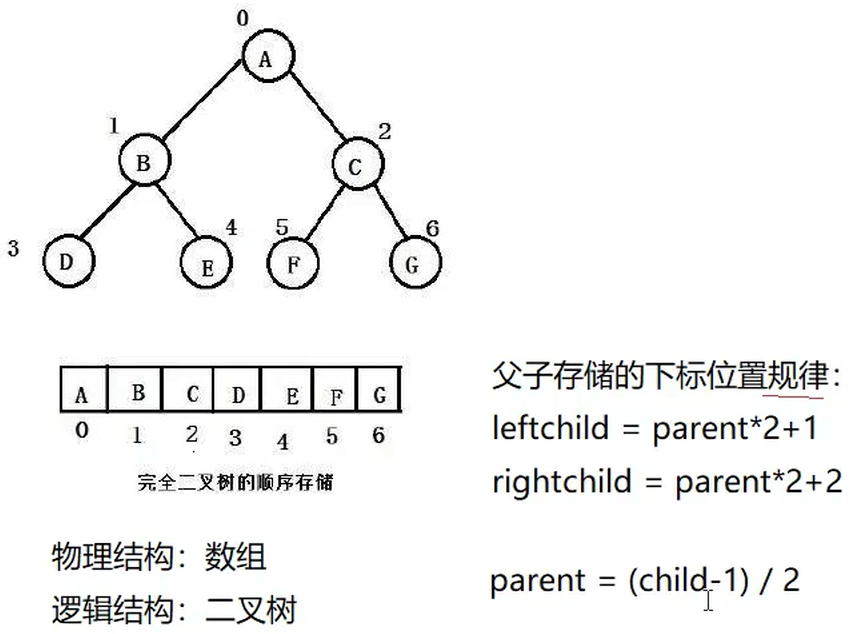
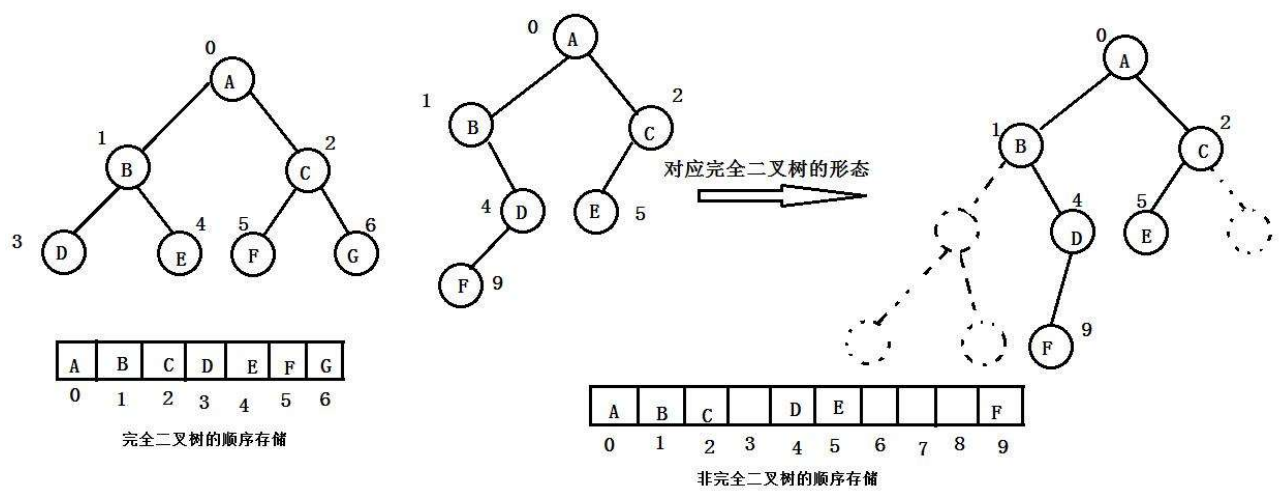
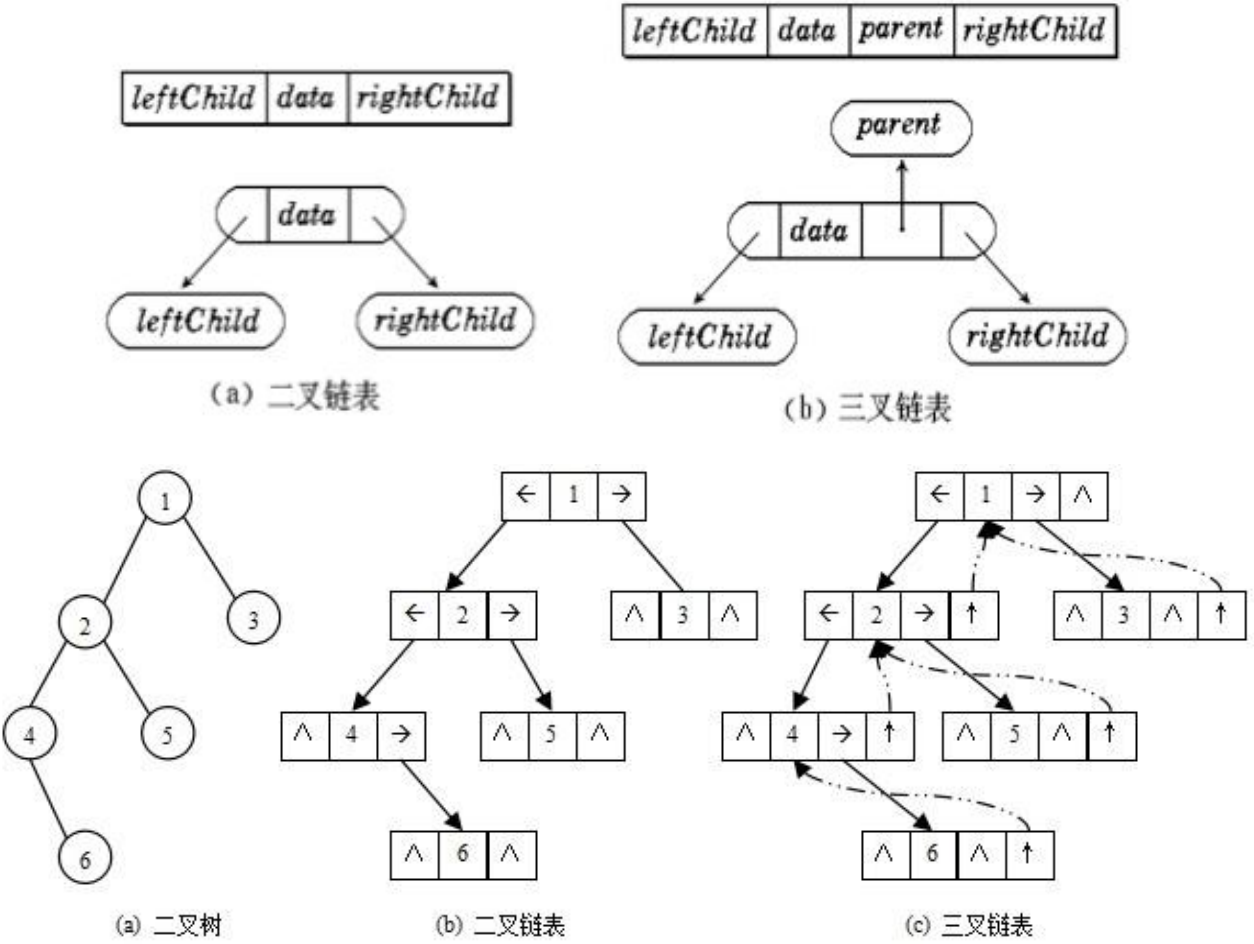
cpp 复制代码

typedef int BTDataType;

// 二叉链
struct BinaryTreeNode
{
    struct BinTreeNode* _pLeft;  // 指向当前节点左孩子
    struct BinTreeNode* _pRight; // 指向当前节点右孩子
    BTDataType _data;            // 当前节点值域
};

// 三叉链
struct BinaryTreeNode
{
    struct BinTreeNode* _pParent; // 指向当前节点的双亲
    struct BinTreeNode* _pLeft;   // 指向当前节点左孩子
    struct BinTreeNode* _pRight;  // 指向当前节点右孩子
    BTDataType _data;             // 当前节点值域
};

三.二叉树的顺序结构及实现

1.二叉树的顺序结构

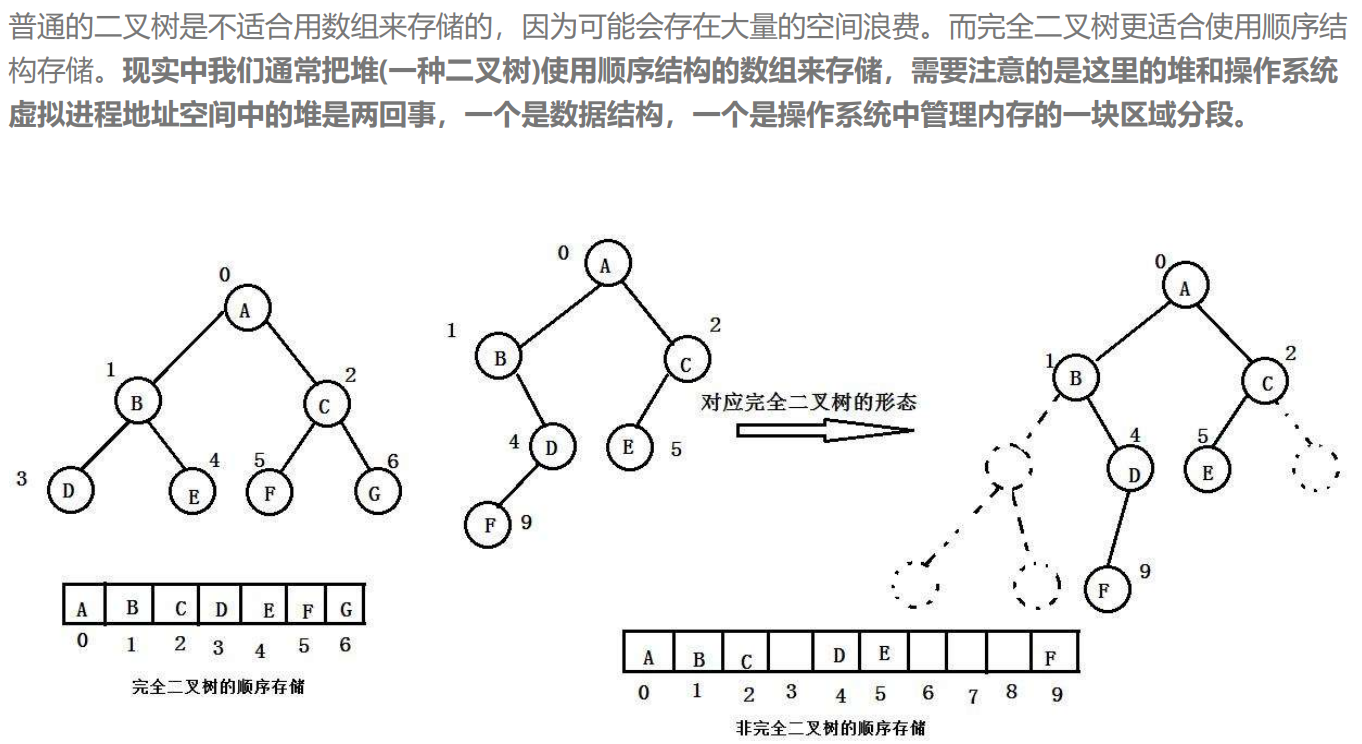
2.堆的概念及结构

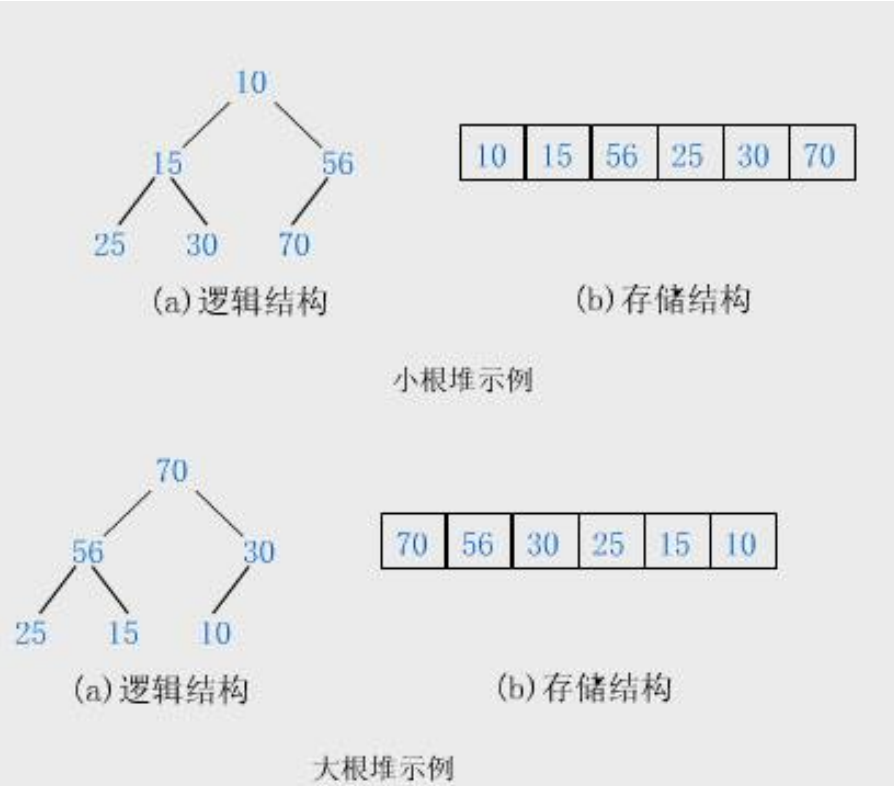
堆在数组里面是没有顺序的,兄弟之间没有关系,只有父子之间有大小关系

我们可以通过堆排序,来将其最大(或者最小)的找到

3.堆的实现

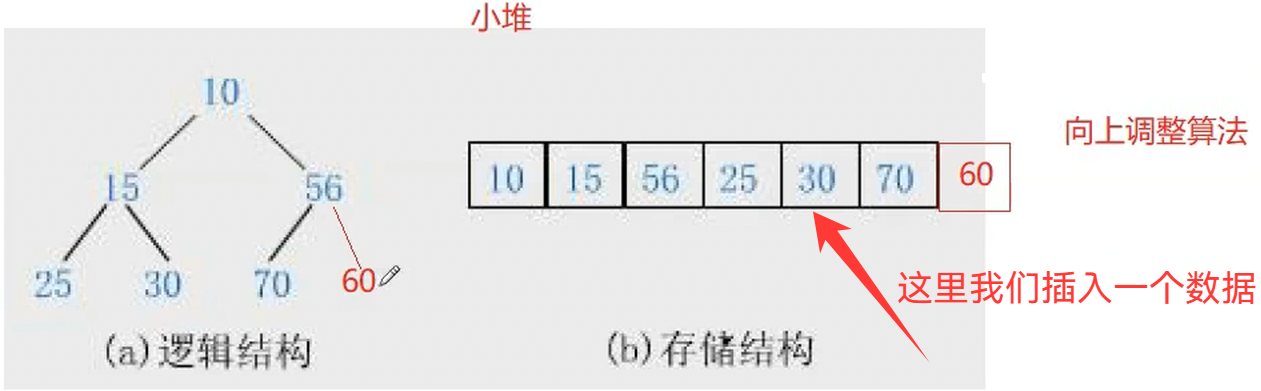
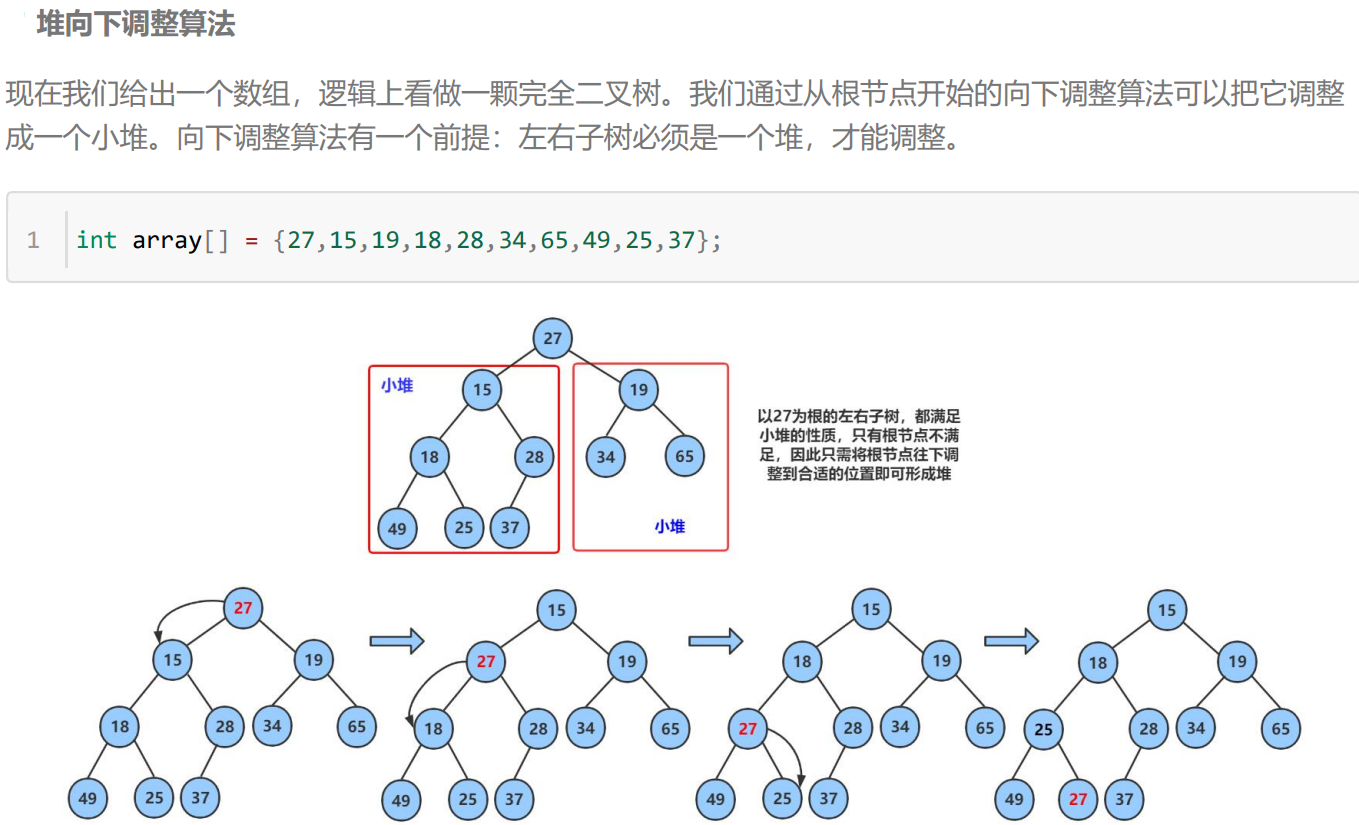
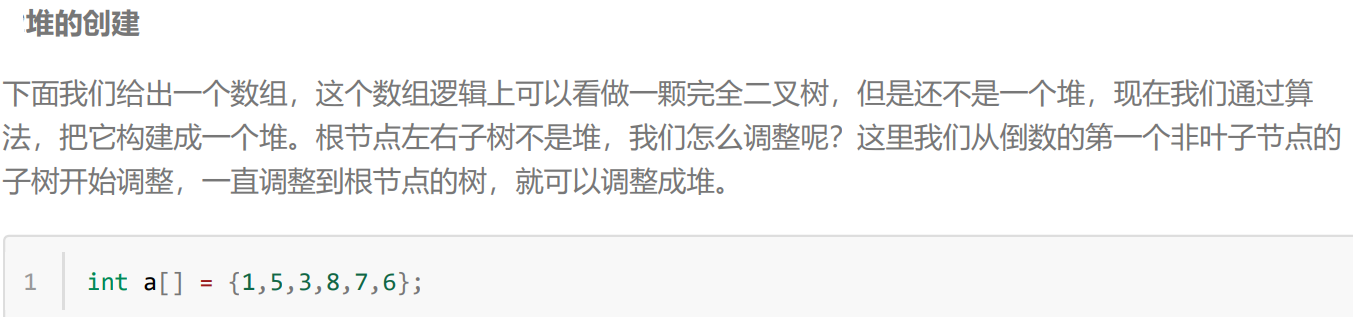
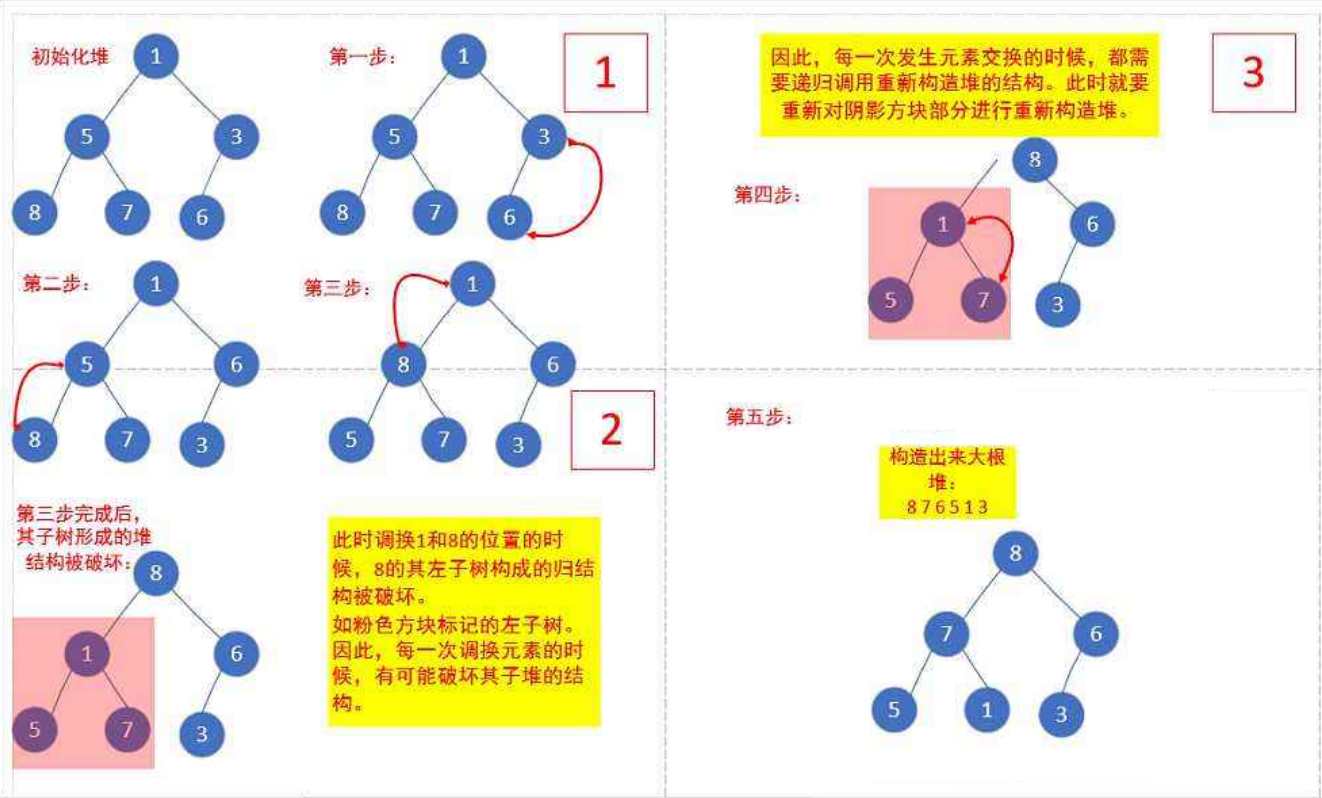
1.heap.h

cpp 复制代码

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<string.h>

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

void HPInit(HP* php);
void HPInitArray(HP* php, HPDataType* a, int n);

void HPDestroy(HP* php);
// 插入后保持数据是堆
void HPPush(HP* php, HPDataType x);
HPDataType HPTop(HP* php);

// 删除堆顶的数据
void HPPop(HP* php);

bool HPEmpty(HP* php);

void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);

2.heap.c

cpp 复制代码

#include"Heap.h"

void HPInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

void HPInitArray(HP* php, HPDataType* a, int n)
{
	assert(php);
	
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
		perror("malloc fail");
		return;
	}
	memcpy(php->a, a, sizeof(HPDataType) * n);
	php->capacity = php->size = n;

	// 向上调整，建堆 O(N*logN)
	//for (int i = 1; i < php->size; i++)
	//{
	//	AdjustUp(php->a, i);
	//}

	// 向下调整，建堆 O(N)
	for (int i = (php->size-1 - 1)/2; i >= 0; i--)
	{
		AdjustDown(php->a, php->size, i);
	}
}

void HPDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

void Swap(HPDataType* px, HPDataType* py)
{
	HPDataType tmp = *px;
	*px = *py;
	*py = tmp;
}

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	//while (parent >= 0)
	while(child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

// 时间复杂度：
void HPPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size-1);
}

HPDataType HPTop(HP* php)
{
	assert(php);

	return php->a[0];
}

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 假设法，选出左右孩子中小的那个孩子
		if (child+1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

// 时间复杂度：logN
void HPPop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}


bool HPEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}

3.test.c

cpp 复制代码

#include<stdio.h>

#include"Heap.h"

int main()
{
	//int a[] = { 50,100,70,65,60,32 };
	int a[] = { 60,70,65,50,32,100 };

	HP hp;
	HPInit(&hp);
	for (int i = 0; i < sizeof(a)/sizeof(int); i++)
	{
		HPPush(&hp, a[i]);
	}

	//printf("%d\n", HPTop(&hp));
	//HPPop(&hp);
	//printf("%d\n", HPTop(&hp));
	while (!HPEmpty(&hp))
	{
		printf("%d\n", HPTop(&hp));
		HPPop(&hp);
	}

	HPDestroy(&hp);

	return 0;
}

4.堆的分析

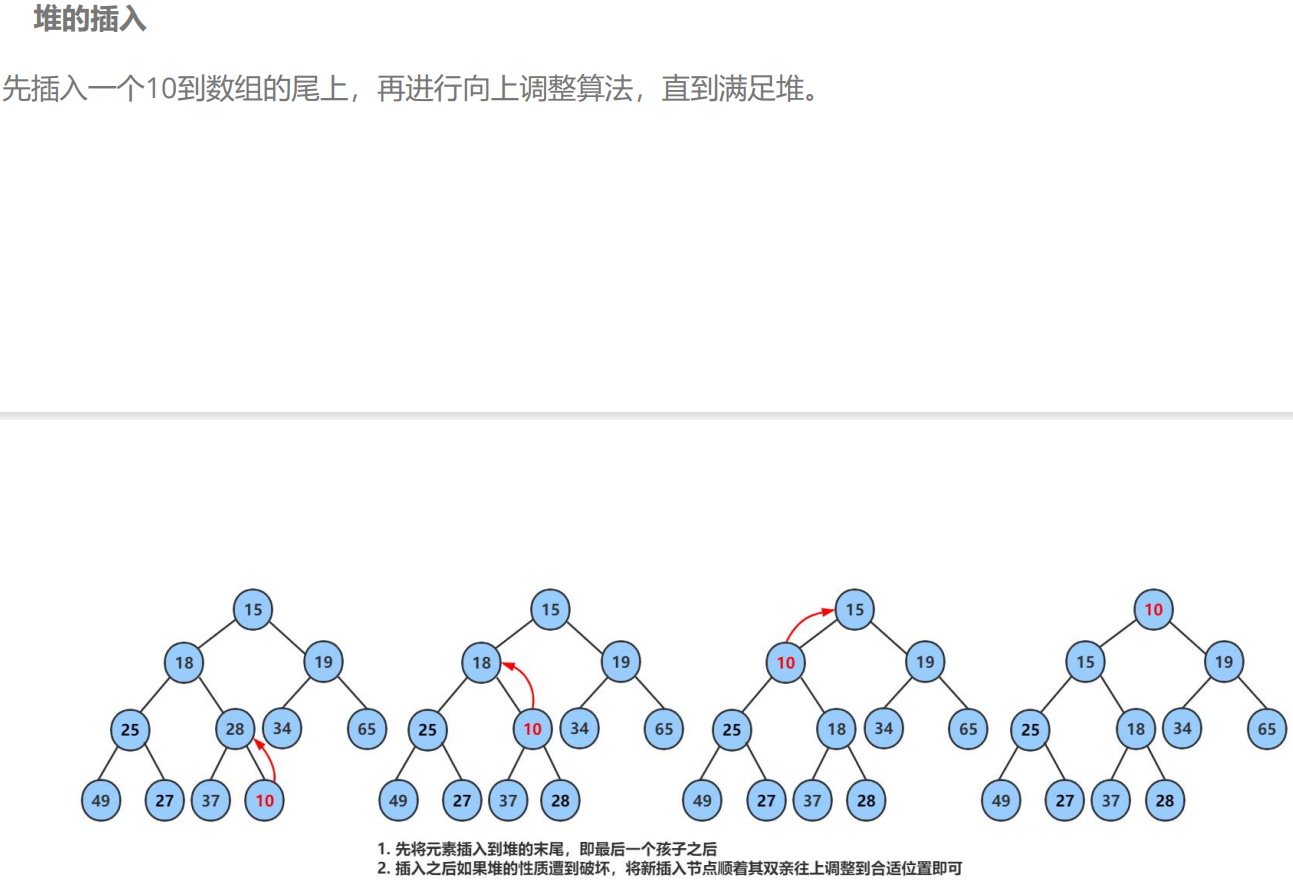
a.堆的插入

(向上调整)时间复杂度是O(log n)

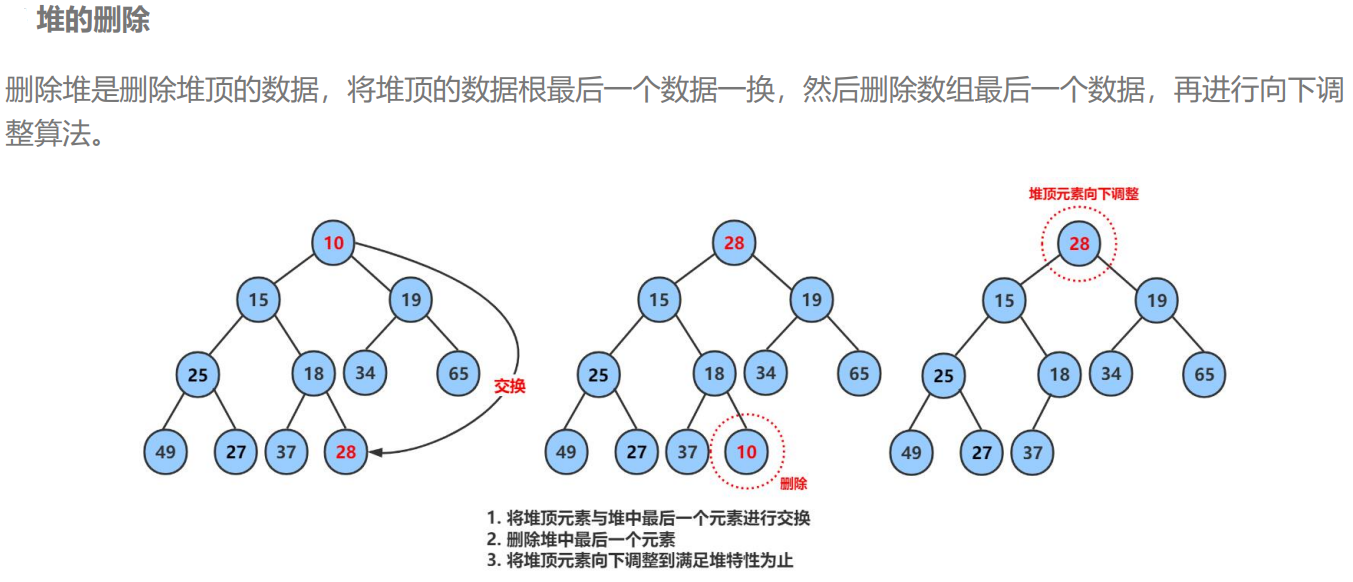
b.堆的删除

(向下调整)时间复杂度是O(log n)

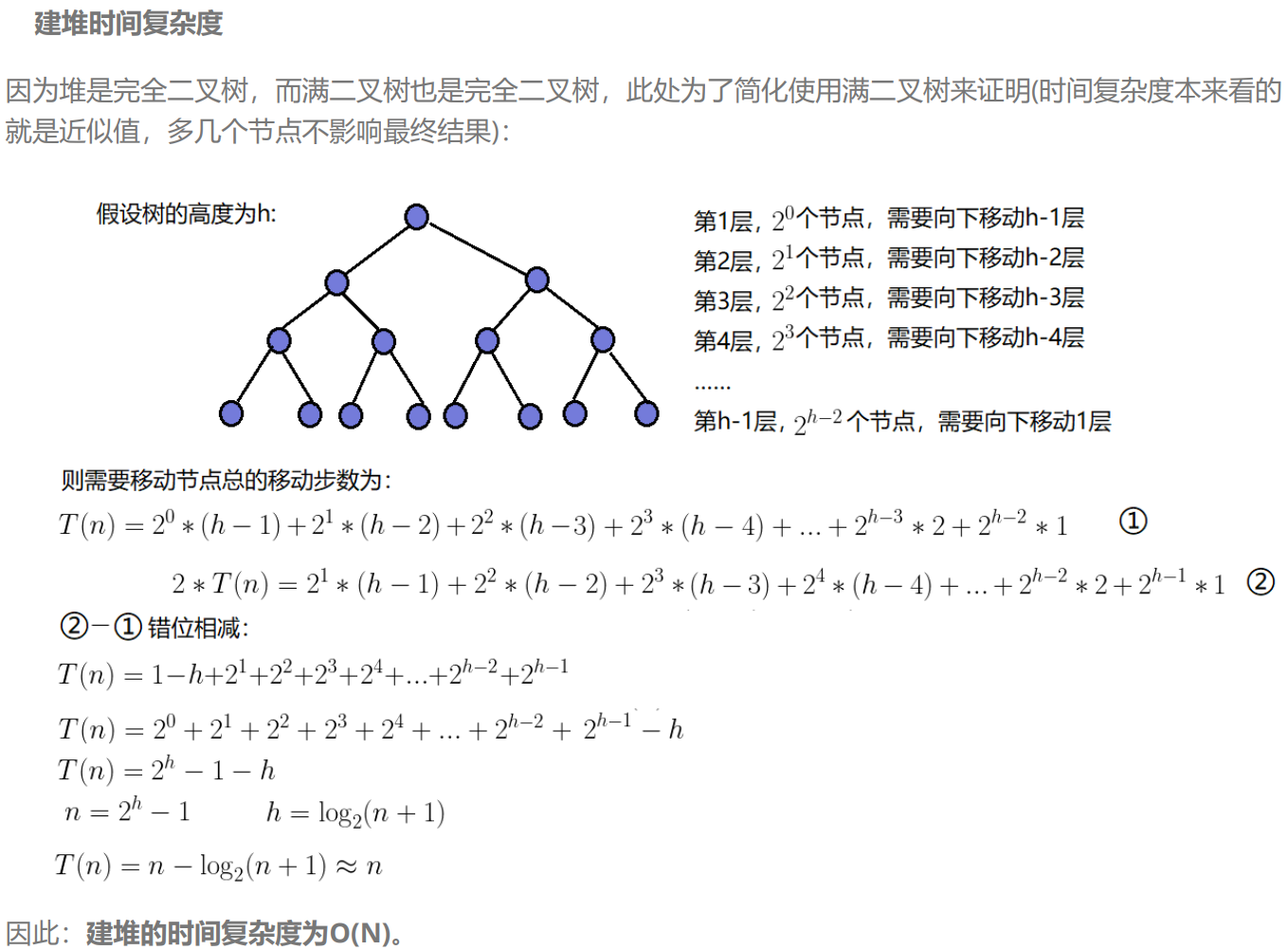
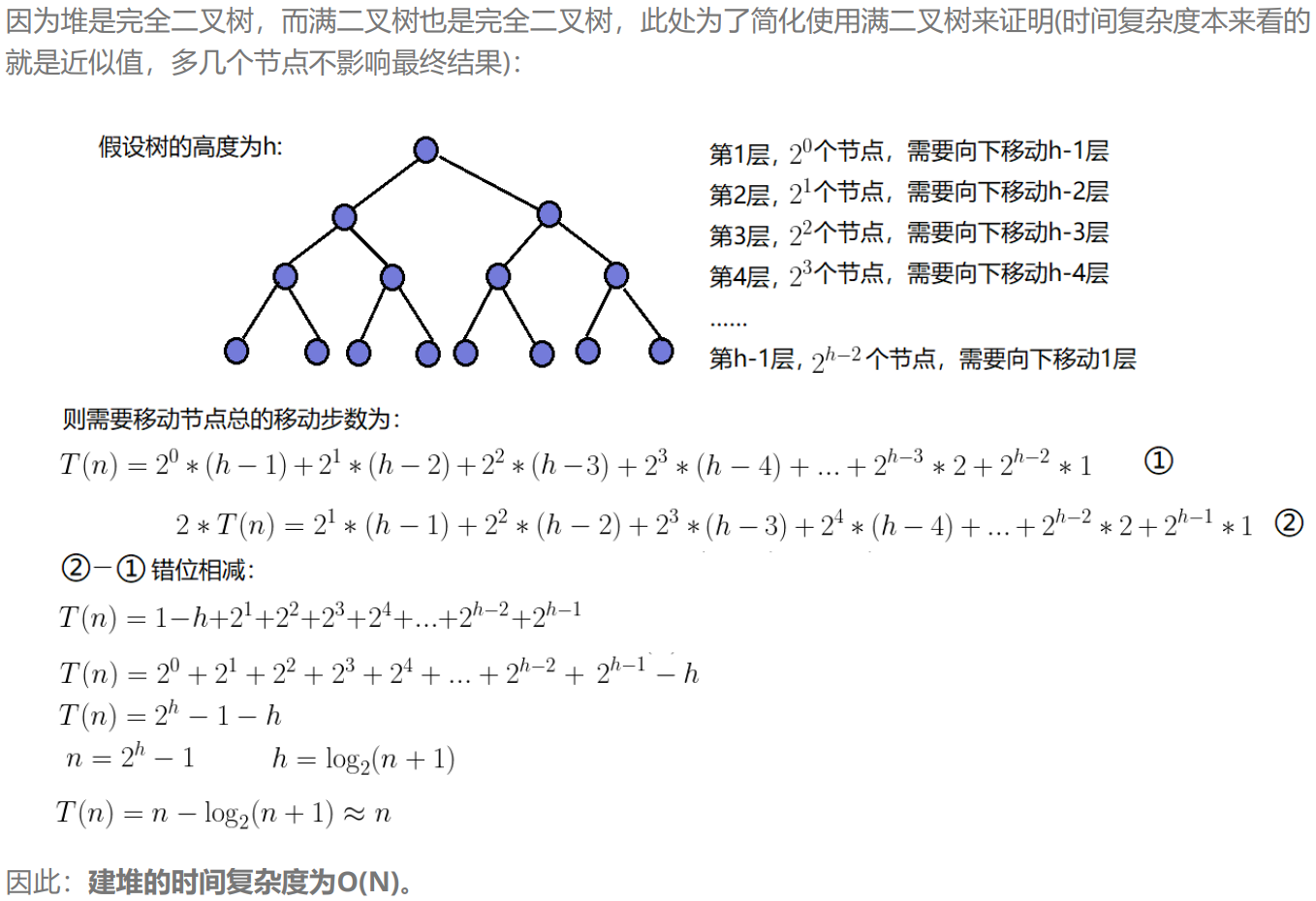
c.建堆

(向下调整建堆)时间复杂度是O(n)

(向上调整建堆)时间复杂度是O(n * log n)

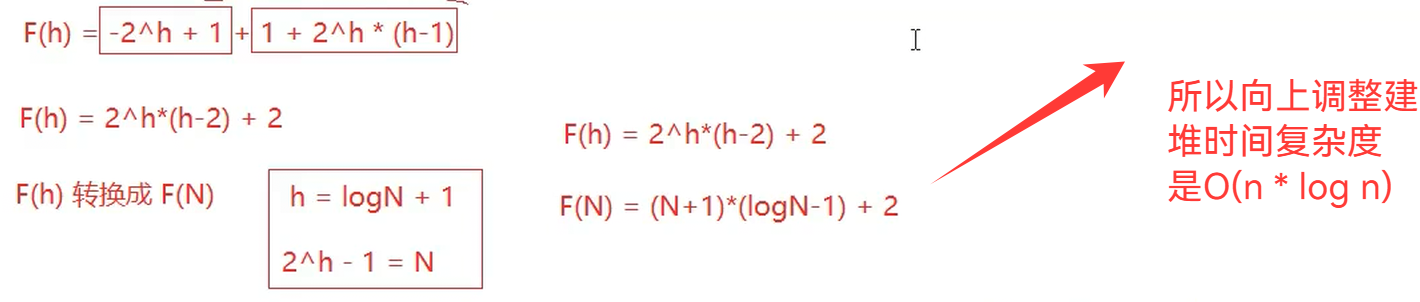
向下调整建堆,要找到第一个父亲节点(php->size - 1 - 1) / 2位置

5.堆排序

cpp 复制代码

// 1、需要堆的数据结构
// 2、空间复杂度 O(N)
void HeapSort(int* a, int n)
{
	HP hp;
	HPInitArray(&hp, a, n);

	int i = 0;
	while (!HPEmpty(&hp))
	{
		a[i++] = HPTop(&hp);

		HPPop(&hp);
	}

	HPDestroy(&hp);
}

我们可以直接使用数组进行建堆(数组可以直接进行使用)

cpp 复制代码

// 升序，建大堆还是小堆呢？大堆
// O(N*logN)
void HeapSort(int* a, int n)
{
	// a数组直接建堆 O(N)
	for (int i = (n-1-1)/2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}

	// O(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

四.堆的应用

1.堆排序

2.TOP-K问题

但是我们不能开40个G的数组啊,那怎么办呢?

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>

#include"Heap.h"


void CreateNDate()
{
	// 造数据
	int n = 100000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (int i = 0; i < n; ++i)
	{
		int x = (rand()+i) % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void topk()
{
	printf("请输入k: >");
	int k = 0;
	scanf("%d", &k);

	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}

	int val = 0;
	int* minheap = (int*)malloc(sizeof(int) * k);
	if (minheap == NULL)
	{
		perror("malloc error");
		return;
	}

	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minheap[i]);
	}

	// 建k个数据的小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(minheap, k, i);
	}

	int x = 0;
	while (fscanf(fout, "%d", &x) != EOF)
	{
		// 读取剩余数据，比堆顶的值大，就替换他进堆
		if (x > minheap[0])
		{
			minheap[0] = x;
			AdjustDown(minheap, k, 0);
		}
	}
	for (int i = 0; i < k; i++)
	{
		printf("%d ", minheap[i]);
	}
	fclose(fout);
}

int main()
{
	CreateNDate();
	topk();

	return 0;
}