
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 一维前缀和](#1. 一维前缀和)
[2. 最大字段和](#2. 最大字段和)
[3. 二维前缀和](#3. 二维前缀和)
[4. 激光炸弹](#4. 激光炸弹)
前言
前缀和的核心思想是预处理,可以在暴力枚举的过程中快速查询到结果,相当于是对枚举的优化,是经典的用空间换时间的做法
1. 一维前缀和
题目链接:
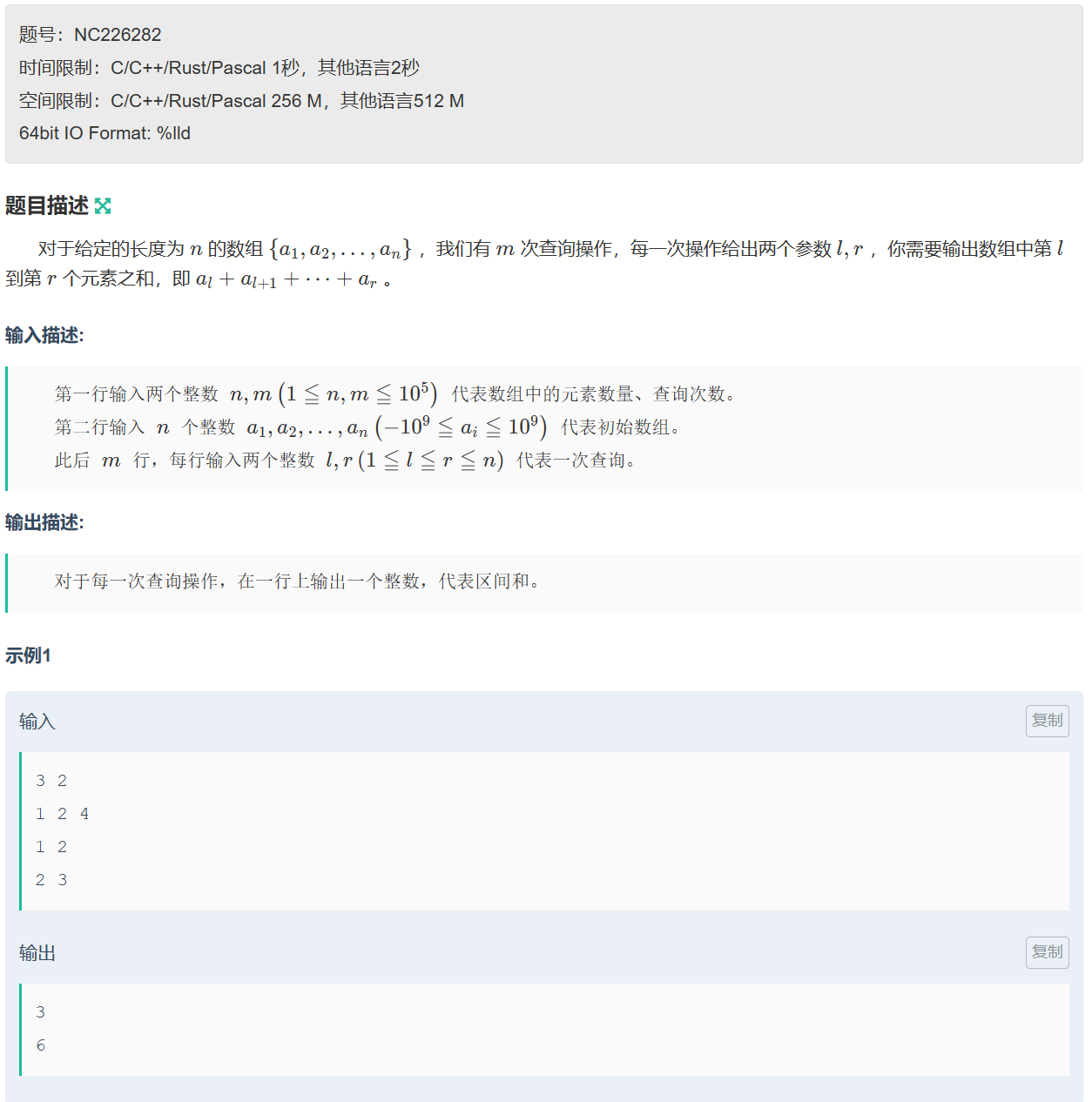
算法原理
暴力求解:
很简单,我们每次询问直接无脑从l遍历到r不就得了,不就是O(n*m),差不多10^10次方吗(
(pass)
前缀和:
由于是一个连续区间的和,注意是连续区间,我们可以这样思考
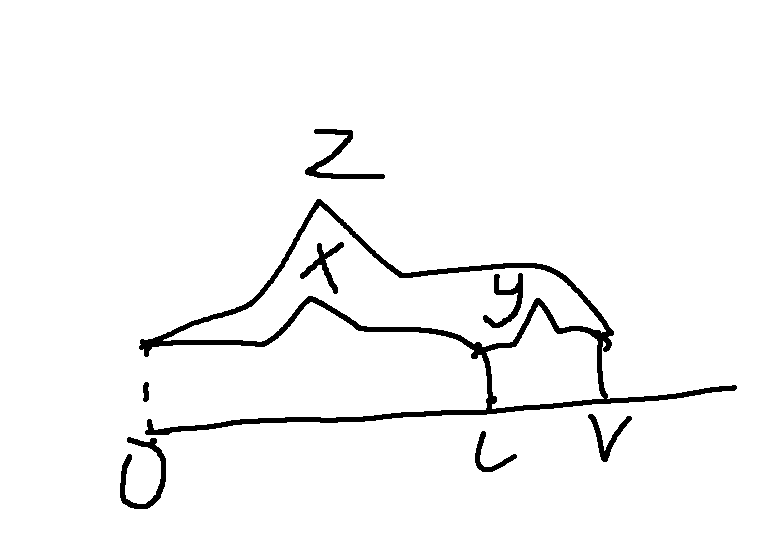
区间y的和是不是区间z的和 - 区间x的和?并且区间z和区间x的和都是从原点开始的
因此,我么可以定义一个数组f,定义f[i]为下标从0到i的数字的和,这就是前缀和数组,我们可以在一开始读取数据的时候就能初始化出来,即f[i] = f[i-1] + num
那么区间y的和不就是f[z] - f[x - 1]的值吗
至于为什么是f[x - 1]而不是f[x],因为题目给出的是闭区间,即[x,y],那么f[x]就包含v[x]这个数字,如果减f[x]就减去了v[x]
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n,m;cin>>n>>m;
vector<long long> f(n+1,0);
for(int i = 1;i<=n;i++)
{
long long num;cin>>num;
f[i] = f[i-1] +num;//预处理前缀和数组
}
while(m--)
{
int a,b;cin>>a>>b;
cout<<f[b] - f[a-1]<<endl;
}
return 0;
}2. 最大字段和
题目链接:
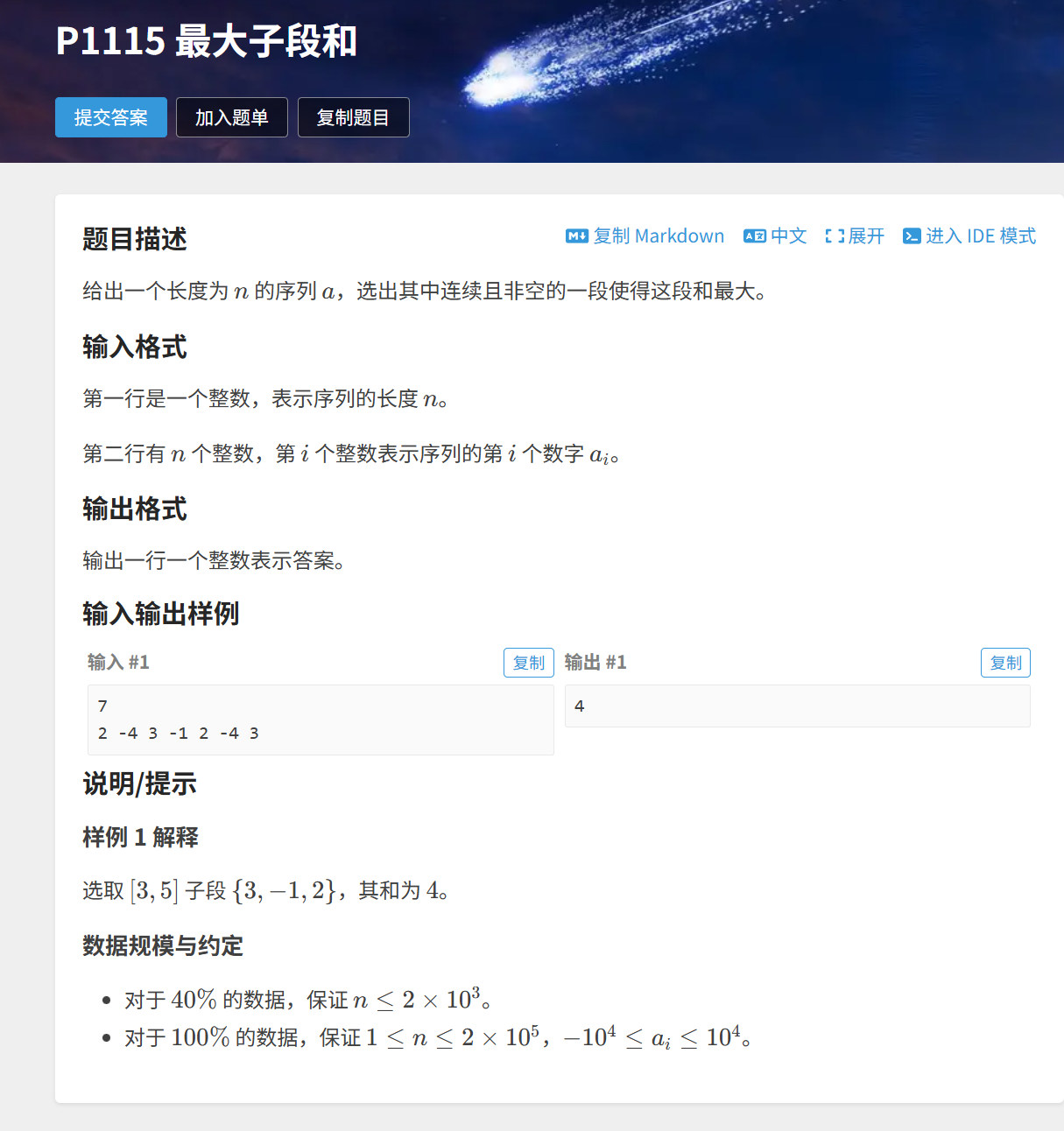
算法原理
跟上题很相似的是,同样是一个字段,即中间的一个区间的和,那么也可以用前缀和解决
由于我们要计算最大的区间的和,我们可以这样思考,区间和无非就是f[y] - f[x]的和的最大值
我们对于前缀和数组从头开始枚举,这样f[y]就确定了,那么只需要找出最小的f[x]即可
并且x 一定是小于y的
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;cin >> n;
vector<long long> f(n+1);
for(int i = 1; i <= n; i++)
{
long long x; cin >> x;
f[i] = f[i - 1] + x;
}
long long ret = -1e20;
long long prevmin = 0;//最小的前缀和区间
for(int i = 1; i <= n; i++)
{
ret = max(ret, f[i] - prevmin);
prevmin = min(prevmin, f[i]);//更新最小的前缀和区间
}
cout << ret << endl;
return 0;
}3. 二维前缀和
题目链接:
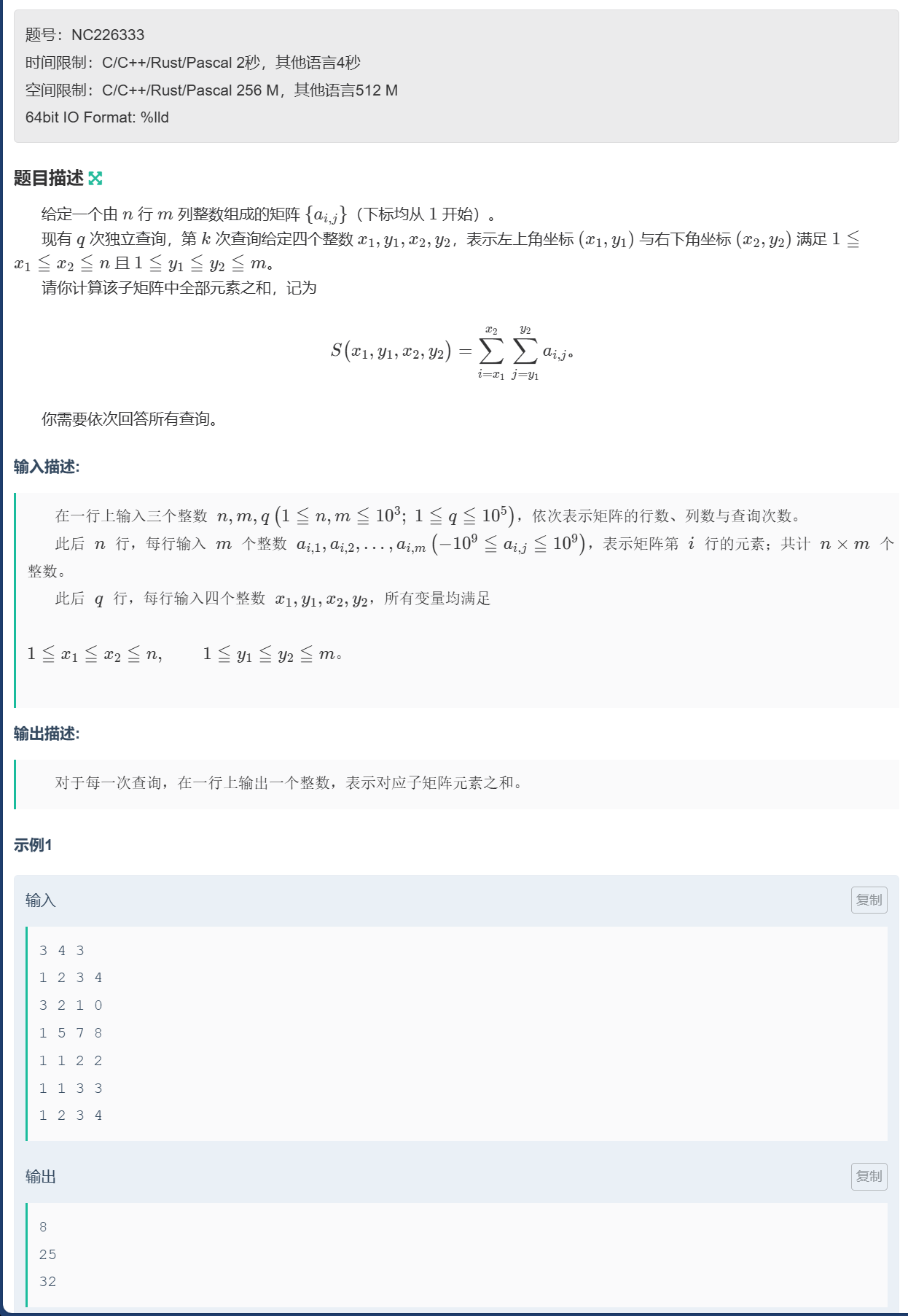
算法原理
一维前缀和f[n]是前n个数字的和,那么我们推广到二位前缀和数组可以这样定义
f[x][y]表示的是前x行,前y列的所有数的和
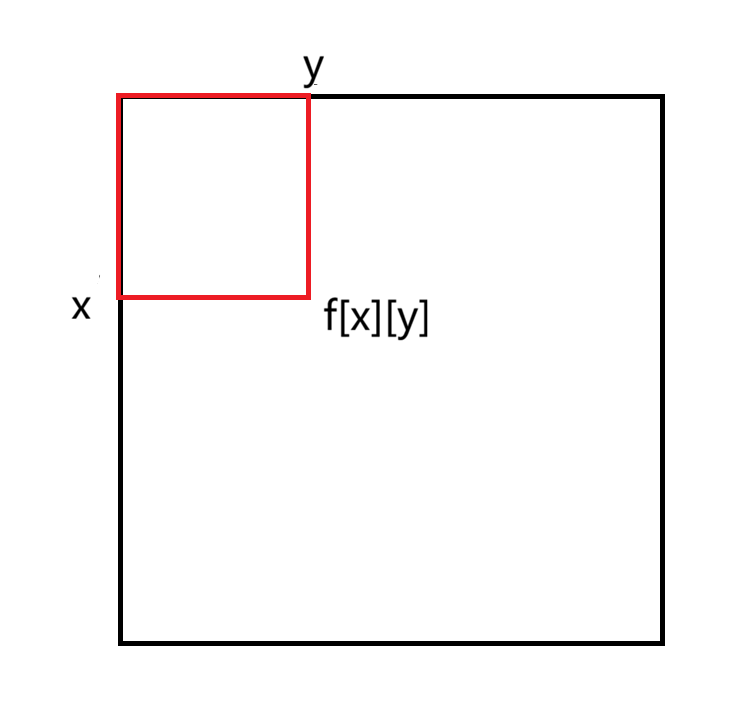
那么我们如何推导f[x][y]?
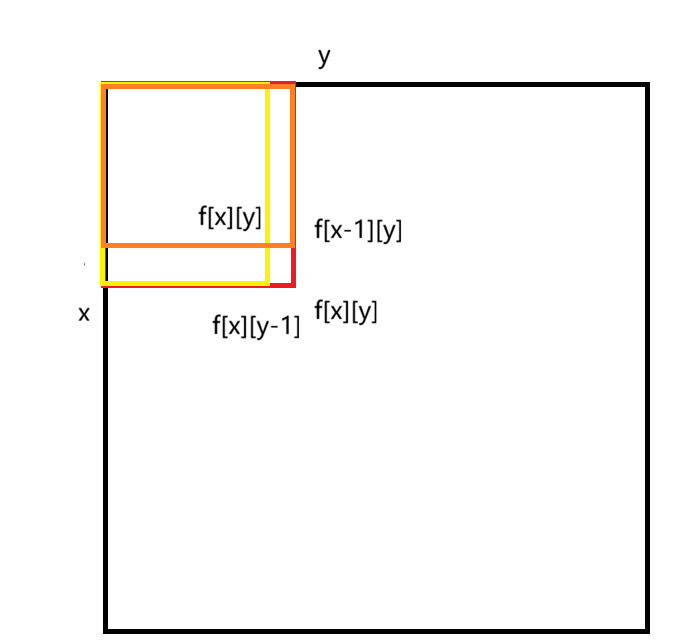
我们会发现f[x][y]要用到f[x][y-1]和f[x-1][y]中的值,同时f[x][y-1]和f[x-1][y]重合了f[x][y]
因此f[x][y] = f[x][y-1] + f[x-1][y] - f[x-1][y-1] + v[x][y]
处理了f[x][y]的值,那么如何计算(a,b)到(c,d)这之间的值?
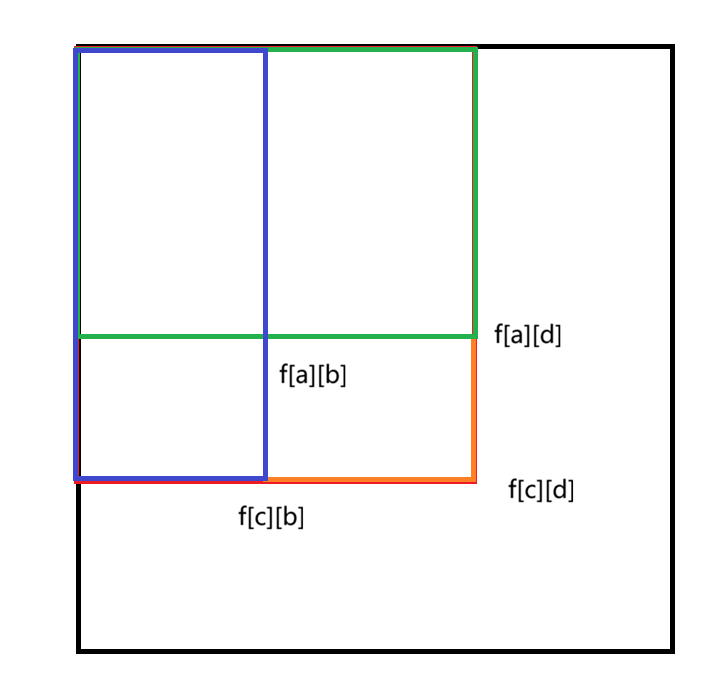
同样的道理
ret = f[c][d] - f[c][b] - f[a][d] + f[a][b]
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int a,b,c;cin>>a>>b>>c;
vector<vector<long long>> f(a+1,vector<long long>(b+1,0));
for(int i = 1;i<=a;i++)
{
for(int j = 1;j<=b;j++)
{
int num;cin>>num;
f[i][j] = f[i][j-1] + f[i-1][j] + num - f[i-1][j-1];
}
}
while(c--)
{
int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;
cout<<f[x2][y2] - f[x1-1][y2] - f[x2][y1-1] + f[x1-1][y1-1]<<endl;
}
return 0;
}4. 激光炸弹
算法原理
由于获得的价值是一个m为边长的正方形,我们假设往(x,y)这个位置扔炸弹,那么这不就是(x- m,y - m)到(x,y)的和吗?因此我们使用二位前缀和数组,以m * m的方格一行一列地枚举即可
当然如果m非常大,比整个数组的行列还要大,那么就越界访问了,因此我们得处理这种情况
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
const int MAX = 5005;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> v(MAX, vector<int>(MAX, 0));
for (int i = 0; i < n; i++) {
int x, y, value;
cin >> x >> y >> value;
v[x + 1][y + 1] += value;
}
for (int i = 1; i < MAX; i++) {
for (int j = 1; j < MAX; j++) {
v[i][j] = v[i][j] + v[i - 1][j] + v[i][j - 1] - v[i - 1][j - 1];//二维前缀和
}
}
int ret = 0;
int r = min(m, MAX - 1);//处理m>MAX的情况
for (int i = r; i < MAX; i++) {
for (int j = r; j < MAX; j++) {
int sum = v[i][j] - v[i - r][j] - v[i][j - r] + v[i - r][j - r];
if (sum > ret) {
ret = sum;
}
}
}
cout << ret;
return 0;
}