【微实验】直方图均衡化：让光影重获新生的魔法，在明暗之间编织细节的诗篇

[🌅 序章：老照片里的光影叹息](#🌅 序章：老照片里的光影叹息)

[🧐 困境：当光影被 "囚禁" 在角落](#🧐 困境：当光影被 “囚禁” 在角落)

[生活里的 "灰度困境"](#生活里的 “灰度困境”)

[技术里的 "直方图" 密码](#技术里的 “直方图” 密码)

[✨ 破局：灰度的 "迁徙计划"](#✨ 破局：灰度的 “迁徙计划”)

[核心思路：从 "占比" 到 "新地址"](#核心思路：从 “占比” 到 “新地址”)

数学支撑：从概率到映射

[🎨 进阶：不止 "平均"，更要 "自定义"](#🎨 进阶：不止 “平均”，更要 “自定义”)

[💻 实践：亲手编写直方图均衡化（MATLAB 实现）](#💻 实践：亲手编写直方图均衡化（MATLAB 实现）)

运行说明

[🌈 终章：光影的哲学](#🌈 终章：光影的哲学)

🌅 序章：老照片里的光影叹息

阁楼深处的旧相册里，总有几张照片让人怅然 ------ 要么是逆光下人脸成了剪影，阳光却白得刺眼；要么是阴雨天拍的风景，灰蒙蒙一片分不清树叶的纹理。就像记忆会模糊细节，光与影的失衡也会吞噬图像的故事。

"技术是修复时光的手，让被掩埋的细节重新呼吸。" 直方图均衡化，正是这样一种技术：它不改变画面的内容，却能重新分配光影的权重，让暗部走出阴霾，让亮部收敛锋芒，让每一寸灰度都承载起应有的故事。

🧐 困境：当光影被 "囚禁" 在角落

生活里的 "灰度困境"

你是否有过这样的经历？傍晚在室内拍文档，闪光灯一亮，纸页中央白得晃眼，边缘却暗得看不清字迹。这背后，是 "灰度范围" 的失衡 ------ 相机能捕捉的亮度层次是有限的（比如 8 位图像只有 0-255 共 256 级灰度），当场景的明暗反差过大，大部分灰度会被 "挤压" 到极暗或极亮的角落，中间的细节被彻底淹没。

就像一场音乐会，如果所有乐器都只在低音区轰鸣，或只在高音区尖叫，旋律的丰富性便无从谈起。图像的灰度分布，也需要 "高低音" 的平衡。

技术里的 "直方图" 密码

我们用 "直方图" 来描述这种分布：横轴是灰度值（0 为黑，255 为白），纵轴是该灰度对应的像素数量。

正常图像的直方图：灰度分布均匀，像平缓起伏的丘陵；
过暗图像的直方图：像素集中在左侧（低灰度区），像拥挤的山谷；
过亮图像的直方图：像素集中在右侧（高灰度区），像陡峭的悬崖；
低对比度图像的直方图：所有像素挤在中间狭窄区域，像被压缩的峡谷。

直方图均衡化的任务，就是把这些 "拥挤的灰度" 重新疏散，让它们均匀分布在 0-255 的全范围内，就像把堵塞的河流疏导成宽广的湖面，让每一滴水（像素）都有自己的位置。

✨ 破局：灰度的 "迁徙计划"

核心思路：从 "占比" 到 "新地址"

想象一群人挤在房间的角落，均衡化就像给每个人重新分配座位：先统计每个灰度值的像素占比（比如灰度 100 的像素占总像素的 5%），再按占比累计出 "累计分布函数（CDF）"，最后用 CDF 乘以最大灰度值（255），得到每个灰度的 "新地址"。

举个例子：

原图像中，灰度 0-50 的像素占比 30%，51-100 占比 20%，101-255 占比 50%；
累计后：灰度≤50 占 30%，≤100 占 50%，≤255 占 100%；
新灰度 = 累计占比 ×255：原灰度 50→30%×255≈76，原灰度 100→50%×255≈128，以此类推。

这样一来，原本拥挤的低灰度区被 "拉伸" 到更宽的范围，细节自然显现。

数学支撑：从概率到映射

设原图像灰度为r（0≤r≤255），其概率密度函数为\(p_r(r)\)（某灰度出现的概率），均衡化后的新灰度s满足：\(s = T(r) = 255 \times \int_{0}^{r} p_r(w)dw\)这个积分就是累计分布函数（CDF），它的意义是："所有小于等于 r 的灰度，总共占多少比例"。

当灰度分布均匀时，\(p_r(r)=1/256\)，CDF 是一条直线，\(s=r\)，无需调整；
当灰度集中在低区间，CDF 增长快，低灰度会被映射到更高的新灰度（暗部变亮）；
当灰度集中在高区间，CDF 增长慢，高灰度会被映射到更低的新灰度（亮部变暗）。

🎨 进阶：不止 "平均"，更要 "自定义"

标准直方图均衡化追求 "绝对均匀"，但有时我们需要更灵活的调整 ------ 比如保留夜景的暗调氛围，同时提亮星星的细节；或者增强人像的肤色层次，避免背景过度刺眼。这就需要 "自定义灰度曲线映射"：不再严格按 CDF 分配，而是根据需求设计映射关系。

常见的自定义曲线：

对数曲线：增强暗部细节（像给暗处开一盏柔和的灯）；
指数曲线：增强亮部细节（像给亮处拉一层纱）；
S 型曲线：同时提升明暗对比（像给画面加一层立体感滤镜）。

💻 实践：亲手编写直方图均衡化（MATLAB 实现）

以下代码将实现 "标准直方图均衡化" 和 "3 种自定义曲线映射"，不依赖 MATLAB 内置函数，完整展示从直方图计算到灰度映射的全过程。

Matlab 复制代码

% 直方图均衡化及自定义灰度映射实现
% 功能：对输入图像进行直方图均衡化，并对比不同自定义曲线（线性、对数、指数、S型）的效果
% 日期：2025-12-11

%% 1. 读取图像并转为灰度图
% 确保当前目录下有示例图像，这里以MATLAB自带的'pout.tif'（人像）为例
img = imread('pout.tif');
if size(img,3) == 3  % 如果是彩色图，转为灰度图
    img_gray = rgb2gray(img);
else
    img_gray = img;
end
[rows, cols] = size(img_gray);
total_pixels = rows * cols;  % 总像素数
gray_levels = 0:255;        % 灰度级范围

%% 2. 计算原始图像的直方图和累计分布函数（CDF）
% 计算直方图：统计每个灰度值的像素数量
hist_original = zeros(1, 256);
for i = 1:rows
    for j = 1:cols
        gray_val = img_gray(i,j) + 1;  % 索引从1开始（对应灰度0-255）
        hist_original(gray_val) = hist_original(gray_val) + 1;
    end
end

% 计算归一化直方图（概率密度）
pdf_original = hist_original / total_pixels;

% 计算累计分布函数（CDF）
cdf_original = zeros(1, 256);
cdf_original(1) = pdf_original(1);
for k = 2:256
    cdf_original(k) = cdf_original(k-1) + pdf_original(k);
end

%% 3. 实现标准直方图均衡化
% 计算映射关系：s = CDF(r) * 255（四舍五入取整）
map_equal = round(cdf_original * 255);

% 应用映射得到均衡化图像
img_equal = zeros(rows, cols, 'uint8');
for i = 1:rows
    for j = 1:cols
        gray_val = img_gray(i,j) + 1;  % 原灰度值（索引）
        img_equal(i,j) = map_equal(gray_val);
    end
end

% 计算均衡化后的直方图（用于可视化）
hist_equal = zeros(1, 256);
for i = 1:rows
    for j = 1:cols
        gray_val = img_equal(i,j) + 1;
        hist_equal(gray_val) = hist_equal(gray_val) + 1;
    end
end

%% 4. 实现自定义灰度曲线映射
% 自定义映射函数：输入原灰度（0-255），输出新灰度（0-255）
% 注意：所有映射需归一化到0-255范围，避免溢出

% （1）线性映射（对比基准，相当于无处理）
map_linear = gray_levels;  % 新灰度=原灰度

% （2）对数映射：增强暗部细节（参数c用于归一化）
c_log = 255 / log(1 + 255);  % 确保最大灰度映射到255
map_log = round(c_log * log(1 + gray_levels));

% （3）指数映射：增强亮部细节（参数gamma=1.5，gamma>1时亮部压缩、暗部拉伸）
gamma_exp = 1.5;
map_exp = round(255 * (gray_levels / 255).^gamma_exp);

% （4）S型曲线映射：增强对比度（结合log和exp的特性）
map_s = zeros(1, 256);
for k = 1:256
    r = (k-1) / 255;  % 归一化到0-1
    if r <= 0.5
        map_s(k) = round(127 * (2*r).^0.8);  % 暗部拉伸
    else
        map_s(k) = round(128 + 127 * (2*(1-r)).^0.8);  % 亮部压缩
    end
end

% 应用自定义映射
img_linear = apply_map(img_gray, map_linear);
img_log = apply_map(img_gray, map_log);
img_exp = apply_map(img_gray, map_exp);
img_s = apply_map(img_gray, map_s);

%% 5. 可视化结果
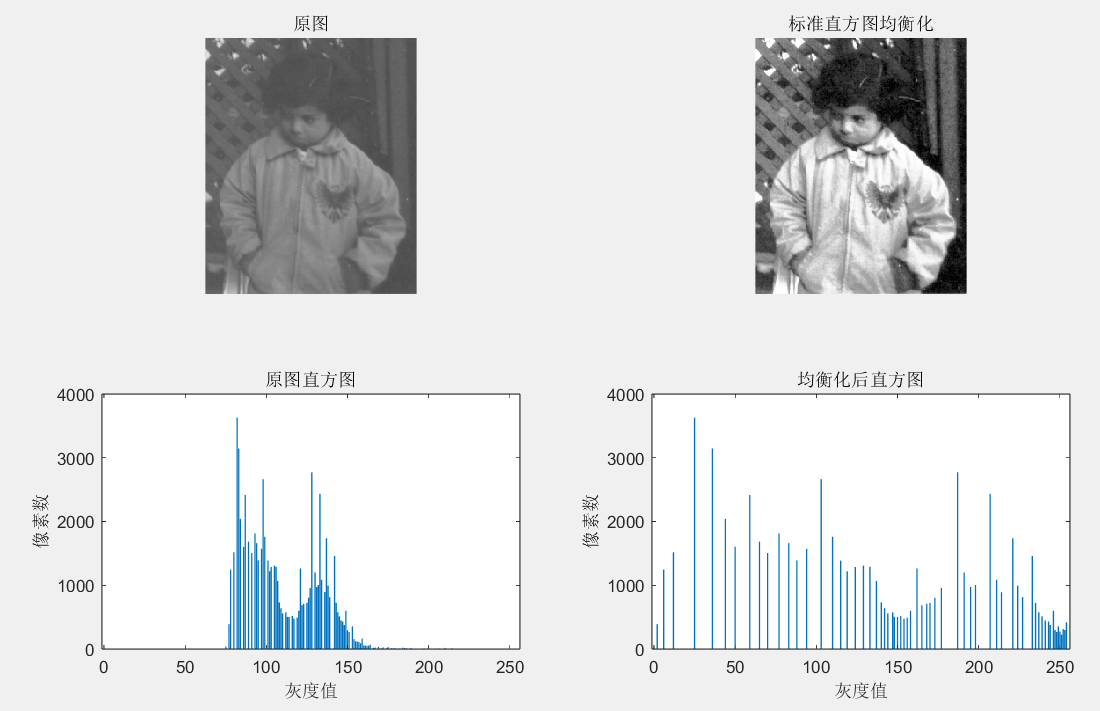
% 图1：原图与均衡化结果对比
figure('Name','原图与标准均衡化对比','Position',[100 100 1000 600]);
subplot(2,2,1); imshow(img_gray); title('原图');
subplot(2,2,2); imshow(img_equal); title('标准直方图均衡化');
subplot(2,2,3); bar(gray_levels, hist_original); title('原图直方图'); xlabel('灰度值'); ylabel('像素数');
subplot(2,2,4); bar(gray_levels, hist_equal); title('均衡化后直方图'); xlabel('灰度值'); ylabel('像素数');

% 图2：自定义曲线映射效果对比
figure('Name','自定义曲线映射效果','Position',[200 200 1200 800]);
subplot(2,2,1); imshow(img_linear); title('线性映射（原图）');
subplot(2,2,2); imshow(img_log); title('对数映射（增强暗部）');
subplot(2,2,3); imshow(img_exp); title('指数映射（增强亮部）');
subplot(2,2,4); imshow(img_s); title('S型映射（增强对比）');

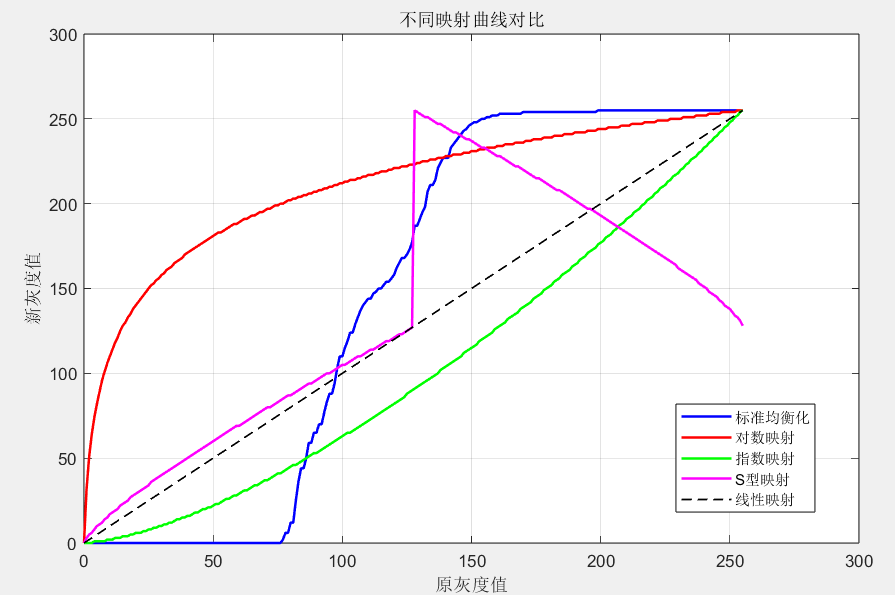
% 图3：各映射曲线对比
figure('Name','灰度映射曲线','Position',[300 300 800 500]);
plot(gray_levels, map_equal, 'b', 'LineWidth',1.5); hold on;
plot(gray_levels, map_log, 'r', 'LineWidth',1.5);
plot(gray_levels, map_exp, 'g', 'LineWidth',1.5);
plot(gray_levels, map_s, 'm', 'LineWidth',1.5);
plot(gray_levels, map_linear, 'k--', 'LineWidth',1);
legend('标准均衡化','对数映射','指数映射','S型映射','线性映射');
xlabel('原灰度值'); ylabel('新灰度值'); title('不同映射曲线对比'); grid on;

%% 6. 结果解读
disp('===== 结果解读 =====');
disp('1. 标准直方图均衡化：原图直方图若集中在某一区域，均衡化后会明显分散，图像对比度显著提升，但可能丢失部分氛围（如夜景变亮后失去暗调）；');
disp('2. 对数映射：低灰度区（暗部）被显著拉伸，适合增强阴影中的细节（如老照片的暗部纹理）；');
disp('3. 指数映射：高灰度区（亮部）被拉伸，适合修复过曝图像（如天空过白时找回云层细节）；');
disp('4. S型映射：暗部和亮部分别向两端拉伸，中间灰度压缩，适合需要增强立体感的场景（如人像、产品图）。');

%% 辅助函数：应用灰度映射（需放在脚本末尾）
function img_mapped = apply_map(img_gray, map)
    [rows, cols] = size(img_gray);
    img_mapped = zeros(rows, cols, 'uint8');
    for i = 1:rows
        for j = 1:cols
            gray_val = img_gray(i,j) + 1;  % 原灰度值（索引1-256）
            img_mapped(i,j) = map(gray_val);
        end
    end
end

运行说明

>> EQ

===== 结果解读 =====

标准直方图均衡化：原图直方图若集中在某一区域，均衡化后会明显分散，图像对比度显著提升，但可能丢失部分氛围（如夜景变亮后失去暗调）；

对数映射：低灰度区（暗部）被显著拉伸，适合增强阴影中的细节（如老照片的暗部纹理）；

指数映射：高灰度区（亮部）被拉伸，适合修复过曝图像（如天空过白时找回云层细节）；

S型映射：暗部和亮部分别向两端拉伸，中间灰度压缩，适合需要增强立体感的场景（如人像、产品图）。

>> EQ

===== 结果解读 =====

标准直方图均衡化：原图直方图若集中在某一区域，均衡化后会明显分散，图像对比度显著提升，但可能丢失部分氛围（如夜景变亮后失去暗调）；

对数映射：低灰度区（暗部）被显著拉伸，适合增强阴影中的细节（如老照片的暗部纹理）；

指数映射：高灰度区（亮部）被拉伸，适合修复过曝图像（如天空过白时找回云层细节）；

S型映射：暗部和亮部分别向两端拉伸，中间灰度压缩，适合需要增强立体感的场景（如人像、产品图）。

>>

确保 MATLAB 当前目录下有图像文件（可使用 'pout.tif'，MATLAB 自带；或替换为其他灰度图路径）；
直接运行脚本，将生成 3 个可视化窗口：原图与均衡化对比、自定义映射效果、映射曲线对比；
若图像为彩色图，脚本会自动转为灰度图处理。

🌈 终章：光影的哲学

直方图均衡化的本质，不是 "让所有灰度平等"，而是 "让每个灰度都有展现价值的空间"。就像生活中的资源分配，绝对平均未必是最优解，按需调整才能让整体焕发生机。

当技术懂得 "取舍"------ 在暗部多一分光亮，在亮部少一分锋芒，图像便有了呼吸感。这或许就是技术最美的样子：它用数学的严谨计算，实现了艺术般的平衡，让每一个像素都成为故事的讲述者。

下一次翻看老照片时，不妨试试用直方图均衡化与时光对话 ------ 那些被光影掩埋的细节，或许正等着被重新唤醒。