milliLoc 论文精读:把商用毫米波 FMCW 的绝对测距从"厘米栅格"推进到"毫米级连续值",并顺带修正 AoA 的系统相位偏差
Guidong Zhang, Guoxuan Chi, Yi Zhang, Xuan Ding, and Zheng Yang. 2023. Push the Limit of Millimeter-wave Radar Localization. ACM Trans. Sen. Netw. 19, 3, Article 59 (August 2023), 21 pages.
这篇论文最值得反复读的地方并不在"毫米波 FMCW 能测距"这件事本身,而在于作者抓住了一个常常被当作"信号处理常识、只能接受"的低层瓶颈:DFT 频谱是离散采样的,真实拍频落在 bin 之间时,峰值 bin 的选择会把一个连续区间压成同一个输出,于是距离被量化到一个约 4 cm 的 range bin 中;更隐蔽的是,同样的采样误差还会把"峰点相位"推离真实初相,污染 AoA。
milliLoc 的核心手段非常"低层":不加带宽、不加采样率,而是把 DFT 峰附近的多个复数采样点当作观测,用一个严格的解析模型去拟合它们,反推拍频的"亚 bin 偏移"以及每个分量的复幅度,从而把距离从 bin 级恢复为连续值,并用复幅度的相位直接作为初相来算 AoA。
1. 从图 1 开始:频谱采样误差为什么会同时伤害距离与 AoA
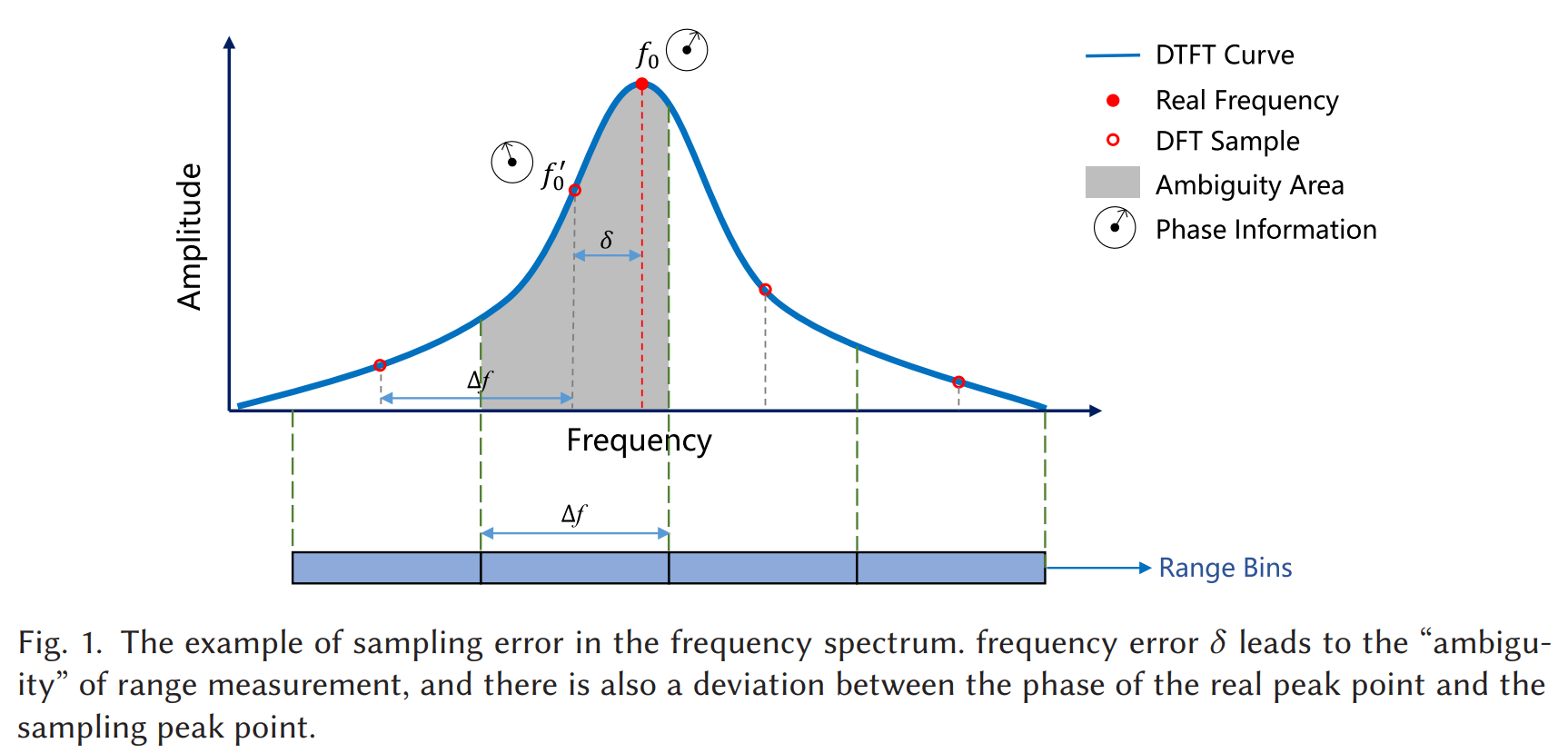
论文一上来就用 Fig.1 把关键矛盾画出来:蓝色是连续频谱,红点是 DFT 的离散采样点。真实峰值在连续频率 f0f_0f0 处,但我们只能在离散点里选最大值,于是把它当成 f^0\hat f_0f^0,产生频率误差 δ\deltaδ。这带来两件事:频率上出现"ambiguity area",距离上出现 range bin;此外,真实峰值点的相位 与采样峰值点的相位也不一致,从而 AoA 计算会偏。
用一句话描述:
真正想要的是"连续频率参数",但只观测到了"在离散频点上的复数采样"。如果只取一个点(峰点),就必然丢掉亚 bin 信息;如果利用多个点的形状,就可能把连续参数拟合回来。
论文把这条路线称为更偏"super frequency resolution",并强调它与 MUSIC/ESPRIT 一类主要做"super spatial resolution"的思路不同:后者更关注多径可分辨性,前者直击频率估计的低层误差。
2. FMCW 的基础链条:chirp → IF 拍频 → 距离分辨率 Δd=c2B\Delta d=\frac{c}{2B}Δd=2Bc
2.1 发射 chirp 与回波延迟
发射信号(线性调频 chirp)写为
STx(t)=cos (2πf0t+πBTct2)(1) S_{Tx}(t)=\cos\!\left(2\pi f_0 t+\frac{\pi B}{T_c}t^2\right)\tag{1} STx(t)=cos(2πf0t+TcπBt2)(1)
它的瞬时频率是
f(t)=f0+BTct f(t)=f_0+\frac{B}{T_c}t f(t)=f0+TcBt
目标距离为 ddd,往返传播时延
τ=2dc \tau=\frac{2d}{c} τ=c2d
接收信号视为延迟版本:
SRx(t)=α STx(t−τ)=α STx (t−2dc)(2) S_{Rx}(t)=\alpha\,S_{Tx}(t-\tau)=\alpha\,S_{Tx}\!\left(t-\frac{2d}{c}\right)\tag{2} SRx(t)=αSTx(t−τ)=αSTx(t−c2d)(2)
2.2 混频得到 IF:拍频与距离成正比
混频器将 STx(t)S_{Tx}(t)STx(t) 与 SRx(t)S_{Rx}(t)SRx(t) 相乘并低通,得到 IF 信号(论文给出结果式):
SIF(t)=α^cos (4πBdcTc t+ϕ0)(3) S_{IF}(t)=\hat{\alpha}\cos\!\left(\frac{4\pi Bd}{cT_c}\,t+\phi_0\right)\tag{3} SIF(t)=α^cos(cTc4πBdt+ϕ0)(3)
因此 IF 的拍频为
fb=12π⋅4πBdcTc=2BdcTc⇒d=cTc2Bfb f_b=\frac{1}{2\pi}\cdot\frac{4\pi Bd}{cT_c}=\frac{2Bd}{cT_c} \quad\Rightarrow\quad d=\frac{cT_c}{2B}f_b fb=2π1⋅cTc4πBd=cTc2Bd⇒d=2BcTcfb
2.3 DFT 的频率分辨率把距离锁在厘米级
对长度为 TcT_cTc 的观测窗,DFT 频率分辨率是
Δf=1Tc \Delta f = \frac{1}{T_c} Δf=Tc1
把 fb=2BdcTcf_b=\frac{2Bd}{cT_c}fb=cTc2Bd 代进去,频率分辨率对应的距离分辨率满足
Δf=2BcTcΔd⇒Δd=c2B(4) \Delta f=\frac{2B}{cT_c}\Delta d \quad\Rightarrow\quad \Delta d=\frac{c}{2B}\tag{4} Δf=cTc2BΔd⇒Δd=2Bc(4)
这条式子就是"只要带宽 BBB 不变,距离分辨率就被卡死"的根源。论文用 77--81 GHz、约 4 GHz 带宽的商用设备举例,Δd\Delta dΔd 约为 4 cm,因此同一 range bin 内的目标都会输出同一个距离,形成距离模糊。
对应的 chirp 示意在 Fig.2:
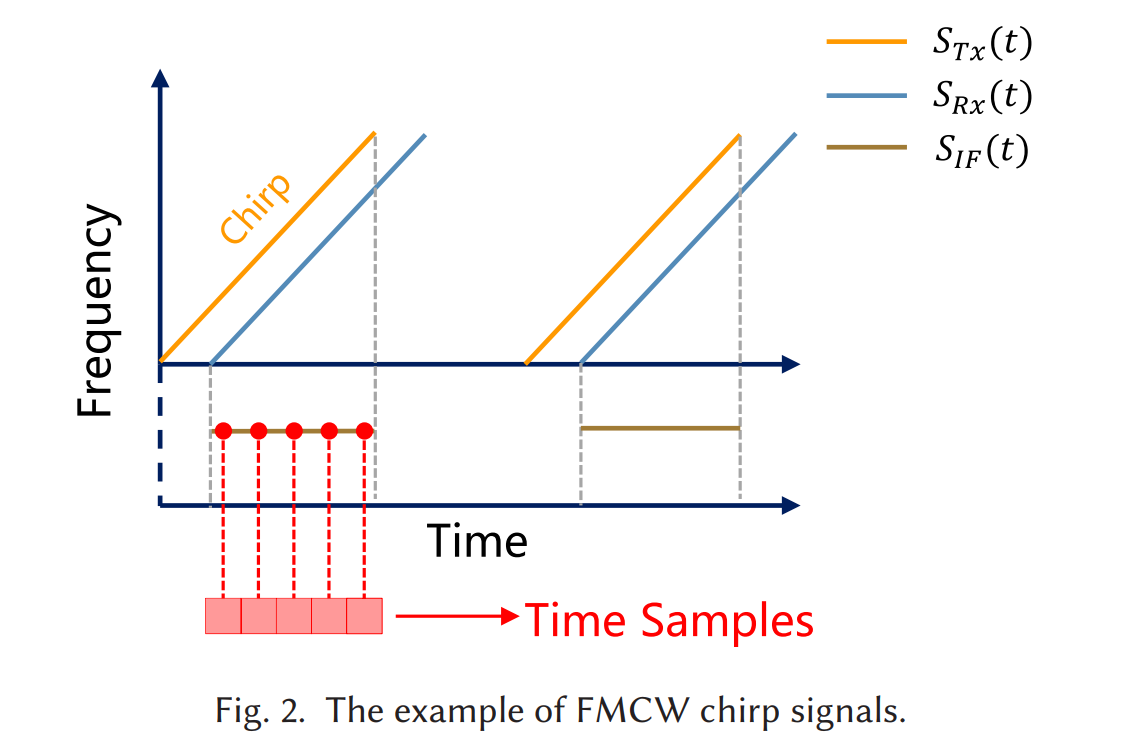
3. 把"采样误差"参数化:δ\deltaδ 是贯穿全文的关键隐变量
论文用一个建模把问题钉死在 δ\deltaδ 上:假设真实归一化频率是
f=kp+δN,δ∈[−12,12] f=\frac{k_p+\delta}{N}, \qquad \delta\in\left[-\frac12,\frac12\right] f=Nkp+δ,δ∈[−21,21]
其中 kpk_pkp 是 DFT 中幅度最大的 bin(传统方法能得到的),δ\deltaδ 是真实频率相对这个 bin 的亚 bin 偏移(传统方法丢掉的)。
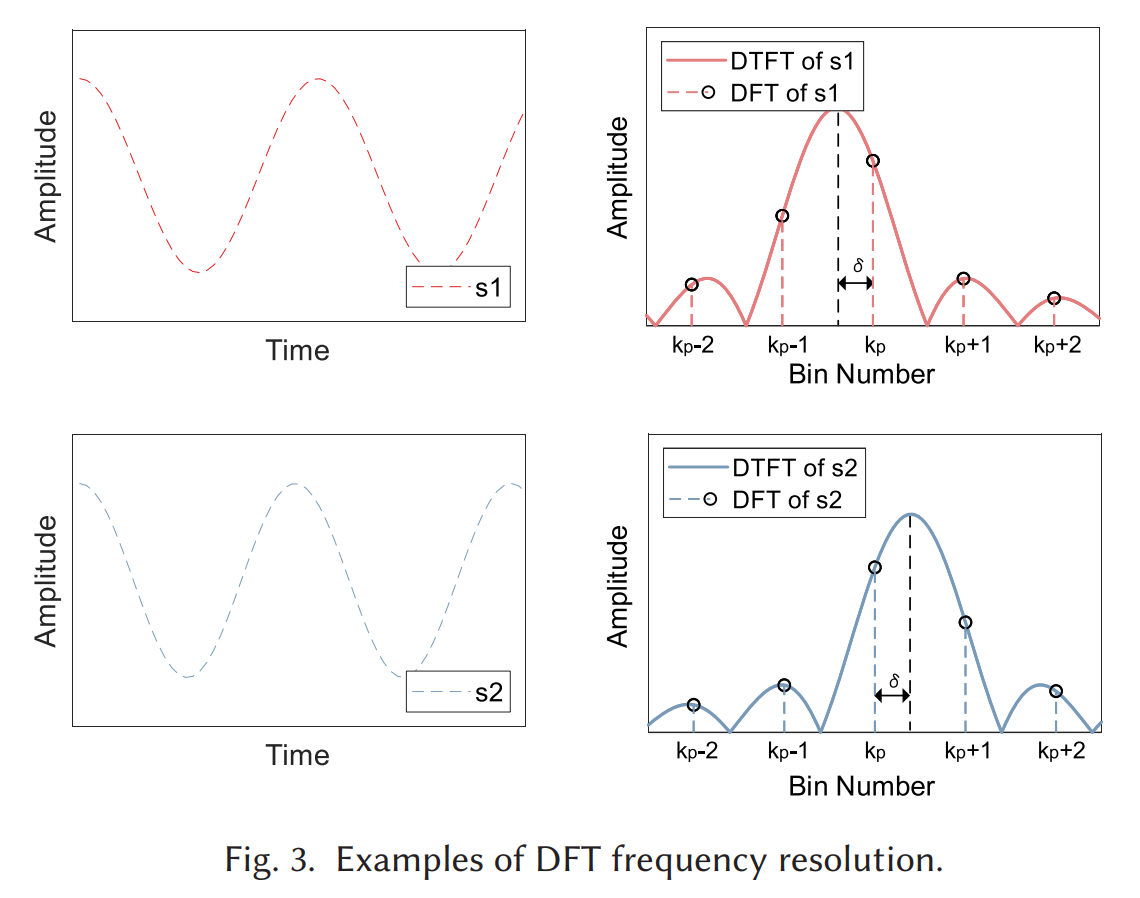
接着作者用 Fig.3 举例:两个信号 s1,s2s_1,s_2s1,s2 的真实频率分别是 kp−δN\frac{k_p-\delta}{N}Nkp−δ 与 kp+δN\frac{k_p+\delta}{N}Nkp+δ,尽管不同,但峰值 bin 都落在 kpk_pkp,于是传统峰点法会判为相同;然而它们在 kp−1,kp,kp+1k_p-1,k_p,k_p+1kp−1,kp,kp+1 的幅度分布并不相同,这正是可被利用的信息。
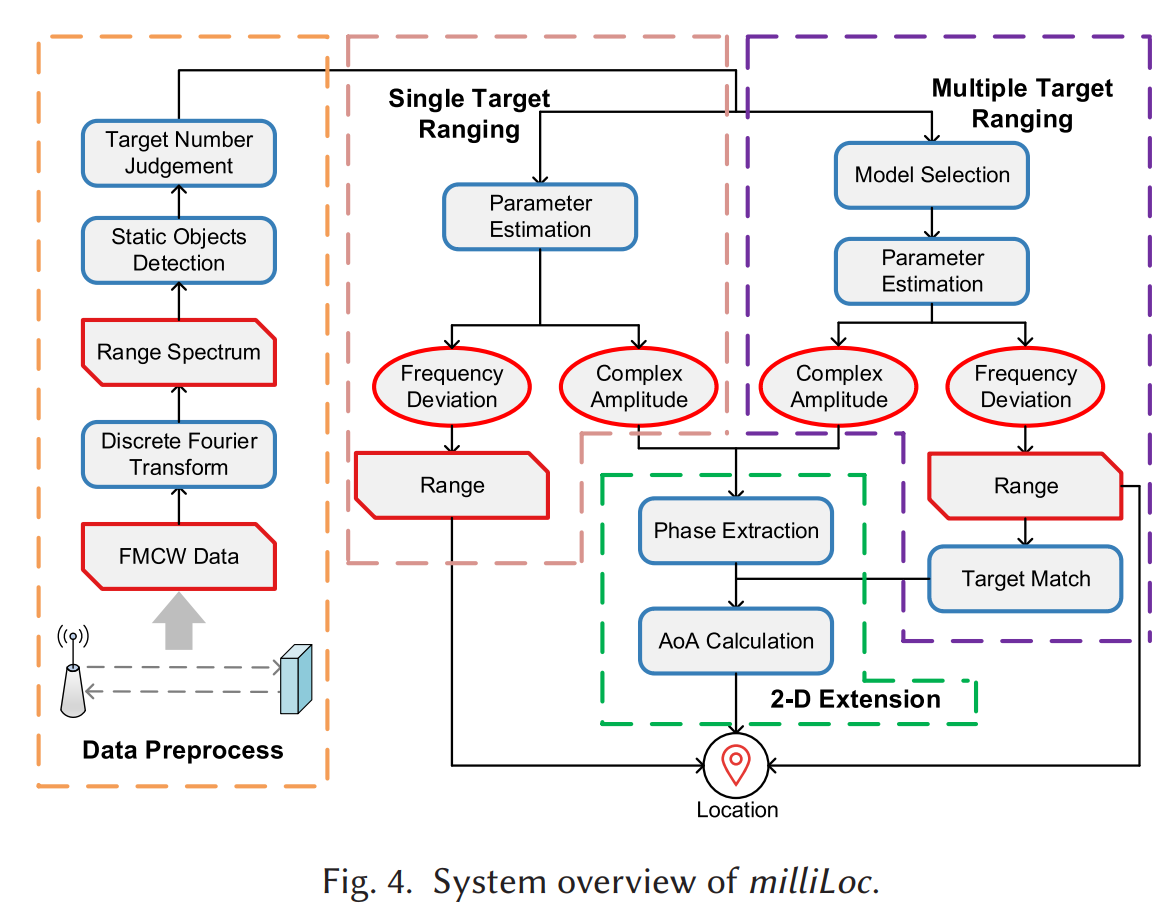
同一页还有 Fig.4 的系统总览图:预处理得到 range spectrum;先做静态物体影响抑制;再分单目标/多目标的测距;最后用复幅度信息改进 AoA 并做 2D 定位。
4. 核心算法一:单目标谱峰重构(从多个 DFT 样本拟合出 δ\deltaδ 与复幅度)
4.1 单频复指数模型:把一个目标当作一个频率分量
单目标时,回波 IF 里主要对应一个频率分量。离散化后,可以把信号写成
r[n]=A0ejθ0ej2πfn+w[n],n=0,1,...,N−1(5) r[n]=A_0e^{j\theta_0}e^{j2\pi fn}+w[n], \quad n=0,1,\dots,N-1\tag{5} r[n]=A0ejθ0ej2πfn+w[n],n=0,1,...,N−1(5)
其中 A0ejθ0A_0e^{j\theta_0}A0ejθ0 是未知复幅度(幅值 A0A_0A0、初相 θ0\theta_0θ0),w[n]w[n]w[n] 是白噪声,归一化频率 f=kp+δNf=\frac{k_p+\delta}{N}f=Nkp+δ。
对 r[n]r[n]r[n] 做 DFT:
R[k]=∑n=0N−1r[n]e−j2πNnk(6) R[k]=\sum_{n=0}^{N-1}r[n]e^{-j\frac{2\pi}{N}nk}\tag{6} R[k]=n=0∑N−1r[n]e−jN2πnk(6)
kpk_pkp 被假设为幅度最大的 bin,于是未知量落在三个实参数:A0,θ0,δA_0,\theta_0,\deltaA0,θ0,δ。
4.2 解析表达式:DFT 系数是一个几何级数(Dirichlet 核)
关键结果如下(把 kkk 写成 kp−mk_p-mkp−m):
R[kp−m]=A0ejθ01−ej2π(δ+m)1−ej2πN(δ+m)+W[kp−m](7) R[k_p-m] =A_0e^{j\theta_0} \frac{1-e^{j2\pi(\delta+m)}}{1-e^{j\frac{2\pi}{N}(\delta+m)}} + W[k_p-m]\tag{7} R[kp−m]=A0ejθ01−ejN2π(δ+m)1−ej2π(δ+m)+W[kp−m](7)
这里的分式是"有限长复指数"在 DFT 网格上的闭式表达,它决定了谱峰附近每个 bin 的幅度与相位如何随 δ\deltaδ 变化。直觉上:δ\deltaδ 越接近 0,峰越集中在 kpk_pkp;δ\deltaδ 越偏离 0,泄漏形状越不对称,于是 kp−1,kp,kp+1k_p-1,k_p,k_p+1kp−1,kp,kp+1 的相对关系会改变。
4.3 一个 DFT 样本能提供两条方程:信息量来自"复数"
因为 R[k]R[k]R[k] 是复数,取实部和虚部可以得到两条实方程。可以把它写成
ℜ{R[kp−m]}=ℜ{A0ejθ01−ej2π(δ+m)1−ej2πN(δ+m)+W[kp−m]}ℑ{R[kp−m]}=ℑ{A0ejθ01−ej2π(δ+m)1−ej2πN(δ+m)+W[kp−m]}(8) \begin{aligned} \Re\{R[k_p-m]\} &= \Re\left\{A_0e^{j\theta_0}\frac{1-e^{j2\pi(\delta+m)}}{1-e^{j\frac{2\pi}{N}(\delta+m)}} + W[k_p-m]\right\}\\ \Im\{R[k_p-m]\} &= \Im\left\{A_0e^{j\theta_0}\frac{1-e^{j2\pi(\delta+m)}}{1-e^{j\frac{2\pi}{N}(\delta+m)}} + W[k_p-m]\right\} \end{aligned}\tag{8} ℜ{R[kp−m]}ℑ{R[kp−m]}=ℜ{A0ejθ01−ejN2π(δ+m)1−ej2π(δ+m)+W[kp−m]}=ℑ{A0ejθ01−ejN2π(δ+m)1−ej2π(δ+m)+W[kp−m]}(8)
因此理论上至少需要两个 DFT 采样点(给四条实方程)才有希望稳健地解出三个未知实参数。
4.4 把"解方程"变成"拟合":非线性最小二乘
由此,该论文把求解转成优化问题。用若干个选定的 DFT 采样点 k∈{K1,...,KM}k\in\{K_1,\dots,K_M\}k∈{K1,...,KM},最小化模型与观测的差:
min(A0,θ0,δ)⟨R[k]−A0ejθ01−ej2π(δ+kp−k)1−ej2πN(δ+kp−k)⟩(9) \min_{(A_0,\theta_0,\delta)} \left\langle R[k]- A_0e^{j\theta_0} \frac{1-e^{j2\pi(\delta+k_p-k)}}{1-e^{j\frac{2\pi}{N}(\delta+k_p-k)}} \right\rangle\tag{9} (A0,θ0,δ)min⟨R[k]−A0ejθ01−ejN2π(δ+kp−k)1−ej2π(δ+kp−k)⟩(9)
其中 ⟨⋅⟩\langle\cdot\rangle⟨⋅⟩ 表示对实部或虚部分别做拟合(等价于把复残差展开成实向量)。
紧接着,作者指出一个事实如下:远离峰值的 bin 幅度小、相对噪声大,如果它们在优化中权重相同,会拖坏解。于是加入"幅度调制"(更准确说是加权):
min(A0,θ0,δ)∣R[k]∣⟨R[k]−A0ejθ01−ej2π(δ+kp−k)1−ej2πN(δ+kp−k)⟩(10) \min_{(A_0,\theta_0,\delta)} |R[k]| \left\langle R[k]- A_0e^{j\theta_0} \frac{1-e^{j2\pi(\delta+k_p-k)}}{1-e^{j\frac{2\pi}{N}(\delta+k_p-k)}} \right\rangle\tag{10} (A0,θ0,δ)min∣R[k]∣⟨R[k]−A0ejθ01−ejN2π(δ+kp−k)1−ej2π(δ+kp−k)⟩(10)
也就是用 ∣R[k]∣|R[k]|∣R[k]∣ 让高幅度点贡献更大、低幅度点贡献更小。求解方法使用 Levenberg--Marquardt(LM)这类非线性最小二乘常用算法。
4.5 从 (kp,δ)(k_p,\delta)(kp,δ) 回到距离:δ\deltaδ 直接决定"bin 内位置"
得到更精确的归一化频率 kp+δN\frac{k_p+\delta}{N}Nkp+δ 后,论文给出距离公式:
d=kp+δN⋅cFsTc2B(11) d=\frac{k_p+\delta}{N}\cdot\frac{cF_sT_c}{2B}\tag{11} d=Nkp+δ⋅2BcFsTc(11)
这里 FsF_sFs 是采样率。可以把它理解成:传统峰点法是用 kpk_pkp 来算距离;milliLoc 则用 kp+δk_p+\deltakp+δ 来算距离,δ\deltaδ 就是"把一个 4 cm 的 bin 切成很多细份"的连续坐标。
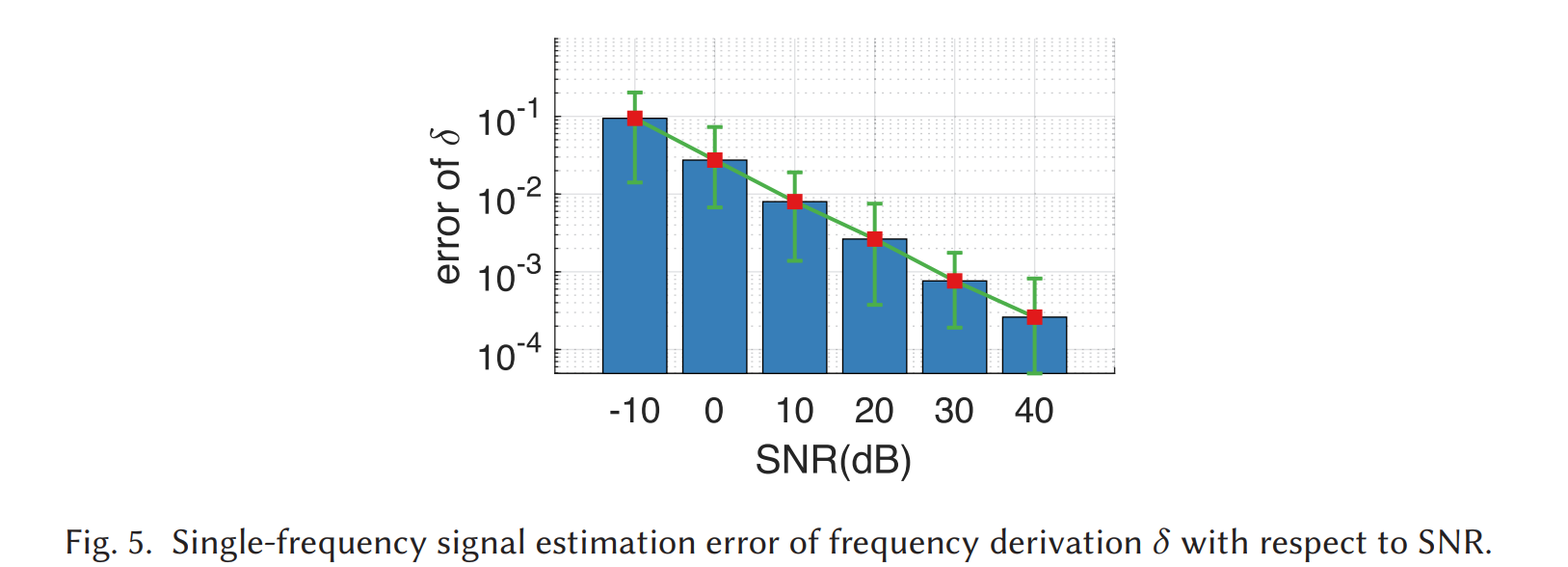
4.6 仿真图 5 的量级含义:δ\deltaδ 误差 0.01 就是亚毫米量级
论文在仿真中用单频 + 白噪声,展示了 δ\deltaδ 的估计误差随 SNR 的下降趋势,并强调:SNR=10 dB 时 δ\deltaδ 的中位误差约 0.01,而在 4 cm/bin 的情况下,这意味着约 0.01×4 cm=0.4 mm0.01\times 4\text{ cm}=0.4\text{ mm}0.01×4 cm=0.4 mm 的中位测距误差(理想条件)。
5. 核心算法二:多目标时如何"分开"叠加谱峰,以及为什么出现"12 cm"这个门槛
5.1 双目标模型:频域上是两个 Dirichlet 核的叠加
两目标对应双频模型:
t[n]=A1ejθ1ej2πf1n+A2ejθ2ej2πf2n+w[n](12) t[n]=A_1e^{j\theta_1}e^{j2\pi f_1n}+A_2e^{j\theta_2}e^{j2\pi f_2n}+w[n]\tag{12} t[n]=A1ejθ1ej2πf1n+A2ejθ2ej2πf2n+w[n](12)
其中 f1=kp1+δ1N, f2=kp2+δ2Nf_1=\frac{k_{p1}+\delta_1}{N},\ f_2=\frac{k_{p2}+\delta_2}{N}f1=Nkp1+δ1, f2=Nkp2+δ2。未知量从 3 个实参数变成 6 个实参数。
5.2 两种情况:峰分开就分别拟合,峰挤在一起就联合拟合
论文给出一个很实用的分流规则:
当 ∣kp1−kp2∣>3|k_{p1}-k_{p2}|>3∣kp1−kp2∣>3 时,两个峰相距较远,互扰较小,可以分别按单目标算法拟合;当 ∣kp1−kp2∣≤3|k_{p1}-k_{p2}|\le 3∣kp1−kp2∣≤3 时,两个峰会"搅在一起",分别拟合会互相污染,于是要把两分量放到同一个优化问题里联合求解。
为什么 "3 个 bin" 会对应 "12 cm"?因为单 bin 的距离宽度约 4 cm,3 个 bin 约 12 cm,作者用它作为"峰是否明显分离"的经验阈值。
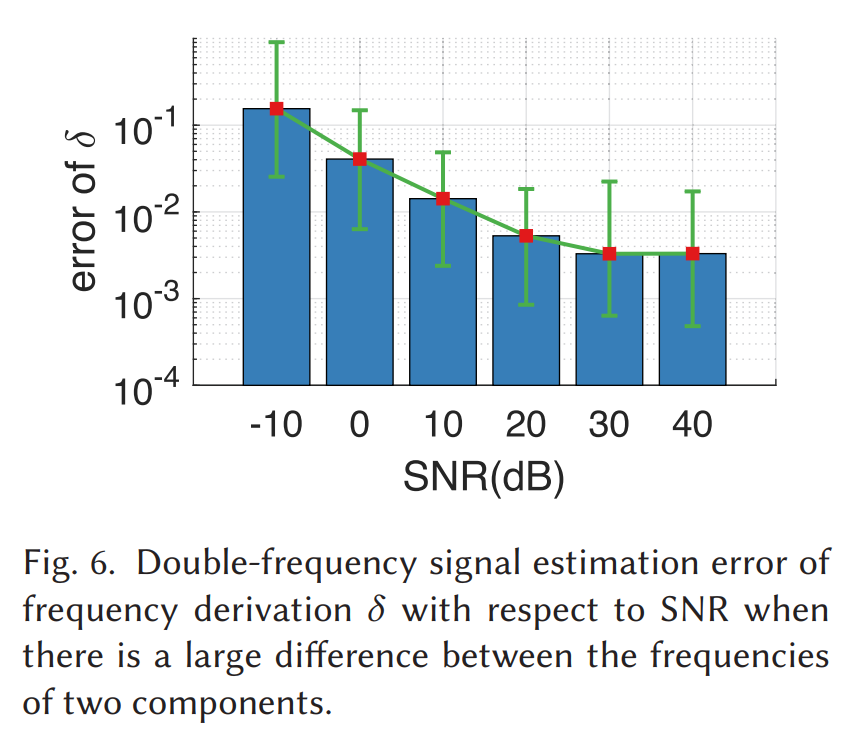
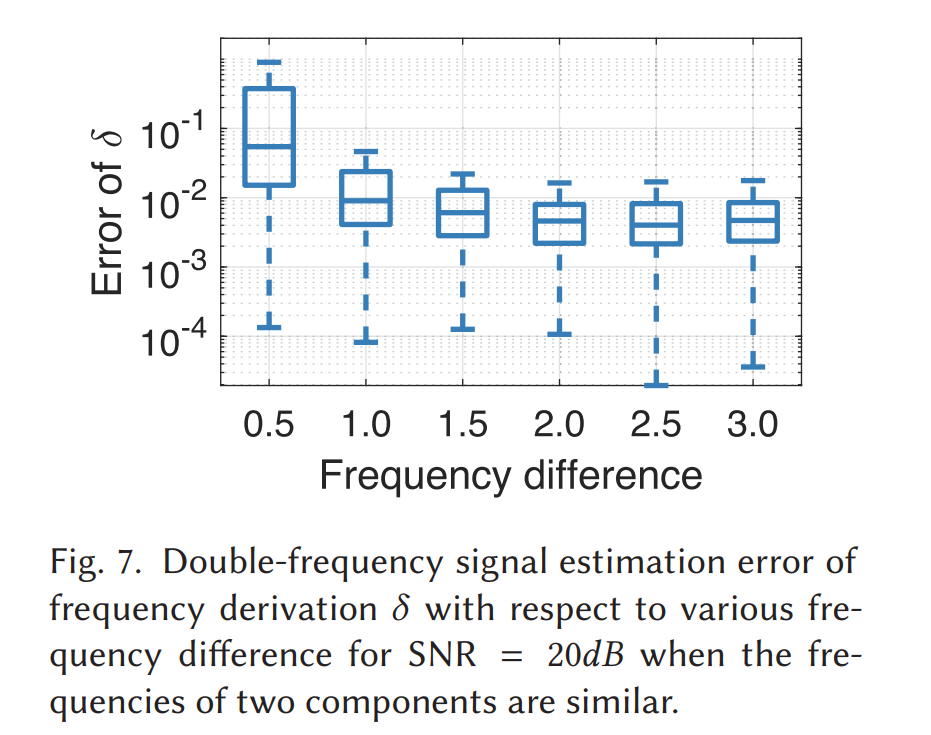
多目标仿真结果在 Fig.6 和 Fig.7。Fig.6 表示峰分离时误差随 SNR 的情况;Fig.7 固定 SNR=20 dB,展示当归一化频差变小(峰更近)时,估计偏差会迅速变大,直到无法分离。
6. 核心算法三:AoA 的"相位偏差"从哪里来,以及 milliLoc 如何修正
6.1 线阵 AoA 的基本式:相邻天线相位差
接收阵列为 ULA,相邻天线间距 d0d_0d0,入射角 θ\thetaθ。相邻天线的路程差 Δd=d0sinθ\Delta d=d_0\sin\thetaΔd=d0sinθ,于是相位差
Φ=2πd0sinθλ(13) \Phi=\frac{2\pi d_0\sin\theta}{\lambda}\tag{13} Φ=λ2πd0sinθ(13)
这就是 AoA 的基本测量方程。
6.2 传统"峰点相位=初相"什么时候成立:只有 δ=0\delta=0δ=0 才成立
很多工程实现会用 DFT 峰点的相位作为该频率分量的初相。论文把这种近似写成(忽略 δ\deltaδ 和噪声):
∠R[k]={θ0,k=kp0,k≠kp(14) \angle R[k]= \begin{cases} \theta_0, & k=k_p\\ 0, & k\ne k_p \end{cases}\tag{14} ∠R[k]={θ0,0,k=kpk=kp(14)
Fig.9(a)(b) 就是 δ=0\delta=0δ=0 的例子:时域信号的初相可以从峰点相位直接读出来;Fig.9©(d) 则展示 δ≠0\delta\neq 0δ=0 时峰点相位不再等于初相。
6.3 当 δ≠0\delta\neq 0δ=0 时,峰点相位会多出一个系统项 ∠(F(δ))\angle(F(\delta))∠(F(δ))
给出关键关系:
∠R[kp]=θ0+∠(F(δ))(15) \angle R[k_p]=\theta_0+\angle(F(\delta))\tag{15} ∠R[kp]=θ0+∠(F(δ))(15)
其中
F(δ)=1−ej2πδ1−ej2πNδ,−12≤δ≤12 F(\delta)=\frac{1-e^{j2\pi\delta}}{1-e^{j\frac{2\pi}{N}\delta}}, \qquad -\frac12\le\delta\le\frac12 F(δ)=1−ejN2πδ1−ej2πδ,−21≤δ≤21
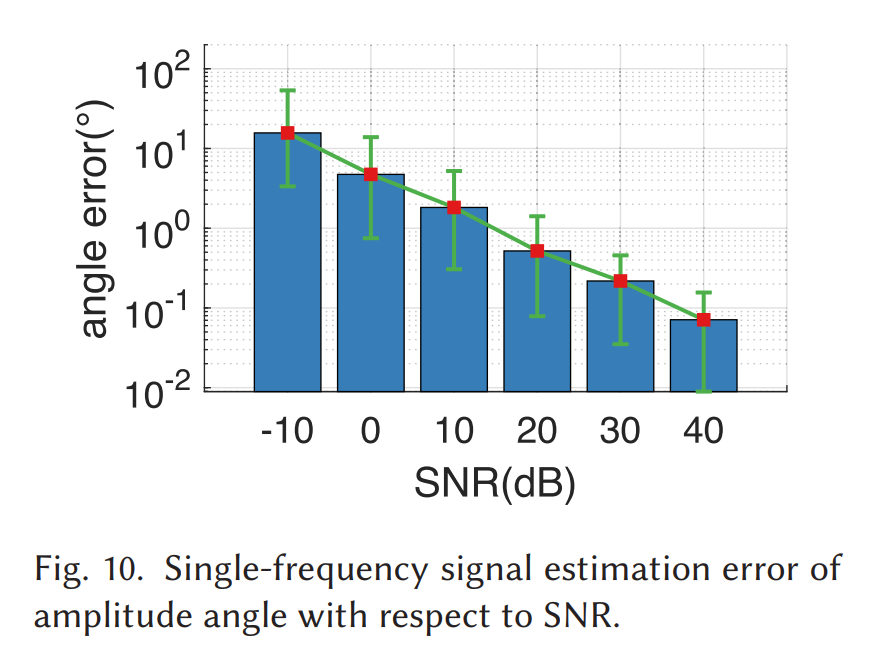
它的含义非常直接:从峰点读到的相位其实是"真实初相 + 一个由 δ\deltaδ 决定的附加相位"。只要 δ\deltaδ 不是整数(基本不会是),这个附加相位就不为 0,于是 AoA 会出现系统偏差。这一点对应 Fig.10:论文用仿真展示通过谱峰重构估计出的初相 θ0\theta_0θ0 误差随 SNR 的变化,SNR>20 dB 时中位角误差 < 1∘1^\circ1∘。
6.4 milliLoc 的修正方式:不用峰点相位,直接用拟合得到的 θ0\theta_0θ0
谱峰重构在求 δ\deltaδ 的同时会求出复幅度 A0ejθ0A_0e^{j\theta_0}A0ejθ0,于是 AoA 计算不再需要"从峰点相位读初相",而是直接取拟合出来的 θ0\theta_0θ0 作为每根天线对该频率分量的初相,再用式(13)做相位差求角度;多目标时,先按距离把不同天线上的目标匹配起来,再计算 AoA,最后由距离 + AoA 得到 2D 位置。
7. 实现细节与实验环境:为什么用小车绑盒子、为什么 50 Hz

论文实现平台是 TI IWR1443BOOST + DCA1000EVM。配置上,Tx1 发 77--81 GHz FMCW,Rx1--Rx4 接收,chirp 时长 Tc=60 μsT_c=60\,\mu sTc=60μs,每个 chirp 采样点数 N=256N=256N=256,对应最大探测距离 10.2 m;数据通过 DCA1000EVM 实时抓取;用 LiDAR 做地面真值;帧率设置为 50 Hz(每 0.02 s 输出一次定位)。
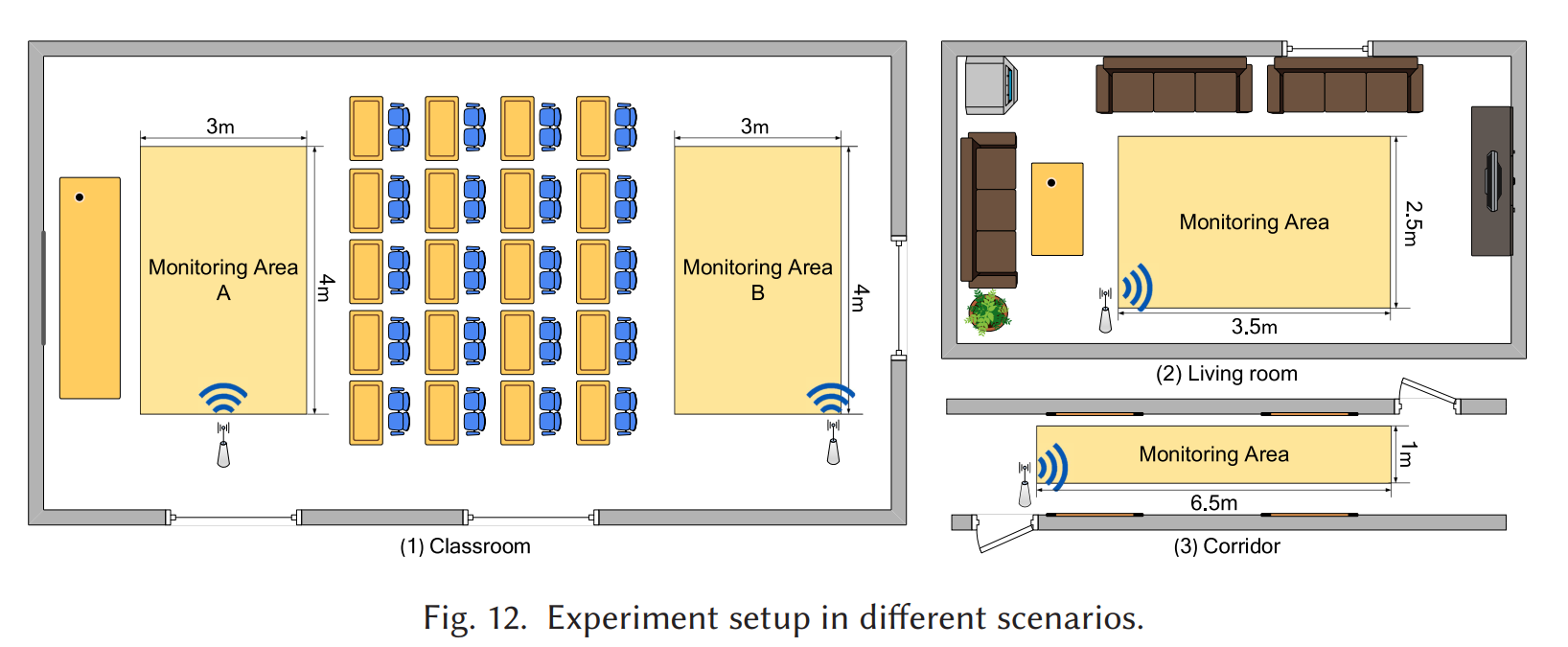
实验场景选了三种典型环境:空旷教室、家具较多客厅、狭窄走廊(Fig.12)。之所以不用人体做真值,是因为人体表面曲率复杂、多部位反射,难获得毫米级真值,所以用不同盒子绑在遥控小车上,通过小车轨迹得到更可对齐的参考。
8. 结果:不仅是"误差更小",更是"误差形状变了"
8.1 单目标正前方:从峰点法的毫米级"偶然好"到谱峰重构的毫米级"稳定好"
单目标、AoA<5° 时,论文报告 milliLoc 的中位定位误差 5.5 mm;peak-pt、PDA、GPR 分别为 11.1 mm、10.2 mm、11.8 mm。更值得注意的是误差分布(CDF)的整体左移:这通常意味着误差不是少数点改善,而是整体概率意义上的改善。
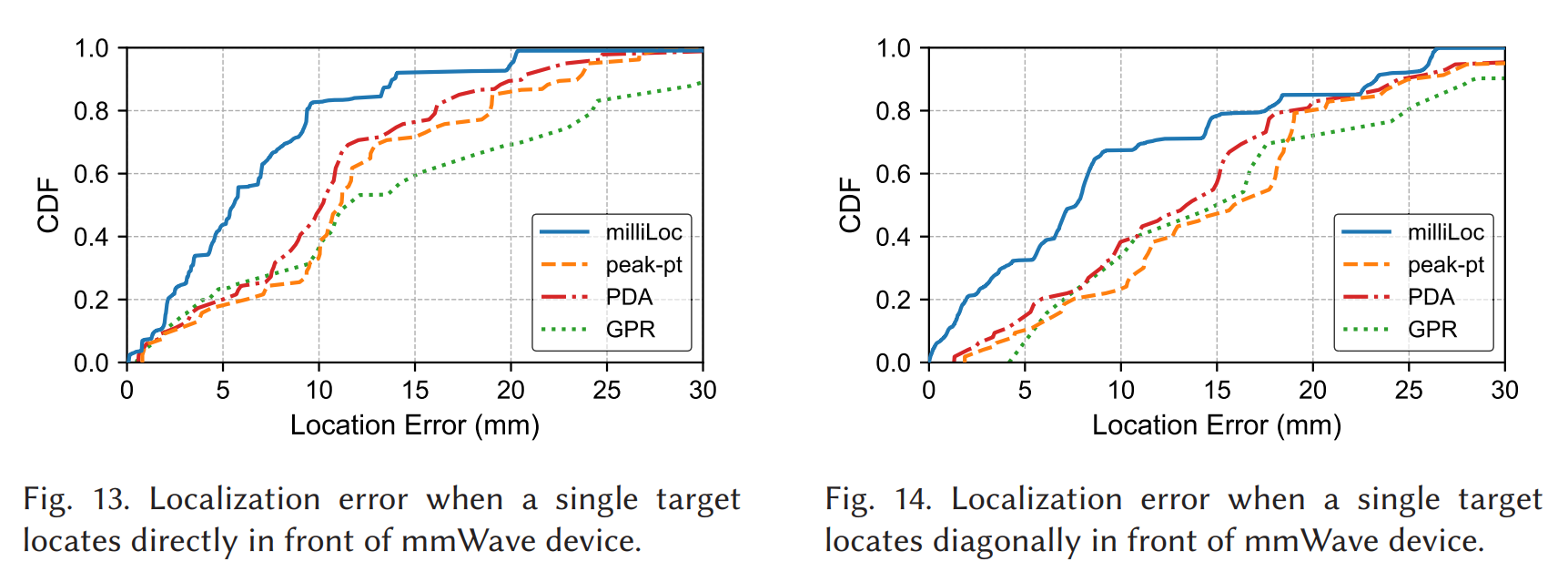
这一页的正文里还有一个很漂亮的"峰点法理论误差"估算:range bin 宽约 4 cm,若目标在 bin 内均匀分布,则误差近似均匀分布在 0--2 cm,中位误差约 1 cm,这与实验里 peak-pt 的 11.1 mm 量级吻合。
8.2 单目标斜前方:AoA 变大时所有方法都会退化,但 milliLoc 仍最好
当目标斜前方(AoA>5°)时,milliLoc 误差约 7.6 mm,peak-pt/PDA/GPR 约 15.7/13.4/14.9 mm。论文给出的物理解释是镜面反射:毫米波波长较短、目标表面相对更"光滑",入射角变大时反射能量偏向镜像方向,而商用雷达阵列孔径小,只有接近法线入射时反射才更可能被接收;AoA 增大导致接收信号衰减、噪声占比上升、非线性拟合更难,因此所有方法都会退化,但 milliLoc 仍表现最好。
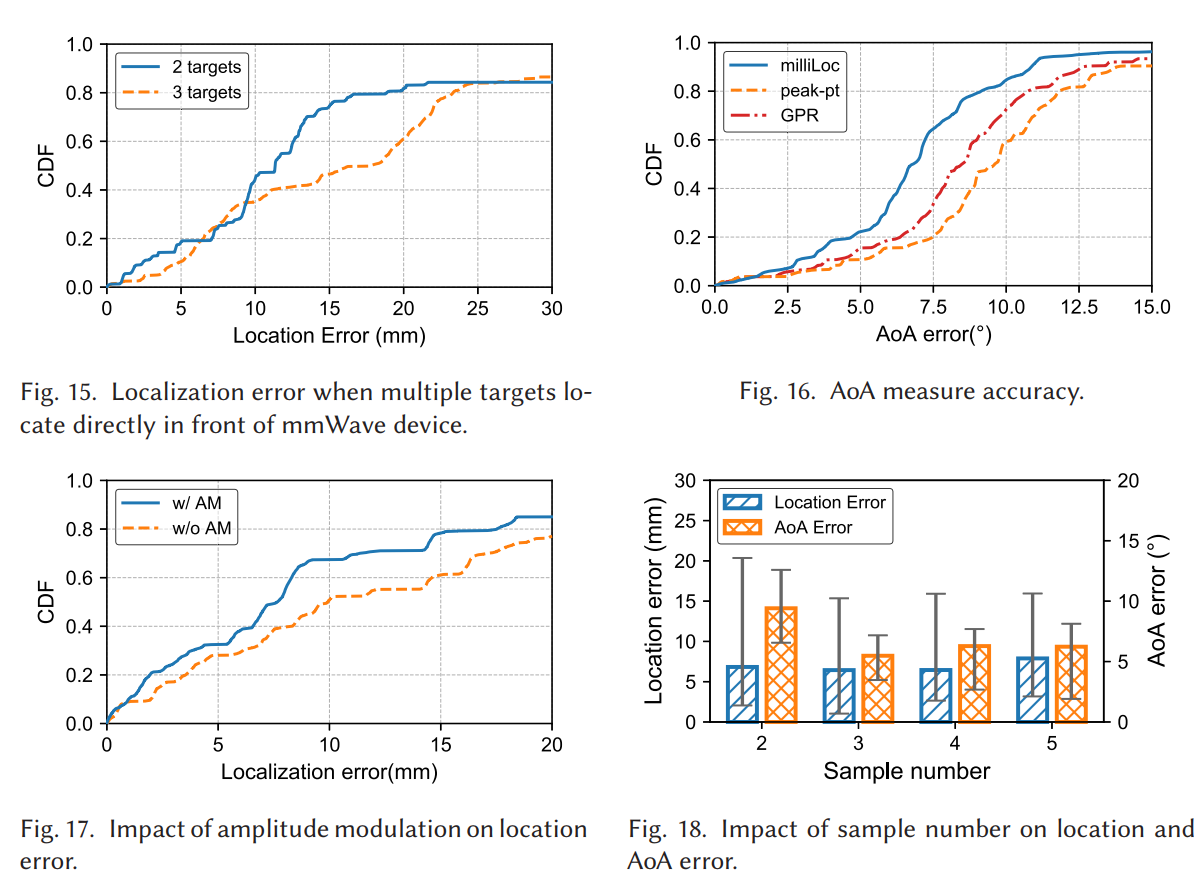
8.3 多目标:目标数越多,互扰越强,但仍保持毫米到厘米前段
两目标、三目标正前方时,中位误差约 11.3 mm 与 17.7 mm。误差上升的原因主要是频谱互扰与某些目标反射变弱。
8.4 AoA:提升的关键不是更复杂的空间谱,而是"把初相修正对了"
AoA 上,milliLoc 中位误差 6.6°,peak-pt 9.6°,GPR 8.5°,相对降低分别约 31.2% 与 22.3%。论文强调:在天线数量有限、热噪声与多径存在的情况下,单靠空间超分辨增强 AoA 的收益有限;milliLoc 的收益来自"通过拟合得到复幅度,从而修正每根天线的初相",无需增加阵列规模。
这些对比集中在 Fig.15--Fig.18:
9. 参数研究:为什么"3 个采样点 + 幅度加权"是甜点区
Fig.17 显示,如果去掉幅度加权(AM),中位误差会上升到 9.9 mm;加入 AM 后误差下降约 23.2%。这和式(10) 的含义一致:远离峰值的点幅度低、噪声相对大,给它更小权重能让拟合更稳。
Fig.18 讨论采样点数:理论上两点就可解三参数,但抗噪性差;点数太多又会把更多低幅度点拉进来,反而略增误差且增加计算量。实验显示 3 个点最合适。
接下来 Fig.19--Fig.20 讨论距离与 AoA 的影响,距离从 1--5 m 保持毫米级中位误差;AoA 超过约 20° 后误差陡增,这与前面镜面反射导致信噪比下降的解释一致。
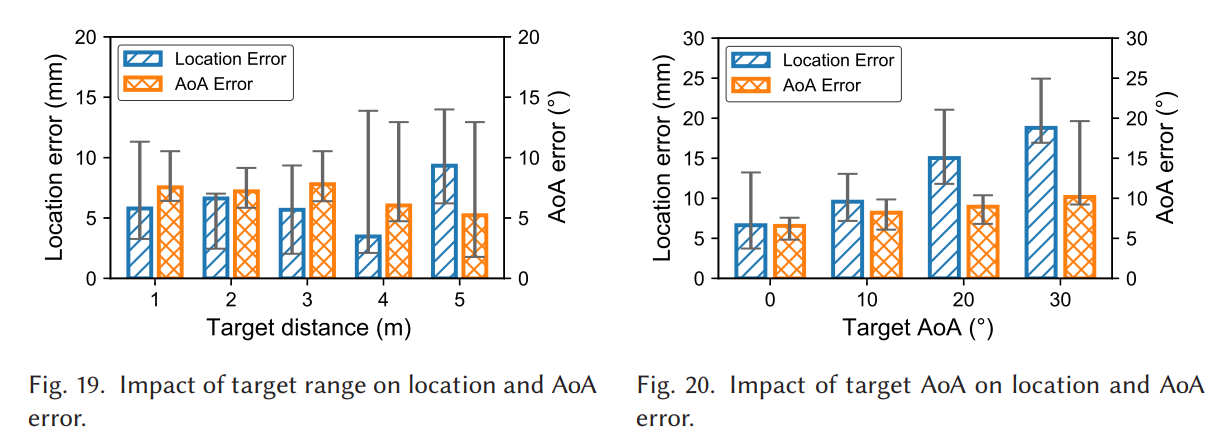
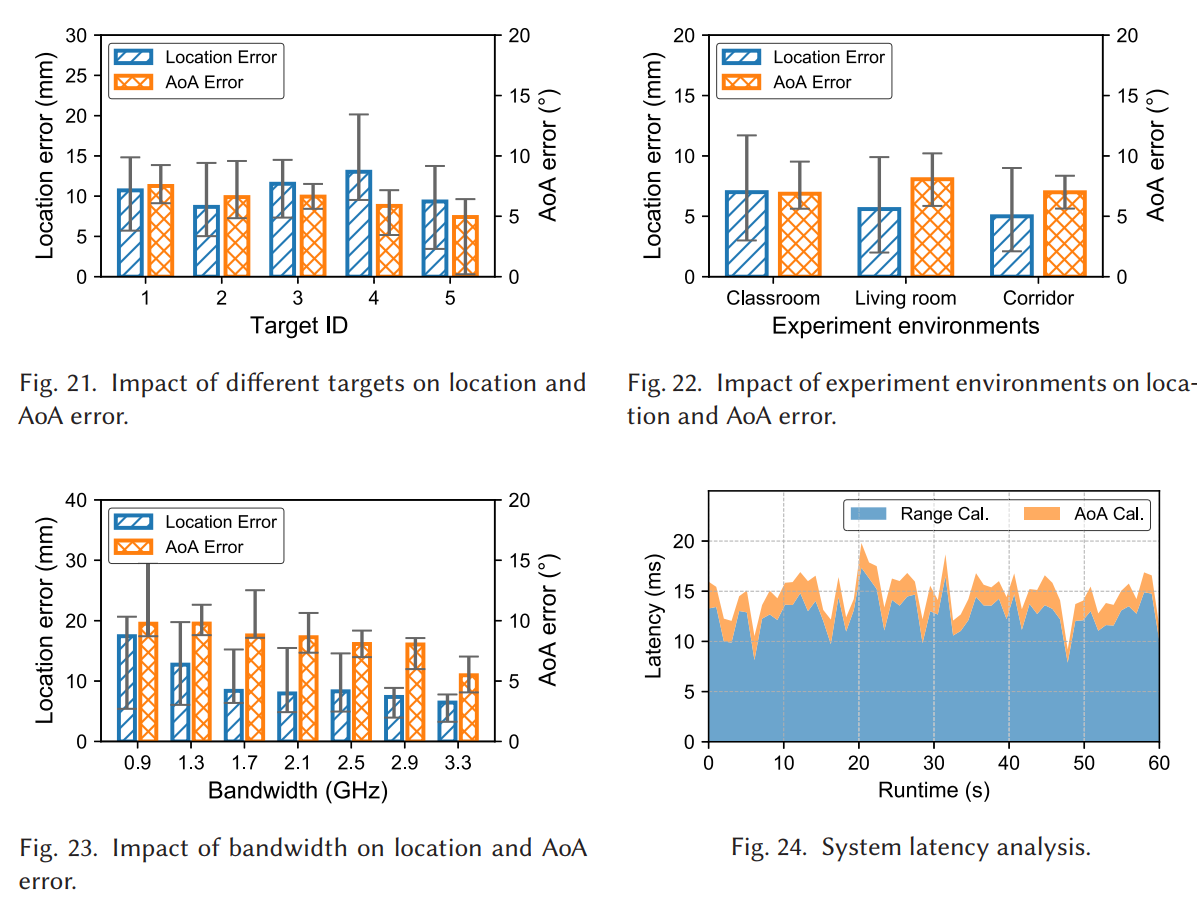
Fig.21--Fig.24 给出不同目标、不同环境、不同带宽、系统延迟。带宽下降会显著恶化误差:当带宽降到 0.9 GHz 时,中位定位误差与 AoA 误差约 17.4 mm 与 9.4°。系统端到端平均延迟 14.6 ms,其中距离计算(主要是优化)13.1 ms,AoA 1.5 ms,满足 50 Hz 实时输出。
10. 把整篇论文压缩为一句话:有限长复指数的 DFT 样本拟合
只用一句话概括 milliLoc 的数学本质:
对有限长观测下的复指数,DFT 采样点满足一个严格的解析形式(式(7) 的分式),它由 δ\deltaδ 与复幅度共同决定;milliLoc 用少量峰附近采样点对这一解析模型做加权非线性最小二乘拟合,同时估计 δ\deltaδ 与 A0ejθ0A_0e^{j\theta_0}A0ejθ0。于是距离从 kpk_pkp 变成 kp+δk_p+\deltakp+δ,AoA 从"峰点相位"变成"拟合初相 θ0\theta_0θ0"。
这也解释了它的边界:多目标频率过近时,多个 Dirichlet 形状高度重叠,拟合变病态;AoA 很大导致接收信号衰减,也会让拟合不稳。
附录:论文中省略/跳步的推导补全
附录 A:从发射 chirp 到 IF 式(3) 的完整推导
从式(1) 定义发射相位:
ϕTx(t)=2πf0t+πBTct2⇒STx(t)=cos(ϕTx(t)) \phi_{Tx}(t)=2\pi f_0 t+\frac{\pi B}{T_c}t^2 \quad\Rightarrow\quad S_{Tx}(t)=\cos(\phi_{Tx}(t)) ϕTx(t)=2πf0t+TcπBt2⇒STx(t)=cos(ϕTx(t))
接收信号是延迟 τ=2dc\tau=\frac{2d}{c}τ=c2d 且衰减的版本:
SRx(t)=αcos(ϕTx(t−τ)) S_{Rx}(t)=\alpha\cos(\phi_{Tx}(t-\tau)) SRx(t)=αcos(ϕTx(t−τ))
混频(相乘):
Smix(t)=STx(t) SRx(t)=αcos(ϕTx(t))cos(ϕTx(t−τ)) S_{mix}(t)=S_{Tx}(t)\,S_{Rx}(t) =\alpha\cos(\phi_{Tx}(t))\cos(\phi_{Tx}(t-\tau)) Smix(t)=STx(t)SRx(t)=αcos(ϕTx(t))cos(ϕTx(t−τ))
用恒等式 cosacosb=12[cos(a−b)+cos(a+b)]\cos a\cos b=\frac12[\cos(a-b)+\cos(a+b)]cosacosb=21[cos(a−b)+cos(a+b)]:
Smix(t)=α2cos(ϕTx(t)−ϕTx(t−τ))+α2cos(ϕTx(t)+ϕTx(t−τ)) S_{mix}(t) =\frac{\alpha}{2}\cos(\phi_{Tx}(t)-\phi_{Tx}(t-\tau)) +\frac{\alpha}{2}\cos(\phi_{Tx}(t)+\phi_{Tx}(t-\tau)) Smix(t)=2αcos(ϕTx(t)−ϕTx(t−τ))+2αcos(ϕTx(t)+ϕTx(t−τ))
低通滤波会滤掉高频的"和频项",保留差频项:
SIF(t)∝cos(Δϕ(t)),Δϕ(t)=ϕTx(t)−ϕTx(t−τ) S_{IF}(t)\propto \cos(\Delta\phi(t)) ,\quad \Delta\phi(t)=\phi_{Tx}(t)-\phi_{Tx}(t-\tau) SIF(t)∝cos(Δϕ(t)),Δϕ(t)=ϕTx(t)−ϕTx(t−τ)
把 ϕTx(t)\phi_{Tx}(t)ϕTx(t) 代入:
Δϕ(t)=2πf0(t−(t−τ))+πBTc(t2−(t−τ)2)=2πf0τ+πBTc(2tτ−τ2)=(2πf0τ−πBTcτ2)⏟ϕ0 (常数相位)+2πBTcτ⏟2πfb t \begin{aligned} \Delta\phi(t) &=2\pi f_0(t-(t-\tau))+\frac{\pi B}{T_c}\left(t^2-(t-\tau)^2\right)\\ &=2\pi f_0\tau+\frac{\pi B}{T_c}\left(2t\tau-\tau^2\right)\\ &=\underbrace{\left(2\pi f_0\tau-\frac{\pi B}{T_c}\tau^2\right)}{\phi_0\ \text{(常数相位)}} +\underbrace{\frac{2\pi B}{T_c}\tau}{2\pi f_b}\,t \end{aligned} Δϕ(t)=2πf0(t−(t−τ))+TcπB(t2−(t−τ)2)=2πf0τ+TcπB(2tτ−τ2)=ϕ0 (常数相位) (2πf0τ−TcπBτ2)+2πfb Tc2πBτt
因此拍频
fb=BTcτ=BTc⋅2dc=2BdcTc f_b=\frac{B}{T_c}\tau=\frac{B}{T_c}\cdot\frac{2d}{c}=\frac{2Bd}{cT_c} fb=TcBτ=TcB⋅c2d=cTc2Bd
于是
SIF(t)=α^cos (2πfbt+ϕ0)=α^cos (4πBdcTct+ϕ0) S_{IF}(t)=\hat{\alpha}\cos\!\left(2\pi f_b t+\phi_0\right) =\hat{\alpha}\cos\!\left(\frac{4\pi Bd}{cT_c}t+\phi_0\right) SIF(t)=α^cos(2πfbt+ϕ0)=α^cos(cTc4πBdt+ϕ0)
这就得到式(3)。
附录 B:距离分辨率式(4) 的"从 DFT 到距离"推导细化
对长度为 TcT_cTc 的连续观测窗,频率分辨率通常取 Δf=1Tc\Delta f=\frac{1}{T_c}Δf=Tc1。离散采样时若取 NNN 点、采样率 FsF_sFs,DFT bin 间隔为 FsN\frac{F_s}{N}NFs,而总观测时长近似 Tc≈NFsT_c\approx \frac{N}{F_s}Tc≈FsN,因此两种写法是一致的:
Δf=FsN≈1Tc \Delta f=\frac{F_s}{N}\approx \frac{1}{T_c} Δf=NFs≈Tc1
距离与拍频的比例关系为
fb=2BcTcd⇒∂fb∂d=2BcTc f_b=\frac{2B}{cT_c}d \quad\Rightarrow\quad \frac{\partial f_b}{\partial d}=\frac{2B}{cT_c} fb=cTc2Bd⇒∂d∂fb=cTc2B
于是一个频率 bin 的宽度对应的距离宽度
Δd=Δf∂fb/∂d=1Tc2BcTc=c2B \Delta d=\frac{\Delta f}{\partial f_b/\partial d} =\frac{\frac{1}{T_c}}{\frac{2B}{cT_c}} =\frac{c}{2B} Δd=∂fb/∂dΔf=cTc2BTc1=2Bc
这就是式(4)。
附录 C:式(7) 的逐行推导(几何级数 → 分式)
从式(5)(6) 出发,先忽略噪声项 w[n]w[n]w[n](保留它只会多出 W[k]W[k]W[k]):
R[k]=∑n=0N−1A0ejθ0ej2πfn e−j2πNnk=A0ejθ0∑n=0N−1ej2π(f−kN)n \begin{aligned} R[k] &=\sum_{n=0}^{N-1}A_0e^{j\theta_0}e^{j2\pi fn}\,e^{-j\frac{2\pi}{N}nk}\\ &=A_0e^{j\theta_0}\sum_{n=0}^{N-1}e^{j2\pi\left(f-\frac{k}{N}\right)n} \end{aligned} R[k]=n=0∑N−1A0ejθ0ej2πfne−jN2πnk=A0ejθ0n=0∑N−1ej2π(f−Nk)n
令 f=kp+δNf=\frac{k_p+\delta}{N}f=Nkp+δ,得
f−kN=kp+δ−kN f-\frac{k}{N}=\frac{k_p+\delta-k}{N} f−Nk=Nkp+δ−k
于是
R[k]=A0ejθ0∑n=0N−1ej2πN(kp+δ−k)n R[k]=A_0e^{j\theta_0}\sum_{n=0}^{N-1}e^{j\frac{2\pi}{N}(k_p+\delta-k)n} R[k]=A0ejθ0n=0∑N−1ejN2π(kp+δ−k)n
令 k=kp−mk=k_p-mk=kp−m,则 kp+δ−k=δ+mk_p+\delta-k=\delta+mkp+δ−k=δ+m:
R[kp−m]=A0ejθ0∑n=0N−1ej2πN(δ+m)n R[k_p-m]=A_0e^{j\theta_0}\sum_{n=0}^{N-1}e^{j\frac{2\pi}{N}(\delta+m)n} R[kp−m]=A0ejθ0n=0∑N−1ejN2π(δ+m)n
这是一段几何级数。设
ρ=ej2πN(δ+m) \rho=e^{j\frac{2\pi}{N}(\delta+m)} ρ=ejN2π(δ+m)
则
∑n=0N−1ρn=1−ρN1−ρ=1−ej2π(δ+m)1−ej2πN(δ+m) \sum_{n=0}^{N-1}\rho^n=\frac{1-\rho^N}{1-\rho} =\frac{1-e^{j2\pi(\delta+m)}}{1-e^{j\frac{2\pi}{N}(\delta+m)}} n=0∑N−1ρn=1−ρ1−ρN=1−ejN2π(δ+m)1−ej2π(δ+m)
因此
R[kp−m]=A0ejθ01−ej2π(δ+m)1−ej2πN(δ+m) R[k_p-m]=A_0e^{j\theta_0} \frac{1-e^{j2\pi(\delta+m)}}{1-e^{j\frac{2\pi}{N}(\delta+m)}} R[kp−m]=A0ejθ01−ejN2π(δ+m)1−ej2π(δ+m)
加入噪声的 DFT 项 W[kp−m]W[k_p-m]W[kp−m] 就是式(7)。
附录 D:把式(7) 化成"幅度项 × 相位项",直观看清 δ\deltaδ 如何扭曲相位
用恒等式
1−ej2πx=−2jejπxsin(πx) 1-e^{j2\pi x}=-2je^{j\pi x}\sin(\pi x) 1−ej2πx=−2jejπxsin(πx)
对分子分母分别处理,令 x=δ+mx=\delta+mx=δ+m:
1−ej2πx1−ej2πNx=−2jejπxsin(πx)−2jejπNxsin(πNx)=ejπx(1−1N)⋅sin(πx)sin(πNx) \frac{1-e^{j2\pi x}}{1-e^{j\frac{2\pi}{N}x}} =\frac{-2je^{j\pi x}\sin(\pi x)}{-2je^{j\frac{\pi}{N}x}\sin\left(\frac{\pi}{N}x\right)} =e^{j\pi x\left(1-\frac1N\right)} \cdot \frac{\sin(\pi x)}{\sin\left(\frac{\pi}{N}x\right)} 1−ejN2πx1−ej2πx=−2jejNπxsin(Nπx)−2jejπxsin(πx)=ejπx(1−N1)⋅sin(Nπx)sin(πx)
于是
R[kp−m]≈A0[sin(π(δ+m))sin(πN(δ+m))]⋅ej(θ0+π(δ+m)(1−1N)) R[k_p-m] \approx A_0 \left[ \frac{\sin(\pi(\delta+m))}{\sin\left(\frac{\pi}{N}(\delta+m)\right)} \right] \cdot e^{j\left(\theta_0+\pi(\delta+m)\left(1-\frac1N\right)\right)} R[kp−m]≈A0[sin(Nπ(δ+m))sin(π(δ+m))]⋅ej(θ0+π(δ+m)(1−N1))
这一写法很有启发性:
前面的正弦比值决定幅度形状(峰的泄漏形状),后面的指数决定相位随 δ\deltaδ 的系统漂移。AoA 的问题正是从这类系统漂移里长出来的。
附录 E:式(15) 为什么必然出现,以及 F(δ)F(\delta)F(δ) 的相位到底是什么
取式(7) 的 m=0m=0m=0(也就是 k=kpk=k_pk=kp):
R[kp]=A0ejθ01−ej2πδ1−ej2πNδ+W[kp] R[k_p]=A_0e^{j\theta_0}\frac{1-e^{j2\pi\delta}}{1-e^{j\frac{2\pi}{N}\delta}}+W[k_p] R[kp]=A0ejθ01−ejN2πδ1−ej2πδ+W[kp]
忽略噪声,定义
F(δ)=1−ej2πδ1−ej2πNδ F(\delta)=\frac{1-e^{j2\pi\delta}}{1-e^{j\frac{2\pi}{N}\delta}} F(δ)=1−ejN2πδ1−ej2πδ
则
R[kp]≈A0ejθ0F(δ)⇒∠R[kp]=θ0+∠F(δ) R[k_p]\approx A_0e^{j\theta_0}F(\delta) \quad\Rightarrow\quad \angle R[k_p]=\theta_0+\angle F(\delta) R[kp]≈A0ejθ0F(δ)⇒∠R[kp]=θ0+∠F(δ)
这就是式(15) 的来源。
进一步,用附录 D 的处理(令 x=δx=\deltax=δ):
F(δ)=ejπδ(1−1N)⋅sin(πδ)sin(πNδ) F(\delta) =e^{j\pi\delta\left(1-\frac1N\right)} \cdot \frac{\sin(\pi\delta)}{\sin\left(\frac{\pi}{N}\delta\right)} F(δ)=ejπδ(1−N1)⋅sin(Nπδ)sin(πδ)
注意到当 δ∈(−12,12)\delta\in(-\tfrac12,\tfrac12)δ∈(−21,21) 时,sin(πδ)\sin(\pi\delta)sin(πδ) 与 sin(πNδ)\sin(\frac{\pi}{N}\delta)sin(Nπδ) 同号,因此正弦比值为正实数(相位为 0)。于是
∠F(δ)=πδ(1−1N)(δ∈(−12,12)) \angle F(\delta)=\pi\delta\left(1-\frac1N\right)\quad(\delta\in(-\tfrac12,\tfrac12)) ∠F(δ)=πδ(1−N1)(δ∈(−21,21))
这给出一个非常具体的结论:峰点相位相对初相的系统偏差大约是 πδ(1−1N)\pi\delta(1-\frac1N)πδ(1−N1),在 NNN 很大时近似 πδ\pi\deltaπδ。
这也解释了为什么仅仅"增大 FFT 点数/零填充"并不能从根上解决:零填充只增加采样密度,并不会改变真实 δ\deltaδ 造成的相位结构;而 milliLoc 是直接把 δ\deltaδ 拟合出来,再用 θ0\theta_0θ0 绕开 ∠F(δ)\angle F(\delta)∠F(δ)。
附录 F:式(11) 的推导细化(从 DFT bin 到拍频,再到距离)
DFT 的 kkk bin 对应的实际频率近似为
fk=kNFs f_k=\frac{k}{N}F_s fk=NkFs
真实拍频是
fb=kp+δNFs f_b=\frac{k_p+\delta}{N}F_s fb=Nkp+δFs
而 FMCW 的距离-拍频关系是
fb=2BcTcd⇒d=cTc2Bfb f_b=\frac{2B}{cT_c}d \quad\Rightarrow\quad d=\frac{cT_c}{2B}f_b fb=cTc2Bd⇒d=2BcTcfb
代入 fbf_bfb:
d=cTc2B⋅kp+δNFs=kp+δN⋅cFsTc2B d=\frac{cT_c}{2B}\cdot\frac{k_p+\delta}{N}F_s =\frac{k_p+\delta}{N}\cdot\frac{cF_sT_c}{2B} d=2BcTc⋅Nkp+δFs=Nkp+δ⋅2BcFsTc
这就是式(11)。
附录 G:多目标时"需要多少个 DFT 采样点"的计数推导
对 uuu 个频率分量,每个分量需要估计三个实参数:幅值 AiA_iAi、初相 θi\theta_iθi、偏移 δi\delta_iδi,总未知实参数数目为 3u3u3u。
每一个 DFT 采样点 R[k]R[k]R[k] 是复数,等价提供两条独立实方程(实部与虚部)。因此若选用 MMM 个 DFT 采样点,总实方程数约为 2M2M2M。要使方程数不少于未知量,至少需要
2M≥3u⇒M≥⌈3u2⌉ 2M\ge 3u \quad\Rightarrow\quad M\ge \left\lceil\frac{3u}{2}\right\rceil 2M≥3u⇒M≥⌈23u⌉
这正是论文里"需要 ⌈32u⌉\lceil \frac{3}{2}u\rceil⌈23u⌉ 个 DFT 样本"的来源。
附录 H:幅度加权(AM)在优化里等价于一个加权最小二乘
把式(10) 写成更标准的形式会更清楚。设参数向量
β=[A0,θ0,δ]T \boldsymbol{\beta}=[A_0,\theta_0,\delta]^T β=[A0,θ0,δ]T
对每个选中的频点 kik_iki,定义模型预测
R^[ki;β]=A0ejθ01−ej2π(δ+kp−ki)1−ej2πN(δ+kp−ki) \hat R[k_i;\boldsymbol{\beta}] =A_0e^{j\theta_0} \frac{1-e^{j2\pi(\delta+k_p-k_i)}}{1-e^{j\frac{2\pi}{N}(\delta+k_p-k_i)}} R^[ki;β]=A0ejθ01−ejN2π(δ+kp−ki)1−ej2π(δ+kp−ki)
复残差
ei(β)=R[ki]−R^[ki;β] e_i(\boldsymbol{\beta})=R[k_i]-\hat R[k_i;\boldsymbol{\beta}] ei(β)=R[ki]−R^[ki;β]
把复残差展开成实向量(把实部与虚部堆叠),得到残差向量 e(β)∈R2M\mathbf{e}(\boldsymbol{\beta})\in\mathbb{R}^{2M}e(β)∈R2M。AM 相当于给每个频点一个权重 wi=∣R[ki]∣w_i=|R[k_i]|wi=∣R[ki]∣,于是目标函数就是
minβ∑i=1Mwi2 ∥ei(β)∥22⇔minβ∥We(β)∥22 \min_{\boldsymbol{\beta}} \sum_{i=1}^{M} w_i^2 \,\|e_i(\boldsymbol{\beta})\|2^2 \quad\Leftrightarrow\quad \min{\boldsymbol{\beta}}\|\mathbf{W}\mathbf{e}(\boldsymbol{\beta})\|_2^2 βmini=1∑Mwi2∥ei(β)∥22⇔βmin∥We(β)∥22
其中 W=diag(w1,w1,w2,w2,...,wM,wM)\mathbf{W}=\mathrm{diag}(w_1,w_1,w_2,w_2,\dots,w_M,w_M)W=diag(w1,w1,w2,w2,...,wM,wM)(每个复残差拆成两维,所以权重要重复两次)。
LM 的更新在这种加权形式下写作
(JTWTWJ+λI)Δβ=JTWTWe(\mathbf{J}^T\mathbf{W}^T\mathbf{W}\mathbf{J}+\lambda\mathbf{I})\Delta\boldsymbol{\beta} =\mathbf{J}^T\mathbf{W}^T\mathbf{W}\mathbf{e} (JTWTWJ+λI)Δβ=JTWTWe
J\mathbf{J}J 是残差对参数的雅可比矩阵,λ\lambdaλ 是阻尼项。如果要复现算法,真正的工程关键其实是:如何选 kik_iki(论文经验最优为 3 个、尽量靠近峰点),以及如何初始化 δ\deltaδ(通常可从峰点附近幅度不对称性给一个粗值),这样 LM 才不容易陷入局部不良点。
附录 I:峰点法在 4 cm bin 下"理论中位误差约 1 cm"的推导
假设峰点法输出的是 bin 中心或某个固定代表值,而真实目标在 bin 内均匀分布。若 bin 宽为 W=4W=4W=4 cm,则真实位置相对输出的误差幅值 ∣E∣|E|∣E∣ 可近似服从 [0,W/2][0, W/2][0,W/2] 上的均匀分布(因为最大偏差是半个 bin)。
均匀分布 U(0,a)U(0,a)U(0,a) 的中位数是 a/2a/2a/2。这里 a=W/2=2a=W/2=2a=W/2=2 cm,因此误差中位数为
median(∣E∣)=a2=W4=1 cm \mathrm{median}(|E|)=\frac{a}{2}=\frac{W}{4}=1\text{ cm} median(∣E∣)=2a=4W=1 cm
这就是论文正文里对 peak-pt 中位误差量级的解释来源,也很好地说明了为什么要把 δ\deltaδ 拟合出来:它相当于在一个 bin 内恢复连续位置,从而把"必然存在的 0--2 cm 量化误差"压到毫米级。