文章目录
前言
快速排序是一种基于交换的排序算法,通过分治策略将待排序序列划分为两部分。算法首先选取基准元素(通常为首元素),使用双指针low和high从序列两端向中间扫描,确保low指针左侧元素均小于基准,high指针右侧元素均大于等于基准。通过不断交换元素位置,最终将基准元素放置到正确位置,完成一次划分。然后递归地对左右子序列重复上述过程,直至所有元素有序。示例中展示了以49为基准的一次完整划分过程,通过双指针交替移动和元素交换实现排序。该算法平均时间复杂度为O(nlogn),是一种高效的排序方法。
基于"交换"的排序:根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置
一.思想
- 算法思想:在待排序表 L [ 1... n ] L[1 ... n] L[1...n]中任取一个元素 pivot \text{pivot} pivot作为枢轴(或基准,通常取首元素),通过一趟排序将待排序表划分为独立的两部分 L [ 1... k − 1 ] L[1 ... k-1] L[1...k−1]和 L [ k + 1... n ] L[k+1 ... n] L[k+1...n],使得 L [ 1... k − 1 ] L[1 ... k-1] L[1...k−1]中的所有元素小于 pivot, L [ k + 1... n ] \text{pivot},L[k+1 ... n] pivot,L[k+1...n]中的所有元素大于等于 pivot \text{pivot} pivot,则 pivot \text{pivot} pivot放在了其最终位置L(k)上,这个过程称为一次"划分"。然后分别递归地对两个子表重复上述过程,直至每部分内只有一个元素或空为止,即所有元素放在了其最终位置上。
二.具体例子
- 增序

- 我们用low和high两个指针分别指向此时我们要处理的这个序列的头和尾两个位置
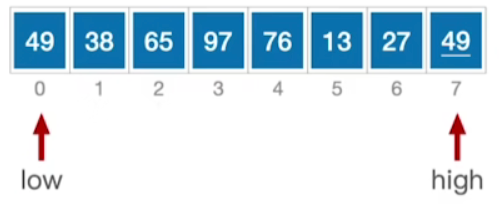
- 然后我们选择low所指向的这个元素让它作为所谓的基准元素(枢轴元素)
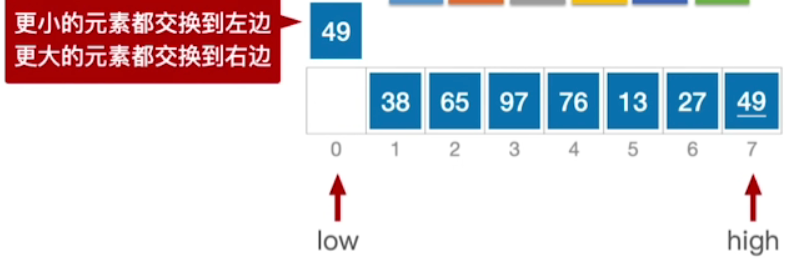
- 接下来我们会让low和high这两个指针开始往中间移动,把所有的这些带排序的元素都给扫描一遍,在整个扫描的过程当中,我们需要保证high所指的这个指针的右边都是大于等于当前的基准元素49,而low指针它的左边,我们要保证都是小于49的元素
- 由于此时low所指的这个位置是空的,所以我们先让high向左移动,那high当前所指的元素49 ≥ 49,所以下标为7的这个元素并不需要移动,然后high--
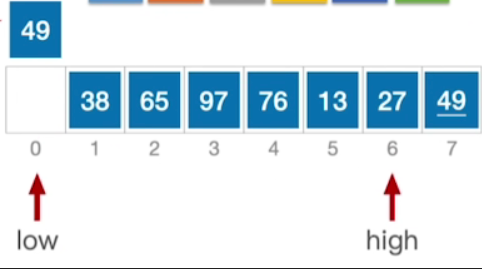
- 此时high所指的这个元素是要小于49的,由于所有小于49的元素都应该放到low指针它所指的位置的左边,所以我们可以把27这个元素,让它移动到low所指的这个位置
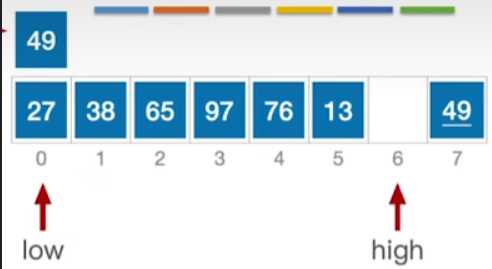
- 现在high所指的这个位置空出来了,那接下来我们让low指针往右移动,此时low所指的位置是要小于49的,所以不需要把它移到右边,接下来让low指针右移
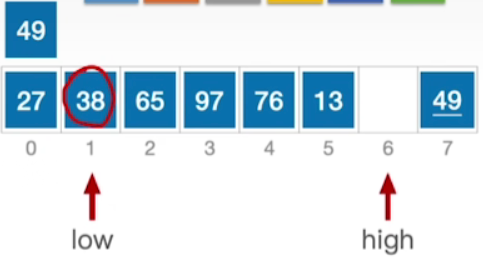
- 当前low指向的这个元素同样小于49,不需要把它移到右边,接下来让low指针右移
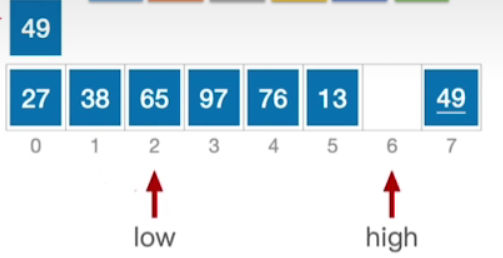
- 当前low指向的这个元素已经大于了49,因此将其移动到high所指的位置
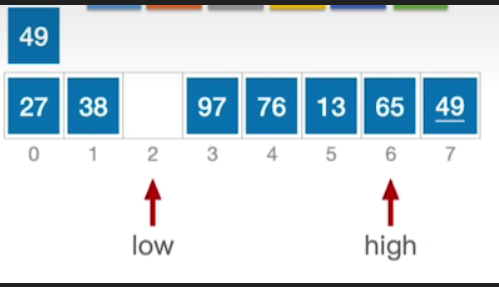
- 接下来low所指的这个位置空了,因此我们看high指针,此时 high所指的元素是要大于等于49的,所以不需要移动,因此让high指针左移
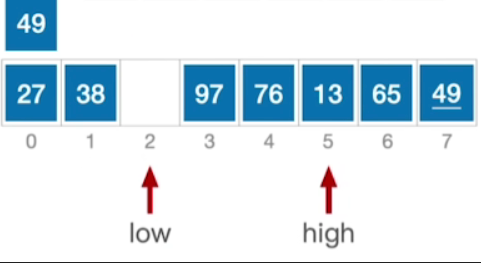
- 当前high所指的元素小于49,因此将49移动到low指向的位置
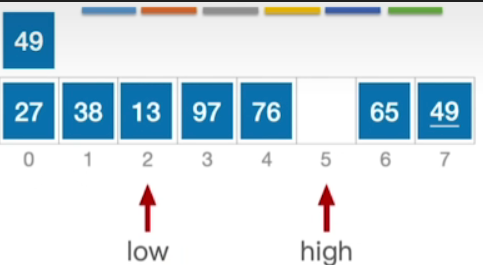
- 由于high指向空,因此接下来切换回low指针,13<49,因此low指针右移
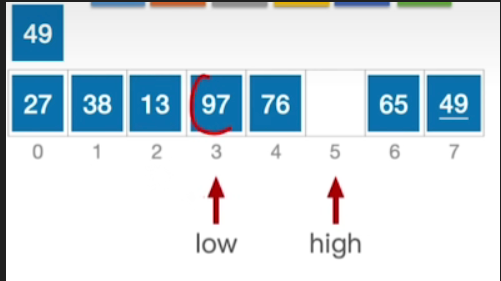
- 此时low所指元素为97>49,因此需要将97右移到high所指向的位置
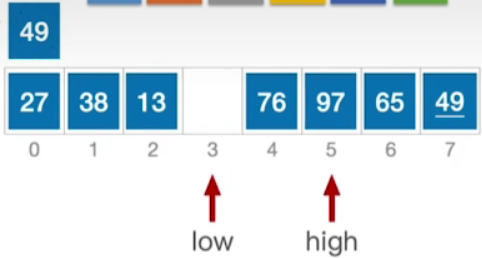
- 现在又切换回high指针,97>49,因此直接将high左移即可
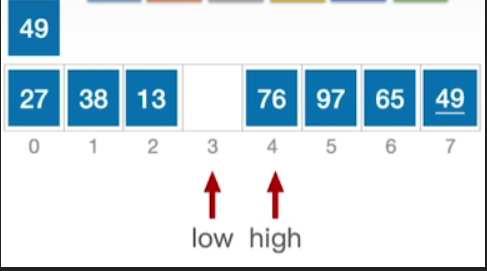
- 此时high指向元素为76≥49,所以high--
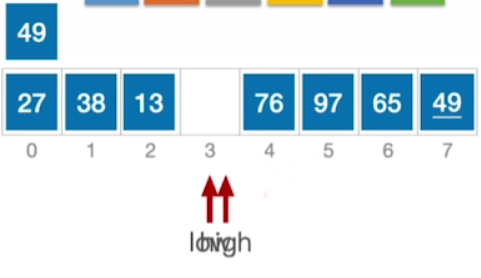
- 当low和high碰到一起的时候,就说明其实我们已经把所有的这些带排序的元素,都给扫了一遍,所有比基准元素49更小的元素,都把它放到了low指针所指位置的左边,而所有比49这个基准元素更大的或者相等的元素,我们统统把它放在了high指针所指的右半部分,因此49一定放在low和high相遇的这个位置

- 此时49这个元素的最终位置已确定
- 由于此时low所指的这个位置是空的,所以我们先让high向左移动,那high当前所指的元素49 ≥ 49,所以下标为7的这个元素并不需要移动,然后high--
- 对已经确定位置的元素49的左右这两个子表,再一次的用同样的方法进行划分
- 左子表,依旧用low和high分别指向表的首元素和尾元素
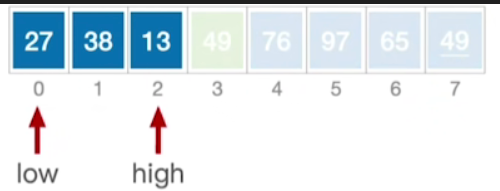
- 选中最前边的一个元素27作为基准元素,后面也是和之前一样的步骤
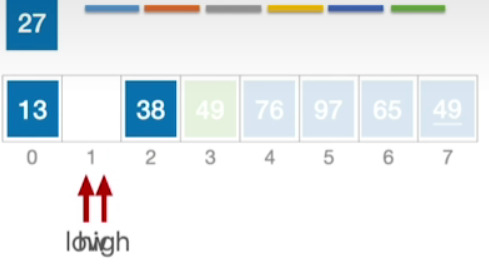
- low和high相遇的位置就是基准元素27的插入位置
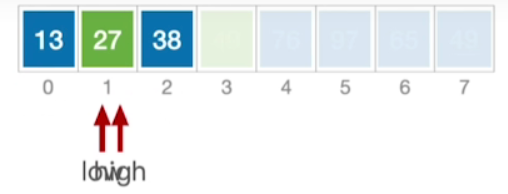
- 接下来0~2这个子表又再一次的被我们刚才选中的数轴元素,划分为了左右两个部分,那由于我们剩余的左右两个部分都只有一个元素,所以显然这两个部分我们不需要再进行别的处理
- 也就是说0~2这个子表当中,所有这些元素的最终位置,我们此时都已经确定了
- 右子表,和之前一样的操作,不做赘述
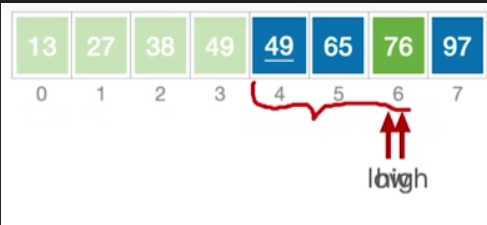
- 对于4~7这个子表,通过基准元素76,再次的把它划分成了更小的两个部分,对于左半部分的处理思路是一样的,不做赘述
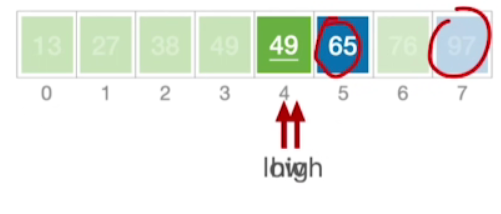
- 显然,65和97这两个元素的最终位置也被确定了

- 左子表,依旧用low和high分别指向表的首元素和尾元素
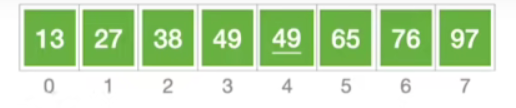
- 这就是最终结果
三.代码实现
1.具体代码
c
//用第一个元素将待排序序列分成左右两个部分
int Partition(int A[],int low,int high){
int pivot=A[low]; //第一个元素作为枢轴
while(low<high&&A[high]>=pivot)--high;
A[low]=A[high]; //比枢轴小的元素移动到左端
while(low<high&&A[low]<=pivot)++low;
A[high]=A[low]; //比枢轴大的元素移动到右端
}
A[[low]=pivot;//枢轴元素存放到最终位置
return low;
}
c
93 //快速排序
94 void QuickSort(int A[], int low, int high){
95 if(low & high){//递归跳出的条件
96 int pivotpos= partition(A, low, high); //划分
97 QuickSort(A, low, pivotpos-1); //划分左子表
98 QuickSort(A, pivotpos+1, high); //划分右子表
99 }
100}2.代码运行过程
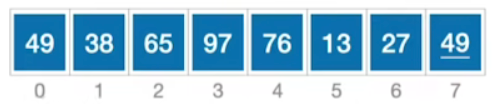
- 刚开始会传入整个数组a的值,同时指明最左边的元素和最右边的元素,下标应该是0~7这个范围
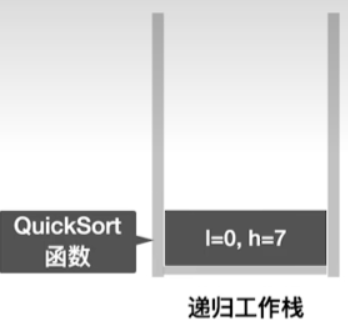
- 此时满足if条件low小于high,因此进入if条件进行处理
if(low< high),接下来会调用Partition这个函数int pivotpos= partition(A, low, high);,这个函数的功能就是进行一次划分,我们要把a这个数组的low到high内的元素进行一个划分,所以接下来在函数调用栈当中会压入和Partition这个函数相关的一些的信息,同时记录QuickSort函数执行到了第几行,此时是执行到了96行(#96)
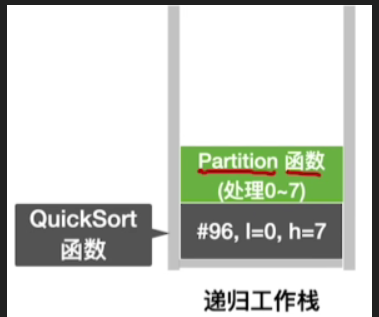
- 此时我们传入的low = 0和high = 7值给Partition函数,此时用临时变量pivot(基准/枢轴)存放low指针所指向的这个元素作为基准
int pivot=A[Low];
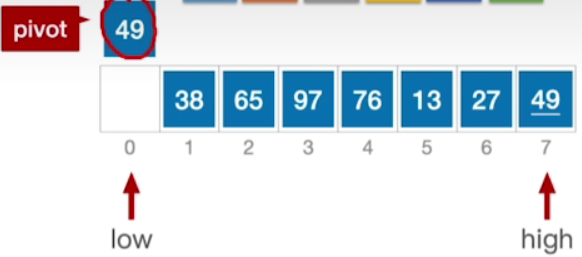
- 此时外层while循环判断low < high
while(low<high)- 因此进入第一个内层while循环,第一个内层while循环会判断low是否小于high且此时high指向的元素是否大于等于基准,如果是,则直接左移high
- 很显然,这层while循环做的事情是让high指针不断地左移,直到找到一个比枢轴元素更小的元素为止
while(low<high&&A[high]>==pivot)--high;
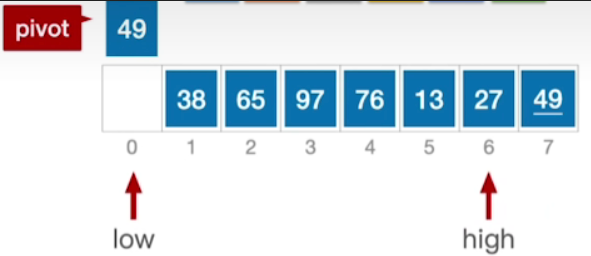
- 很显然,这层while循环做的事情是让high指针不断地左移,直到找到一个比枢轴元素更小的元素为止
- 此时发现high所指元素比pivot更小,因此将high所指元素覆盖到low所指元素
A[low]=A[high];
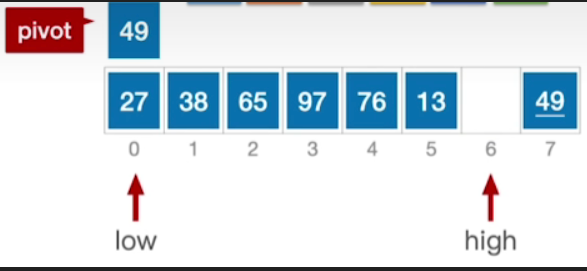
- 接下来就是进入第二个内层循环,第二个内层while循环会判断low是否小于high且此时low指向的元素是否小于基准,如果是,则直接右移low
- 很显然,这层while循环做的事情是让low指针不断地右移,直到找到一个比枢轴元素更大的元素为止
while(low<high&&A[low]<=pivot)++low;
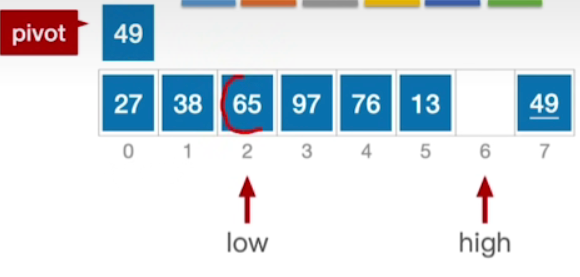
- 很显然,这层while循环做的事情是让low指针不断地右移,直到找到一个比枢轴元素更大的元素为止
- 此时发现low所指元素比pivot更大,因此将low所指元素覆盖到high所指元素
A[high]=A[low];
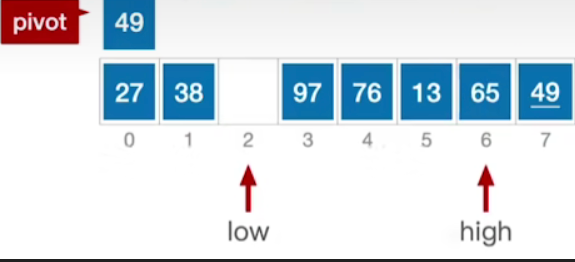
- 因此进入第一个内层while循环,第一个内层while循环会判断low是否小于high且此时high指向的元素是否大于等于基准,如果是,则直接左移high
- 此时发现low仍小于high,因此继续重复上面的操作,结果如下
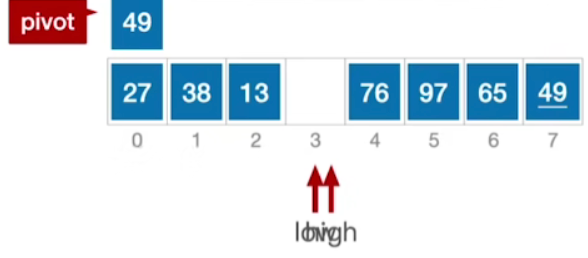
- 此时由于low = high,因此
A[high]=A[low];或者A[low]=A[high];不再起作用,并且可以跳出外层循环,将pivot的值复制到low和high一起指向的位置A[low]=pivot;

- 最终返回这个low的值作为新的边界分割原表,同时将第一层QuickSor函数pivotpos = 3,函数代码执行到97的信息更新到函数调用栈
int pivotpos=partition(A, low, high);
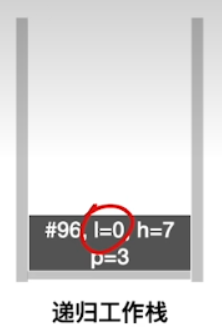
- 查看函数调用栈中之前是执行到了96行,因此此时我们需要执行第97行,划分左子表(low = 0 ~ pivotpos - 1 = 2)
QuickSort(A, low, pivotpos-1);,此时将low = 0,high等于2,的QuickSort函数信息压入栈中
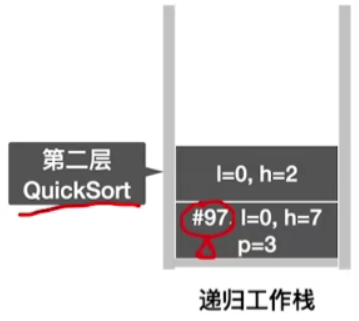
- 处理过程和之前的一层QuickSort函数处理一致,不多赘述
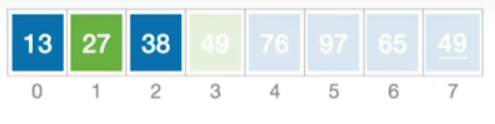
- 同时将第二层函数pivotpos = 1,函数代码执行到96的信息更新到函数调用栈
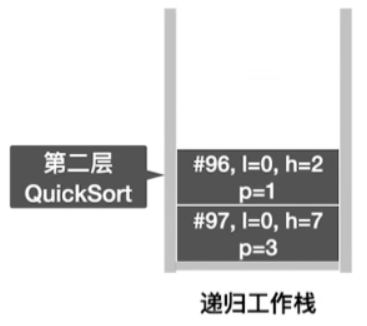
- 查看函数调用栈中最顶层函数的执行行数为96行,因此接下来执行97行,也就是划分左子表
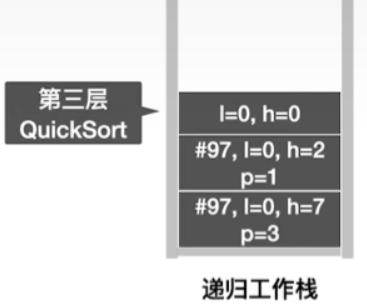
- 由于low等于high,说明此时这个子表当中其实只剩余一个元素,不满足if的条件
if(low<high),因此可以直接返回执行第二层QuickSort,通过查看这一层的信息得知之前是执行到了第97行,因此此时执行第98行,也就是划分右子表QuickSort(A,pivotpos+1,high);
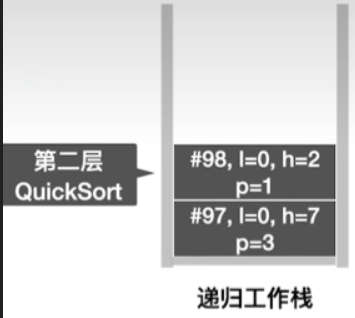
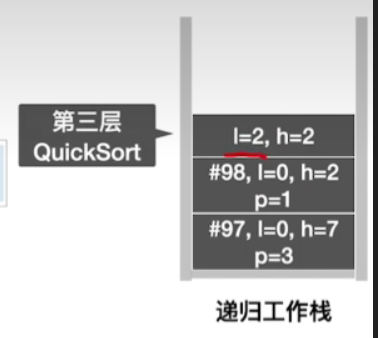
- 由于low = high,因此直接回到第二层,发现第二层执行到了第98行,后面已经没有可执行语句,因此返回第一层

- 此时发现第一层函数执行到了第97行,因此接下来执行第98行
QuickSort(A,pivotpos+1,high);
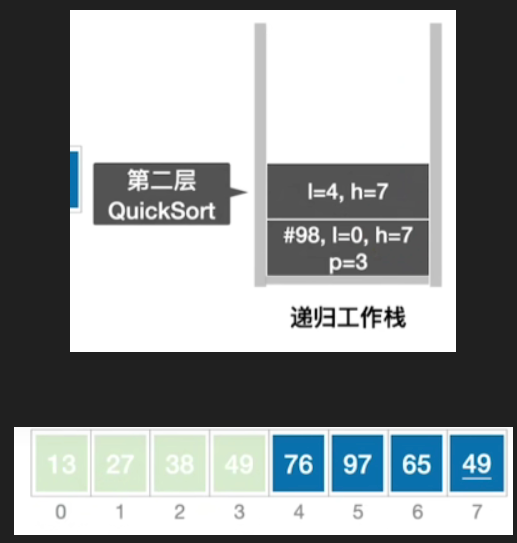
- 后面的步骤也差不多,因此不再赘述,图片过程如下

- 接着更新第二层函数的函数调用栈
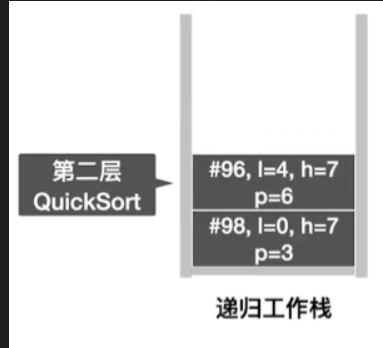
- 处理左子表
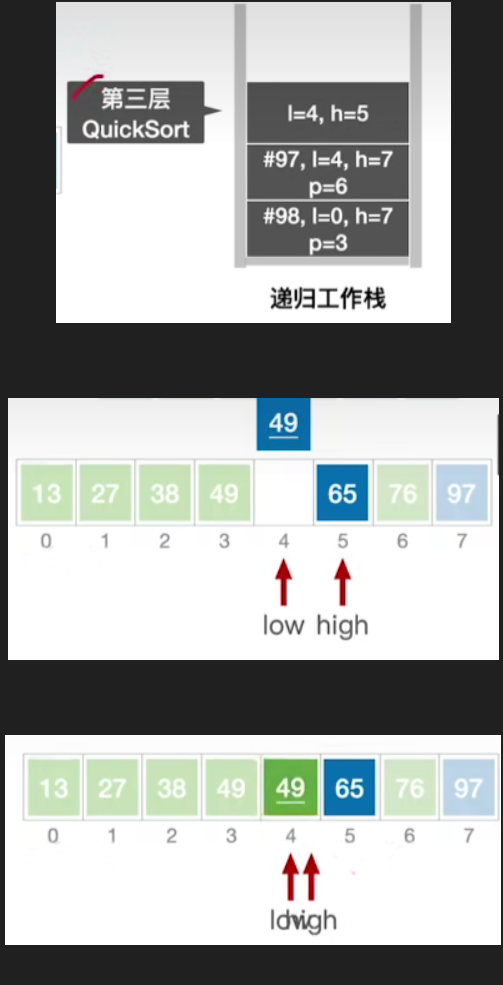
- 更新第三层函数的函数调用栈
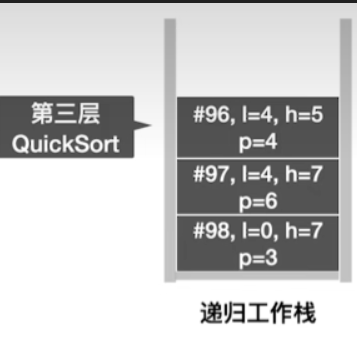
- 接下来不再赘述,结果如下
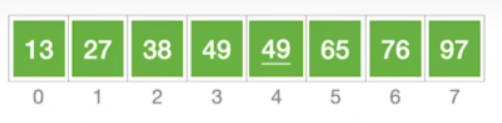
四.算法效率分析
1.时间复杂度
1.基本分析
- 初始序列:由于Partition函数是两个指针不断往中间移动,因此其时间复杂度不会超过O(n)

- 第一层QuickSort处理后:由于Partition函数是两个指针不断往中间移动,因此其时间复杂度不会超过O(n)

- 第二层QuickSort处理后:同样不会超过O(n)

- 第三层QuickSort处理后:同样不会超过O(n)

- 第四层QuickSort处理后,得到最终序列

- 可以看出:每一层的QuickSort只需要处理剩余的待排序元素,时间复杂度不超过O(n)
- 因此: 时间复杂度 = O ( n ∗ 递归层数 ) 时间复杂度=O(n*递归层数) 时间复杂度=O(n∗递归层数)
2.进一步分析
- 递归可以画成如下图进行表示
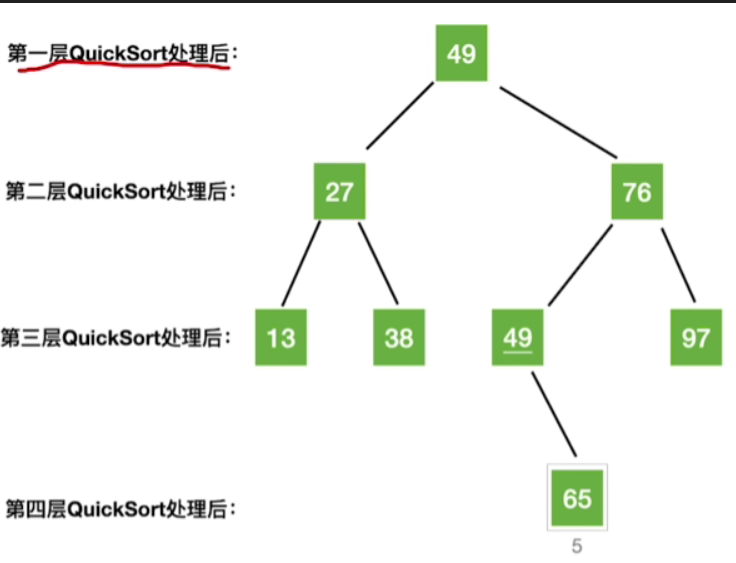
- 把n个元素组织成二叉树,二叉树的层数就是递归调用的层数
- 由于n 个结点的二叉树
最小高度 = ⌊ log 2 n ⌋ + 1 最小高度 = \lfloor\log_{2}n\rfloor +1 最小高度=⌊log2n⌋+1
最大高度 = n 最大高度 = n 最大高度=n - 因此:
最好时间复杂度 = O ( n ∗ ⌊ log 2 n ⌋ + 1 ) → O ( n l o g 2 n ) 最好时间复杂度=O(n*\lfloor\log_{2}n\rfloor +1)\rightarrow O(nlog_2n) 最好时间复杂度=O(n∗⌊log2n⌋+1)→O(nlog2n)
最坏时间复杂度 : O ( n 2 ) 最坏时间复杂度:O(n^2) 最坏时间复杂度:O(n2)
3.总结
- 最好时间复杂度: O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
- 平均时间复杂度= O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
- 最坏时间复杂度: O ( n 2 ) O(n^2) O(n2)
快速排序是所有内部排序算法中平均性能最优的排序算法
2.空间复杂度
- 空间复杂度 = O ( 递归层数 ) 空间复杂度=O(递归层数) 空间复杂度=O(递归层数)
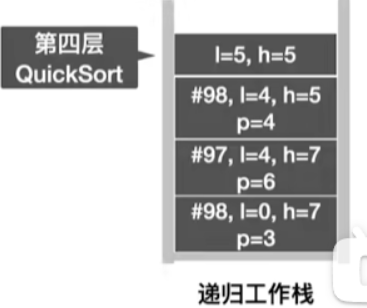
- 因此:
最好空间复杂度= O ( l o g 2 n ) O(log_2n) O(log2n)
最坏空间复杂度= O ( n ) O(n) O(n)
若每一次选中的"枢轴"将待排序序列划分为很不均匀的两个部分,则会导致递归深度增加,算法效率变低
若每一次选中的"枢轴"将待排序序列划分为均匀的两个部分,则递归深度最小,算法效率最高
总结:若初始序列有序或逆序,则快速排序的性能最差(因为每次选择的都是最靠边的元素)
3.稳定性
- 不稳定
- 例
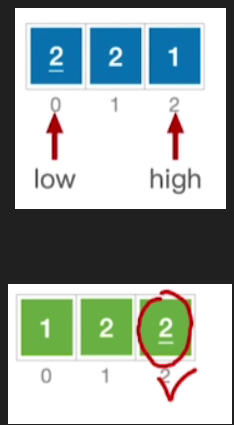
4.适用性
-
普通的快速排序可以应用于链表,但由于链表结构的特性,其性能优势不如在数组上明显
-
方法
- 选择基准:通常选择链表的头节点作为基准元素(pivot)。
- 划分分区:使用两个指针(例如
small和cur)。small指针指向已处理部分中所有小于基准的节点的最后一个。cur指针遍历链表。当cur指向的节点值小于基准值时,将small指针后移,然后交换small和cur节点的值。这样就能将小于基准的节点逐步归拢到链表前半部分。 - 基准归位:遍历完成后,将基准节点与
small指针所指节点交换值。此时,基准节点就位于正确位置,其左边节点的值都小于它,右边节点的值都大于等于它。 - 递归排序:递归地对基准左边和右边的两个子链表进行快速排序
五.快速排序的优化
1.思路
- 尽量选择可以把数据中分的枢轴元素。
eg:①选头、中、尾三个位置的元素,取中间值作为枢轴元素;②随机选一个元素作为枢轴元素
2.随机选取基准代码实现
c
// 交换函数
void Swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 快速排序辅助函数(划分左右子表)
int Partition(int arr[], int low, int high) {
// 优化:随机选择基准,避免最坏情况
int randomIndex = low + rand() % (high - low + 1);
Swap(&arr[low], &arr[randomIndex]); // 将随机基准交换到首位
int pivot = arr[low];
while (low < high) {
// 从右往左找到一个小于基准元素的数
while (low < high && arr[high] >= pivot) high--;
arr[low] = arr[high]; // 覆盖
// 从左往右找到一个大于基准元素的数
while (low < high && arr[low] <= pivot) low++; // 修正:low++
arr[high] = arr[low]; // 覆盖
}
arr[low] = pivot; // 基准归位
return low;
}
// 快速排序主函数
void QuickSort(int arr[], int low, int high) {
if (low < high) {
// 划分子表
int pivot = Partition(arr, low, high);
// 递归左子表
QuickSort(arr, low, pivot - 1);
// 递归右子表
QuickSort(arr, pivot + 1, high);
}
}
// 快速排序启动函数
void QuickSortStrart(int arr[], int length) {
int low = 0, high = length - 1;
// 将分别用low和high指向数组的首尾
QuickSort(arr, low, high);
}3.三数取中法代码实现
c
// 快速排序辅助函数(划分左右子表)
int Partition(int arr[], int low, int high) {
int pivot = arr[low];// 定下基准元素
while (low < high) {
// 从右往左找到一个小于基准元素的数
while (low < high && arr[high] >= pivot) high--;
// 找到后将arr[high]覆盖到arr[low]
arr[low] = arr[high];
// 从左往右找到一个大于基准元素的数
while (low < high && arr[low] <= pivot) low++;
// 找到后将arr[low]覆盖到arr[high]
arr[high] = arr[low];
}
// 将基准元素插入到最终位置
arr[low] = pivot;
// 返回基准元素的位置
return low;
}
// 交换两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 三数取中函数,返回中位数的索引
int medianOfThree(int arr[], int low, int high) {
// 计算中间位置的索引,避免直接相加可能导致的整数溢出
int mid = low + (high - low) / 2;
// 通过三次比较,对arr[low], arr[mid], arr[high]进行排序
// 目标:使得 arr[low] <= arr[mid] <= arr[high]
if (arr[mid] < arr[low]) {
swap(&arr[low], &arr[mid]);
}
if (arr[high] < arr[low]) {
swap(&arr[low], &arr[high]);
}
if (arr[high] < arr[mid]) {
swap(&arr[mid], &arr[high]);
}
// 此时,arr[mid]就是三个元素中的中位数
// 返回中位数的索引
return mid;
}
// 三数取中法选择基准快速排序
void MidQuickSort(int arr[], int low, int high) {
if (low < high) {
// 1. 使用三数取中法选择基准,并交换到起始位置
int midIndex = medianOfThree(arr, low, high);
swap(&arr[low], &arr[midIndex]);
// 2. 进行分区操作
int pivotIndex = Partition(arr, low, high);
// 3. 递归排序左右子数组
MidQuickSort(arr, low, pivotIndex - 1);
MidQuickSort(arr, pivotIndex + 1, high);
}
// 当 low >= high 时,递归终止
}六.知识回顾与重要考点
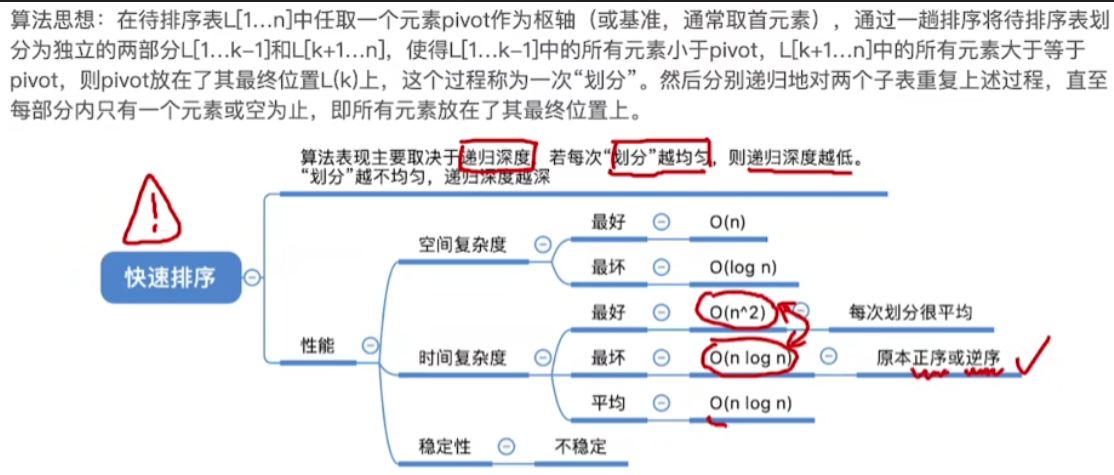
注:408原题中说,对所有尚未确定最终位置的所有元素进行一遍处理称为"一趟"排序,因此一次"划分"≠一趟排序。一次划分可以确定一个元素的最终位置,而一趟排序也许可以确定多个元素的最终位置。
结语
八更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页

