【动态规划】01背包与完全背包问题详解，LeetCode零钱兑换II秒解，轻松解力扣

👨‍💻程序员三明治 ：个人主页
🔥 个人专栏 : 《设计模式精解》《重学数据结构》

🤞先做到再看见！

01背包题目分析

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是O(2^n)，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

在下面的讲解，我举一个例子：

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

01背包解决方法

递归五部曲：

确定dp数组以及下标的含义：dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少

为什么需要用二维数组呢？因为有两个维度需要分别表示：物品和背包容量

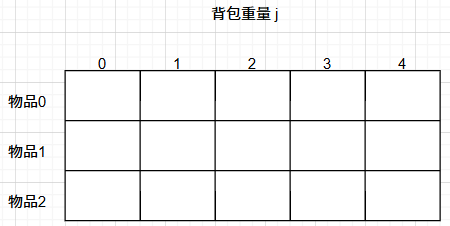
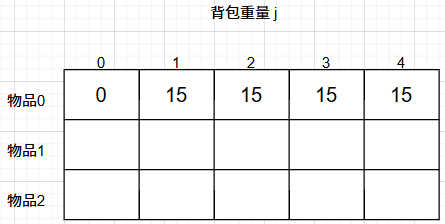
我们先看把物品0 放入背包的情况：

再看把物品1 放入背包：

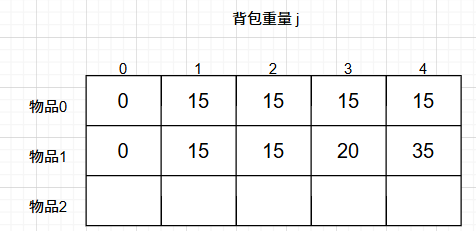
背包容量为 0，放不下物品0 或者物品1，此时背包里的价值为0。

背包容量为 1，只能放下物品0，背包里的价值为15。

背包容量为 2，只能放下物品0，背包里的价值为15。

背包容量为 3，上一行同一状态，背包只能放物品0，这次也可以选择物品1了，背包可以放物品1 或者物品0，物品1价值更大，背包里的价值为20。

背包容量为 4，上一行同一状态，背包只能放物品0，这次也可以选择物品1了，背包可以放下物品0 和物品1，背包价值为35。

确定递推公式

对于递推公式，首先我们要明确有哪些方向可以推导出 dp[i][j]

这里我们dp[1][4]的状态来举例：

求取 dp[1][4] 有两种情况：

放物品1
还是不放物品1

如果不放物品1，那么背包的价值应该是 dp[0][4] 即容量为4的背包，只放物品0的情况。

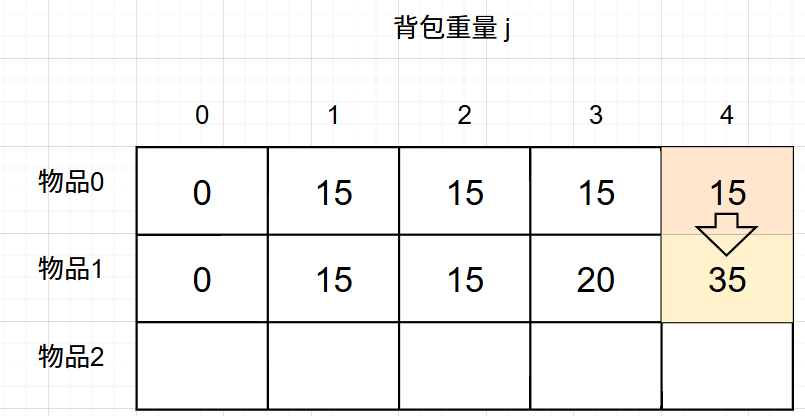
如果放物品1， 那么背包要先留出物品1的容量，目前容量是4，物品1 的容量（就是物品1的重量）为3，此时背包剩下容量为1。

容量为1，只考虑放物品0 的最大价值是 dp[0][1]，这个值我们之前就计算过。

所以放物品1 的情况 = dp[0][1] + 物品1 的价值，推导方向如图：

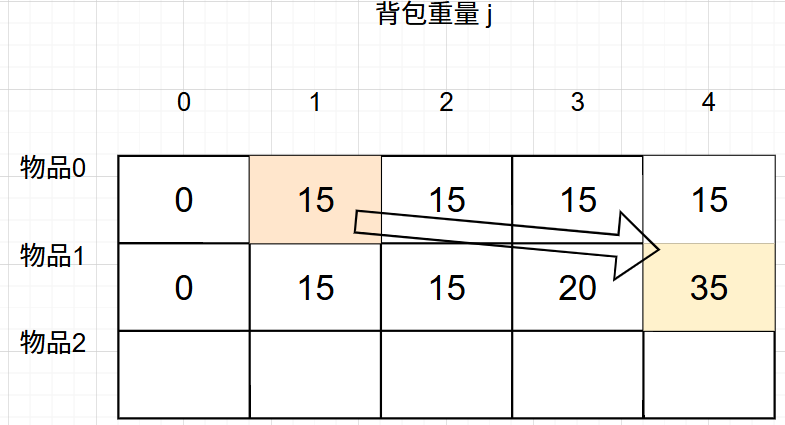
所以两种情况综合一起可以得出：

递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

dp数组初始化

首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：

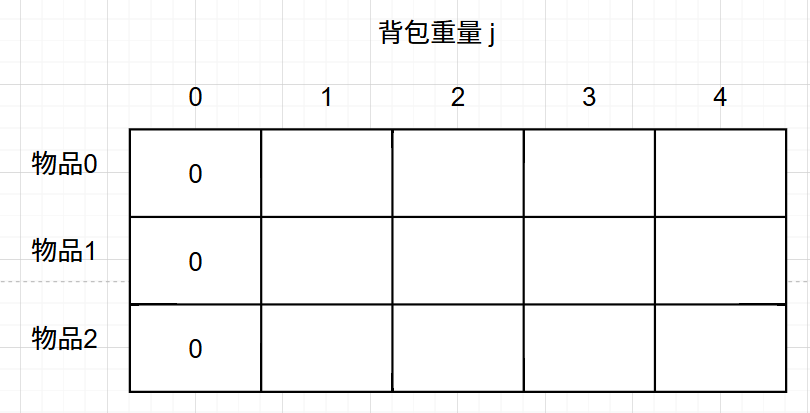
从递归公式可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

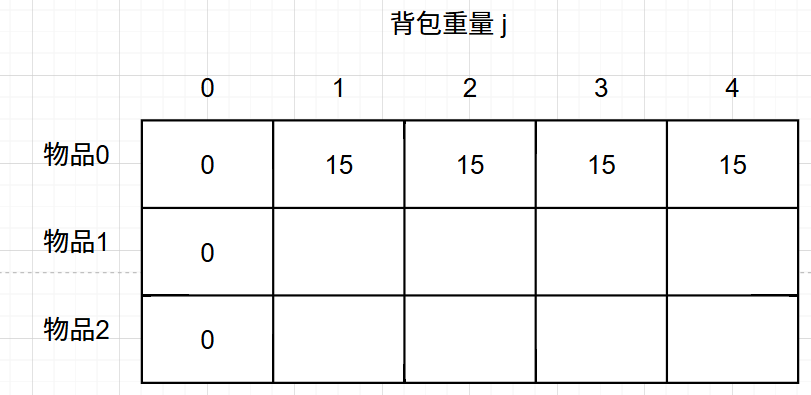
确定遍历顺序

先遍历物品还是先遍历背包重量呢？

其实都可以！！但是先遍历物品更好理解。

那么我先给出先遍历物品，然后遍历背包重量的代码。

java 复制代码

for (int i = 1; i < n; i++) {
    for (int j = 0; j <= bagweight; j++) {
        if (j < weight[i]) {
            dp[i][j] = dp[i - 1][j];
        } else {
            dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
}

举例推导dp数组

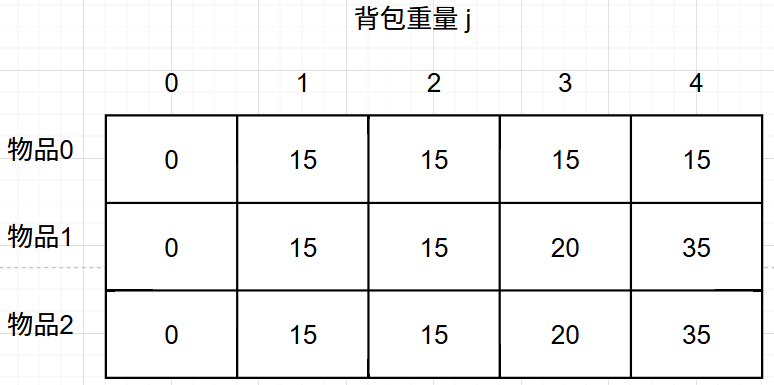
最终结果就是dp[2][4]。

完全背包题目分析

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

在下面的讲解，继续用之前的例子：

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

完全背包解决方法

确定dp数组以及下标的含义

dp[i][j] 表示从下标为[0-i]的物品，每个物品可以取无限次，放进容量为j的背包，价值总和最大是多少。

确定递推公式

这里依然拿dp[1][4]的状态来举例

求取 dp[1][4] 有两种情况：

放物品1
还是不放物品1

如果不放物品1，那么背包的价值应该是 dp[0][4] 即容量为4的背包，只放物品0的情况。

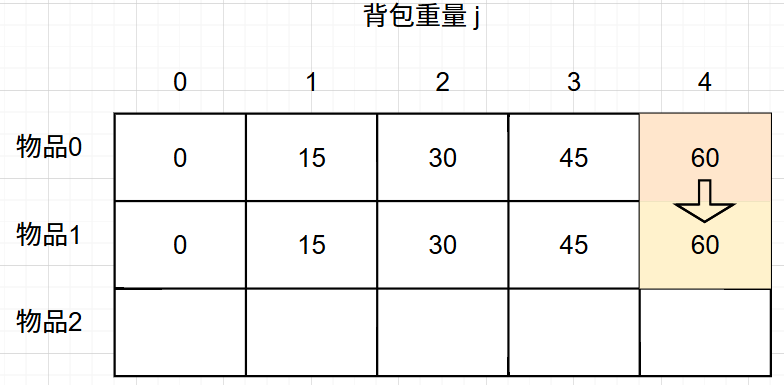
如果放物品1， 那么背包要先留出物品1的容量，目前容量是4，物品1 的容量（就是物品1的重量）为3，此时背包剩下容量为1。

容量为1，只考虑放物品0 和物品1 的最大价值是 dp[1][1]， 注意这里和01背包有所不同了！

在 01背包中，背包先空留出物品1的容量，此时容量为1，只考虑放物品0的最大价值是 dp[0][1]，因为01背包每个物品只有一个，既然空出物品1，那背包中也不会再有物品1！

而在完全背包中，物品是可以放无限个，所以即使空出物品1空间重量，那背包中也可能还有物品1，所以此时我们依然考虑放物品0 和物品1 的最大价值即： dp[1][1]，而不是 dp[0][1]

、

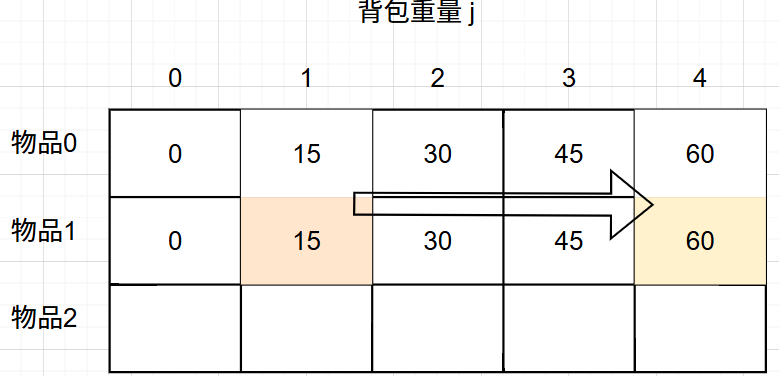所以可以得出

递推公式： dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);

dp数组初始化

如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0

再看其他情况：dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); 可以看出有一个方向 i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

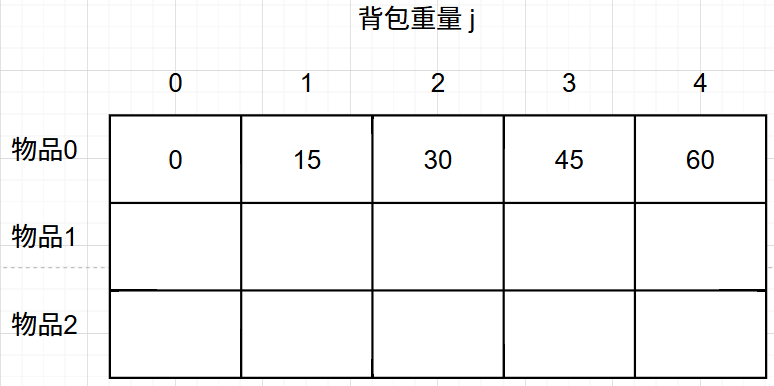
dp[0][j]，即：存放物品0的时候，各个容量的背包所能存放的最大价值。

java 复制代码

for (int j = weight[0]; j <= bagWeight; j++) {
    dp[0][j] = dp[0][j - weight[0]] + value[0];
}

确定遍历顺序

01背包二维DP数组，先遍历物品还是先遍历背包都是可以的。

因为两种遍历顺序，对于二维dp数组来说，递推公式所需要的值，二维dp数组里对应的位置都有。

举例推导dp数组

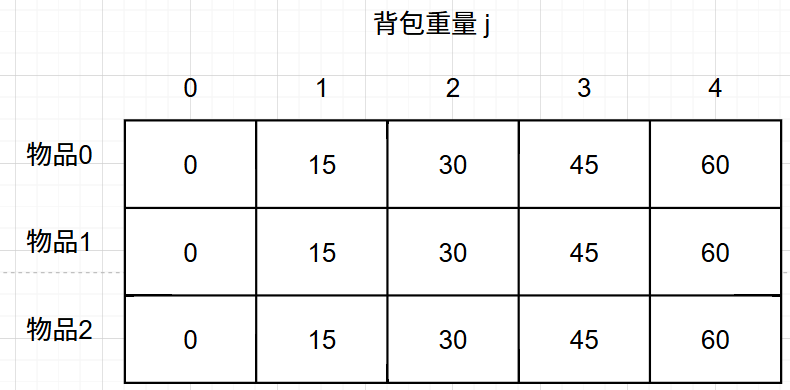
LeetCode 518.零钱兑换II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

plain 复制代码

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

plain 复制代码

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

思路

本题求的是装满这个背包的物品组合数是多少。因为每一种面额的硬币有无限个，所以这是完全背包。

动规五部曲

确定dp数组以及下标的含义：

dp[i][j]：使用下标为[0, i]的coins[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种组合方法。

递推公式

因为本题属于完全背包问题，所以递推公式需要参考

dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])

但考虑到我们的dp数组含义求的是组合个数，所以本题的递推公式是

dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]

初始化

以这个为例

第一行如何初始化？

dp[0][0] 应该是多少？

背包空间为0，装满「物品0」的组合数有多少呢？应该是 0 个，但如果「物品0」的数值就是0呢？岂不是可以有无限个0 组合和为0！

题目描述中说了1 <= coins.length <= 300和 1 <= coins[i] <= 5000，所以不用考虑物品数值为0的情况。

dp[0][j]的含义：用「物品0」（即coins[0]）装满背包容量为j的背包，有几种组合方法。

如果 j 可以整除物品0，那么装满背包就有1种组合方法。

java 复制代码

for (int j = 0; j <= amount; j++) {
    if (j % coins[0] == 0) dp[0][j] = 1;
}

最左列如何初始化呢？

dp[i][0] 的含义：用物品i（即coins[i]）装满容量为0的背包有几种组合方法。

都有一种方法，即不装。

所以 dp[i][0] 都初始化为1

综上，可以得出下图：

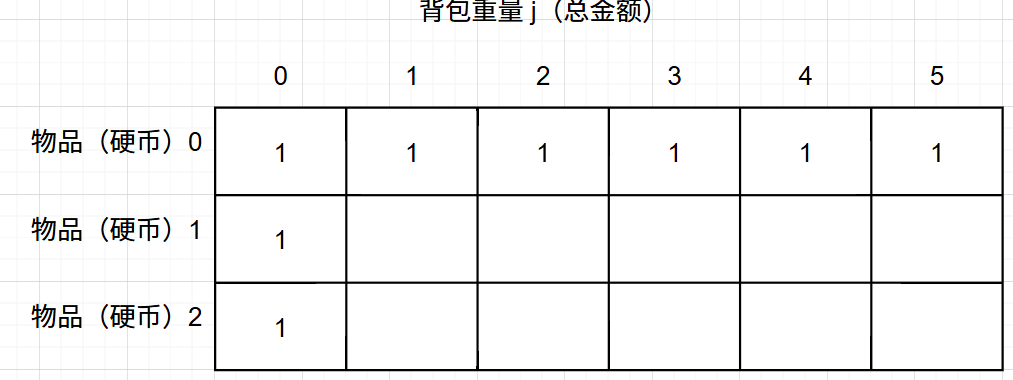
确定遍历顺序

先遍历物品，在遍历背包比较容易理解

打印dp数组

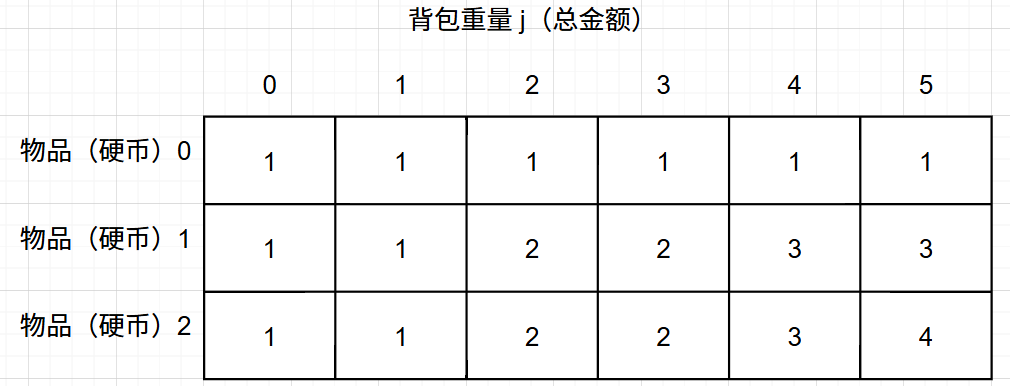
代码实现

java 复制代码

class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length][amount + 1];
        // 初始化最左列
        for (int i = 0; i < coins.length; i++) {
            dp[i][0] = 1;
        }
        // 初始化最上行
        for (int j = 0; j <= amount; j++) {
            if (j % coins[0] == 0) dp[0][j] = 1;
        }
        // 开始遍历
        for (int i = 1; i < coins.length; i++) {
            for (int j = 0; j <= amount; j++) {
                if (coins[i] > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
                }
            }
        }
        return dp[coins.length - 1][amount];
    }
}

如果我的内容对你有帮助，请辛苦动动您的手指为我点赞，评论，收藏。感谢大家!!

【动态规划】01背包与完全背包问题详解，LeetCode零钱兑换II秒解，轻松解力扣

目录

01背包题目分析

01背包解决方法

完全背包题目分析

完全背包解决方法

LeetCode 518.零钱兑换II

思路

代码实现