眼里没有对纪念日的专属感言,只有对优质内容诞生的渴望!!!
-
- 一、研究背景与意义
-
- [举例子理解 已知环境模型:机器人在 3 个房间中移动 ! ! !](#举例子理解 已知环境模型:机器人在 3 个房间中移动 ! ! !)
- [二、Q-learning 的核心思想](#二、Q-learning 的核心思想)
-
- [状态-动作价值函数( Q Q Q 函数)](#状态-动作价值函数( Q Q Q 函数))
- [三、Q-learning 的更新公式(核心公式)](#三、Q-learning 的更新公式(核心公式))
- [四、Q-learning 的算法流程](#四、Q-learning 的算法流程)
-
- [Q-learning 示例:冻结湖泊 ! ! !](#Q-learning 示例:冻结湖泊 ! ! !)
- [五、理论基础与收敛性(Watkins 的重要贡献)](#五、理论基础与收敛性(Watkins 的重要贡献))
- [六:Q-learning 的常见问题](#六:Q-learning 的常见问题)
-
- [Q-learning 的缺点是什么?](#Q-learning 的缺点是什么?)
- [为什么 Q-learning 称为 Q-learning?](#为什么 Q-learning 称为 Q-learning?)
- [为什么 Q-learning 是 off-policy 的?](#为什么 Q-learning 是 off-policy 的?)
- [Q-learning 总是会收敛吗?](#Q-learning 总是会收敛吗?)
- [为什么需要深度 Q-learning?](#为什么需要深度 Q-learning?)
1989 年,Christopher J. C. H. Watkins 在其博士论文中系统提出并分析了 Q-learning 算法 , 开创 无模型(model-free)强化学习 理论体系,为智能体在 未知环境 中通过试错交互直接学习最优状态-动作价值函数。
一、研究背景与意义
- 80 年代以前的强化学习 = 已知 MDP + 动态规划 + 解 Bellman 方程
- Watkins 的 Q-learning = 未知环境 + 交互采样 + 收敛保证
在 20 世纪 80 年代以前,强化学习研究多依赖于 已知环境模型(如马尔可夫决策过程 MDP 的转移概率与奖励函数),典型方法包括动态规划。
但在现实问题中:
- 环境模型往往 未知或难以精确建模
- 状态空间可能很大
- 只能通过与环境交互获得经验
Watkins 的核心贡献在于:
不需要已知环境模型,仅通过经验样本,就能在理论上保证收敛到最优策略。
这使强化学习真正具备了 "从试错中学习" 的能力。
举例子理解 已知环境模型:机器人在 3 个房间中移动 ! ! !
设想一个非常小的环境,
-
状态空间 (已知 ): S = { A , B , C } S = \{A, B, C\} S={A,B,C},其中 A A A 是起始房间, B B B 是中间房间, C C C 是目标房间(终止状态)。
-
动作空间 (已知 ),在每个非终止状态下,机器人可以选择: A = { Left , Right } A = \{\text{Left}, \text{Right}\} A={Left,Right}。
-
状态转移概率 (完全已知模型 ),这是 80 年代前方法的关键假设:
当前状态 动作 下一状态 概率 A A A Right \text{Right} Right B B B 1.0 1.0 1.0 A A A Left \text{Left} Left A A A 1.0 1.0 1.0 B B B Right \text{Right} Right C C C 1.0 1.0 1.0 B B B Left \text{Left} Left A A A 1.0 1.0 1.0 没有随机性,一切都事先知道。
-
奖励函数 (已知 ):
R ( s , a , s ′ ) = { + 10 , s ′ = C − 1 , 其他情况 R(s,a,s') = \begin{cases}+10, & s' = C \\ -1, & \text{其他情况} \end{cases} R(s,a,s′)={+10,−1,s′=C其他情况 -
折扣因子 (已知 ): γ = 0.9 \gamma = 0.9 γ=0.9
下面用动态规划(Value Iteration)求解,这是 典型的"已知模型 + 动态规划" 方法。
-
定义 状态价值函数 : V ( s ) = max π E [ ∑ t = 0 ∞ γ t r t + 1 ∣ s 0 = s ] V(s) = \max_\pi \mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t r_{t+1} \mid s_0 = s\right] V(s)=πmaxE[t=0∑∞γtrt+1∣s0=s]
-
Bellman 最优方程 (核心),由于模型已知,可以直接写出: V ( s ) = max a ∑ s ′ P ( s ′ ∣ s , a ) [ R ( s , a , s ′ ) + γ V ( s ′ ) ] V(s) = \max_a \sum_{s'} P(s'|s,a)\big[ R(s,a,s') + \gamma V(s') \big] V(s)=amaxs′∑P(s′∣s,a)[R(s,a,s′)+γV(s′)]
-
手工展开计算
-
终止状态 C C C, V ( C ) = 0 V(C) = 0 V(C)=0
-
状态 B B B,
- Right \text{Right} Right → C C C: Q ( B , Right ) = 10 + 0.9 ⋅ 0 = 10 Q(B,\text{Right}) = 10 + 0.9 \cdot 0 = 10 Q(B,Right)=10+0.9⋅0=10
- Left \text{Left} Left → A A A: Q ( B , Left ) = − 1 + 0.9 V ( A ) Q(B,\text{Left}) = -1 + 0.9 V(A) Q(B,Left)=−1+0.9V(A)
V ( B ) = max ( 10 , − 1 + 0.9 V ( A ) ) V(B) = \max(10, -1 + 0.9 V(A)) V(B)=max(10,−1+0.9V(A))
-
状态 A A A,
- Right \text{Right} Right → B B B: Q ( A , Right ) = − 1 + 0.9 V ( B ) Q(A,\text{Right}) = -1 + 0.9 V(B) Q(A,Right)=−1+0.9V(B)
- Left \text{Left} Left → A A A: Q ( A , Left ) = − 1 + 0.9 V ( A ) Q(A,\text{Left}) = -1 + 0.9 V(A) Q(A,Left)=−1+0.9V(A)
V ( A ) = max ( − 1 + 0.9 V ( B ) , − 1 + 0.9 V ( A ) ) V(A) = \max(-1 + 0.9 V(B), -1 + 0.9 V(A)) V(A)=max(−1+0.9V(B),−1+0.9V(A))
-
-
联立方程求解 ,由于最优策略显然是一直向右走,我们可直接验证:
V ( B ) = 10 , V ( A ) = − 1 + 0.9 ⋅ 10 = 8 V(B) = 10, \quad V(A) = -1 + 0.9 \cdot 10 = 8 V(B)=10,V(A)=−1+0.9⋅10=8 -
得到最优策略 (无需试错)
π ∗ ( A ) = Right , π ∗ ( B ) = Right \pi^*(A) = \text{Right}, \quad \pi^*(B) = \text{Right} π∗(A)=Right,π∗(B)=Right
📌 整个过程完全没有与环境交互、没有采样、没有试错。
如果用 Q-learning 会怎样?
- 不需要知道 Right \text{Right} Right 一定到 B B B;不需要知道奖励函数形式
- 只需要:执行动作、观察结果、更新 Q Q Q 值
这正是 Watkins 在 1989 年的革命性突破。
二、Q-learning 的核心思想
- 间接学习(80 年代前):像是在先写游戏说明书,再通关
- 直接学习 (Q-learning):不管环境规则是什么,直接记住 "在这个状态下做这个动作,将来能赚多少分"
基于模型的算法使用转移函数和奖励函数来估计最优策略并构建模型。相反,无模型算法 通过 经验 学习其 行动的后果 ,而 不依赖转移函数和奖励函数。
Q-learning 的关键思想是:
- 不学习环境模型(转移概率、奖励函数)
- 直接逼近最优 Q Q Q 函数
- 采用"贪婪目标 + 任意行为策略"进行学习
这使它成为一种 off-policy 强化学习算法。
状态-动作价值函数( Q Q Q 函数)
Q-learning 是一种无模型、基于价值的算法,它将在基于智能体当前状态的基础上找到最佳的动作序列。"Q" 代表 quality(质量)。quality 表示该动作在最大化未来奖励方面的价值。
状态-动作价值函数 Q ( s , a ) Q(s,a) Q(s,a):是指智能体 在状态 s s s 开始,随后遵循策略 π \pi π 采取动作 a a a 时所期望获得的回报 。可以将 策略 π \pi π 描述为代理 根据当前状态 s s s 选择特定动作的策略。
Q ( s , a ) Q(s,a) Q(s,a) 告诉代理在特定状态 s s s 下可能动作 a a a 的价值 。给定状态 s s s ,状态-动作价值函数 计算该状态中每个可能动作 a i a_i ai 的价值,返回标量值。价值越高表示相对于给定目标的动作越好。
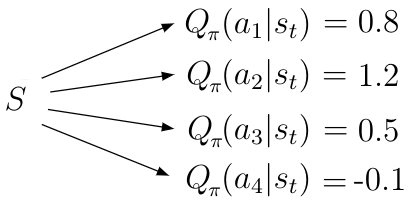
如果在 Q ( s , a ) Q(s,a) Q(s,a) 中执行期望算子 E E E,就会得到一个 涉及概率的动作价值函数的新形式。
在强化学习中,Q-learning 直接学习 状态-动作价值函数 :
Q ∗ ( s , a ) = E [ ∑ t = 0 ∞ γ t r t + 1 ∣ s 0 = s , a 0 = a , π ∗ ] Q^*(s,a) = \mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t r_{t+1} \mid s_0=s, a_0=a, \pi^*\right] Q∗(s,a)=E[t=0∑∞γtrt+1∣s0=s,a0=a,π∗]含义:在状态 s s s 下采取动作 a a a,并在此后始终执行 最优策略 所能获得的期望折扣回报。
一旦得到 Q ∗ ( s , a ) Q^*(s,a) Q∗(s,a),最优策略可直接由: π ∗ ( s ) = arg max a Q ∗ ( s , a ) \pi^*(s) = \arg\max_a Q^*(s,a) π∗(s)=argmaxaQ∗(s,a) 得到。
三、Q-learning 的更新公式(核心公式)
Watkins 提出的 Q-learning 更新规则 如下:
Q ( s t , a t ) ← Q ( s t , a t ) + α [ r t + 1 + γ max a ′ Q ( s t + 1 , a ′ ) − Q ( s t , a t ) ] Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \Big[ r_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t) \Big] Q(st,at)←Q(st,at)+α[rt+1+γa′maxQ(st+1,a′)−Q(st,at)]
各项解释:
- s t , a t s_t, a_t st,at:当前状态与动作
- r t + 1 r_{t+1} rt+1:执行动作后获得的 即时奖励
- s t + 1 s_{t+1} st+1:下一状态
- α \alpha α:学习率(learning rate)
- γ \gamma γ:折扣因子(discount factor)
- max a ′ Q ( s t + 1 , a ′ ) \max_{a'} Q(s_{t+1}, a') maxa′Q(st+1,a′):对下一状态采取最优动作的估计回报
📌 关键点 :即使当前执行的动作不是最优的,更新时仍然假设"下一步采取最优动作",这正是 off-policy 的本质。
四、Q-learning 的算法流程
典型 Q-learning 算法步骤如下:
-
初始化 :对所有状态-动作对,初始化 Q ( s , a ) Q(s,a) Q(s,a)(通常为 0 或随机值)
-
重复以下过程(每个 episode)
- 初始化状态 s s s
- 在状态 s s s 下,根据某种行为策略(如 ε \varepsilon ε-greedy)选择动作 a a a
- 执行动作,观察奖励 r r r 和下一状态 s ′ s' s′
- 按 Q-learning 更新公式更新 Q ( s , a ) Q(s,a) Q(s,a)
- 令 s ← s ′ s \leftarrow s' s←s′
- 若到达终止状态,结束 episode
-
最终策略 : π ( s ) = arg max a Q ( s , a ) \pi(s) = \arg\max_a Q(s,a) π(s)=argmaxaQ(s,a)
Q-learning 示例:冻结湖泊 ! ! !
通过冻结湖泊的示例详细学习 Q Q Q 学习的工作原理,在这个环境中,智能体必须从起点穿过冻结的湖面到达目标点,且不能掉进洞里。最佳策略是走最短路径以到达目标。

- Q Q Q-Table :智能体将使用 Q Q Q 表 根据环境中每个状态的期望奖励选择最佳动作。简单来说, Q Q Q 表是一个由动作和状态集合构成的数据结构,使用 Q Q Q 学习算法来 更新表中的数值。
- Q-Function : Q Q Q 函数 使用贝尔曼方程,以状态 s s s 和动作 a a a 为输入。该方程简化了状态值和状态-动作值的计算。
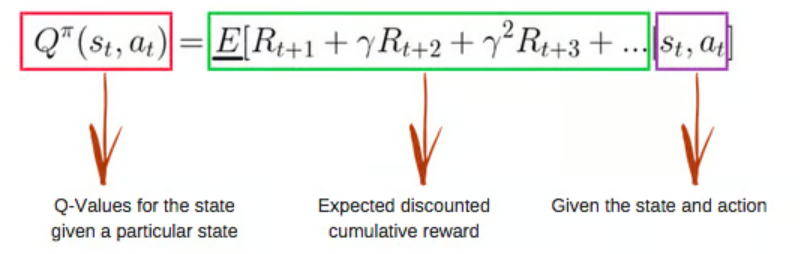
- Q-learning algorithm :
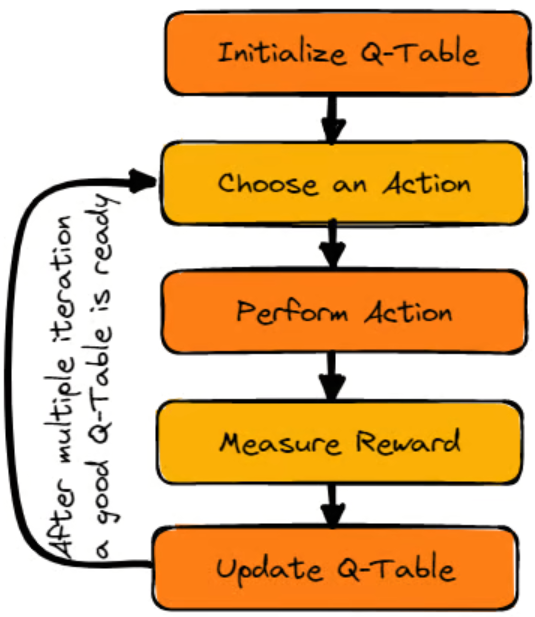
-
Initialize Q Q Q-Table 。根据 动作 的数量构建 列 ,根据 状态 的数量构建 行 。
示例中,角色可以向上、向下、向左、向右移动。有四个可能的动作和四个状态(开始、空闲、错误路径和结束)。也可以将错误路径视为掉入洞中。把 Q Q Q 表的初始值设为 0 。
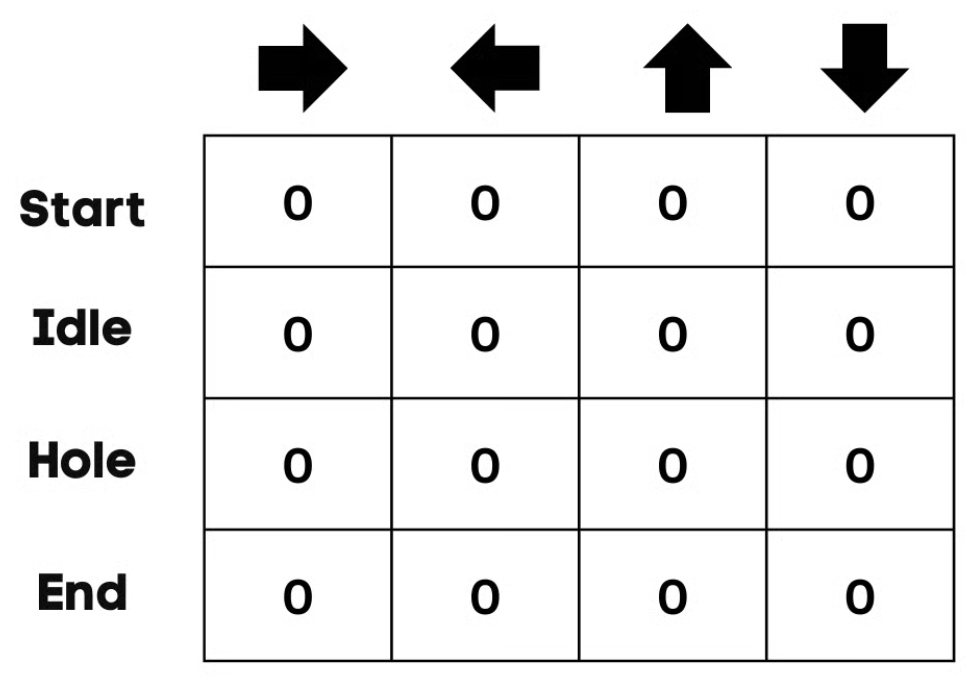
-
Choose an Action 。开始时,智能体会选择 执行随机动作 (向下或向右),在第二次运行时,它将 使用更新后的 Q Q Q 表来选择动作。
-
Perform an Action 。选择一个动作并执行该动作将会重复多次,直到训练循环停止 。
第一次的动作和状态是使用 Q Q Q 表选取的。在案例中, Q Q Q 表的所有数值均为零。
然后,智能体将向下移动,并 使用贝尔曼方程更新 Q Q Q 表 。每一次移动,都会更新 Q Q Q 表中的数值,同时利用它来决定最佳的行动方案 。
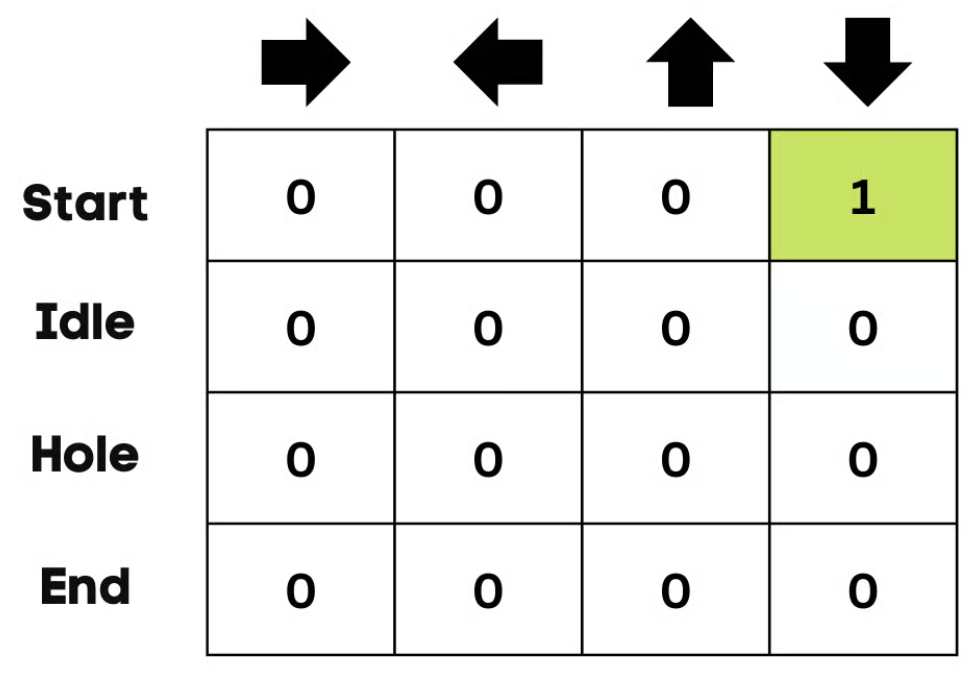
最初,智能体处于 探索模式 ,会随机选择一个动作来探测环境。ε ε ε‑贪婪策略 是一种平衡探索与利用的简单方法。 ε ε ε 代表 选择探索的概率,而在探索机会较小的情况下则进行利用。
一开始,epsilon 率较高,意味着智能体处于探索模式。随着对环境的探索,epsilon 会下降,智能体开始利用环境。在探索过程中,随着每一次迭代,智能体对 Q Q Q 值的估计变得更加自信。
-
Measuring the Rewards 。采取行动后,会测量结果和奖励。
达成目标的奖励为 +1。走错路径(掉入洞中)的奖励为 0。在冰湖上保持静止或移动的奖励也是 0。
-
Update Q-Table 。使用该公式更新函数 Q ( S t , A t ) Q(S_t , A_t ) Q(St,At)。它使用上一步估计的 Q Q Q 值、学习率和时序差分误差。时序差分误差通过即时奖励、折扣后的最大预期未来奖励以及先前的估计 Q Q Q 值计算得到。该过程会 重复多次,直至 Q Q Q 表得到更新且 Q Q Q 值函数达到最大化 。
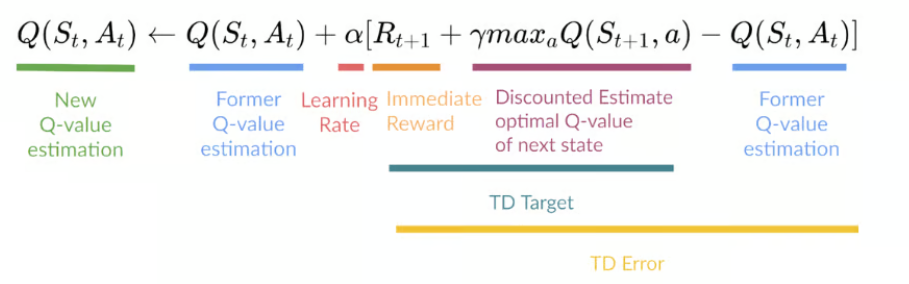
一开始,智能体在探索环境以更新 Q-Table。当 Q-Table 准备好后,智能体将开始利用并做出更好的决策。
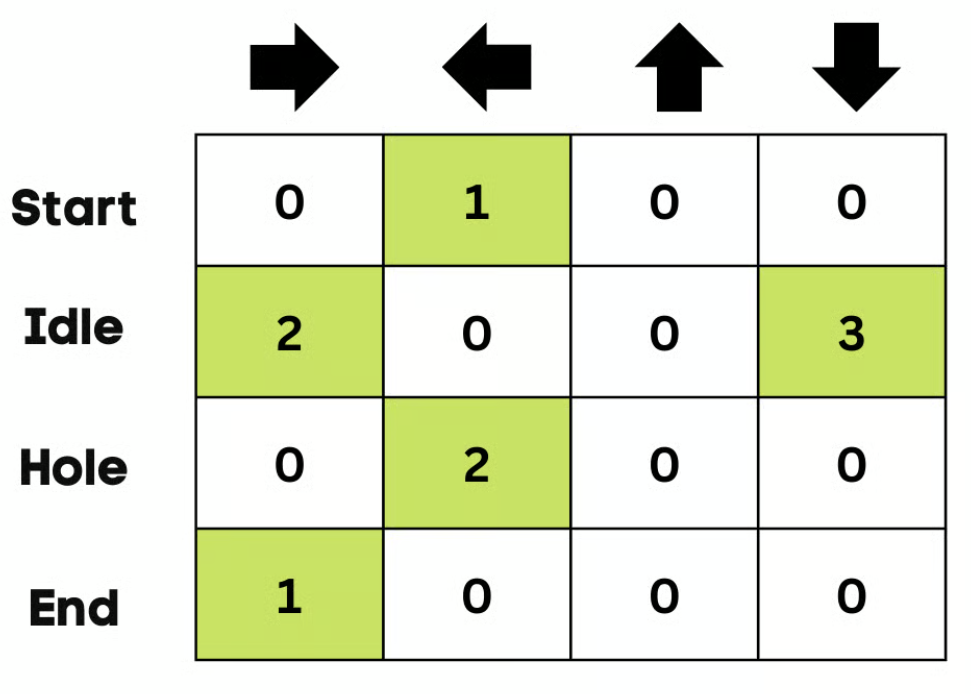
在冻结湖的情形下,智能体会学习走最短路径以到达目标,并避免掉进洞里。
-
五、理论基础与收敛性(Watkins 的重要贡献)
Watkins 在理论上证明了:
在以下条件下,Q-learning 几乎必然收敛 到最优 Q Q Q 函数 Q ∗ Q^* Q∗:
- 所有状态-动作对被 无限次访问
- 学习率满足 Robbins--Monro 条件: ∑ t α t = ∞ , ∑ t α t 2 < ∞ \sum_t \alpha_t = \infty,\quad \sum_t \alpha_t^2 < \infty ∑tαt=∞,∑tαt2<∞
- 环境是有限状态、有限动作的 MDP
- 折扣因子 γ < 1 \gamma < 1 γ<1
这是 无模型强化学习中首个具有严格收敛性证明的算法之一。
没有 1989 年的 Q-learning,就没有后来的深度强化学习浪潮。
Watkins 的 Q-learning 直接催生了大量后续研究:
- 表格型强化学习的标准算法
- Deep Q-Network (DQN):用神经网络近似 Q 函数(DeepMind, 2013)
- Double Q-learning、Dueling DQN、Prioritized Replay 等改进
- 成为现代深度强化学习的理论起点之一
六:Q-learning 的常见问题
Q-learning 的缺点是什么?
在 Q-learning 中,学习过程对智能体来说成本很高,尤其是在最初的步骤。
为什么会这样?
为了收敛到最优策略,需要频繁访问每一个状态和动作对。
为什么 Q-learning 称为 Q-learning?
在 Q-learning 中,'Q' 代表 quality,它代表给定动作在实现未来奖励方面的有用程度,用于创建状态与动作的映射系统,以最大化期望奖励。
为什么 Q-learning 是 off-policy 的?
在 Q-learning 中,更新后的策略不同于动作策略,这也是它被称为 off-policy 算法的原因。
Q-learning 总是会收敛吗?
是的。在训练过程中,算法总是会收敛到最优策略。
为什么需要深度 Q-learning?
Q-learning 是一种针对较小且离散环境设计的简单算法。
若面对更大的环境,将需要一个极其庞大的 状态-动作 Q Q Q 表,这会占用更多的内存并且在训练时需要更大的计算量。
而深度 Q-learning 则用神经网络取代 Q Q Q 表,以处理包含连续动作和状态的大型环境。