【算法基础篇】（四十）数论之算术基本定理深度剖析：从唯一分解到阶乘分解

---

目录

前言

[一、算术基本定理：数论的 "万能钥匙"](#一、算术基本定理：数论的 “万能钥匙”)

[1.1 定理的核心内涵](#1.1 定理的核心内涵)

[1.2 定理的实际意义](#1.2 定理的实际意义)

[1.3 一个直观的例子](#1.3 一个直观的例子)

二、质因数分解：试除法的优化与实现

[2.1 试除法的核心思路](#2.1 试除法的核心思路)

[2.2 避免溢出的关键技巧](#2.2 避免溢出的关键技巧)

[2.3 C++ 实现试除法分解质因数](#2.3 C++ 实现试除法分解质因数)

[2.4 代码测试与分析](#2.4 代码测试与分析)

三、进阶优化：结合素数筛的质因数分解

[3.1 优化原理](#3.1 优化原理)

[3.2 结合线性筛的分解实现](#3.2 结合线性筛的分解实现)

[3.3 适用场景](#3.3 适用场景)

[四、实战例题 1：洛谷 P2043 质因子分解（N! 分解）](#四、实战例题 1：洛谷 P2043 质因子分解（N! 分解）)

[4.1 题目分析](#4.1 题目分析)

[4.2 阶乘分解的关键公式](#4.2 阶乘分解的关键公式)

[4.3 解法实现（试除法 + 公式）](#4.3 解法实现（试除法 + 公式）)

[4.4 优化解法（线性筛 + 公式）](#4.4 优化解法（线性筛 + 公式）)

[4.5 两种解法对比](#4.5 两种解法对比)

[五、实战例题 2：洛谷 P10495 阶乘分解（强化版）](#五、实战例题 2：洛谷 P10495 阶乘分解（强化版）)

[5.1 题目分析](#5.1 题目分析)

[5.2 优化代码实现](#5.2 优化代码实现)

[5.3 关键优化点](#5.3 关键优化点)

六、算术基本定理的延伸应用

[6.1 约数个数定理](#6.1 约数个数定理)

[6.2 约数和定理](#6.2 约数和定理)

[6.3 最大公约数与最小公倍数](#6.3 最大公约数与最小公倍数)

七、常见误区与避坑指南

[7.1 数值溢出问题](#7.1 数值溢出问题)

[7.2 边界条件处理](#7.2 边界条件处理)

[7.3 效率优化误区](#7.3 效率优化误区)

总结

---

前言

在算法竞赛的数论领域，算术基本定理是当之无愧的 "基石定理"。它看似简单 ------ 每个大于 1 的自然数都能唯一分解为质数乘积，但由此延伸出的质因数分解、阶乘分解等问题，却贯穿了从入门到进阶的各类竞赛题目。本文将从定理本质出发，层层拆解质因数分解的核心思路，详解试除法的优化技巧，手把手教你掌握阶乘分解的高效解法，让你在数论题目中轻松举一反三。下面就让我们正式开始吧！

---

一、算术基本定理：数论的 "万能钥匙"

1.1 定理的核心内涵

算术基本定理（又称唯一分解定理）指出：任何一个大于 1 的自然数 n，都可以唯一分解成有限个质数的乘积，形式如下：n=p1α1​​×p2α2​​×p3α3​​×⋯×pkαk​​其中 p1​<p2​<p3​<⋯<pk​ 均为质数，α1​,α2​,...,αk​ 是正整数（称为质因子的指数），这样的分解称为 n 的标准分解式。

这个定理的关键在于 "唯一" 二字 ------ 无论你从哪个角度分解，最终得到的质因子种类和对应的指数都是固定的。比如 12 的分解式只能是 22×31，不可能出现 21×32 或其他形式。

1.2 定理的实际意义

算术基本定理之所以重要，是因为它将任意一个复杂的自然数，拆解成了最基本的 "质数积木"。就像乐高积木可以拼出各种造型，质数通过不同的组合（乘积）和重复次数（指数），构成了所有大于 1 的自然数。

在算法竞赛中，这个定理是解决以下问题的核心工具：

• 质因数分解：将一个数拆分为标准分解式（如竞赛题中常见的 "分解 x 的质因数"）；
• 约数相关问题：求约数个数、约数和（基于分解式的公式推导）；
• 阶乘分解：计算 N! 的质因数组成（如 "求 10! 包含多少个质因子 2"）；
• 最大公约数 / 最小公倍数：通过分解式快速计算 gcd 和 lcm（gcd 取最小指数，lcm 取最大指数）。

1.3 一个直观的例子

我们以 360 为例，看看它的标准分解过程：

1. 360 ÷ 2 = 180（2 是最小质数，也是 360 的最小质因子）；
2. 180 ÷ 2 = 90（继续除以 2，直到不能整除）；
3. 90 ÷ 2 = 45（此时 2 的指数为 3）；
4. 45 ÷ 3 = 15（下一个质因子是 3）；
5. 15 ÷ 3 = 5（3 的指数为 2）；
6. 5 ÷ 5 = 1（最后一个质因子是 5，指数为 1）。

最终得到 360 的标准分解式：23×32×51，这正是算术基本定理的直观体现。

二、质因数分解：试除法的优化与实现

质因数分解是算术基本定理的直接应用，核心任务是找到一个数的所有质因子及其指数。最常用的方法是试除法，看似暴力，却能通过优化达到极高的效率。

2.1 试除法的核心思路

试除法的本质的是 "枚举可能的质因子，逐一验证并分解"。根据算术基本定理，我们可以得到两个关键优化点：

1. 枚举范围优化：对于 n 的质因子，必然有一个不大于n（如果 n 有大于n的质因子，那么它对应的另一个因子必然小于n，早已被枚举到）；
2. 重复除法优化：找到一个质因子 p 后，要将 n 中所有的 p 都除尽，并记录次数（即指数），避免重复枚举。

举个例子，分解 n=100：

• 100=10，只需枚举 2 到 10 的数；
• 2 能整除 100，100 ÷ 2 = 50，50 ÷ 2 = 25，此时 2 的指数为 2，n 变为 25；
• 3 不能整除 25，跳过；
• 4 不能整除 25（25 是奇数），跳过；
• 5 能整除 25，25 ÷ 5 = 5，5 ÷ 5 = 1，此时 5 的指数为 2，n 变为 1，分解结束；
• 最终分解式：22×52。

2.2 避免溢出的关键技巧

在代码实现中，枚举条件如果写成i <= sqrt(n)，可能会因为 sqrt 函数的精度问题出错；如果写成i * i <= n，当 i 接近 1e9 时，i*i 会超出 int 范围导致溢出。因此，推荐使用i <= n / i 的写法，既避免了精度问题，又防止了溢出。

2.3 C++ 实现试除法分解质因数

#include <iostream>
#include <unordered_map>
using namespace std;

// 分解质因数，返回质因子及其指数（键为质因子，值为指数）
unordered_map<int, int> prime_factor(int x) {
    unordered_map<int, int> factors;
    // 枚举到sqrt(x)即可
    for (int i = 2; i <= x / i; ++i) {
        if (x % i == 0) { // i是x的质因子
            int cnt = 0;
            while (x % i == 0) { // 除尽所有i
                cnt++;
                x /= i;
            }
            factors[i] = cnt;
        }
    }
    // 剩余的x如果大于1，说明是最后一个质因子（大于sqrt(原x)）
    if (x > 1) {
        factors[x] = 1;
    }
    return factors;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n;
    cin >> n;
    auto factors = prime_factor(n);
    // 按质因子从小到大输出
    cout << n << " = ";
    bool first = true;
    for (auto [p, cnt] : factors) {
        if (!first) cout << " × ";
        cout << p << "^" << cnt;
        first = false;
    }
    cout << endl;
    return 0;
}

2.4 代码测试与分析

输入：360

输出：360 = 2^3 × 3^2 × 5^1

时间复杂度 ：O (√n)。最坏情况下需要枚举到√n（如 n 是质数时），但实际情况中，由于每次分解都会将 n 大幅减小，实际运行时间远低于理论上限。对于 n≤1e12 的数，√n=1e6，枚举 1e6 次完全可以在毫秒级完成。

空间复杂度 ：O (k)，k 为 n 的质因子种类数（如 360 有 3 种质因子，k=3），空间开销可以忽略。

三、进阶优化：结合素数筛的质因数分解

当需要对多个数进行质因数分解时，逐一使用试除法的效率会偏低。此时可以先通过线性筛（欧拉筛） 预处理出范围内的所有质数，再用这些质数进行分解，进一步降低时间复杂度。

3.1 优化原理

线性筛可以在 O (n) 时间内筛选出 [2, n] 范围内的所有质数，并记录每个数的最小质因子（MPF，Minimum Prime Factor）。利用最小质因子，我们可以快速分解任意数 x：

1. 找到 x 的最小质因子 p；
2. 记录 p 的指数（将 x 中所有 p 除尽）；
3. x = x /p^k（k 为 p 的指数），重复步骤 1，直到 x=1。

这种方法的优势在于，无需枚举所有可能的因子，而是直接使用预处理好的最小质因子，分解效率可以提升至 O (log x)。

3.2 结合线性筛的分解实现

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;

const int MAXN = 1e6 + 10;
int min_prime[MAXN]; // 存储每个数的最小质因子
vector<int> primes;  // 存储所有质数

// 线性筛预处理最小质因子
void sieve(int n) {
    memset(min_prime, 0, sizeof min_prime);
    primes.clear();
    for (int i = 2; i <= n; ++i) {
        if (min_prime[i] == 0) { // i是质数
            min_prime[i] = i;
            primes.push_back(i);
        }
        // 枚举所有质数，更新i*primes[j]的最小质因子
        for (int j = 0; j < primes.size() && primes[j] <= min_prime[i] && i * primes[j] <= n; ++j) {
            min_prime[i * primes[j]] = primes[j];
        }
    }
}

// 利用最小质因子分解x
unordered_map<int, int> fast_prime_factor(int x) {
    unordered_map<int, int> factors;
    while (x > 1) {
        int p = min_prime[x]; // x的最小质因子
        int cnt = 0;
        while (x % p == 0) {
            cnt++;
            x /= p;
        }
        factors[p] = cnt;
    }
    return factors;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int max_range = 1e6;
    sieve(max_range); // 预处理1e6以内的最小质因子
    
    int n;
    while (cin >> n) {
        auto factors = fast_prime_factor(n);
        cout << n << " = ";
        bool first = true;
        for (auto [p, cnt] : factors) {
            if (!first) cout << " × ";
            cout << p << "^" << cnt;
            first = false;
        }
        cout << endl;
    }
    return 0;
}

3.3 适用场景

这种方法适用于多组数据分解的场景，例如：

• 输入 T 组测试用例，每组测试用例分解一个数 x（x≤1e6）；
• 对 [1, n] 范围内的所有数进行质因数分解（如后续的阶乘分解）。

预处理线性筛的时间是 O (max_range) ，之后每组分解的时间是 O (log x)，整体效率远高于多次单独使用试除法。

四、实战例题 1：洛谷 P2043 质因子分解（N! 分解）

题目链接：https://www.luogu.com.cn/problem/P2043

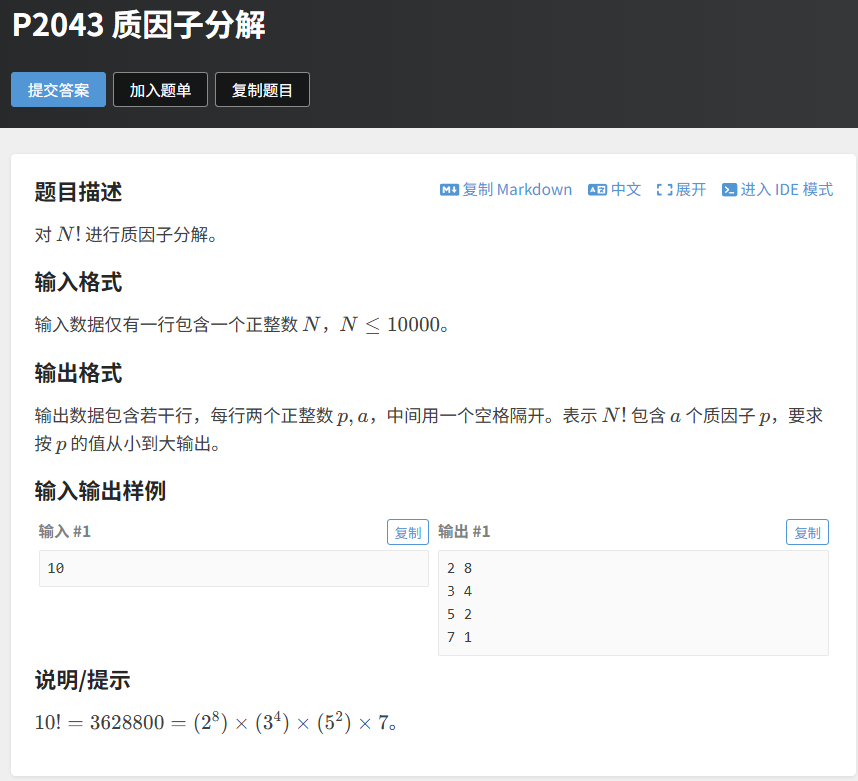
4.1 题目分析

题目描述：对 N! 进行质因子分解，输出每个质因子及其出现的次数（按质因子从小到大输出）。

输入：一个正整数 N（N≤1e4）。

输出：若干行，每行两个正整数 p 和 a，表示 N! 包含 a 个质因子 p。

示例：输入：10输出：2 83 45 27 1

核心难点：N! = 1×2×3×...×N，直接计算 N! 再分解会导致数值溢出（1e4! 是一个极其庞大的数，远超出 long long 范围），因此必须找到更巧妙的方法。

4.2 阶乘分解的关键公式

根据算术基本定理，N! 的质因子必然是 [2, N] 范围内的质数。对于每个质数 p，其在 N! 中的出现次数（指数）为：直到为止。

4.3 解法实现（试除法 + 公式）

#include <iostream>
#include <cstring>
using namespace std;

const int MAXN = 1e4 + 10;
int cnt[MAXN]; // cnt[p]表示质因子p在N!中的指数

// 试除法分解单个x的质因数，并累加指数到cnt数组
void decompose(int x) {
    for (int i = 2; i <= x / i; ++i) {
        while (x % i == 0) {
            cnt[i]++;
            x /= i;
        }
    }
    if (x > 1) {
        cnt[x]++;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int N;
    cin >> N;
    memset(cnt, 0, sizeof cnt);
    
    // 对1~N的每个数分解质因数，累加指数
    for (int i = 2; i <= N; ++i) {
        decompose(i);
    }
    
    // 输出所有有贡献的质因子（cnt[p]>0）
    for (int p = 2; p <= N; ++p) {
        if (cnt[p] > 0) {
            cout << p << " " << cnt[p] << endl;
        }
    }
    return 0;
}

4.4 优化解法（线性筛 + 公式）

对于 N≤1e6 的场景，上述解法的效率会偏低（时间复杂度 O (N√N)）。此时可以结合线性筛先筛选出 [2, N] 的所有质数，再用公式计算每个质数的指数，时间复杂度优化至 O (N log N)。

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;

const int MAXN = 1e6 + 10;
bool st[MAXN]; // 标记是否为合数
int primes[MAXN], cnt_primes; // 存储质数，cnt_primes为质数个数

// 线性筛筛选[2, n]的所有质数
void sieve(int n) {
    memset(st, false, sizeof st);
    cnt_primes = 0;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) {
            primes[++cnt_primes] = i;
        }
        for (int j = 1; 1LL * i * primes[j] <= n; ++j) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) {
                break;
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int N;
    cin >> N;
    sieve(N); // 筛选[2, N]的所有质数
    
    // 对每个质数计算其在N!中的指数
    for (int i = 1; i <= cnt_primes; ++i) {
        int p = primes[i];
        int a = 0;
        long long current = p;
        while (current <= N) {
            a += N / current;
            current *= p; // 计算p^2, p^3, ...
        }
        cout << p << " " << a << endl;
    }
    return 0;
}

4.5 两种解法对比

解法	时间复杂度	适用场景	优点	缺点
试除法累加	O(N√N)	N≤1e4	代码简单，无需预处理	效率较低，不适合大数据
线性筛 + 公式	O(N log N)	N≤1e6	效率极高，适合大数据	需要预处理，代码稍复杂

对于题目中 N≤1e4 的限制，两种解法都能通过，但线性筛 + 公式的优势在 N 较大时会更加明显。

五、实战例题 2：洛谷 P10495 阶乘分解（强化版）

题目链接：https://www.luogu.com.cn/problem/P10495

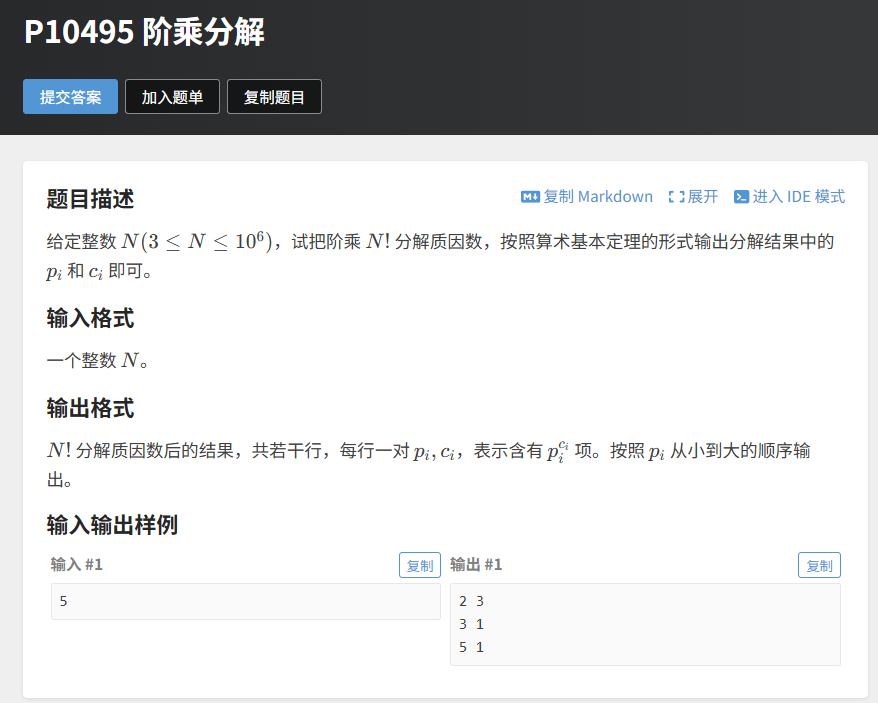
5.1 题目分析

题目描述：给定整数 N（3≤N≤1e6），将 N! 分解质因数，按质因数从小到大输出 pi 和 ci（ci 为 pi 的指数）。

输入：一个整数 N。

输出：若干行，每行一对 pi 和 ci。

示例：输入：5输出：2 33 15 1

核心考点：高效处理大规模阶乘分解（N=1e6），考验线性筛和公式的结合应用。

5.2 优化代码实现

#include <iostream>
#include <cstring>
using namespace std;

typedef long long LL;
const int MAXN = 1e6 + 10;
bool st[MAXN];
int primes[MAXN], cnt;

// 线性筛优化版（筛选质数并存储）
void get_primes(int n) {
    memset(st, 0, sizeof st);
    cnt = 0;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) {
            primes[++cnt] = i;
        }
        // 优化：用long long避免i*primes[j]溢出
        for (int j = 1; 1LL * i * primes[j] <= n; ++j) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int N;
    cin >> N;
    get_primes(N);
    
    for (int i = 1; i <= cnt; ++i) {
        int p = primes[i];
        int ci = 0;
        LL current = p;
        while (current <= N) {
            ci += N / current;
            // 防止current溢出（当p=2，N=1e6时，current最大为2^19=524288，不会溢出）
            if (current > N / p) break; // 提前判断，避免current*p溢出
            current *= p;
        }
        cout << p << " " << ci << endl;
    }
    return 0;
}

5.3 关键优化点

1. 溢出防护 ：在计算 current***= p** 时，提前判断current > N / p，如果成立，则 current*p 会超出 N，直接 break，避免溢出；
2. 输入输出优化 ：使用ios::sync_with_stdio(false); **cin.tie(nullptr);**关闭同步，提升大数据量下的输入输出速度；
3. 线性筛效率 ：线性筛的时间复杂度为O (N) ，后续每个质数的指数计算为 O (log_p N)，整体时间复杂度为 O (N log N)，对于 N=1e6 完全可以在 1 秒内完成。

六、算术基本定理的延伸应用

6.1 约数个数定理

由算术基本定理，若 n 的标准分解式为 ，则 n 的约数个数为：

原理：每个质因子 p_i 可以选择 0 到 α_i 个，共 (α_i + 1) 种选择，所有质因子的选择组合即为约数总数。

示例：n=12=2²×3¹，约数个数为 (2+1)×(1+1)=6，分别是 1、2、3、4、6、12。

6.2 约数和定理

n 的所有约数之和为：

原理：将每个质因子的所有可能次幂相加，再将结果相乘，得到所有约数的和。

示例：n=12=2²×3¹，约数和为 (1+2+4)×(1+3)=7×4=28，验证：1+2+3+4+6+12=28。

6.3 最大公约数与最小公倍数

对于两个数 a 和 b，设其标准分解式为：

（缺失的质因子指数视为 0）则：

• 最大公约数 ：
• 最小公倍数 ：

七、常见误区与避坑指南

7.1 数值溢出问题

• 分解质因数时，i*i 可能溢出：使用i <= x / i替代i*i <= x；
• 阶乘分解时，current *= p 可能溢出：使用 long long 存储 current，并提前判断current > N / p。

7.2 边界条件处理

• 分解质因数时，忘记处理最后剩余的 x>1（如 x 是质数时）；
• 阶乘分解时，N=1 或 N=2 的情况（1! 和 2! 的质因子分解需特殊处理，但题目中 N≥3 可忽略）。

7.3 效率优化误区

• 对单个小数分解时，盲目使用线性筛（预处理成本高于直接试除法）；
• 枚举质因子时，未除尽就跳出循环（导致漏记指数）。

---

总结

在实际竞赛中，这些知识点往往会结合其他数论内容（如欧拉函数、同余方程）考查，因此建议多做综合性题目，加深对定理的理解和应用能力。

如果你在学习过程中遇到具体题目无法解决，或者想进一步了解算术基本定理的其他应用（如大质数分解、密码学中的 RSA 算法），可以随时留言交流。后续将持续更新数论进阶内容，敬请关注！