机器学习知识点梳理(回归模型、分类模型、聚类模型、评估方法)

Maxwell_li12026-01-01 12:24

机器学习知识点梳理

• 回归模型：线性回归、决策树、SVM（可以，效果差）

• 分类模型：逻辑回归、决策树、SVM、朴素贝叶斯（只能分类）

• 聚类模型：kmeans（基于原型）、DBSCAN（基于密度）、凝聚层次（基于层次）

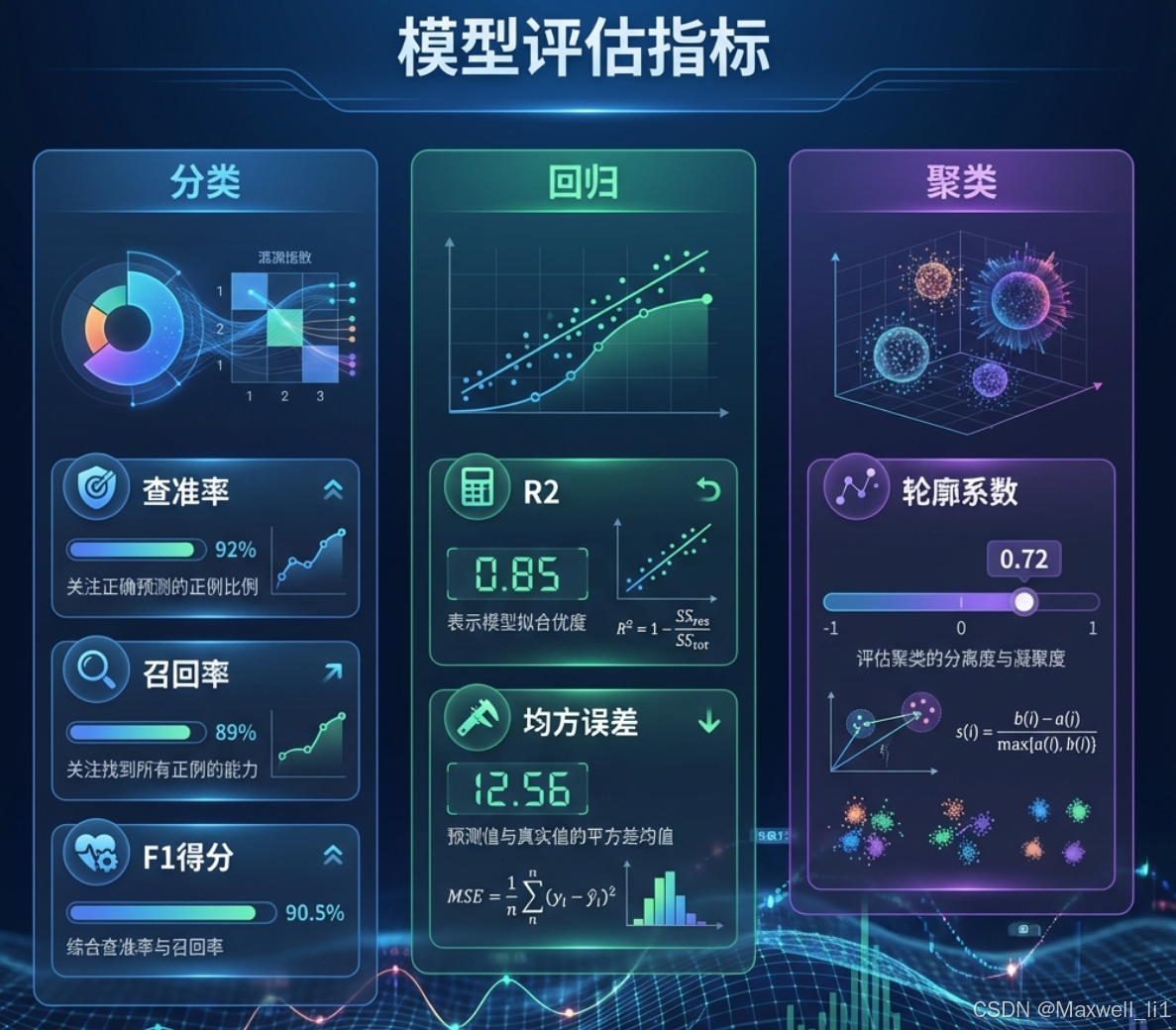
• 评估方法：

◦ 回归问题：R2（综合指标）、均方误差（损失函数）

◦ 分类问题：查准率（评估误检）、召回率（评估漏检）、F1（综合评估前两者）

◦ 聚类问题：轮廓系数


第一部分：常用导入包及其作用

1. 核心科学计算库

python 复制代码 
import numpy as np

作用：NumPy（Numerical Python）是Python科学计算的基础库

  • 提供高性能的多维数组对象（ndarray）
  • 提供数组运算、线性代数、随机数生成等功能
  • 机器学习中用于存储和处理样本数据

2. 数据预处理模块

python 复制代码 
import sklearn.preprocessing as sp

作用：sklearn的预处理模块，提供数据预处理功能

  • sp.scale() - 标准化（均值移除）
  • sp.MinMaxScaler() - 范围缩放
  • sp.normalize() - 归一化
  • sp.Binarizer() - 二值化
  • sp.OneHotEncoder() - 独热编码
  • sp.LabelEncoder() - 标签编码
  • sp.PolynomialFeatures() - 多项式特征扩展

3. 线性模型模块

python 复制代码 
import sklearn.linear_model as lm

作用：sklearn的线性模型模块，提供各种回归算法

  • lm.LinearRegression() - 线性回归
  • lm.Ridge() - 岭回归（L2正则化）
  • lm.Lasso() - Lasso回归（L1正则化）
  • lm.LogisticRegression() - 逻辑回归（分类）

4. 模型评估模块

python 复制代码 
import sklearn.metrics as sm

作用：sklearn的评估模块，提供模型性能评价指标

  • sm.r2_score() - R2决定系数（回归）
  • sm.mean_squared_error() - 均方误差（回归）
  • sm.precision_score() - 查准率（分类）
  • sm.recall_score() - 召回率（分类）
  • sm.f1_score() - F1得分（分类）
  • sm.confusion_matrix() - 混淆矩阵（分类）
  • sm.silhouette_score() - 轮廓系数（聚类）

5. 模型选择模块

python 复制代码 
import sklearn.model_selection as ms

作用：sklearn的模型选择模块，提供数据集划分和交叉验证功能

  • ms.train_test_split() - 划分训练集和测试集
  • ms.cross_val_score() - 交叉验证
  • ms.validation_curve() - 验证曲线
  • ms.learning_curve() - 学习曲线
  • ms.GridSearchCV() - 网格搜索（超参数优化）

6. 支持向量机模块

python 复制代码 
import sklearn.svm as svm

作用：sklearn的支持向量机模块

  • svm.SVC() - 支持向量分类器
  • svm.SVR() - 支持向量回归器

7. 决策树模块

python 复制代码 
import sklearn.tree as st

作用：sklearn的决策树模块

  • st.DecisionTreeRegressor() - 决策树回归器
  • st.DecisionTreeClassifier() - 决策树分类器

8. 朴素贝叶斯模块

python 复制代码 
import sklearn.naive_bayes as nb

作用：sklearn的朴素贝叶斯模块

  • nb.GaussianNB() - 高斯朴素贝叶斯分类器

9. 聚类模块

python 复制代码 
import sklearn.cluster as sc

作用：sklearn的聚类模块

  • sc.KMeans() - K均值聚类
  • sc.DBSCAN() - 噪声密度聚类
  • sc.AgglomerativeClustering() - 凝聚层次聚类

10. 管线模块

python 复制代码 
import sklearn.pipeline as pl

作用：sklearn的管线模块，用于串联多个处理步骤

  • pl.make_pipeline() - 创建处理管线，将预处理和模型串联

11. 集成学习模块

python 复制代码 
import sklearn.ensemble as se

作用：sklearn的集成学习模块

  • se.RandomForestClassifier() - 随机森林分类器
  • se.RandomForestRegressor() - 随机森林回归器

12. 可视化库

python 复制代码 
import matplotlib.pyplot as mp
from mpl_toolkits.mplot3d import axes3d

作用：Matplotlib是Python的绘图库

  • mp.figure() - 创建图形窗口
  • mp.scatter() - 绘制散点图
  • mp.plot() - 绘制折线图
  • mp.show() - 显示图形
  • axes3d - 3D绘图工具

13. 模型持久化

python 复制代码 
import pickle

作用：Python的序列化模块

  • pickle.dump() - 保存模型到文件
  • pickle.load() - 从文件加载模型

第二部分：核心知识点与关键代码

一、回归模型

1. 线性回归（Linear Regression）

名词解释：

  • 线性回归 ：根据样本数据，寻找一个线性模型 y = wx + b，使得预测值与真实值的误差最小
  • 损失函数：度量预测值与真实值差异的函数，常用均方误差（MSE）
  • 梯度下降：通过沿着梯度负方向不断调整参数，使损失函数最小化的优化算法
  • 学习率（η）：梯度下降中参数更新的步长
  • R2决定系数：评估回归模型好坏的指标，值越接近1越好

关键代码：

python 复制代码 
# 1. 使用sklearn实现线性回归
import numpy as np
import sklearn.linear_model as lm
import sklearn.metrics as sm

# 准备数据
train_x = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]])
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0])

# 创建线性回归器
model = lm.LinearRegression()

# 训练模型
model.fit(train_x, train_y)

# 预测
pred_y = model.predict(train_x)

# 评估
r2 = sm.r2_score(train_y, pred_y)
print("R2得分:", r2)
print("系数:", model.coef_)      # 斜率w
print("截距:", model.intercept_)  # 截距b
python 复制代码 
# 2. 多项式回归（处理非线性数据）
import sklearn.pipeline as pl
import sklearn.preprocessing as sp

# 创建多项式回归模型（3次多项式）
model = pl.make_pipeline(
    sp.PolynomialFeatures(3),  # 多项式特征扩展，最高次项为3
    lm.LinearRegression()       # 线性回归器
)

# 训练和预测
model.fit(train_x, train_y)
pred_y = model.predict(train_x)
python 复制代码 
# 3. 岭回归（Ridge）- L2正则化，防止过拟合
model = lm.Ridge(alpha=200,      # 正则化强度
                 max_iter=1000)   # 最大迭代次数
model.fit(train_x, train_y)
pred_y = model.predict(train_x)
python 复制代码 
# 4. Lasso回归 - L1正则化，防止过拟合
model = lm.Lasso(alpha=0.5,      # L1范数系数
                 max_iter=1000)   # 最大迭代次数
model.fit(train_x, train_y)
pred_y = model.predict(train_x)

评估指标：

python 复制代码 
# R2决定系数（值越接近1越好，范围[0,1]）
r2 = sm.r2_score(y_true, y_pred)

# 均方误差（值越小越好）
mse = sm.mean_squared_error(y_true, y_pred)
2. 决策树回归（Decision Tree Regression）

名词解释：

  • 决策树：通过树形结构进行决策的模型，每个节点代表一个特征判断
  • 叶节点：树的终端节点，存储预测值
  • max_depth：树的最大深度，控制模型复杂度

关键代码：

python 复制代码 
import sklearn.tree as st

# 创建决策树回归器
model = st.DecisionTreeRegressor(max_depth=4)  # 最大深度为4

# 训练
model.fit(train_x, train_y)

# 预测
pred_y = model.predict(test_x)

# 评估
r2 = sm.r2_score(test_y, pred_y)
3. SVM回归（效果较差，不推荐）
python 复制代码 
import sklearn.svm as svm

# 创建SVM回归器
model = svm.SVR(kernel='rbf',    # 核函数
                C=1.0,            # 惩罚参数
                gamma='auto')     # 核系数

model.fit(train_x, train_y)
pred_y = model.predict(test_x)

二、分类模型

1. 逻辑回归（Logistic Regression）

名词解释：

  • 逻辑回归：虽然名为"回归"，但实际是分类算法，通过Sigmoid函数将线性回归结果映射到[0,1]区间
  • Sigmoid函数：S型曲线函数，用于二分类概率计算

关键代码：

python 复制代码 
import sklearn.linear_model as lm

# 创建逻辑回归分类器
model = lm.LogisticRegression(
    solver='liblinear',  # 优化算法
    C=1.0                # 正则化强度的倒数
)

# 训练
model.fit(train_x, train_y)

# 预测
pred_y = model.predict(test_x)

# 预测概率
pred_proba = model.predict_proba(test_x)
2. 决策树分类（Decision Tree Classification）

关键代码：

python 复制代码 
import sklearn.tree as st

# 创建决策树分类器
model = st.DecisionTreeClassifier(
    max_depth=4,           # 最大深度
    criterion='entropy'    # 划分标准：'entropy'(信息熵) 或 'gini'(基尼系数)
)

# 训练
model.fit(train_x, train_y)

# 预测
pred_y = model.predict(test_x)
3. 支持向量机（SVM）

名词解释：

  • SVM：寻找最优超平面来划分不同类别的样本
  • 核函数：将低维空间映射到高维空间，使线性不可分问题变得可分
  • C参数：惩罚参数，控制对误分类的容忍度
  • gamma参数：核函数系数，影响决策边界的复杂度

关键代码：

python 复制代码 
import sklearn.svm as svm

# 1. 线性核SVM
model = svm.SVC(kernel='linear', C=1.0)

# 2. 多项式核SVM
model = svm.SVC(kernel='poly', 
                degree=3,  # 多项式次数
                C=1.0)

# 3. 径向基核（RBF）SVM - 最常用
model = svm.SVC(kernel='rbf', 
                C=1.0, 
                gamma='auto')

# 训练和预测
model.fit(train_x, train_y)
pred_y = model.predict(test_x)
4. 朴素贝叶斯（Naive Bayes）- 只能分类

名词解释：

  • 朴素贝叶斯：基于贝叶斯定理和特征独立性假设的分类算法
  • 先验概率：事件发生前的概率
  • 后验概率：事件发生后的概率
  • 高斯朴素贝叶斯：假设特征服从高斯（正态）分布

关键代码：

python 复制代码 
import sklearn.naive_bayes as nb

# 创建高斯朴素贝叶斯分类器
model = nb.GaussianNB()

# 训练
model.fit(train_x, train_y)

# 预测
pred_y = model.predict(test_x)

三、分类问题评估指标

名词解释：

  • 查准率（Precision）：预测为正例中真正为正例的比例，评估误检情况

    • 公式：TP / (TP + FP)
    • 关注：预测的准不准

  • 召回率（Recall）：真正为正例中被预测为正例的比例，评估漏检情况

    • 公式：TP / (TP + FN)
    • 关注：找得全不全

  • F1得分：查准率和召回率的调和平均，综合评估

    • 公式：2 * (Precision * Recall) / (Precision + Recall)

  • 混淆矩阵：展示分类结果的矩阵，行表示真实类别，列表示预测类别

关键代码：

python 复制代码 
import sklearn.metrics as sm
import sklearn.model_selection as ms

# 1. 划分训练集和测试集
train_x, test_x, train_y, test_y = ms.train_test_split(
    x, y, 
    test_size=0.25,    # 测试集占25%
    random_state=7     # 随机种子
)

# 2. 计算查准率
precision = sm.precision_score(
    test_y, pred_y,
    average='macro'    # 多分类：'macro', 'micro', 'weighted'
)

# 3. 计算召回率
recall = sm.recall_score(
    test_y, pred_y,
    average='macro'
)

# 4. 计算F1得分
f1 = sm.f1_score(
    test_y, pred_y,
    average='macro'
)

# 5. 混淆矩阵
cm = sm.confusion_matrix(test_y, pred_y)
print("混淆矩阵:\n", cm)

# 6. 准确率（Accuracy）
accuracy = sm.accuracy_score(test_y, pred_y)

交叉验证评估：

python 复制代码 
# 交叉验证（5折）
precision_scores = ms.cross_val_score(
    model, x, y,
    cv=5,                        # 5折交叉验证
    scoring='precision_weighted' # 查准率
)

recall_scores = ms.cross_val_score(
    model, x, y, 
    cv=5,
    scoring='recall_weighted'    # 召回率
)

f1_scores = ms.cross_val_score(
    model, x, y,
    cv=5,
    scoring='f1_weighted'        # F1得分
)

print("查准率:", precision_scores.mean())
print("召回率:", recall_scores.mean())
print("F1得分:", f1_scores.mean())

四、聚类模型

名词解释：

  • 聚类：无监督学习，将相似的样本划分到同一簇中
  • 欧式距离：计算样本间相似度的常用方法
  • 簇（Cluster）：聚类后的群落
1. K-Means（基于原型聚类）

名词解释：

  • K-Means：根据事先给定的聚类数K，随机选择K个中心点，迭代优化
  • 聚类中心：每个簇的几何中心
  • n_clusters：聚类数量，需要事先指定

特点：

  • 优点：简单高效，收敛快
  • 缺点：需要事先知道K值，对初始中心敏感，对噪声敏感
  • 适用：数据有明显中心，聚类数量已知

关键代码：

python 复制代码 
import sklearn.cluster as sc
import sklearn.metrics as sm

# 创建K-Means聚类器
model = sc.KMeans(n_clusters=4)  # 聚类数量为4

# 训练
model.fit(x)

# 获取聚类结果
pred_y = model.labels_            # 每个样本的聚类标签
centers = model.cluster_centers_  # 聚类中心坐标

# 评估：计算轮廓系数
score = sm.silhouette_score(
    x, pred_y,
    sample_size=len(x),
    metric='euclidean'  # 欧式距离
)
print("轮廓系数:", score)
2. DBSCAN（基于密度聚类）

名词解释：

  • DBSCAN：基于密度的聚类算法，不需要事先指定聚类数
  • 邻域半径（eps）：定义样本邻域的范围
  • 最小样本数（min_samples）：核心点邻域内的最小样本数
  • 核心点：邻域内样本数 >= min_samples的点
  • 边界点：可归入某簇但无法扩展新样本的点
  • 噪声点：无法归入任何簇的点（标签为-1）

特点：

  • 优点：不需要指定K值，能处理噪声，能识别任意形状的簇
  • 缺点：对参数敏感，密度不均时效果差
  • 适用：数据稠密无明显中心，噪声较多，未知聚类数

关键代码：

python 复制代码 
import sklearn.cluster as sc

# 创建DBSCAN聚类器
model = sc.DBSCAN(
    eps=0.8,           # 邻域半径
    min_samples=5      # 最小样本数
)

# 训练
model.fit(x)

# 获取聚类结果
pred_y = model.labels_                    # 聚类标签（-1表示噪声点）
core_indices = model.core_sample_indices_ # 核心样本的索引

# 区分不同类型的点
core_mask = np.zeros(len(x), dtype=bool)
core_mask[core_indices] = True     # 核心点
noise_mask = (pred_y == -1)        # 噪声点
periphery_mask = ~(core_mask | noise_mask)  # 边界点
3. 凝聚层次聚类（基于层次）

名词解释：

  • 凝聚层次聚类：自底向上，初始每个样本为一簇，逐步合并最近的簇
  • linkage ：簇间距离计算方式
    • ward：方差最小化（默认）
    • average：平均距离
    • complete：最大距离

特点：

  • 优点：无需初始中心，对中心不明显的数据效果好
  • 缺点：需要事先指定聚类数，无法进行预测
  • 适用：中心特征不明显的聚类

关键代码：

python 复制代码 
import sklearn.cluster as sc

# 创建凝聚层次聚类器
model = sc.AgglomerativeClustering(
    n_clusters=4,     # 聚类数量
    linkage='ward'    # 链接方式
)

# 训练
model.fit(x)

# 获取聚类结果
pred_y = model.labels_

五、聚类评估指标

名词解释：

  • 轮廓系数（Silhouette Score） ：评估聚类质量的指标
    • 范围：[-1, 1]
    • 值越接近1，聚类效果越好（内密外疏）
    • 值接近-1，聚类效果差
    • 值接近0，聚类有重叠

关键代码：

python 复制代码 
import sklearn.metrics as sm

# 计算轮廓系数
score = sm.silhouette_score(
    x,                    # 样本数据
    pred_y,              # 聚类标签
    sample_size=len(x),  # 样本数量
    metric='euclidean'   # 距离度量方式
)

print("轮廓系数:", score)

六、数据预处理

1. 标准化（均值移除）

名词解释：

  • 标准化：使数据均值为0，标准差为1
  • 用途：消除量纲影响，提高模型训练效果
python 复制代码 
import sklearn.preprocessing as sp

# 方法1：直接标准化
std_data = sp.scale(raw_data)

# 方法2：创建标准化器
scaler = sp.StandardScaler()
std_data = scaler.fit_transform(raw_data)
2. 范围缩放

名词解释：

  • 范围缩放：将特征值缩放到指定范围（通常[0,1]）
python 复制代码 
# 创建范围缩放器
mms = sp.MinMaxScaler(feature_range=(0, 1))
scaled_data = mms.fit_transform(raw_data)
3. 归一化

名词解释：

  • 归一化：每个样本的特征值除以该样本所有特征值的和（或范数）
python 复制代码 
# L1归一化
nor_data = sp.normalize(raw_data, norm='l1')

# L2归一化
nor_data = sp.normalize(raw_data, norm='l2')
4. 独热编码

名词解释：

  • 独热编码：将分类特征转换为二进制向量，可逆编码
python 复制代码 
# 创建独热编码器
encoder = sp.OneHotEncoder(
    sparse=False,      # 不使用稀疏矩阵
    dtype='int32'
)

# 编码
encoded_data = encoder.fit_transform(raw_data)

# 解码
decoded_data = encoder.inverse_transform(encoded_data)
5. 标签编码

名词解释：

  • 标签编码：将字符串标签转换为数字标签
python 复制代码 
# 创建标签编码器
encoder = sp.LabelEncoder()

# 编码
encoded_labels = encoder.fit_transform(labels)

# 解码
decoded_labels = encoder.inverse_transform(encoded_labels)

七、模型优化

1. 网格搜索（超参数优化）

名词解释：

  • 超参数：模型训练前需要设置的参数（如树深度、学习率等）
  • 网格搜索：穷举所有参数组合，找到最优参数
python 复制代码 
import sklearn.model_selection as ms
import sklearn.svm as svm

# 定义参数网格
params = [
    {'kernel': ['linear'], 'C': [1, 10, 100, 1000]},
    {'kernel': ['poly'], 'C': [1], 'degree': [2, 3]},
    {'kernel': ['rbf'], 'C': [1, 10, 100], 'gamma': [1, 0.1, 0.01]}
]

# 创建网格搜索对象
model = ms.GridSearchCV(
    svm.SVC(),      # 基础模型
    params,         # 参数网格
    cv=5            # 5折交叉验证
)

# 训练
model.fit(x, y)

# 获取最优参数和最优得分
print("最优得分:", model.best_score_)
print("最优参数:", model.best_params_)
2. 验证曲线

名词解释：

  • 验证曲线：评估不同超参数值对模型性能的影响
python 复制代码 
import sklearn.model_selection as ms

# 定义参数范围
param_range = np.arange(50, 550, 50)

# 获取验证曲线
train_scores, test_scores = ms.validation_curve(
    model,              # 模型
    x, y,               # 数据
    'n_estimators',     # 参数名
    param_range,        # 参数值范围
    cv=5                # 交叉验证折数
)

# 计算平均得分
train_mean = train_scores.mean(axis=1)
test_mean = test_scores.mean(axis=1)
3. 学习曲线

名词解释：

  • 学习曲线：评估不同训练集大小对模型性能的影响
python 复制代码 
import sklearn.model_selection as ms

# 定义训练集大小范围
train_sizes = np.linspace(0.1, 1.0, 10)

# 获取学习曲线
train_sizes, train_scores, test_scores = ms.learning_curve(
    model,           # 模型
    x, y,            # 数据
    train_sizes=train_sizes,  # 训练集大小
    cv=5             # 交叉验证
)

train_mean = train_scores.mean(axis=1)
test_mean = test_scores.mean(axis=1)

八、模型保存与加载

python 复制代码 
import pickle

# 保存模型
with open('model.pkl', 'wb') as f:
    pickle.dump(model, f)
    print("模型保存成功")

# 加载模型
with open('model.pkl', 'rb') as f:
    model = pickle.load(f)
    print("模型加载成功")

# 使用加载的模型预测
pred_y = model.predict(test_x)

第三部分：完整示例代码

示例1：线性回归完整流程

python 复制代码 
import numpy as np
import sklearn.linear_model as lm
import sklearn.metrics as sm
import sklearn.model_selection as ms
import matplotlib.pyplot as mp

# 1. 读取数据
x, y = [], []
with open("data.txt", "r") as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(",")]
        x.append(data[:-1])
        y.append(data[-1])

x = np.array(x)
y = np.array(y)

# 2. 划分训练集和测试集
train_x, test_x, train_y, test_y = ms.train_test_split(
    x, y, test_size=0.25, random_state=7
)

# 3. 创建并训练模型
model = lm.LinearRegression()
model.fit(train_x, train_y)

# 4. 预测
pred_y = model.predict(test_x)

# 5. 评估
r2 = sm.r2_score(test_y, pred_y)
print("R2得分:", r2)

# 6. 可视化
mp.figure('Linear Regression', facecolor='lightgray')
mp.scatter(test_x, test_y, c='blue', label='真实值')
mp.plot(test_x, pred_y, c='red', label='预测值')
mp.legend()
mp.show()

示例2：分类问题完整流程

python 复制代码 
import numpy as np
import sklearn.model_selection as ms
import sklearn.metrics as sm
import sklearn.naive_bayes as nb

# 1. 读取数据
x, y = [], []
with open("data.txt", "r") as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(",")]
        x.append(data[:-1])
        y.append(data[-1])

x = np.array(x)
y = np.array(y, dtype=int)

# 2. 划分训练集和测试集
train_x, test_x, train_y, test_y = ms.train_test_split(
    x, y, test_size=0.25, random_state=7
)

# 3. 创建并训练模型
model = nb.GaussianNB()
model.fit(train_x, train_y)

# 4. 预测
pred_y = model.predict(test_x)

# 5. 评估
print("查准率:", sm.precision_score(test_y, pred_y, average='macro'))
print("召回率:", sm.recall_score(test_y, pred_y, average='macro'))
print("F1得分:", sm.f1_score(test_y, pred_y, average='macro'))
print("混淆矩阵:\n", sm.confusion_matrix(test_y, pred_y))

示例3：聚类问题完整流程

python 复制代码 
import numpy as np
import sklearn.cluster as sc
import sklearn.metrics as sm
import matplotlib.pyplot as mp

# 1. 读取数据
x = []
with open("data.txt", "r") as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(",")]
        x.append(data)

x = np.array(x)

# 2. 创建并训练K-Means模型
model = sc.KMeans(n_clusters=4)
model.fit(x)

# 3. 获取结果
pred_y = model.labels_
centers = model.cluster_centers_

# 4. 评估
score = sm.silhouette_score(x, pred_y, metric='euclidean')
print("轮廓系数:", score)

# 5. 可视化
mp.figure('K-Means', facecolor='lightgray')
mp.scatter(x[:, 0], x[:, 1], c=pred_y, cmap='brg')
mp.scatter(centers[:, 0], centers[:, 1], 
           marker='+', c='black', s=200)
mp.show()
相关推荐
咚咚王者2 小时前
人工智能之核心基础 机器学习 第三章 线性回归与逻辑回归
人工智能·机器学习·线性回归
540_5403 小时前
ADVANCE Day31
人工智能·python·机器学习
深度学习实战训练营3 小时前
结合 Swin Transformer 与 LSTM 的残差自回归模型，用于高精度光学波前时序预测与相位重建
回归·lstm·transformer
yuhaiqun19893 小时前
发现前端性能瓶颈的巧妙方法：建立“现象归因→分析定位→优化验证”的闭环思维
前端·经验分享·笔记·python·学习·课程设计·学习方法
Das13 小时前
【机器学习】02_线性模型
人工智能·机器学习
yongui478343 小时前
基于BP_Adaboost的分类器和RBF神经网络回归的实现方法
人工智能·神经网络·回归
adjust25864 小时前
day 46
人工智能·机器学习·numpy
兜兜转转了多少年4 小时前
《Python 应用机器学习：代码实战指南》笔记2 从0理解机器学习 —— 核心概念全解析
笔记·python·机器学习
生信碱移5 小时前
神经网络单细胞预后分析：这个方法直接把 TCGA 预后模型那一套迁移到单细胞与空转数据上了！竟然还能做模拟敲除与预后靶点筛选？！
人工智能·深度学习·神经网络·算法·机器学习·数据挖掘·数据分析
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03jdk21下载、安装（Windows、Linux、macOS）04Claude Code Skills 实用使用手册05从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击06UV安装并设置国内源072025 最新教程：注册并切换到美区 Apple ID08【踩坑笔记】50系显卡适配的 PyTorch 安装09祝大家 2026 年新年快乐，代码无 bug，需求一次过10Google Antigravity Agent 编辑器操作教程