1 静态查找表
2 二叉排序树的查找
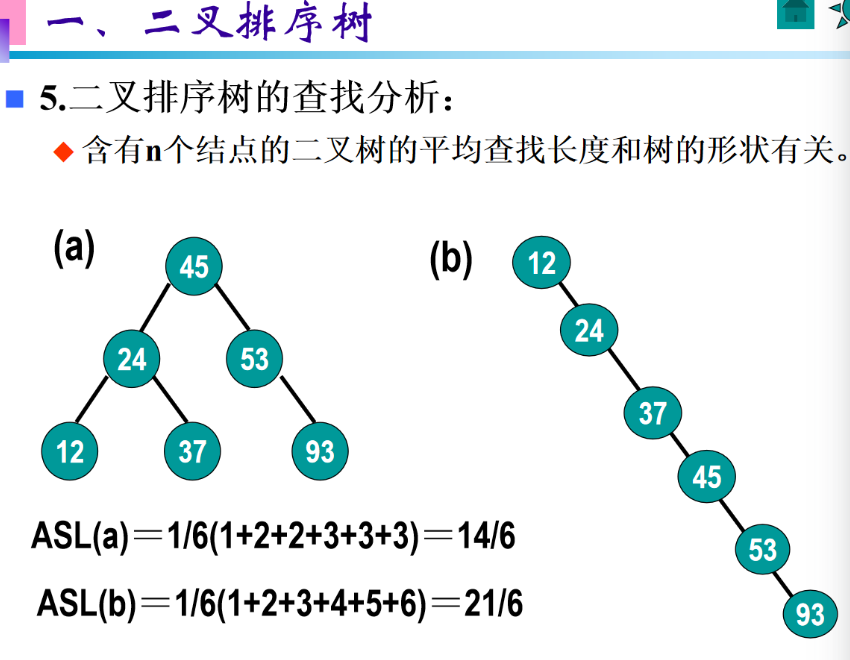

二叉排序树的平均查找长度(ASL)计算方法是:所有结点的查找长度之和,除以结点总数n。
具体步骤:
- 确定每个结点的查找长度:结点的查找长度 = 从根结点到该结点的路径长度(路径上的边数) + 1(根结点自身的查找长度为 1)。
- 求和并求平均:将所有结点的查找长度相加,再除以结点数n,得到 ASL。
以图中例子说明:
-
图 (a) 的二叉排序树(共 6 个结点):
- 根结点 45:查找长度 = 1
- 结点 24、53:查找长度 = 2
- 结点 12、37、93:查找长度 = 3
- 求和:1 + 2 + 2 + 3 + 3 + 3 = 14
- ASL(a) = 14/6
-
图 (b) 的二叉排序树(共 6 个结点,退化为单链表):
- 结点 12(根):查找长度 = 1
- 结点 24:查找长度 = 2
- 结点 37:查找长度 = 3
- 结点 45:查找长度 = 4
- 结点 53:查找长度 = 5
- 结点 93:查找长度 = 6
- 求和:1+2+3+4+5+6 = 21
- ASL(b) = 21/6
3 AVL 树的 4 种旋转

区分 AVL 树的 4 种旋转,核心是先找"失衡的最小子树",再看新结点插入的位置,对应不同旋转类型:
第一步:先找 "失衡的最小子树"
AVL 树失衡的标志是:某个结点的左右子树高度差的绝对值 > 1 。
我们需要找到最靠近新插入结点的失衡结点(这是 "最小失衡子树" 的根)。
第二步:根据新结点的插入位置,对应旋转类型
以 "最小失衡子树的根" 为基准,看新结点插入在它的左子树的左子树(LL)、左子树的右子树(LR)、右子树的右子树(RR)、右子树的左子树(RL),对应 4 种旋转:
1. LL 旋转(单向右旋)
- 场景:新结点插入到 "失衡根的左子树的左子树"。
- 操作:把失衡根的左孩子作为新根,失衡根作为新根的右孩子,原左孩子的右子树挂到失衡根的左子树。
- 例子:
失衡根是 A,左孩子是 B,新结点插在 B 的左子树 → 右旋后 B 成为新根,A 是 B 的右孩子,B 原来的右子树变 A 的左子树。
2. RR 旋转(单向左旋)
- 场景:新结点插入到 "失衡根的右子树的右子树"。
- 操作:把失衡根的右孩子作为新根,失衡根作为新根的左孩子,原右孩子的左子树挂到失衡根的右子树。
- 例子:
失衡根是 A,右孩子是 B,新结点插在 B 的右子树 → 左旋后 B 成为新根,A 是 B 的左孩子,B 原来的左子树变 A 的右子树。
3. LR 旋转(先左旋再右旋)
- 场景:新结点插入到 "失衡根的左子树的右子树"。
- 操作:先对失衡根的左孩子做 RR 旋转(左旋),再对失衡根本身做 LL 旋转(右旋)。
- 例子:
失衡根是 A,左孩子是 B,新结点插在 B 的右子树 → 先把 B 左旋(让 B 的右孩子 C 成为 B 的父结点),再把 A 右旋(让 C 成为新根)。
4. RL 旋转(先右旋再左旋)
- 场景:新结点插入到 "失衡根的右子树的左子树"。
- 操作:先对失衡根的右孩子做 LL 旋转(右旋),再对失衡根本身做 RR 旋转(左旋)。
- 例子:
失衡根是 A,右孩子是 B,新结点插在 B 的左子树 → 先把 B 右旋(让 B 的左孩子 C 成为 B 的父结点),再把 A 左旋(让 C 成为新根)。
简单总结:
- 单旋(LL/RR):新结点插在 "左左" 或 "右右",直接旋一次;
- 双旋(LR/RL):新结点插在 "左右" 或 "右左",先旋孩子,再旋根。
理解"左旋""右旋"
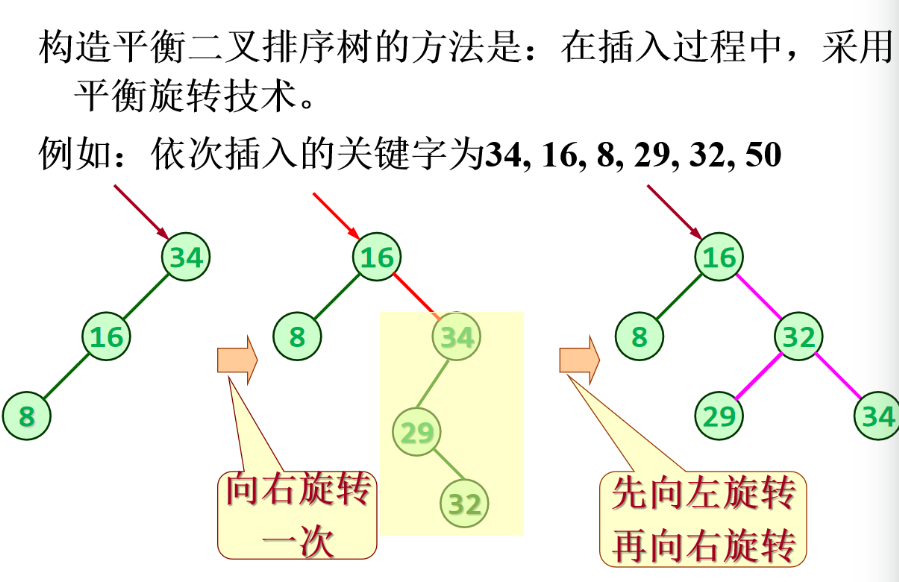
要理解平衡二叉树的向右旋转(右旋),可以把树想象成 "绕某个节点转动" 的过程,我用这个例子拆解:
第一步:初始状态(插入 34、16、8 后的树)
此时树的结构是:
34
/
16
/
8这是LL 型不平衡 (34 的左孩子的左子树过重),需要对34 进行右旋。
右旋的过程(绕 34 旋转)
右旋的核心是:把 "左孩子(16)" 提升为新的根,原根(34)变成左孩子的右孩子,步骤如下:
- 原根是
34,它的左孩子是16; - 把
16提升为新的根节点; - 原根
34,变成16的右孩子; - 原来
16的右子树(这里为空),变成34的左子树。
旋转后结构就变成:
16
/ \
8 34(这就是你图中 "向右旋转一次" 后的结果 ------16 成为根,34 在它的右侧)
为什么你觉得是 "34 向左转"?
其实右旋是绕原根(34)向右转动,从视觉上看:原根 34 从 "上方" 转到了 "右下方",相当于 34 "向左摆动",但操作的定义是 "对 34 做右旋"(因为是基于原根的左子树过重,通过右旋来平衡)。
后续的 "先左旋再右旋"(插入 29、32 后)
插入 29、32 后,16 的右子树(34)出现了LR 型不平衡(34 的左孩子的右子树过重),所以要:
- 先对
34做左旋(把 29 提升为 34 的父节点); - 再对
16做右旋(把 32 提升为新的根),最终得到图中右侧的结构。
我还是没理解这个词
那我们换个更通俗的方式,用 "父子位置交换" 来理解旋转:
先明确:旋转的 "核心对象"
旋转是针对 "不平衡的节点" 和它的 "子节点"做的操作。比如 "对节点 A 右旋",就是让 A 和它的左孩子 B 交换位置(同时调整子树)。
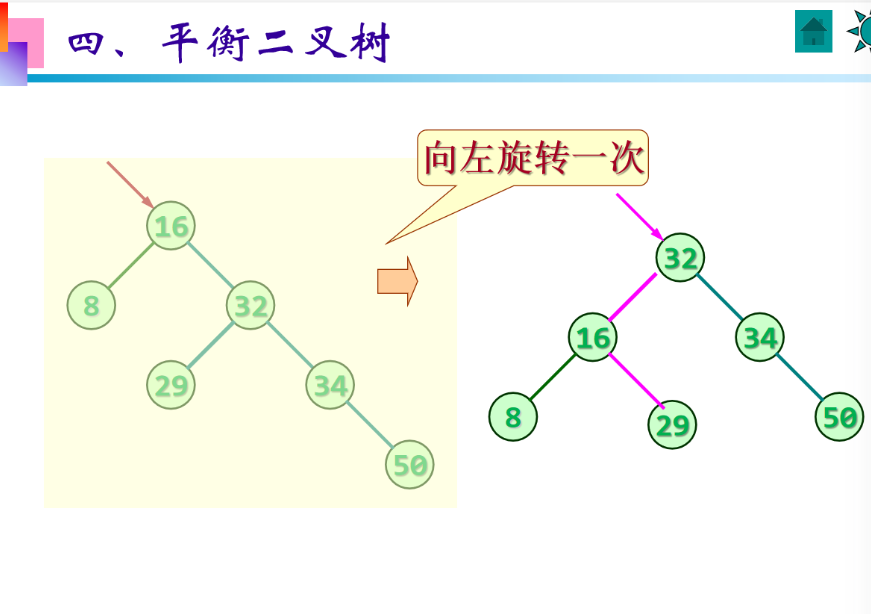
用你的例子拆解 "右旋(对 34 右旋)"
初始结构(34 是根):
爸爸(34)
/
儿子(16)
/
孙子(8)右旋的动作 :
把 "儿子(16)" 升级成新爸爸,原爸爸(34)变成 "儿子的右儿子":
- 原儿子(16)当新根(新爸爸);
- 原爸爸(34),变成新爸爸(16)的右孩子;
- 原儿子(16)原本的右子树(这里是空),变成原爸爸(34)的左子树。
旋转后结构:
新爸爸(16)
/ \
孙子(8) 原爸爸(34)为啥叫 "右旋"?
你可以把树想象成 "固定在原爸爸(34)上的杆子":
- 原儿子(16)在 34 的左边,把杆子向右掰,16 就转到了 34 的上方(变成新根),34 则落到 16 的右边 ------ 这个动作叫 "右旋"。
再总结:
- 右旋 :针对 "某节点的左子树过重",让该节点和它的左孩子交换位置(左孩子变新根,原节点变右孩子)。
- 左旋 :针对 "某节点的右子树过重",让该节点和它的右孩子交换位置(右孩子变新根,原节点变左孩子)。
4 小结
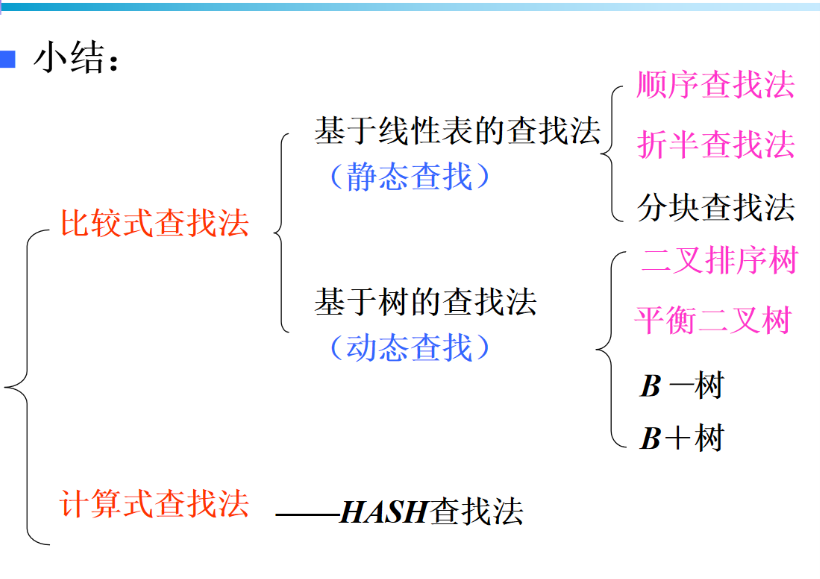
一、先分大类:比较式 vs 计算式
- 比较式查找:靠 "和数据比较" 找目标(比如查字典挨个翻)
- 计算式查找(HASH):靠 "计算地址" 直接找(比如用学号算宿舍号)
二、逐个拆解核心考点
1. 基于线性表的查找(静态:数据不增删)
- 顺序查找 :
- 啥样:挨个遍历(比如从数组第 1 个查到最后 1 个)
- 考法:算平均查找长度(成功 / 失败的次数)
- 折半查找 :
- 啥样:必须是有序表,每次取中间值缩小范围(比如查字典先翻中间,再判断前后)
- 考法:画折半查找判定树、算平均查找长度
- 分块查找 :
- 啥样:把表分成几块(块内无序、块间有序),先查 "块索引" 找块,再在块内顺序查
- 考法:算平均查找长度(索引查找 + 块内查找)
2. 基于树的查找(动态:数据可增删)
- 二叉排序树 :
- 啥样:左子树 < 根 < 右子树,插入 / 删除后保持这个规则
- 考法:构建二叉排序树、找查找路径
- 平衡二叉树(AVL) :
- 啥样:二叉排序树 + 任意节点左右子树高度差≤1,不平衡就旋转(LL/LR/RR/RL)
- 考法:插入节点后判断不平衡类型、做旋转调整
- B - 树 / B + 树 :
- 啥样:多叉树(用于磁盘等外存),B - 树是 "节点存数据 + 索引",B + 树是 "叶子节点存数据,非叶子存索引"
- 考法:B - 树的插入 / 删除(分裂 / 合并节点)、B 和 B + 的区别
3. HASH 查找(计算式)
- 啥样:用哈希函数算 "关键字→地址",冲突了用开放定址 / 链地址解决
- 考法:构造哈希表、算平均查找长度