前言：当AlphaGo击败李世石的那一刻，强化学习这个原本藏在学术殿堂里的概念，第一次以震撼的姿态走进了大众视野。它所展现的"智能体通过与环境互动、从试错中学习最优策略"的核心逻辑，不仅颠覆了人们对"学习"的传统认知，更勾勒出了人工智能走向自主决策的重要路径。从游戏AI的精准操作，到机器人的自主导航，再到金融领域的智能风控、工业场景的优化调度，强化学习正以强大的泛化能力，在各个行业掀起变革浪潮。本人也是心血来潮想要对强化学习学习一二，若有错误之处，请大家指正。
一、常见符号和专有名词
| 符号 | 中文名称 | 英文名称 | 核心解释 | |
|---|---|---|---|---|
| S或s | 状态 | state | 智能体所处的环境情况，是环境的描述 | |
| A或a | 动作 | action | 智能体在当前状态下可执行的操作 | |
| R或r | 奖励 | reward | 智能体执行动作后，环境给出的即时反馈（正 / 负向） | |
| U或u | 回报 | return | 从当前时刻开始，智能体获得的所有奖励的（折扣）总和 | |
| γ | 折扣率 | discount factor | 给未来奖励 "打折" 的系数（0<γ≤1），体现对未来奖励的重视程度 | |
| 状态空间 | state space | 所有可能状态的集合 | ||
| 动作空间 | action space | 所有可能动作的集合 | ||
| π(a|s) | 随机策略函数 | stochastic policy function | 状态s下，智能体选择动作a的概率分布 | |
| μ(s) | 确定策略函数 | deterministic policy function | 状态s下，智能体确定选择的动作（无随机性） | |
| p(s′|s,a) | 状态转移函数 | state-transition function | 状态s执行动作a后，转移到新状态s′的概率 | |
| Qπ(s,a) | 动作价值函数 | action-value function | 策略π下，状态s执行动作a后的期望回报 | |
| Q∗(s,a) | 最优动作价值函数 | optimal action-value function | 所有策略中，状态s执行动作a的最大期望回报 | |
| Vπ(s) | 状态价值函数 | state-value function | 策略π下，状态s的期望回报（策略选动作的平均价值） | |
| V∗(s) | 最优状态价值函数 | optimal state-value function | 所有策略中，状态s的最大期望回报 | |
| Dπ(s) | 优势函数 | advantage function | 动作价值与状态价值的差值，体现动作相对当前策略的 "优势" | |
| D∗(s) | 最优优势函数 | optimal advantage function | 最优策略下的优势函数 | |
| π(a|s;θ) | 随机策略网络 | stochastic policy network | 用神经网络（参数θ）表示的随机策略函数 | |
| μ(s;θ) | 确定策略网络 | deterministic policy network | 用神经网络（参数θ）表示的确定策略函数 | |
| Q(s,a;w) | 深度 Q 网络 | deep Q network (DQN) | 用神经网络（参数w）表示的动作价值函数（解决高维状态问题） | |
| q(s,a;w) | 价值网络 | value network | 用神经网络（参数w）表示的价值函数（动作 / 状态价值） |
二、概率论基础与蒙特卡洛采样
2.1 概率论基础
（1）随机变量
定义 ：随机变量是一个将随机试验的结果 映射为实数的函数，通常用大写字母 X,Y,Z 表示。它的核心作用是将随机试验中不确定的、非数值的结果（如抛硬币的 "正面""反面"）转化为可计算的数值（如 X=1 代表正面，X=0 代表反面）。
分类：
- 离散型随机变量：取值为有限个或可列无限个（如骰子点数 {1,2,3,4,5,6}、某网站日访问量）。
- 连续型随机变量：取值为一个或多个区间内的所有实数（如人的身高、零件的测量误差）。
（2）观测值
定义 ：随机变量的一次具体取值，称为观测值，通常用小写字母 x,y,z 表示。
- 例：抛硬币 10 次，定义 X 为正面次数，X 是随机变量；某次试验得到正面 6 次，x=6 就是 X 的一个观测值。
- 观测值是确定的数值 ，随机变量是不确定的变量。
（3）概率质量函数（PMF）
定义 ：仅适用于离散型随机变量 ，描述随机变量取某个特定值的概率，记为 或 P(x)。满足两个条件：
≥0,∀x
- 例：抛均匀硬币，X=1（正面），X=0（反面），PMF 为
（4）概率密度函数（PDF）
定义 ：仅适用于连续型随机变量，描述随机变量在某个取值区间内的概率 "密集程度"，记为 fX(x) 或 f(x)。满足两个条件：
关键性质：
-
连续型随机变量取单个值的概率为 0，即 P(X=a)=0。
-
概率需通过区间积分 计算：
-
例：均匀分布 X∼U(a,b) 的 PDF 为
2. 期望（Expectation）
期望是随机变量的加权平均值，反映随机变量取值的 "中心趋势"，记为 E[X] 或 μ。
（1）离散型随机变量的期望
- 条件：
（2）连续型随机变量的期望
- 条件：
（3）期望的核心性质
- 线性性：
- 若 X,Y 独立，则
3. 二维及以上随机变量的期望求解
（1）二维随机变量的联合分布
- 离散型 ：联合概率质量函数
- 连续型 ：联合概率密度函数
（2）二维随机变量的期望
① 单个随机变量的期望（边际期望）
-
离散型
-
其中
-
连续型
其中
② 函数的期望
这是更通用的形式，g(X,Y) 是 X,Y 的二元函数（如 XY,X+Y）。
-
离散型
-
连续型
-
例：求 E[X+Y]（连续型）
这验证了期望的线性性。
（3）多维随机变量（n 维）的期望
对于 n 维随机变量 ，联合 PDF 为 f(x1,x2,...,xn)，则
- 单个变量的期望
- 函数的期望
2.2 蒙特卡洛
蒙特卡洛采样是一种基于随机抽样的数值计算方法，核心思想是：通过生成大量随机样本，利用样本的统计特性（均值、方差等）来近似求解确定性问题（如积分、期望、复杂函数值）。
它的优势在于不依赖问题的解析性质 ，即使问题没有闭式解，只要能生成样本，就能通过统计模拟得到近似结果；缺点是精度依赖样本数量，样本越多，结果越准确，但计算成本也越高。
案例 1：近似圆周率 π
这个例子是蒙特卡洛方法的经典入门场景，完全靠随机投点实现。
在一个边长为 2 的正方形里（中心在原点，范围 [-1,1]×[-1,1]），画一个半径为 1 的内切圆。
- 往正方形里随机扔很多点，点落在圆内的概率 = 圆的面积 ÷ 正方形的面积
- 统计圆内的点数占总点数的比例，就能反推出 π 的值
步骤
- 生成
n个随机点，每个点的横坐标x和纵坐标y都在-1到1之间。 - 对每个点判断：如果
x² + y² ≤ 1，说明这个点在圆内。 - 统计圆内的点数
m，用4 × m/n作为 π 的近似值（4 是正方形面积和圆面积的比例系数）。
案例 2：近似复杂积分
很多积分没有现成的计算公式，蒙特卡洛采样可以轻松解决，尤其适合高维积分。
比如要计算 ∫₀¹ e^(-x²)dx 这个积分，我们可以：
- 在
0到1之间随机生成大量x值。 - 对每个
x计算对应的函数值e^(-x²)。 - 把所有函数值取平均值，再乘以区间长度
1（因为积分区间是 0 到 1），结果就是积分的近似值。
近似随机变量的期望
期望就是随机变量的 "平均取值"，蒙特卡洛方法直接通过抽样求平均，就能近似期望。
比如想知道正态分布随机变量 X 的 X² 的期望：
- 从这个正态分布里随机抽大量样本。
- 对每个样本计算平方值。
- 所有平方值的平均值，就是
X²期望的近似值。
随机梯度下降（SGD）中的应用
随机梯度下降是机器学习的核心优化算法，它的本质就是蒙特卡洛采样的思想。
训练模型时，损失函数的梯度需要计算所有样本的平均梯度，计算量很大。蒙特卡洛的做法是：每次只随机选一个样本，用这个样本的梯度代替所有样本的平均梯度，大幅减少计算量。
三、马尔可夫决策过程
3.1 马尔可夫决策过程基础知识
强化学习的数学基础是马尔可夫决策过程(MarkovDecisionProcesses, MDPs)。马尔可夫决策过程（MDP）通常由状态空间、动作空间、状态转移矩阵、奖励函数及折扣因子构成。强化学习作为一种序贯决策过程，核心目标是寻找最优策略，以最大化系统的累积奖励，实现价值最优。
| 概念 | 简明定义 |
|---|---|
| 状态（State） | 智能体对环境的即时描述，是决策的依据。例如：下棋时的棋盘布局、机器人的当前位置。 |
| 状态空间（State Space） | 环境所有可能状态的集合，记为 S。例如：棋盘的所有合法布局集合、机器人可到达的所有位置集合。 |
| 动作（Action） | 智能体在当前状态下可以执行的操作。例如：下棋时走某一步棋、机器人向前移动。 |
| 动作空间（Action Space） | 智能体在所有状态下可执行动作的集合，记为 A。例如：棋子的所有合法走法、机器人的 "前进 / 后退 / 左转 / 右转" 集合。 |
| 智能体（Agent） | 执行决策、与环境交互的主体，目标是最大化累积奖励。例如：下棋的 AI、自主导航的机器人。 |
| 策略函数（Policy） | 智能体的决策规则 ，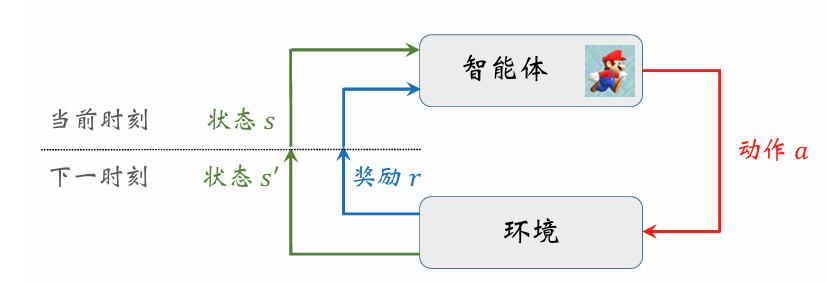
3.2 强化学习的随机性
1. 环境的随机性：状态转移的不确定性
这是强化学习最核心的随机性来源，由环境的动态特性决定，智能体无法直接控制。
- 本质 ：环境遵循随机状态转移函数 P(s′∣s,a)，而非确定性函数 T(s,a)=s′。即智能体在状态 s 执行动作 a 后，不会唯一确定下一个状态，而是以不同概率转移到多个可能的状态。
- 示例
- 机器人走迷宫时，地面湿滑导致执行 "向右" 动作后，有 90% 概率到目标位置，10% 概率滑倒原地。
- 游戏 AI 操控角色攻击时，攻击是否命中、造成多少伤害由概率决定（如暴击率 20%）。
- 自动驾驶中，行人、车辆的行为具有不确定性，即使智能体保持匀速直行，周围环境的状态转移也是随机的。
2. 智能体的随机性：策略的不确定性
智能体的决策规则（策略）本身可以引入随机性，目的是平衡探索与利用。
- 本质 ：智能体采用随机策略 π(a∣s)，而非确定性策略 π(s)=a。即在同一个状态 s 下，智能体不会每次都选择相同的动作，而是按概率分布从动作空间中采样动作。
- 作用：如果策略完全确定，智能体可能会一直选择当前认为最优的动作（利用），而错过更优的动作（探索）；随机策略则能让智能体尝试不同动作，发现潜在的高奖励路径。
- 示例
- 用 ϵ- 贪婪策略训练迷宫机器人：90% 概率选择当前价值最高的动作（如向右），10% 概率随机选择动作（如向上 / 向下），保证对未知路径的探索。
- 强化学习中的策略梯度算法，通常直接优化随机策略的参数（如高斯分布的均值和方差），让智能体在探索中逐步收敛到最优策略。
3. 奖励的随机性：反馈信号的不确定性
部分场景中，环境给予的奖励不是固定值，而是随机变量，进一步增加了强化学习的随机性。
- 本质：奖励函数 r(s,a,s′) 不是确定的数值，而是服从某种概率分布，即相同的 (s,a,s′) 三元组可能对应不同的奖励值。
- 示例
- 机器人完成搬运任务时，奖励可能与物品的完好程度挂钩：成功搬运有 80% 概率获得 + 10 奖励，20% 概率因物品轻微损坏获得 + 5 奖励。
- 金融交易的强化学习模型中，相同的交易动作（如买入某股票）在相同的市场状态下，因市场波动的随机性，获得的收益（奖励）是不确定的。
3.3 回报与折扣回报
回报(Return)是从当前时刻开始到一回合结束的所有奖励的总和。
把 t 时刻的回报记作随机变量 Ut=Rt+Rt+1+Rt+2+Rt+3+···
回报是未来获得的奖励总和，所以智能体的目标就是让回报尽量大，越 大越好。强化学习的目标就是寻找一个策略，使得回报的期望最大化。 注强化学习的目标是最大化回报，而不是最大化当前的奖励。
折扣回报（Discounted Return）
折扣回报是强化学习中衡量智能体长期累积奖励 的核心指标，它给远期奖励赋予一个折扣系数，让近期奖励的权重高于远期奖励。
假设智能体在交互过程中，从时刻 t 开始获得的奖励序列为 rt,rt+1,rt+2,...，折扣回报 Gt 的定义为：
核心意义：
- 符合现实决策逻辑：现实中，当下的收益比未来不确定的收益更有价值（比如今天拿到 100 元，比明年拿到 100 元更有用）。
- 保证数学收敛性：当奖励序列无限长时，折扣机制能让累积奖励的总和成为一个有限值，避免计算发散。
折扣率（Discount Rate）
折扣率 γ 是控制远期奖励折扣程度的超参数，取值范围为 0≤γ≤1。
- γ=0 ：智能体只关注即时奖励 ，
- 0<γ<1：智能体兼顾即时奖励和远期奖励，γ 越接近 1，远期奖励的权重越高。比如 γ=0.9 时，下一个时刻的奖励权重是 0.9，再下一个时刻是 0.81，以此类推。
- γ=1 ：退化为无折扣累积奖励 ，
3.4 价值函数
动作价值函数Qπ(s,a)
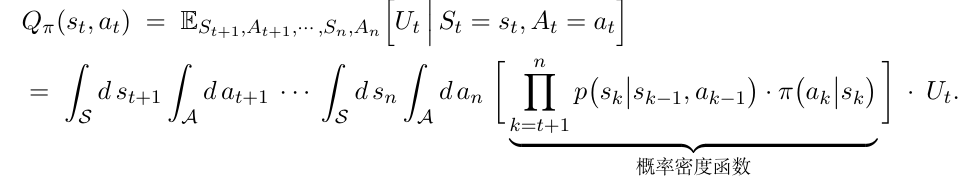
最优动作价值函数Q⋆(s,a)
状态价值函数Vπ(s)
三者的关系：
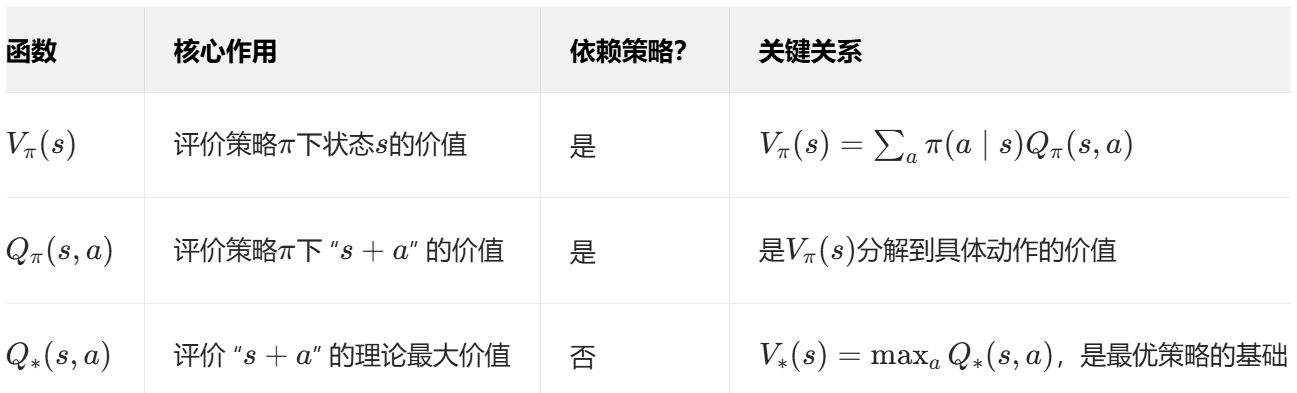
3.5 策略学习和价值学习
强化学习方法通常分为两类：基于模型的方法(Model-Based)和无模 型方法(Model-Free)，无模型方法又可以分为价值学习和策略学习。
基于模型的强化学习（Model-Based RL）
基于模型的强化学习方法的核心是显式构建环境模型 ，即学习状态转移函数 P(s′∣s,a) 和奖励函数 r(s,a,s′)，用这个模型来模拟环境的动态变化。智能体可以利用构建好的模型进行虚拟规划 ：在不与真实环境交互的情况下，通过模型推演不同动作序列的长期回报，从而选择最优策略。这种方法的优势在于样本效率高 ------ 只需少量真实交互数据就能训练出环境模型，再通过模型内的大量虚拟试错优化策略；但缺点也很明显，模型的准确性直接决定策略性能，如果模型与真实环境存在偏差（即 "模型误差"），会导致规划出的策略在真实环境中失效。典型应用场景包括机器人路径规划、棋类 AI 等可建模的领域。
无模型的强化学习（Model-Free RL）
无模型的强化学习方法不依赖环境模型 ，也不试图显式学习状态转移和奖励的规律，而是让智能体直接与真实环境交互，从交互产生的经验数据（状态、动作、奖励、下一个状态） 中学习价值函数或策略。这类方法的核心是 "试错学习"，智能体通过不断探索环境、积累经验，逐步优化决策规则，无需对环境动态进行建模。其最大优势是适用性广 ，能处理复杂、高维、难以建模的真实场景（如自动驾驶、游戏 AI）；但缺点是样本效率低------ 需要大量的真实环境交互数据才能收敛到较好的策略，训练过程往往耗时较长。典型算法包括 Q-learning、SARSA、策略梯度算法等，是当前强化学习在实际场景中应用的主流方法。
价值学习： 通常是指学习最优价值函数 Q⋆(s,a)（或者动作价 值函数、状态价值函数）。
**策略学习：**指的是学习策略函数π(a|s)。假如我们有了策略函 数，我们就可以直接用它计算所有动作的概率值，然后随机抽样选出一个动作并执行。
参考书籍《深度强化学习》