一. 牛客 【模板】01背包
1. 题目解析
背包问题我们可以理解为游戏里拾取装备, 比如三角洲这种, 一个背包有固定空间, 地图上散落一堆道具, 道具有体积, 重量, 价值等等属性, 而我们要做的就是用有限的背包空间来达到拾取道具价值的最大化, 因为道具和背包可以被划分的属性很多, 所以背包问题有很多变种类型, 其中01背包🎒则是最基础最重要的一个模版
这道题是ACM模式, 需要自己处理输入输出和导包
2. 算法原理
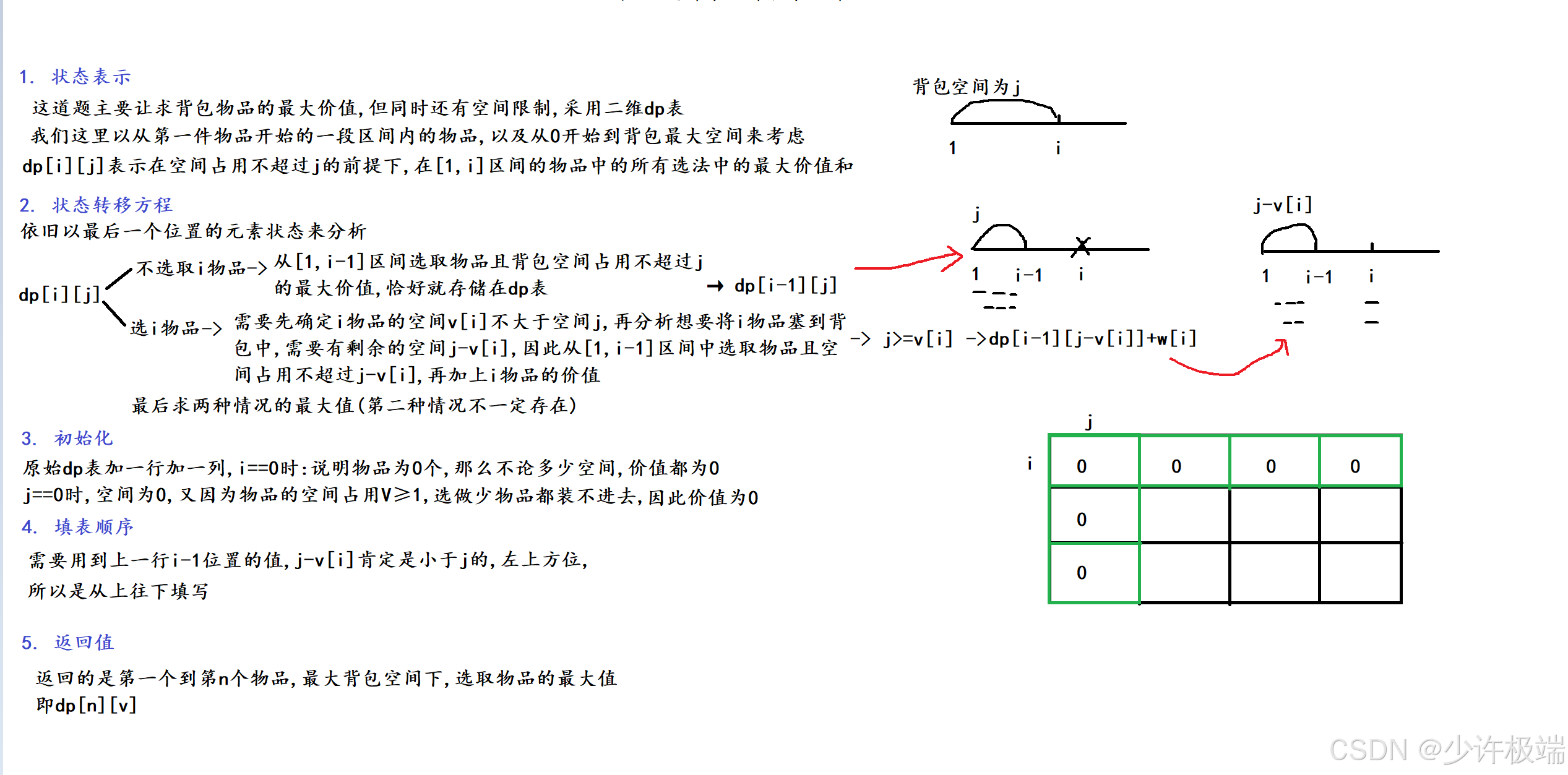
本道题有两问,所以我们分为两次算法原理的图解
第一问图解
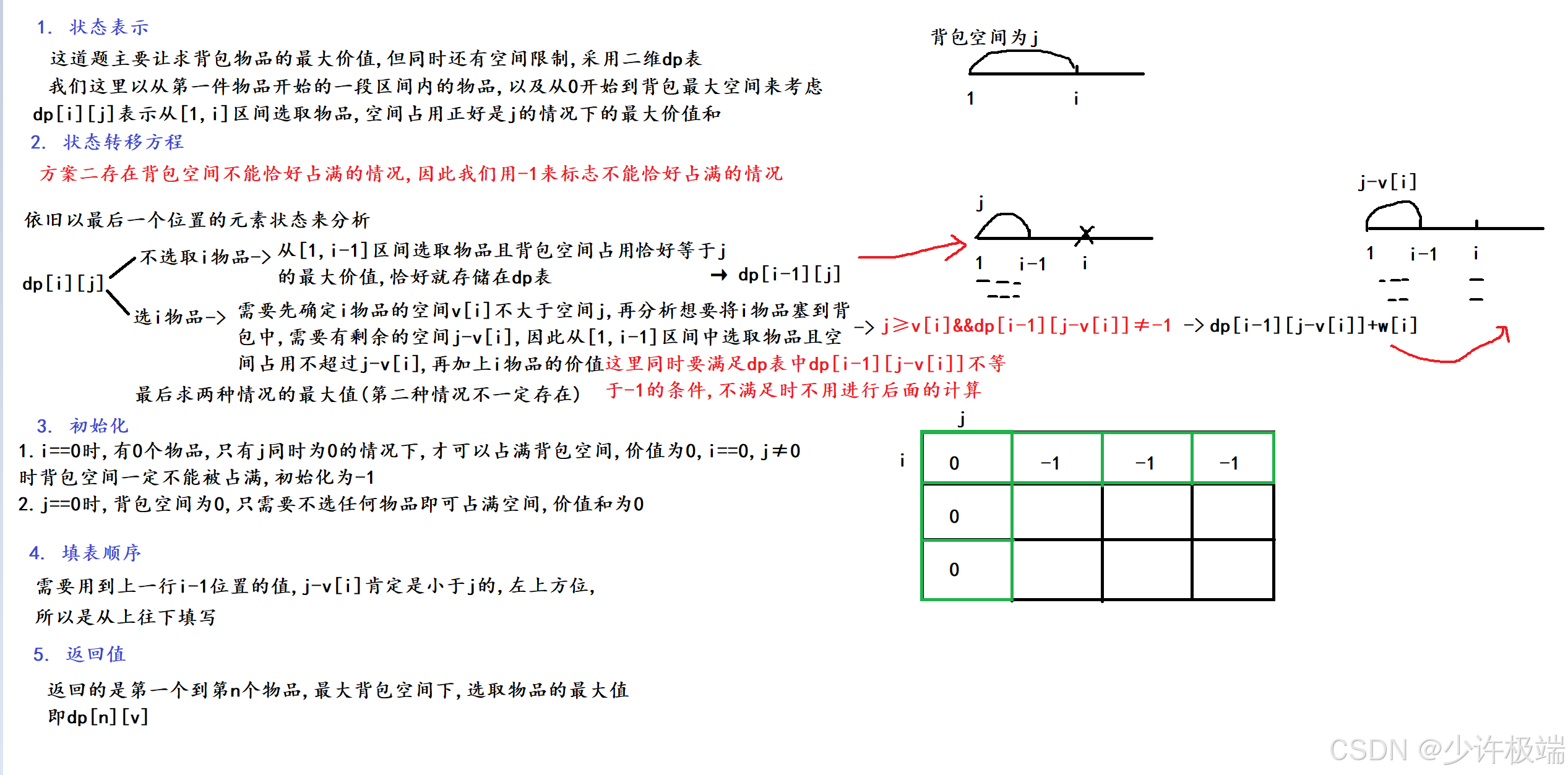
第二问图解
3. 代码
java
import java.util.*;
public class Main {
public static Scanner in = new Scanner(System.in);
public static void main(String[] args) {
// 获取物品个数和体积
int n = in.nextInt();
int V = in.nextInt();
// 建表
int[] v = new int[n + 1];
int[] w = new int[n + 1];
int[][] dp = new int[n + 1][V + 1];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
func1(n, V, v, w, dp);
func2(n, V, v, w, dp);
}
static void func1(int n, int V, int[] v, int[] w, int[][] dp) {
// 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= v[i]) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
// 打印结果
System.out.println(dp[n][V]);
}
static void func2(int n, int V, int[] v, int[] w, int[][] dp) {
// 初始化dp表
for (int j = 1; j <= V; j++) {
dp[0][j] = -1;
}
// 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= v[i] && dp[i - 1][j - v[i]] != -1) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
// 打印结果
System.out.println(dp[n][V] == -1 ? 0 : dp[n][V]);
}
}4. 优化
使用滚动数组来进行空间和时间上的优化
5. 优化后的代码
java
import java.util.*;
public class Main {
public static Scanner in = new Scanner(System.in);
public static void main(String[] args) {
// 获取物品个数和体积
int n = in.nextInt();
int V = in.nextInt();
// 建表
int[] v = new int[n + 1];
int[] w = new int[n + 1];
int[] dp = new int[V + 1];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
func1(n, V, v, w, dp);
func2(n, V, v, w, dp);
}
static void func1(int n, int V, int[] v, int[] w, int[] dp) {
// 填表
for (int i = 1; i <= n; i++) {
for (int j = V; j >= v[i]; j--) { // 这里改成 j >= v[i] 可以减少时间复杂度
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
// 打印结果
System.out.println(dp[V]);
}
static void func2(int n, int V, int[] v, int[] w, int[] dp) {
// 初始化dp表
for (int j = 1; j <= V; j++) {
dp[j] = -1;
}
// 填表
for (int i = 1; i <= n; i++) {
for (int j = V; j >= v[i]; j--) {
if (dp[j - v[i]] != -1) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
}
// 打印结果
System.out.println(dp[V] == -1 ? 0 : dp[V]);
}
}二. 力扣 416. 分割等和子集
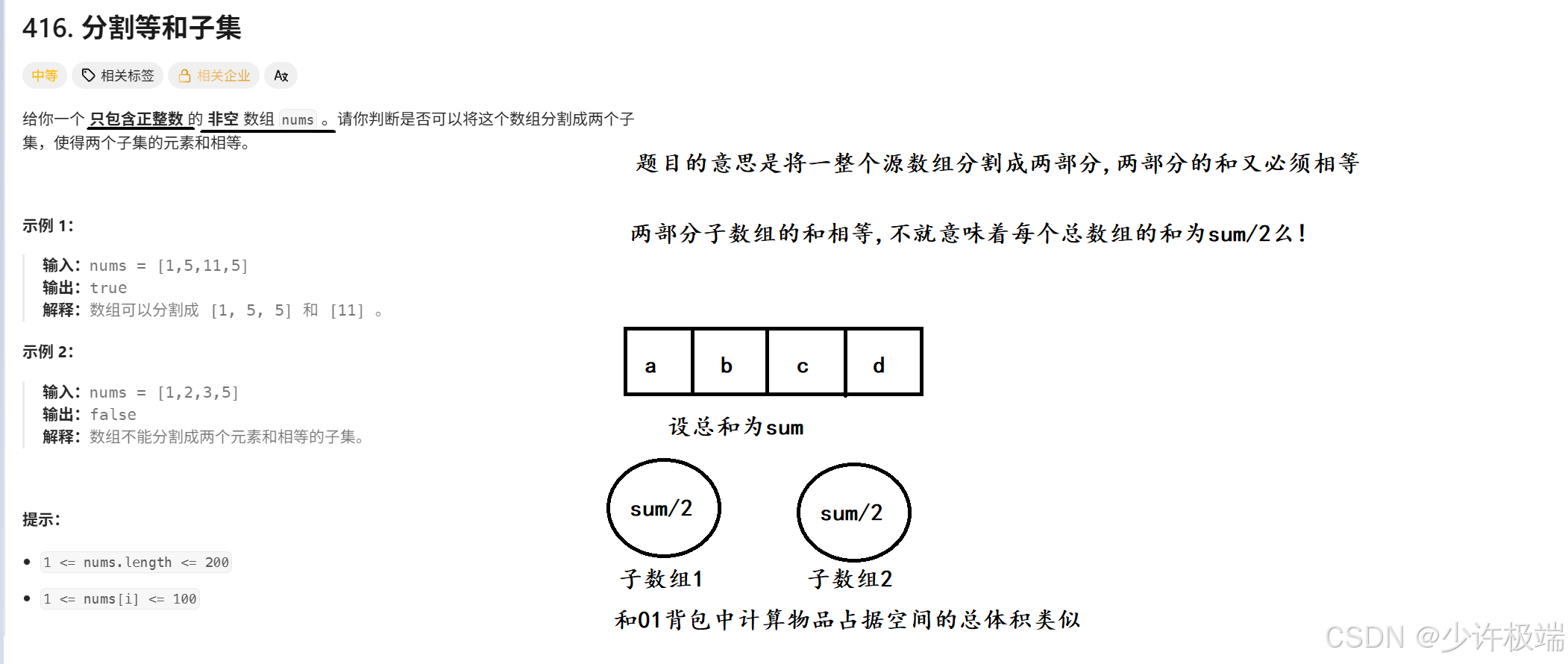
1. 题目解析
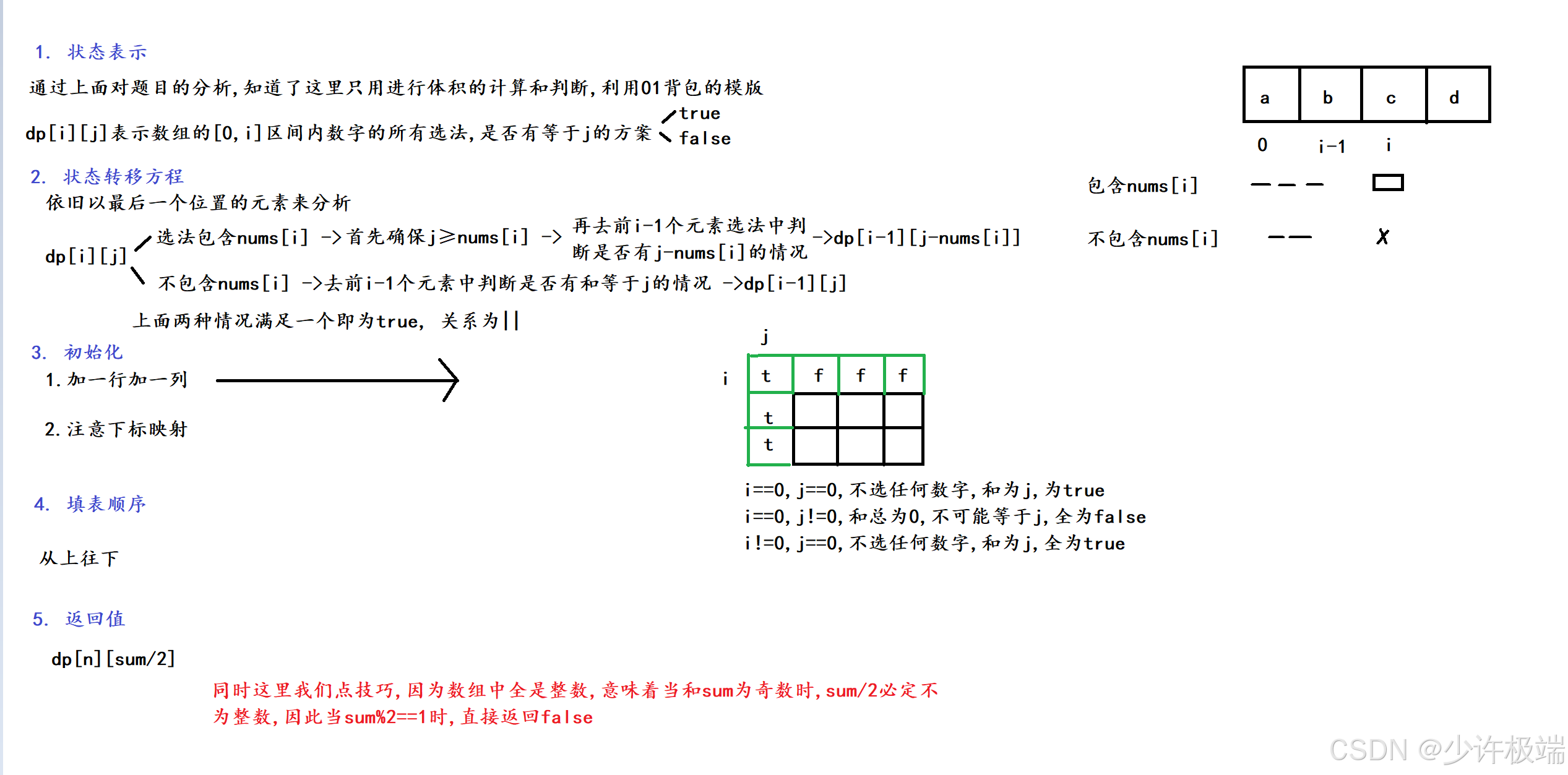
2. 算法原理
刚开始我在想, 为什么不用计算总和, 只用true和false就能表示总和, 后来当我想到是空间1遍历到j的, 意味着[0,i]区间选法的总和是以布尔形式表示了, 自此又进一步懂了一些
3. 代码
java
class Solution {
public boolean canPartition(int[] nums) {
// 建表 求和
int n = nums.length;
int sum = 0;
for (int x : nums) {
sum += x;
}
if (sum % 2 == 1) {
return false;
}
int k = sum / 2;
boolean[][] dp = new boolean[n + 1][k + 1];
// 初始化
for (int i = 0; i <= n; i++) {
dp[i][0] = true;
}
// 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= k; j++) {
if (dp[i - 1][j] || j >= nums[i - 1] && dp[i - 1][j - nums[i - 1]]) {
dp[i][j] = true;
}
}
}
return dp[n][k];
}
}4. 优化
因为这里和01背包的优化方式一样, 这里我们不过多赘述, 直接copy上面图片: ①删除行保留列 ②修改 j 的遍历顺序
5. 优化后的代码
java
class Solution {
public boolean canPartition(int[] nums) {
// 建表 求和
int n = nums.length;
int sum = 0;
for (int x : nums) {
sum += x;
}
if (sum % 2 == 1) {
return false;
}
int k = sum / 2;
boolean[] dp = new boolean[k + 1];
// 初始化
dp[0] = true;
// 填表
for (int i = 1; i <= n; i++) {
for (int j = k; j >= nums[i - 1]; j--) {
if (dp[j - nums[i - 1]]) {
dp[j] = true;
}
}
}
return dp[k];
}
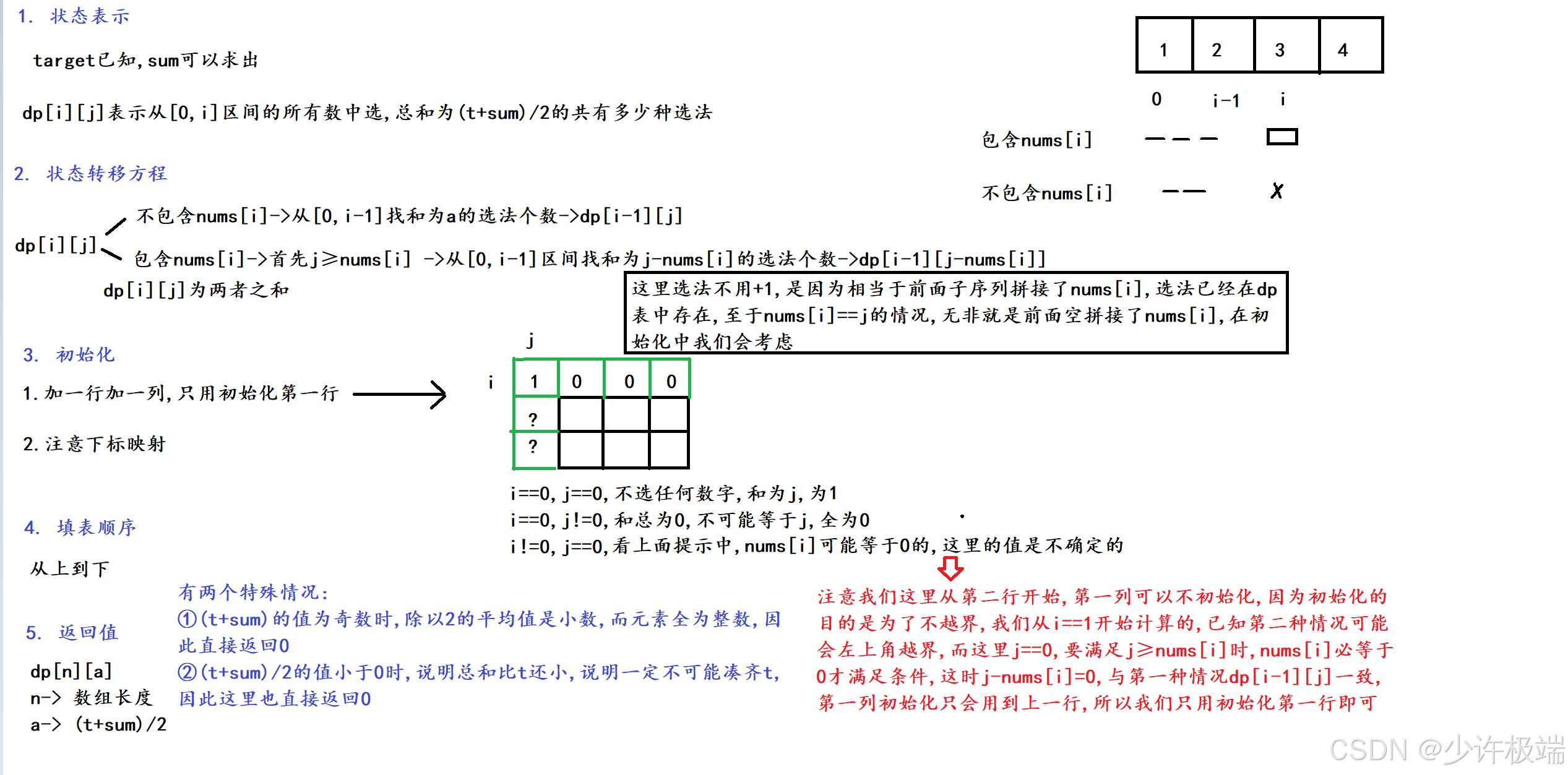
}三. 力扣 494. 目标和
1. 题目解析
2. 算法原理
与01背包原理相似
3. 代码
java
class Solution {
public int findTargetSumWays(int[] nums, int target) {
// 建表
int n = nums.length;
int sum = 0;
for (int x : nums) {
sum += x;
}
int a = (target + sum) / 2;
if ((target + sum) % 2 == 1 || a < 0) {
return 0;
}
int[][] dp = new int[n + 1][a + 1];
// 初始化
dp[0][0] = 1;
// 填表
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= a; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= nums[i - 1]) {
dp[i][j] += dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][a];
}
}4. 优化代码
优化原理仍是滚动数组, 将行删除, j 的遍历顺序改变, 这里就直接上代码
java
class Solution {
public int findTargetSumWays(int[] nums, int target) {
// 建表
int n = nums.length;
int sum = 0;
for (int x : nums) {
sum += x;
}
int a = (target + sum) / 2;
if ((target + sum) % 2 == 1 || a < 0) {
return 0;
}
int[] dp = new int[a + 1];
// 初始化
dp[0] = 1;
// 填表
for (int i = 1; i <= n; i++) {
for (int j = a; j >= nums[i - 1]; j--) {
dp[j] += dp[j - nums[i - 1]];
}
}
return dp[a];
}
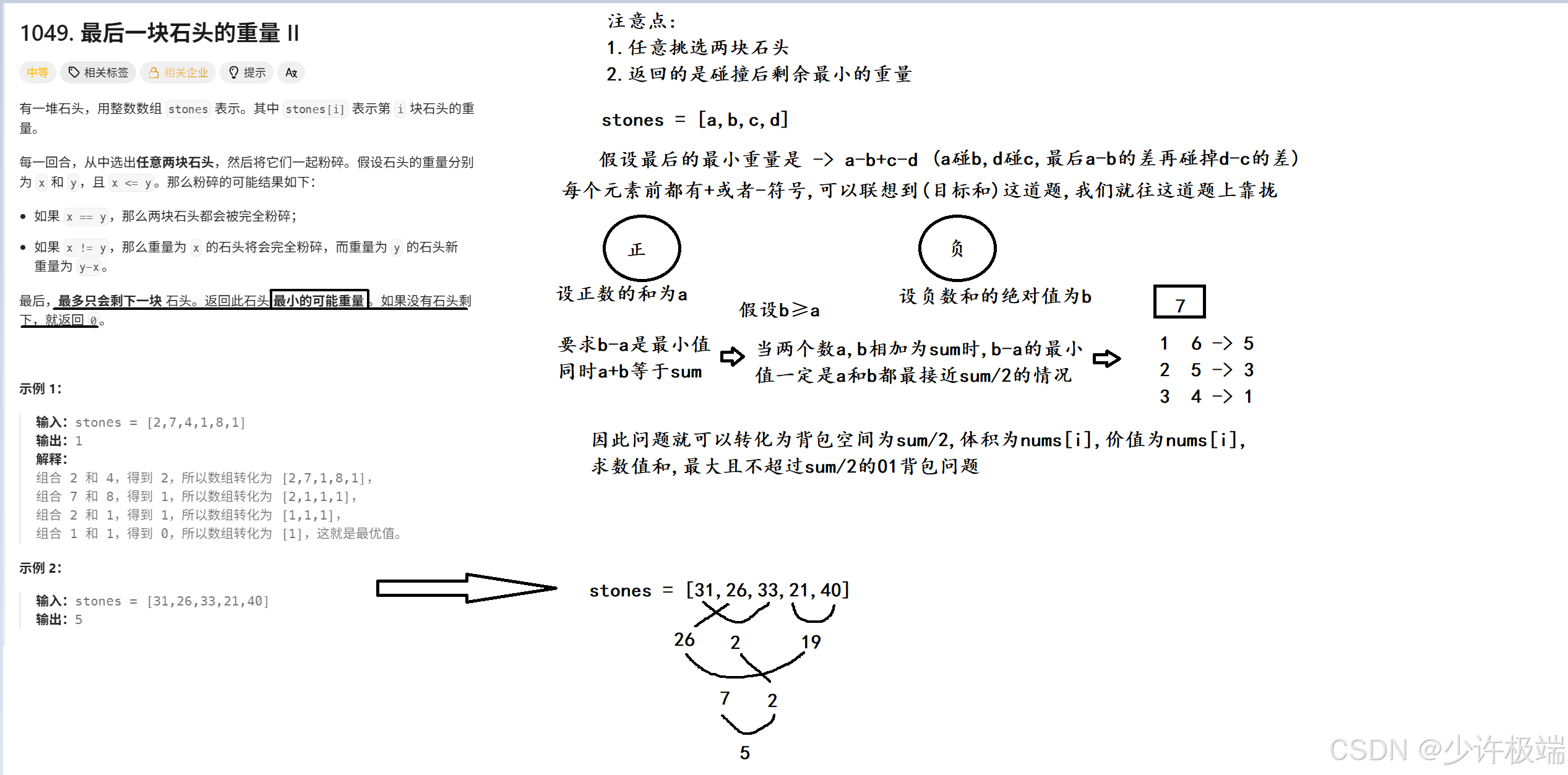
}四. 力扣 1049. 最后一块石头的重量 II
1. 题目解析
这道题最难的就是向01背包问题转化的过程
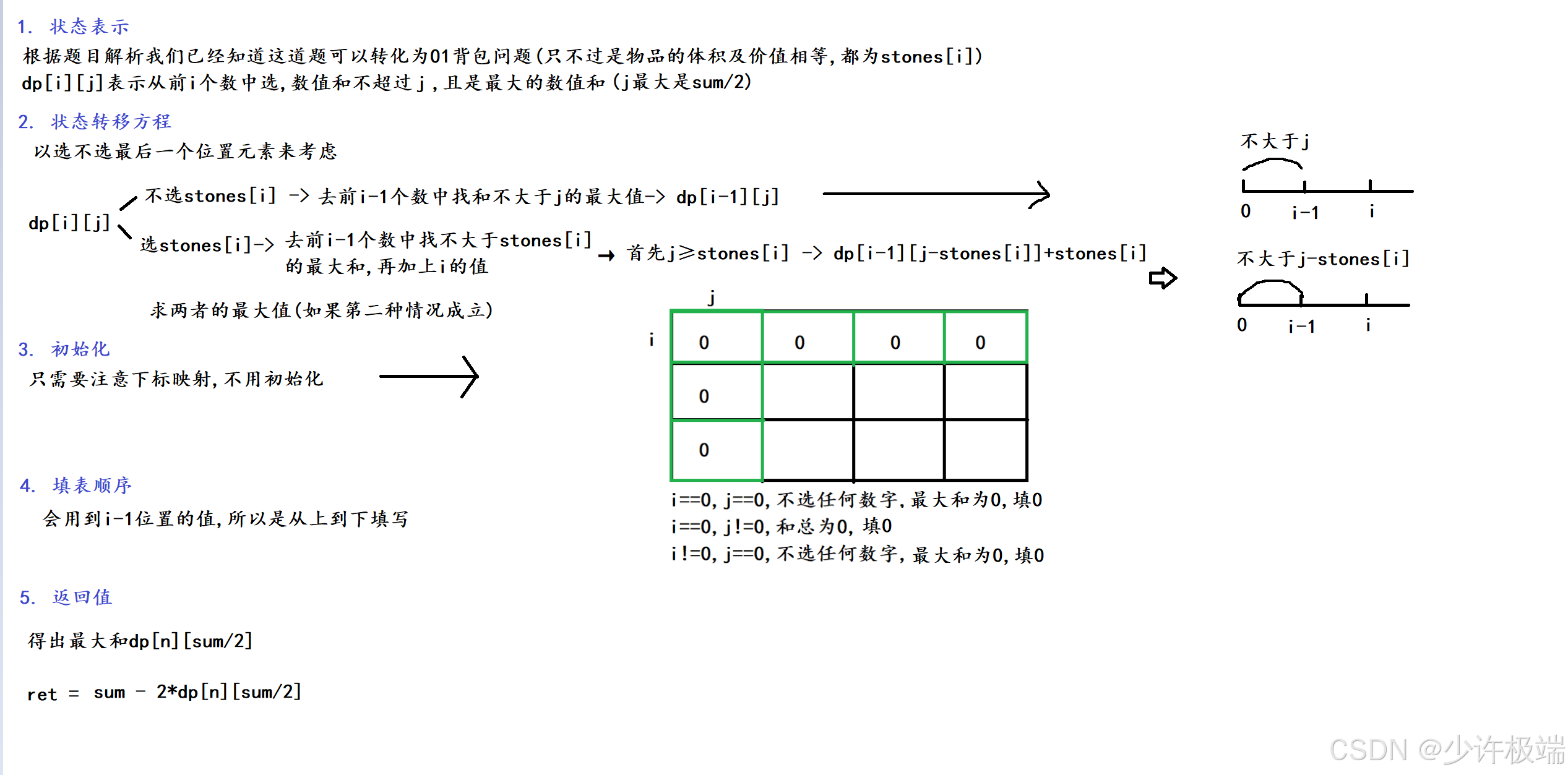
2. 算法原理
算法原理和01背包模版基本上一模一样, 这里简单回顾下
3. 代码
java
class Solution {
public int lastStoneWeightII(int[] stones) {
// 建表,初始化,求和
int n = stones.length;
int sum = 0;
for (int x : stones) {
sum += x;
}
int aim = sum / 2;
int[][] dp = new int[n + 1][aim + 1];
// 填表
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= aim; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= stones[i - 1]) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1]);
}
}
}
// 返回结果
return sum - dp[n][aim] * 2;
}
}4. 优化后的代码
依旧是删除行, j的遍历顺序颠倒过来
java
class Solution {
public int lastStoneWeightII(int[] stones) {
// 建表,初始化,求和
int n = stones.length;
int sum = 0;
for (int x : stones) {
sum += x;
}
int aim = sum / 2;
int[] dp = new int[aim + 1];
// 填表
for (int i = 1; i <= n; i++) {
for (int j = aim; j >= stones[i - 1]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);
}
}
// 返回结果
return sum - dp[aim] * 2;
}
}