【算法竞赛】顺序表和vector

散峰而望2026-01-09 9:01
🔭 个人主页： 散峰而望

《C语言：从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能AI学习》《AI Agent》
愿为出海月，不做归山云

🎬博主简介

【算法竞赛】顺序表和vector

  • 前言
  • [1. 顺序表的概念](#1. 顺序表的概念)
    • [1.1 线性表的定义](#1.1 线性表的定义)
    • [1.2 线性表的顺序存储 --- 顺序表](#1.2 线性表的顺序存储 --- 顺序表)
  • [2. 顺序表的模拟实现](#2. 顺序表的模拟实现)
    • [2.1 顺序表的实现方式](#2.1 顺序表的实现方式)
    • [2.2 创建](#2.2 创建)
    • [2.3 添加元素](#2.3 添加元素)
      • [2.3.1 尾插](#2.3.1 尾插)
      • [2.3.2 头插](#2.3.2 头插)
      • [2.3.3 任意位置插入](#2.3.3 任意位置插入)
    • [2.4 删除一个元素](#2.4 删除一个元素)
      • [2.4.1 尾删](#2.4.1 尾删)
      • [2.4.2 头删](#2.4.2 头删)
      • [2.4.3 任意位置删除](#2.4.3 任意位置删除)
    • [2.5 查找元素](#2.5 查找元素)
      • [2.5.1 按值查找](#2.5.1 按值查找)
      • [2.5.2 按位查找](#2.5.2 按位查找)
    • [2.6 修改元素](#2.6 修改元素)
    • [2.7 清空顺序表](#2.7 清空顺序表)
    • [2.8 所有测试代码](#2.8 所有测试代码)
  • [3. 封装静态顺序表](#3. 封装静态顺序表)
  • [4. 动态顺序表 --- vector](#4. 动态顺序表 --- vector)
    • [4.1 创建 vector](#4.1 创建 vector)
    • [4.2 size / empty](#4.2 size / empty)
    • [4.3 begin / end](#4.3 begin / end)
    • [4.4 push_back / pop_back](#4.4 push_back / pop_back)
    • [4.5 front / back](#4.5 front / back)
    • [4.6 resize](#4.6 resize)
    • [4.6 clear](#4.6 clear)
  • [5. 练题](#5. 练题)
  • 结语

前言

顺序表和 vector 是算法竞赛中最基础且高效的数据结构之一。顺序表通过连续内存存储元素，支持随机访问，而动态扩容的特性使其在不确定数据规模的场景中表现优异。vector 作为 C++ STL 对顺序表的实现，封装了动态数组的核心操作，如尾部插入、中间删除和快速索引，同时通过倍增扩容策略平衡了时间与空间效率。

1. 顺序表的概念

1.1 线性表的定义

线性表是 n 个具有相同特性的数据元素的有序序列。

线性表在逻辑上可以想象成是连续的一条线段，线段上有很多个点，比如下图

cpp 复制代码 
n 个具有相同特性的数据元素的有序序列
          |                  |
  每一个元素的类型一致     有先后顺序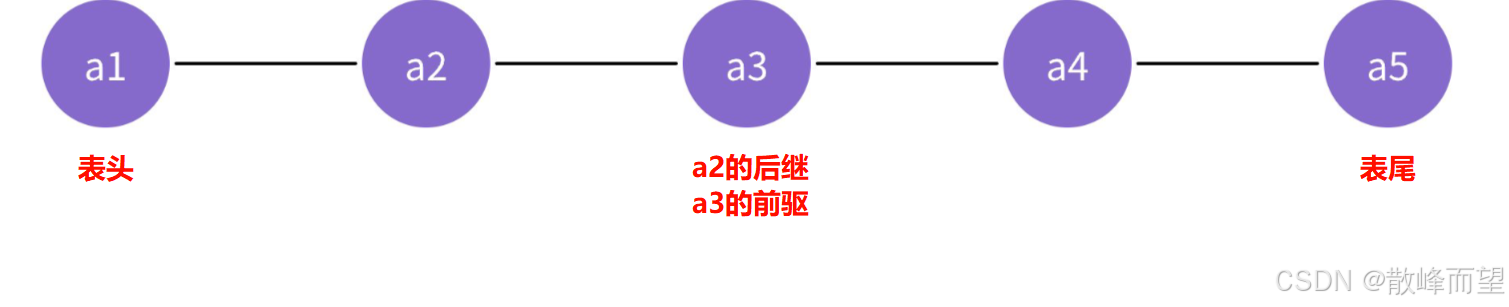

如果一个元素都没有则为 --- 空表。

1.2 线性表的顺序存储 --- 顺序表

线性表的顺序存储就是顺序表。

如果下图中的方格代表内存中的存储单元，那么存储顺序表中 a1 ~ a5 这 5 个元素就是放在连续的位置上：

大家会发现，这不就是用一个数组把这些元素存储起来了嘛？是的，顺序表就是通过数组来实现的。

2. 顺序表的模拟实现

约定：往后实现各种数据结构的时候，如果不做特殊说明，默认里面存储的就是 int 类型的数据

2.1 顺序表的实现方式

按照数组的申请方式，有以下两种实现方式：

  • 数组采用静态分配，此时的顺序表称为静态顺序表 --- int a [N]
  • 数组采用动态分配，此时的顺序表称为动态顺序表 --- new 和 delete

静态分配就是直接向内存申请一大块连续的区域，然后将需要存放的数组放在这一大块连续的区域上。

动态分配就是按需所取。按照需要存放的数据的数量，合理的申请大小合适的空间来存放数据。

实现方式 优点 缺点
静态分配 1. 不需要动态管理内存，代码书写上会比较方便。2. 没有动态管理内存中申请以及释放空间的时间开销。 1. 一旦空间占满，新来的数据就会溢出。2. 如果为了保险而申请很大的空间，数据量小的情况下，会浪费很多空间。
动态分配 1. 自由的分配空间。数据量小，就用申请小内存；数据量大，就在原有的基础上扩容。 1. 由于需要动态管理内存，代码书写上会比较麻烦。2. 动态内存的过程中会经常涉及扩容，而扩容需要申请空间，转移数据，释放空间。这些操作会有大量的时间消耗。

这里简单介绍一下动态分配

例：往顺序表插入 [1, 2, 3, 4...10]
int * a;//接收 new 出来的数组的地址
int capacity;//标记当前数组的实际大小
int n;//标记有效元素的个数

  1. 第一次空间不够，扩容：
cpp 复制代码 
a = new int[4];
capacity = 4;
  1. 第二次空间不够，扩容：
cpp 复制代码 
int * t = new int[capacity * 2];
memcpy(t, a, sizeof(int) * capacity);
delete[] a;
a = t;
capacity *= 2;
  1. 第三次空间不够，扩容：
cpp 复制代码 
int * t = new int[capacity * 2];
memcpy(t, a, sizeof(int) * capacity);
delete[] a;
a = t;
capacity *= 2;

通过两者对比会发现，并没有一种实现方式就是绝对完美的。想要书写方便以及运行更快，就要承担空间不够或者空间浪费的情况；想要空间上合理分配，就要承担时间以及代码书写上的消耗。

在后续的学习中，会经常看到各种情况的对比。这就要求我们掌握各种数据结构的特点，从而在解决实际问题的时候，选择一个合适的数据结构。

在算法竞赛中，我们主要关心的其实是时间开销，空间上是基本够用的。因此，定义一个超大的静态数组来解决问题是完全可以接受的。因此，关于顺序表，采用的就是静态实现的方式。

2.2 创建

cpp 复制代码 
const int N = 1e6 + 10; // 定义静态数组的最大⻓度 
int a[N], n; // 直接创建一个大数组来实现顺序表， n 表示当前有多少个元素

约定：下标为 0 的位置，不存储有效数据，也就是说我们从 a[1]开始存储 --- 把下标为 0 空出来，方便处理一些边界情况

2.3 添加元素

2.3.1 尾插

cpp 复制代码 
//尾插 
void push_back(int x)
{
    a[++n] = x; // 下标为 0 的位置空出来 
    
    // 这样操作一般根据个人习惯，也可以从 0 开始计数，也可以从其他位置开始计数 
    // 不过有些问题从 1 计数，处理起来可以不用考虑边界情况  
}

思考，这个函数有 bug 么？

  1. 数组存满了，就不能再存了！

我们一般不去管这个判断怎么写，因为我们在调用的时候，自己会判断合不合法，如果不合法，我们是不会调用的。

时间复杂度：

直接放在后面即可，时间复杂度为 O(1)

2.3.2 头插

有三个策略可以让实现头插：

  • 策略一： 直接放在表头 --- a[1] = 10;
  • 策略二： 放在之前空出来的位置上 --- a[0] = 10;
  • 策略三： 将顺序表所有元素统一右移一位，然后再放到表头

可以看到最好的实现方法是策略三。

同时策略三 又有两种移动方式：

  • 移动方式一：从前往后一个一个移动 --- 不行，会覆盖后面的元素
  • 移动方式二：从后往前 一个一个移动
    1.将[1, n]内所有元素右移一位
    2.新的元素放在表头
    3.修改元素的个数
cpp 复制代码 
//头插
void push_front(int x)
{
	//要把所有的元素全部右移一位，然后放到头部位置 
	for(int i = n; i >= 1; i--)
	{
		a[i + 1] = a[i];
	}
	a[1] = x;//把x放在首位 
	n++;//不要忘记总个数 +1 
 }

思考，这个函数有 bug 么？

判断数组是否存满，不过都是自己判断

时间复杂度：

由于需要将所有元素右移一位，时间复杂度 O(N)

2.3.3 任意位置插入

类比头插，相当于把头删的头部位置 移到p位置 插入，故需要传一个 p 表示位置 ，插入一个数 x 。

cpp 复制代码 
//任意位置插
void insert(int p, int x)
{
	for(int i = n; i >= p; i--)
	{
		a[i + 1] = a[i];
	}
	n++;//总个数+1 
 }

思考，这个函数有 bug 么？

p 的位置要是合法的要在 [1, n] 内部，数组是否存满，同样这个由自己判断

2.4 删除一个元素

2.4.1 尾删

有一个方法就是将尾部的元素变为 0 ，然后再让数目减一。但是 我们可以直接减减即可，不管尾部存储的是什么元素，都不会读取那个位置。

cpp 复制代码 
//尾删
void pop_back()
{
	n--;
 }

思考，这个函数有 bug 么？

删除之前，要判断一下顺序表里面是否有元素

时间复杂度：

显然是 O(1)

2.4.2 头删

删除头部的元素，然后让所有的元素向前移动一位。

同样移动方式有两种：

  • 移动方式一：从前往后一个一个移动
  • 移动方式二：从后往前一个一个移动 --- 不行，会覆盖前面的元素
cpp 复制代码 
//头删
void pop_front()
{
	//把所有元素向前移动一位
	for(int i = 2; i <= n; i++)
	{
		a[i - 1] = a[i];
	 } 
	 n--;
 }

思考，这个函数有 bug 么？

删除之前，要判断一下顺序表里面是否有元素

2.4.3 任意位置删除

类比头删，相当于把头删的头部位置 移到p位置 删除，故只需要传一个 p 就行了，然后让 p 位置后的元素前移。

cpp 复制代码 
//任意位置插
void erase(int p)
{
	for(int i = p + 1; i <= n; i++)
	{
		a[i - 1] = a[i];
	 } 
	 n--;//总个数-1 
 }

思考，这个函数有 bug 么？

p 的位置要是合法的要在 [1, n] 内部，判断顺序表里面是否有元素，同样这个由自己判断

时间复杂度：

最坏情况下，所有元素都需要左移，即为 O(N)

2.5 查找元素

2.5.1 按值查找

策略： 从前往后遍历整个顺序表判断遍历的元素是否等于要查找的值

cpp 复制代码 
//按值查找
int find(int x)
{
	for(int i = 1; i <= n; i++)
	{
		if(a[i] == x) return i;
	}
	return 0;
 }

时间复杂度：

最坏的情况下需要遍历所有数组，时间复杂度 O(N)

2.5.2 按位查找

直接找其对应的下标

cpp 复制代码 
//按位查找
int at(int p)
{
	return a[p];
 }

思考，这个函数有 bug 么？

p 的位置要是合法的要在 [1, n] 内部

时间复杂度：

这就是顺序表随机存取 的特性，只要给我一个下标，就能快速访问该元素。时间复杂度 O(1)

2.6 修改元素

指出要修改元素的下标

cpp 复制代码 
//修改元素
//把p位置的数修改成x
void change(int p, int x)
{
	a[p] = x;
 }

思考，这个函数有 bug 么？

p 的位置要是合法的要在 [1, n] 内部

时间复杂度：

这就是顺序表随机存取 的特性，只要给我一个下标，就能快速访问该元素。时间复杂度 O(1)

2.7 清空顺序表

cpp 复制代码 
//清空顺序表
void clear()
{
	n = 0;
 }

有些情况会出现问题，如果存的是 int* 指针，每个指针搞一个 new 数组即申请一块空间。如果这些让 n 直接为 0 的话，new 出来的空间没有释放，造成内存泄漏 。正常的应该是先 delete 掉，再 n-- 遍历释放。

时间复杂度：

要注意，我们自己实现的简单形式是 O(1)

但是，严谨的方式应该是 O(N)

2.8 所有测试代码

cpp 复制代码 
#include <iostream>
using namespace std;

const int N = 1e6 + 10;

int a[N];
int n;

// 打印顺序表 
void print()
{
    for(int i = 1; i <= n; i++)
    {
        cout << a[i] << " ";
    }
    cout << endl << endl;
}    

//尾插
void push_back(int x)
{
	a[++n] = x;
 } 



//头插
void push_front(int x)
{
	//要把所有的元素全部右移一位，然后放到头部位置 
	for(int i = n; i >= 1; i--)
	{
		a[i + 1] = a[i];
	}
	a[1] = x;//把x放在首位 
	n++;//不要忘记总个数 +1 
 } 



//任意位置插
void insert(int p, int x)
{
	for(int i = n; i >= p; i--)
	{
		a[i + 1] = a[i];
	}
	n++;//总个数+1 
 } 




//尾删
void pop_back()
{
	n--;
 } 
 
 
 
//头删
void pop_front()
{
	//把所有元素向前移动一位
	for(int i = 2; i <= n; i++)
	{
		a[i - 1] = a[i];
	 } 
	 n--;
 } 



//任意位置删 
void erase(int p)
{
	for(int i = p + 1; i <= n; i++)
	{
		a[i - 1] = a[i];
	 } 
	 n--;//总个数-1 
 } 
 


//按值查找
int find(int x)
{
	for(int i = 1; i <= n; i++)
	{
		if(a[i] == x) return i;
	}
	return 0;
 } 



//按位查找
int at(int p)
{
	return a[p];
 } 



//修改元素
void change(int p, int x)
{
	a[p] = x;
 } 



//清空顺序表
void clear()
{
	n = 0;
 } 



int main()
{
	// 测试尾插 
    push_back(2);
    print();
    push_back(5);
    print();
    push_back(1);
    print();
    push_back(3);
    print();
    // 测试头插 
    push_front(10);
    print();
    // 测试任意位置插入 
    insert(3, 0);
    print();
    // 测试尾删 
     cout << "尾删：" << endl; 
     pop_back();
     print();
     pop_back();
     print();
     pop_front();
     pop_front();
     print();
    // 测试任意位置删除 
    // cout << "任意位置删除：" << endl; 
    // erase(3);
    // print();
    // erase(2);
    // print();
    // erase(4);
    // print();
    for(int i = 1; i <= 10; i++)
    {
        cout << "查找" << i << ": ";
        cout << find(i) << endl;
    }
    return 0;
}

3. 封装静态顺序表

思考一下，如果实际情况需要特别多的顺序表来解决问题，上述的写法有什么问题么？

如果需要两个及以上的顺序表：

  • 定义数组的时候就需要定义多个 a1, a2....，还需要配套的 n1,n2...，来描述顺序表的大小；
  • 在调用 push_back 等函数的时候，还需要将 a1 和 n1 作为参数传进去，不然不知道修改的是哪一个顺序表；
  • 传参的时候还需要注意传引用，因为顺序表的大小有可能改变，我们要修改 ni 的值

比如：

cpp 复制代码 
#include <iostream>
using namespace std;
const int N = 1e6 + 10; // 根据实际情况而定 
// 创建顺序表 
// int a[N]; // 用足够大的数组来模拟顺序表 
// int n; // 标记顺序表里面有多少个元素 
// 需要多个顺序表，才能解决问题 
int a1[N], n1;
int a2[N], n2;
int a3[N], n3;
// 打印顺序表 
void print()
{
    for(int i = 1; i <= n; i++)
    {
        cout << a[i] << " ";
    }
    cout << endl << endl;
}
// 尾插 
void push_back(int a[], int& n, int x)
{
    a[++n] = x;
}

可以看到不仅要用 int a[] 传入要插入的数组，还要用 int& n 来影响外面的 n 。

可见，如果需要多个顺序表时，上述代码虽然能很大程度上继续复用，但还是比较麻烦。那么应该如何解决这个问题呢？

利用 C++ 中的结构体和类 把我们实现的顺序表封装起来，就能简化操作。

cpp 复制代码 
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
// 将顺序表的创建以及增删查改封装在一个类中 
class SqList
{
    int a[N];
    int n;
public:
    // 构造函数，初始化
    SqList()
    {
        n = 0;
    }
    // 尾插 
    void push_back(int x)
    {
        a[++n] = x;
    }
    // 尾删 
    void pop_back()
    {
        n--;
    }
    // 打印 
    void print()
    {
        for(int i = 1; i <= n; i++)
        {
            cout << a[i] << " ";
        }
        cout << endl;
    }
};
int main()
{
    SqList s1, s2; // 创建了两个顺序表 
    for(int i = 1; i <= 5; i++)
    {
        // 直接调用 s1 和 s2 里面的 push_back 
        s1.push_back(i);
        s2.push_back(i * 2);
    }
    s1.print();
    s2.print();
    for(int i = 1; i <= 2; i++)
    {
        s1.pop_back();
        s2.pop_back();
    }
    
    s1.print();
    s2.print();
    return 0;
}

用类和结构体将代码进行封装，能够很大程度上减少重复的操作，使代码的复用率大大提升。

注意：

  • 为什么这里讲了封装？
    最重要的原因是想让大家知道，接下来我们要学习的 STL 为什么可以通过 "." 调用各种各样的接口。
  • 为什么我们后面不做封装了？
    a. 我们做题如果用到某个数据结构，一般仅需要一个，最多两个，所以没有必要封装。因为封装之后，还要去写 xxx.xxx ，比较麻烦；
    b. 如果要用到多个相同的数据结构，那么推荐使用 STL ，更加方便。

4. 动态顺序表 --- vector

动态顺序表就不带着实现了，因为涉及空间申请和释放的 new 和 delete 效率不高，在算法竞赛中使用会有超时的风险。而且实现一个动态顺序表代码量很大，我们不可能在竞赛中傻乎乎的实现一个动态顺序表来解决问题。

如果需要用动态顺序表，有更好的方式：C++ 的 STL 提供了一个已经封装好的容器 --- vector，有的地方也叫作可变长的数组。vector 的底层就是一个会自动扩容的顺序表，其中创建以及增删查改等等的逻辑已经实现好了，并且也完成了封装。

接下来就重点学习 vector 的使用。

4.1 创建 vector

cpp 复制代码 
#include <vector> // 头文件 
using namespace std;
const int N = 20;
struct node
{
    int a, b, c;
};
// 1. 创建 
void init()
{
    vector<int> a1; // 创建一个空的可变⻓数组 
    vector<int> a2(N); // 指定好了一个空间，大小为 N 
    vector<int> a3(N, 10); // 创建一个大小为 N 的 vector，并且里面的所有元素都是 10 
    vector<int> a4 = {1, 2, 3, 4, 5}; // 使用列表初始化，创建一个 vector 
    // <> 里面可以放任意的类型，这就是模板的作用，也是模板强大的地方 
    // 这样，vector 里面就可以放我们接触过的任意数据类型，甚至是 STL 
    vector<string> a5; // 放字符串 
    vector<node> a6; // 放一个结构体 
    vector<vector<int>> a7; // 甚至可以放一个自己，当成一个二维数组来使用。并且每一维都是可变的 
    
    vector<int> a8[N]; // 创建 N 个 vector 
}

4.2 size / empty

  1. size：返回实际元素的个数；
  2. empty：返回顺序表是否为空，因此是一个 bool 类型的返回值。
    a. 如果为空：返回 true
    b. 否则，返回 false

时间复杂度：

O(1)

cpp 复制代码 
// 2. size
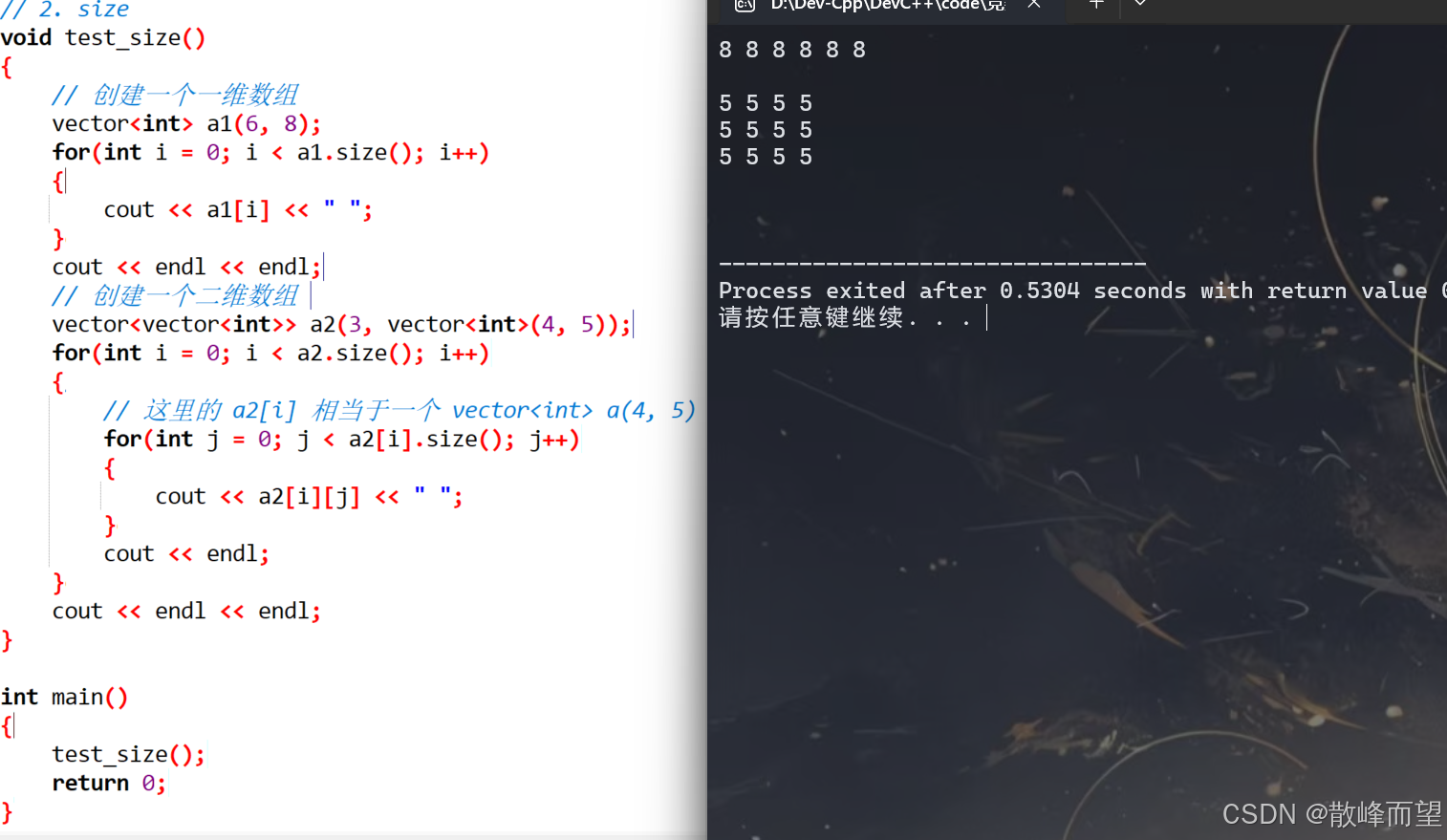
void test_size()
{
    // 创建一个一维数组 
    vector<int> a1(6, 8);
    for(int i = 0; i < a1.size(); i++)
    {
        cout << a1[i] << " ";
    }
    cout << endl << endl;
    // 创建一个二维数组 
    vector<vector<int>> a2(3, vector<int>(4, 5));
    for(int i = 0; i < a2.size(); i++)
    {
        // 这里的 a2[i] 相当于一个 vector<int> a(4, 5) 
        for(int j = 0; j < a2[i].size(); j++)
        {
            cout << a2[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl << endl;
}

演示结果：

4.3 begin / end

  1. begin：返回起始位置的迭代器（左闭）；
  2. end：返回终点位置的下一个位置的迭代器（右开）；
    利用迭代器可以访问整个 vector，存在迭代器的容器就可以使用范围 for 遍历。
cpp 复制代码 
// 3. begin/end
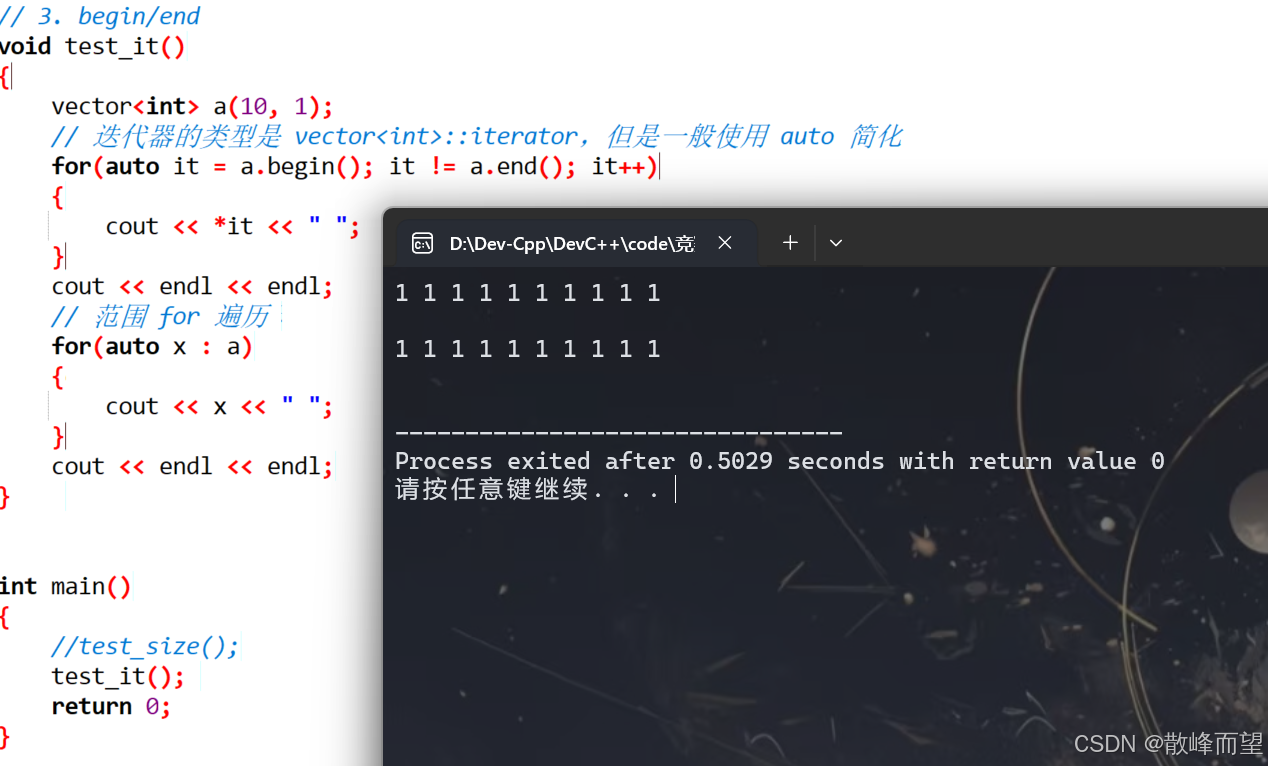
void test_it()
{
    vector<int> a(10, 1);
    // 迭代器的类型是 vector<int>::iterator，但是一般使用 auto 简化 
    for(auto it = a.begin(); it != a.end(); it++)
    {
        cout << *it << " ";
    }
    cout << endl << endl;
    // 范围 for 遍历 
    for(auto x : a)
    {
        cout << x << " ";
    }
    cout << endl << endl;
}

演示结果：

4.4 push_back / pop_back

  1. push_back：尾部添加一个元素
  2. pop_back：尾部删除一个元素

当然还有 insert 与 erase。不过由于时间复杂度过高，尽量不使用。

时间复杂度：

O(1)

cpp 复制代码 
// 如果不加引用，会拷贝一份，时间开销很大 
void print(vector<int>& a)
{
    for(auto x : a)
    {
        cout << x << " ";
    }
    cout << endl;
}
// 4. 添加和删除元素 
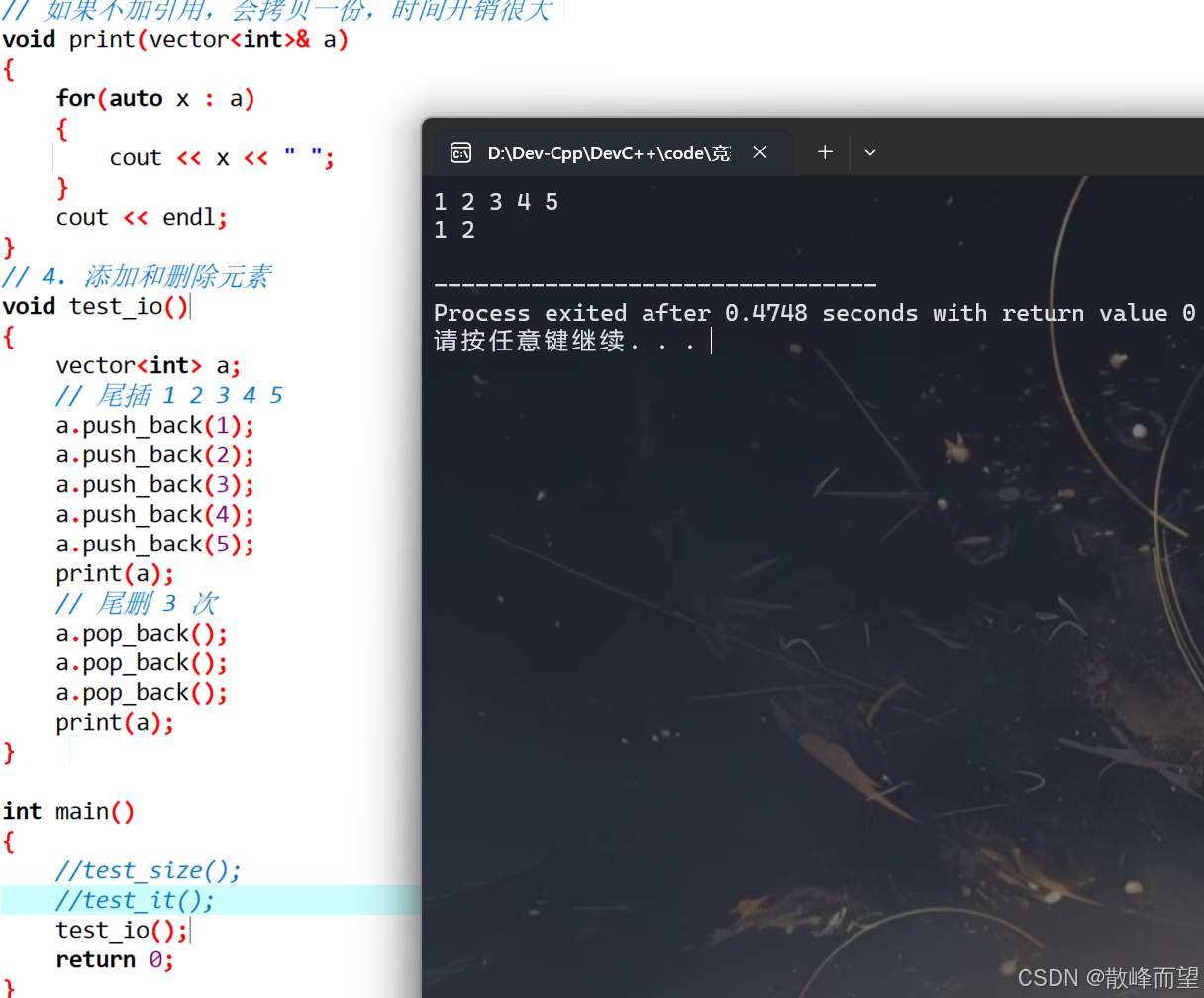
void test_io()
{
    vector<int> a;
    // 尾插 1 2 3 4 5 
    a.push_back(1);
    a.push_back(2);
    a.push_back(3);
    a.push_back(4);
    a.push_back(5); 
    print(a);
    // 尾删 3 次 
    a.pop_back();
    a.pop_back();
    a.pop_back();
    print(a);
}

演示结果：

4.5 front / back

  1. front：返回首元素；
  2. back：返回尾元素；

时间复杂度：

O(1)

cpp 复制代码 
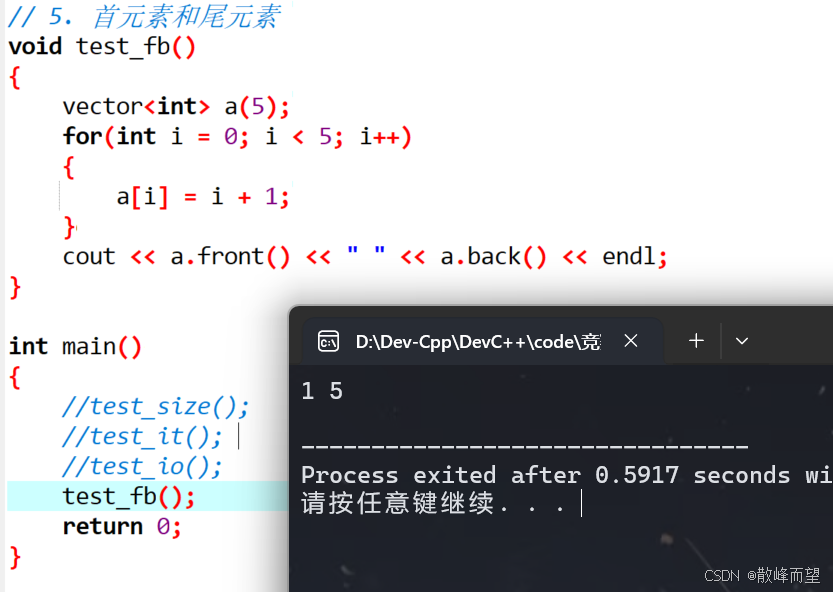
// 5. 首元素和尾元素 
void test_fb()
{
    vector<int> a(5);
    for(int i = 0; i < 5; i++)
    {
        a[i] = i + 1;
    }
    cout << a.front() << " " << a.back() << endl;
}

演示结果：

4.6 resize

  • 修改 vector 的大小。
  • 如果大于原始的大小，多出来的位置会补上默认值，一般是 0 。
  • 如果小于原始的大小，相当于把后面的元素全部删掉。

时间复杂度：

O(1)

cpp 复制代码 
// 如果不加引用，会拷⻉一份，时间开销很大 
void print(vector<int>& a)
{
    for(auto x : a)
    {
        cout << x << " ";
    }
    cout << endl;
}
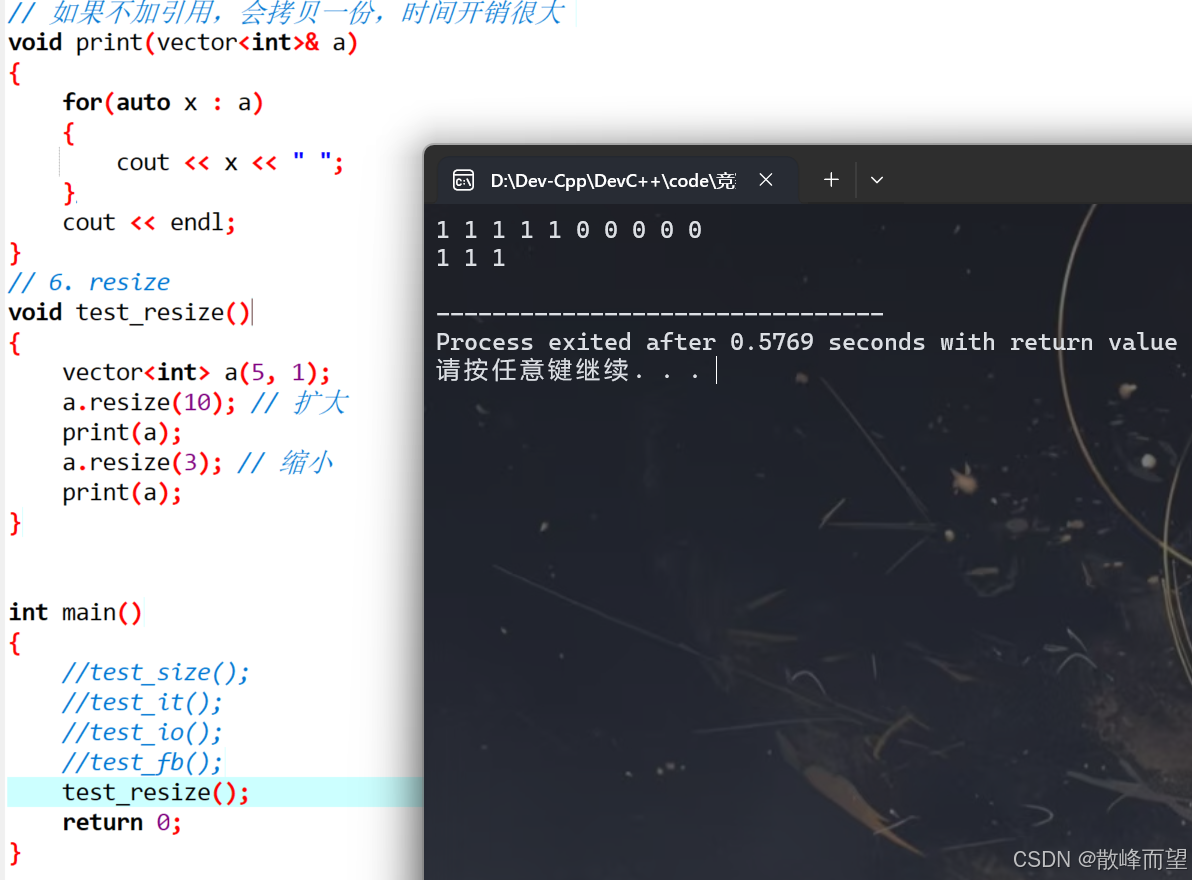
// 6. resize
void test_resize()
{
    vector<int> a(5, 1);
    a.resize(10); // 扩大 
    print(a);
    a.resize(3); // 缩小 
    print(a);
}

演示结果：

4.6 clear

  • 清空 vector

时间复杂度：

底层实现的时候，会遍历整个元素，一个一个删除，因此时间复杂度：O(N)

cpp 复制代码 
// 如果不加引用，会拷贝一份，时间开销很大 
void print(vector<int>& a)
{
    for(auto x : a)
    {
        cout << x << " ";
    }
    cout << endl;
}
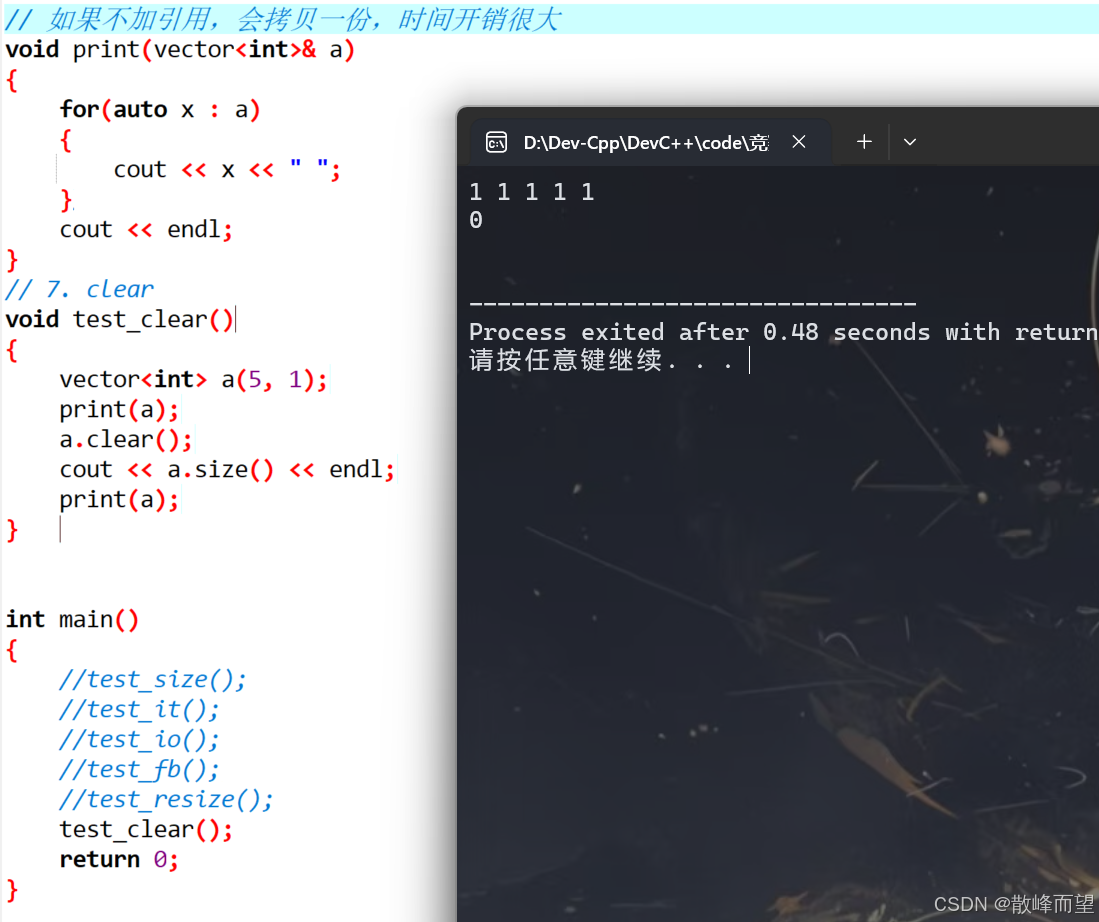
// 7. clear
void test_clear()
{
    vector<int> a(5, 1);
    print(a);
    a.clear();
    cout << a.size() << endl;
    print(a);
}

演示结果：

vector 内封装的接口其实还有很多，比如：

  • insert：在指定位置插入一个元素；
  • erase：删除指定位置的元素；
  • ...

但是，其余的接口要么不常用；要么时间复杂度较高，比如 insert 和 erase，算法竞赛中不能频繁的调用。因此，在这里以及往后，介绍的都是常用以及高效的接口。

另外，在 https://cplusplus.com/ 里，可以查阅各种容器中的接口，以及使用方式。

5. 练题

  1. 询问学号

  2. 寄包柜

  3. 移动零

  4. 合并两个有序数组

  5. The Blocks Problem

结语

顺序表作为线性表最基础的存储结构，其连续存储的特性使得随机访问效率极高，在算法竞赛和实际开发中具有重要地位。通过静态数组模拟实现顺序表，能够深入理解底层内存管理和数据操作逻辑，为后续学习动态顺序表打下基础。

动态顺序表（如 C++ 的 vector）在静态顺序表的基础上引入了自动扩容机制，兼顾了灵活性和效率，成为算法竞赛中最常用的容器之一。掌握 vector 的常用操作（插入、删除、查找、扩容等）以及迭代器的使用，能显著提升代码编写速度和运行性能。

建议通过实际题目练习巩固顺序表和 vector 的应用，例如数组元素操作、滑动窗口、动态规划等场景。理解底层实现原理的同时，也要学会合理调用标准库工具，在性能与开发效率之间找到平衡。

愿诸君能一起共渡重重浪，终见缛彩遥分地，繁光远缀天。

相关推荐
墨染天姬17 小时前
【AI】OCR开源模型排行
人工智能·开源·ocr
幻云201017 小时前
Python机器学习：从入门到资深
人工智能·python
泰迪智能科技17 小时前
分享|企业数据挖掘平台产品功能
人工智能·数据挖掘
黎雁·泠崖17 小时前
二叉树实战进阶全攻略：从层序遍历到OJ题深度解析
c语言·数据结构·leetcode
欧阳天风17 小时前
用setTimeout代替setInterval
开发语言·前端·javascript
千金裘换酒17 小时前
LeetCode 回文链表
算法·leetcode·链表
CSDN_RTKLIB17 小时前
【std::map】与std::unordered_map差异
算法·stl·哈希算法
FL1717131417 小时前
Geometric Control
人工智能·算法
小鸡脚来咯17 小时前
Java字符串详解
java·开发语言
热门推荐
01GitHub 镜像站点02安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）03Linux下V2Ray安装配置指南04Labelme从安装到标注：零基础完整指南05jdk21下载、安装（Windows、Linux、macOS）06【踩坑笔记】50系显卡适配的 PyTorch 安装07手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！08Opencode CLI 安装成功,但是启动失败09GitLab 零基础入门指南：从安装到项目管理全流程10Claude Code Plan 模式完全指南：从入门到精通