
| 🔭 个人主页: 散峰而望 |
|---|
《C语言:从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月,不做归山云
🎬博主简介



【算法竞赛】队列和 queue
- 前言
- [1. 队列的概念](#1. 队列的概念)
- [2. 队列的模拟实现](#2. 队列的模拟实现)
- [3. queue](#3. queue)
-
- [3.1 创建](#3.1 创建)
- [3.2 size / empty](#3.2 size / empty)
- [3.3 push / pop](#3.3 push / pop)
- [3.4 front / back](#3.4 front / back)
- [3.5 测试代码](#3.5 测试代码)
- [4. 双端队列](#4. 双端队列)
- [5. deque](#5. deque)
-
- [5.1 创建](#5.1 创建)
- [5.2 size / empty](#5.2 size / empty)
- [5.3 push_front / push_back](#5.3 push_front / push_back)
- [5.4 front / back](#5.4 front / back)
- [5.6 clear](#5.6 clear)
- [5.7 测试代码](#5.7 测试代码)
- [6. 练习](#6. 练习)
- 结语
前言
队列是计算机科学中一种基础且重要的数据结构,遵循先进先出(FIFO)的原则,广泛应用于算法竞赛、操作系统调度、网络通信等领域。掌握队列及其变种(如双端队列)的实现与应用,能够帮助解决许多实际问题,例如广度优先搜索(BFS)、滑动窗口优化等。
本内容从队列的基本概念出发,逐步介绍如何通过数组或链表模拟队列的常见操作,包括入队、出队、访问队首队尾等。同时,结合 C++ STL 中的 queue 和 deque 容器,对比手动实现的差异,展示标准库的高效性与便捷性。最后通过练习题目巩固知识点,提升对队列灵活运用的能力。
无论是初学者还是有一定经验的选手,都能通过本内容系统理解队列的核心思想,并熟练应用于竞赛编程中。
1. 队列的概念
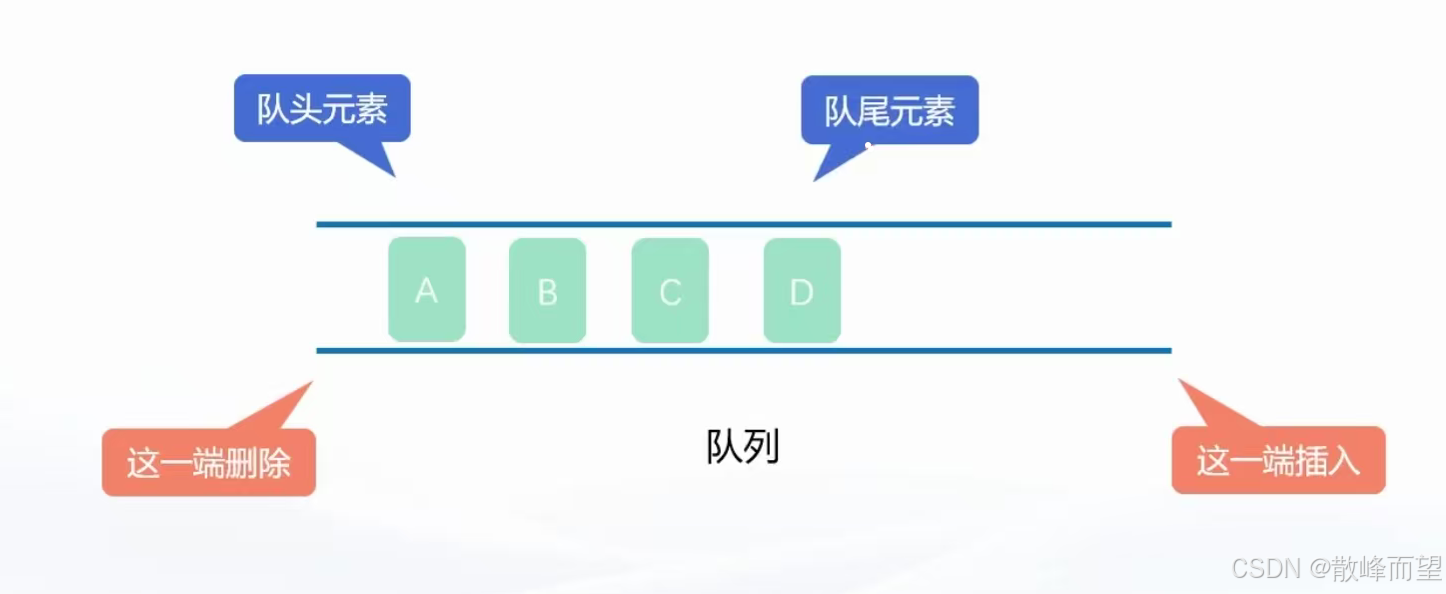
队列也是一种访问受限的线性表 ,它只允许在表的一端进行插入 操作,在另一端进行删除操作。
允许插入的一端称为队尾 ,允许删除的一端称为队头。
先进入队列的元素会先出队,故队列具有先进先出的特性,类似于食堂打饭的特点,先排队的人先有饭吃(不插队情况下)。

当队列中没有元素时,被称为空队 ,同时元素在队列里进出被称为入队 和出队。

这就是空队的情况。

一头插入一头删除。
2. 队列的模拟实现
2.1 创建
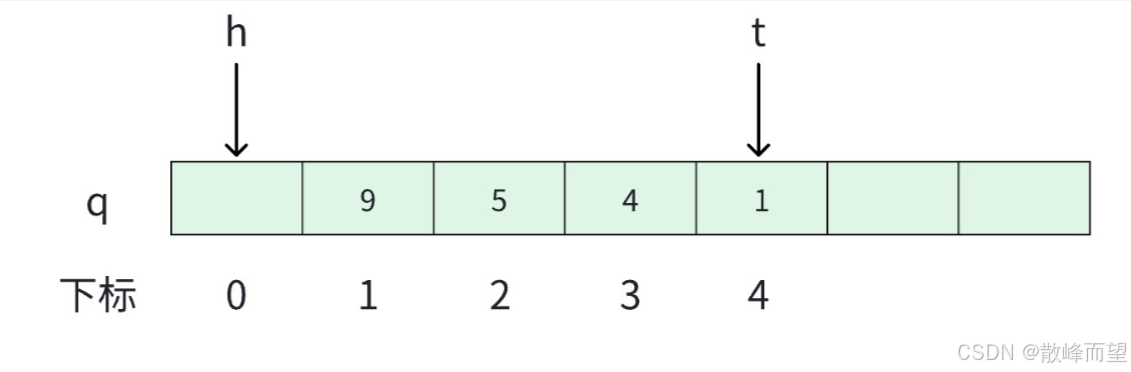
- 一个足够大的数组充当队列;
- 一个变量 h 标记队头元素的前一个位置;
- 一个变量 t 标记队尾元素的位置。
两个变量 (h, t] 是一种左开右闭的形式,这样设定纯属个人喜好,因为后续的代码写着比较舒服。
当然,也可以 h 标记队头元素的位置。只要能控制住代码不出现 bug,想怎么实现就怎么实现。
cpp
const int N = 1e6 + 10;
int h, t; // 队头指针,队尾指针
int q[N]; // 队列2.2 入队
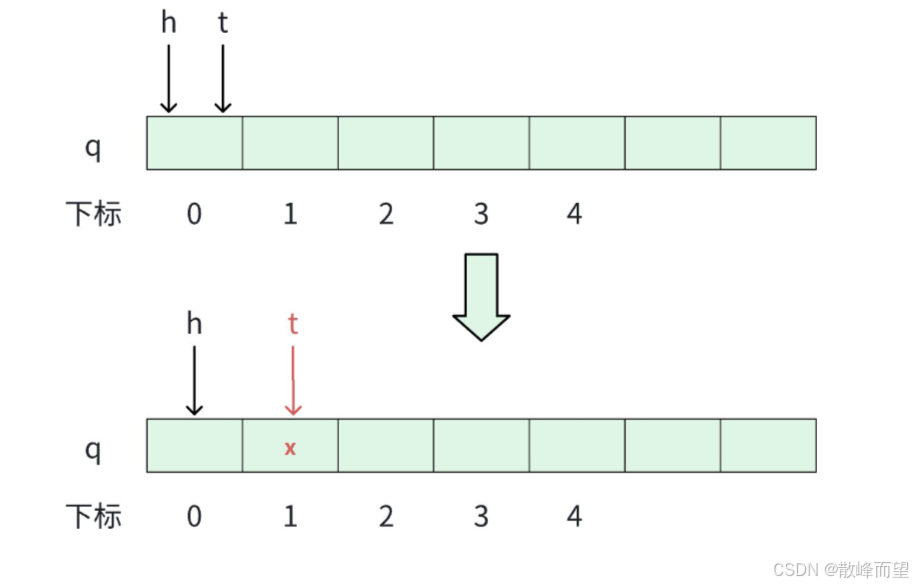
将 x 这个元素放入到队列中。
注意,我们这里依旧从下标为 1 的位置开始存储有效元素。
cpp
// 入队
void push(int x)
{
q[++t] = x;
}时间复杂度:O(1)
2.3 出队
即删除头元素。

cpp
// 出队
void pop()
{
h++;
}(入队出队代码 bug 都是和顺序表里面讲的一样的【顺序表】,一般自己判断一下即可)
时间复杂度:O(1)
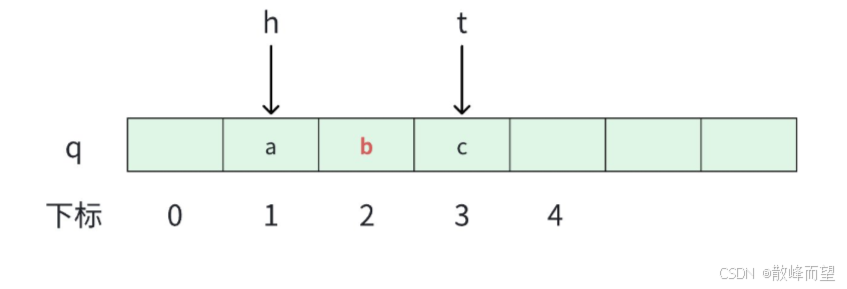
2.4 队头
返回队列里面的第一个元素。
cpp
// 队头元素
int front()
{
return q[h + 1];
}时间复杂度:O(1)
2.5 队尾
返回队列里面的最后一个元素
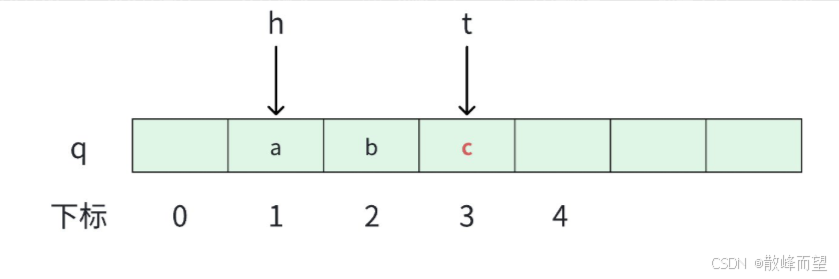
cpp
// 队尾元素
int back()
{
return q[t];
}时间复杂度:O(1)
2.6判空
判断队列是否为空。
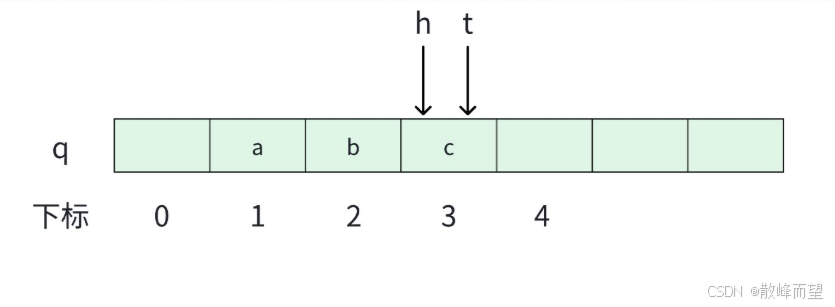
cpp
// 队列是否为空
bool empty()
{
return t == h;
}时间复杂度:O(1)
2.7元素个数
返回队列里面元素的个数。
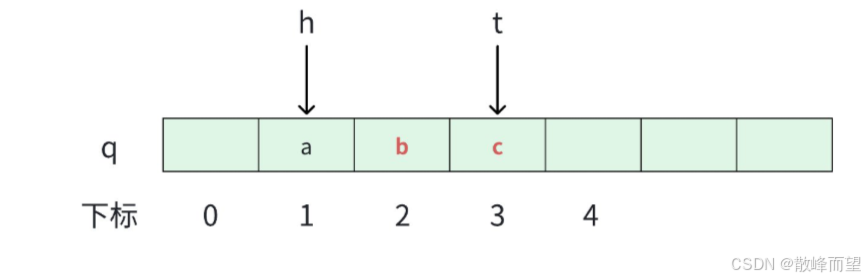
cpp
// 队列的大小
int size()
{
return t - h;
}时间复杂度:O(1)
2.8 测试代码
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
// 创建
int q[N], h, t;
// 入队
void push(int x)
{
q[++t] = x;
}
// 出队
void pop()
{
h++;
}
// 查询队头元素
int front()
{
return q[h + 1];
}
// 查询队尾元素
int back()
{
return q[t];
}
// 判断是否为空
bool empty()
{
return h == t;
}
// 有效元素的个数
int size()
{
return t - h;
}
int main()
{
// 测试
for(int i = 1; i <= 10; i++)
{
push(i);
}
while(size()) // while(!empty())
{
cout << front() << " " << back() << endl;
pop();
}
return 0;
}运行演示结果:
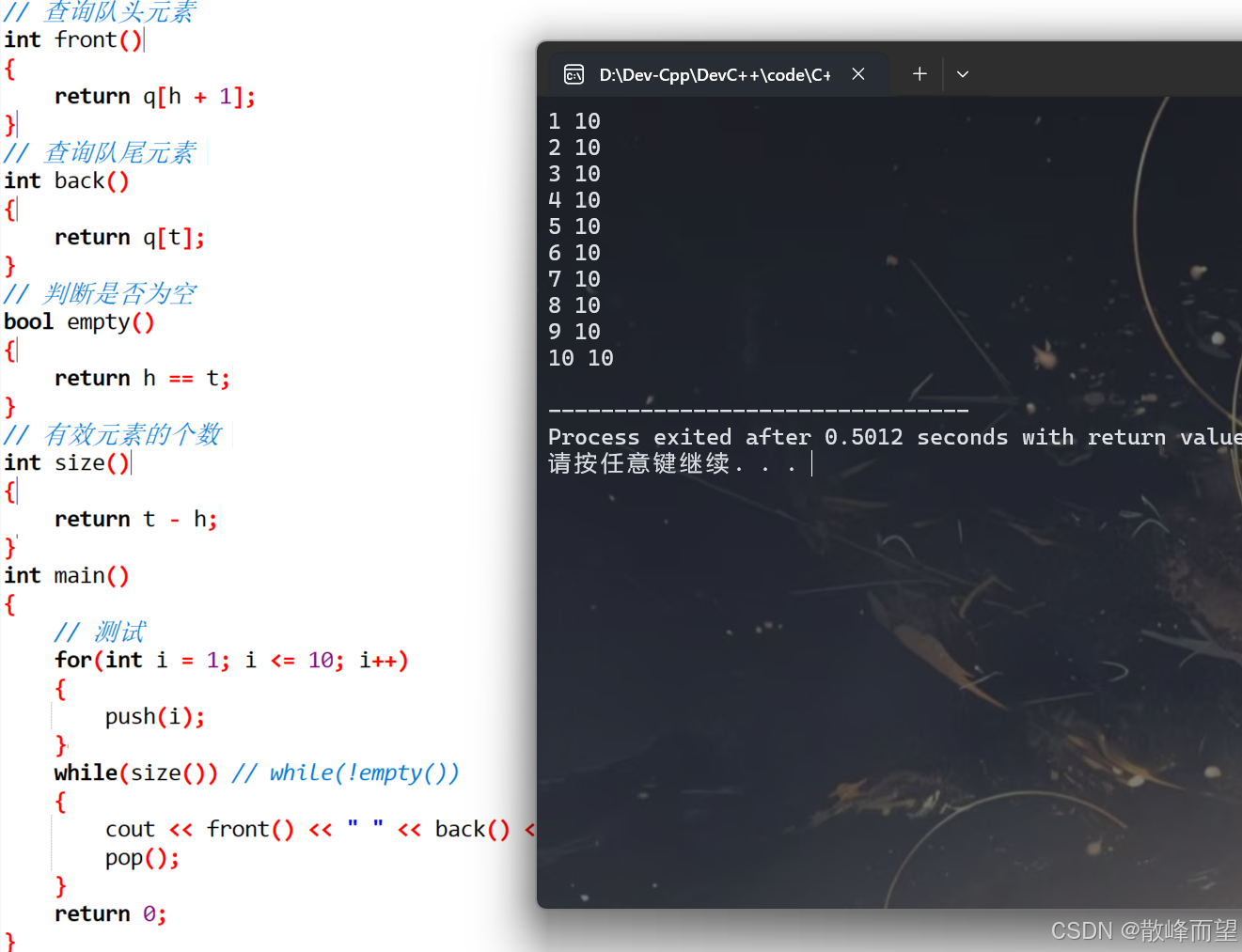
3. queue
依旧注意三点:
- 如何创建?
- 里面提供了什么函数?
- 每个函数的功能以及时间复杂度。
3.1 创建
queue<T> q;
T 可以是任意类型的数据。
3.2 size / empty
- size:返回队列里实际元素的个数;
- empty:返回队列是否为空。
时间复杂度:O(1)
3.3 push / pop
- push:入队;
- pop:出队。
时间复杂度:O(1)
3.4 front / back
- front:返回队头元素,但不会删除;
- back:返回队尾元素,但不会删除。
时间复杂度:O(1)
3.5 测试代码
cpp
#include <iostream>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
int main()
{
// 测试 queue
queue<PII> q;
for(int i = 1; i <= 10; i++)
{
q.push({i, i * 10});
}
while(q.size()) // while(!q.empty())
{
auto t = q.front();
q.pop();
cout << t.first << " " << t.second << endl;
}
return 0;
} 运行演示结果:

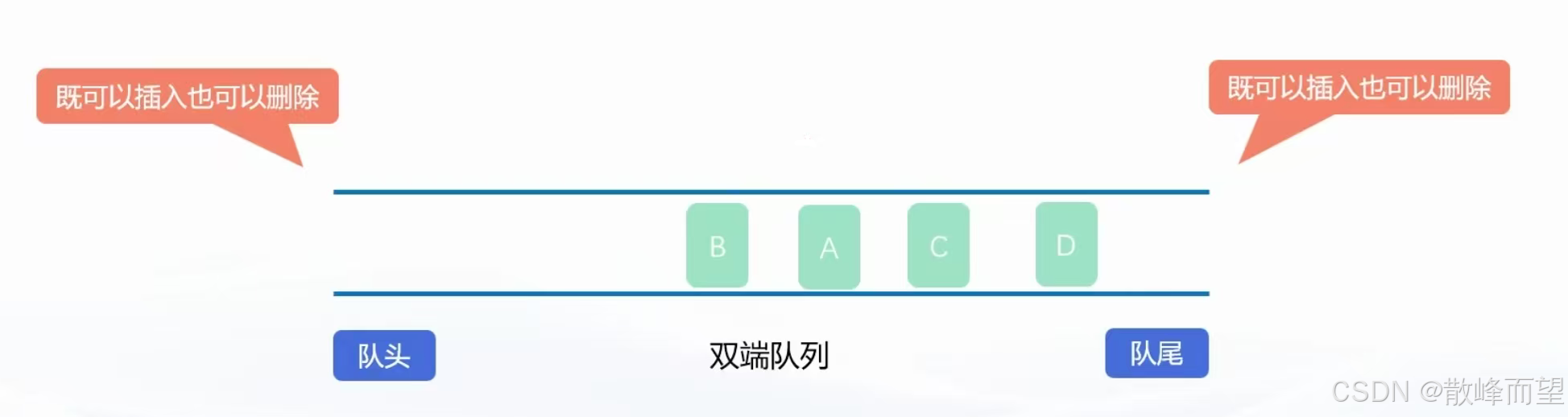
4. 双端队列
双端队列也是一种特殊线性结构,其允许两端都可以进行数据元素入队和出队操作。

将队列的两端分别称为前端和后端,两端都可以进行数据入队和出队。
5. deque
5.1 创建
deque<T> q;
T 可以是任意类型的数据。
5.2 size / empty
- size:返回队列里实际元素的个数;
- empty:返回队列是否为空。
时间复杂度:O(1)
5.3 push_front / push_back
- push_front:头插;
- push_back:尾插。
时间复杂度:O(1)
5.4 front / back
- front:返回队头元素,但不会删除;
- back:返回队尾元素,但不会删除。
时间复杂度:O(1)
5.6 clear
clear:清空队列。
时间复杂度:O(N)
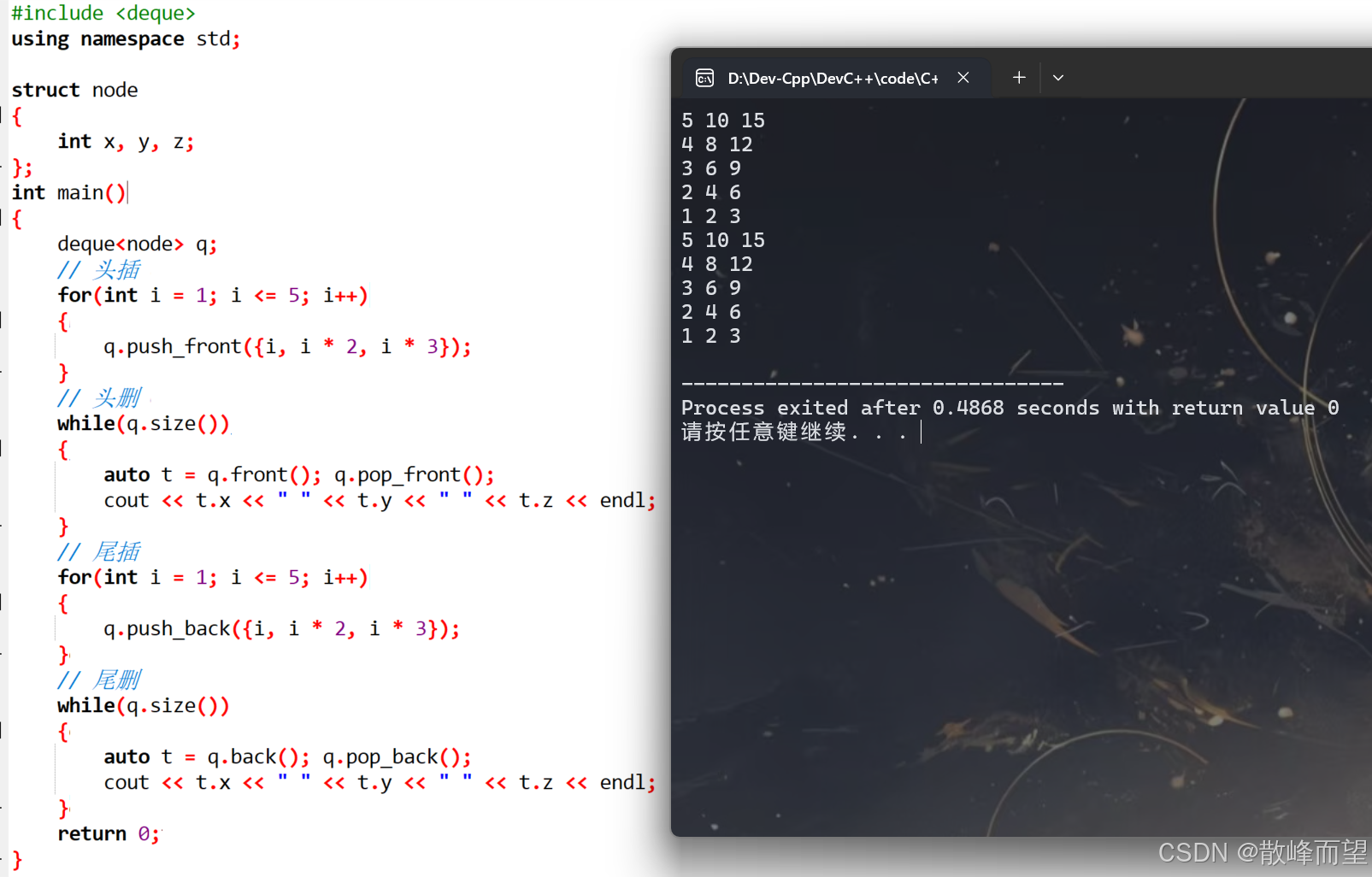
5.7 测试代码
cpp
#include <iostream>
#include <deque>
using namespace std;
struct node
{
int x, y, z;
};
int main()
{
deque<node> q;
// 头插
for(int i = 1; i <= 5; i++)
{
q.push_front({i, i * 2, i * 3});
}
// 头删
while(q.size())
{
auto t = q.front(); q.pop_front();
cout << t.x << " " << t.y << " " << t.z << endl;
}
// 尾插
for(int i = 1; i <= 5; i++)
{
q.push_back({i, i * 2, i * 3});
}
// 尾删
while(q.size())
{
auto t = q.back(); q.pop_back();
cout << t.x << " " << t.y << " " << t.z << endl;
}
return 0;
}运行演示结果:
6. 练习
结语
队列作为基础数据结构,遵循先进先出(FIFO)原则,在广度优先搜索(BFS)、任务调度等场景中广泛应用。通过模拟实现和标准库 queue 的对比,可以更深入理解其核心操作(入队、出队、访问队首/队尾)的底层逻辑。
愿诸君能一起共渡重重浪,终见缛彩遥分地,繁光远缀天。
