目录

1.摘要
本文研究多无人机协同农药喷洒中的最优任务分配问题(OSTAP),针对多无人机作业中存在的机型差异、田块边界不规则、喷雾漂移和操作水平差异等因素,本文建立了异构多无人机植保系统数学模型,并提出OSTAP。为求解该问题,研究将其转化为等价的组合优化问题,提出顺序无关枚举算法(OIES),在时间与空间复杂度上更高效,并与ETA、STA、DPSO及全排列算法进行对比。
2.问题陈述和数学建模
多无人机植保喷洒可提升作业效率,但由于无人机异构性(电量、载药量、喷幅、速度不同)、地块边界复杂、喷雾漂移与航迹重叠、以及操作员熟练度差异等因素,多机任务分配比一般同质多智能体系统更复杂。本文聚焦于高层任务规划与协同调度,不讨论漂移统计与喷洒参数优化,假设漂移影响范围可预测且无人机满足喷洒要求。
在假设地块喷洒需求均匀、系统无碰撞、单次飞行可完成分配任务等前提下,将面积为 S S S 的地块划分为 n n n个子区域 A = { a j } A=\{a_j\} A={aj},并把喷洒任务分配看作无人机集合 U = { u i } U=\left\{u_i\right\} U={ui}到子区域集合的映射 ϕ : u i ↦ a j \phi:u_i\mapsto a_j ϕ:ui↦aj,通常 k ≤ n k\leq n k≤n ,即单架 UAV 可能承担多个子任务。
无人机作业能力由电量与药量共同限制,其最大预计作业时间为:
T e i = min ( P i p i , C i c i ) T_{e_i}=\min\left(\frac{P_i}{p_i},\frac{C_i}{c_i}\right) Tei=min(piPi,ciCi)
考虑喷洒漂移与重叠,定义有效喷幅:
W i = ( 1 + m ) W s − W o W_i=(1+m)W_s-W_o Wi=(1+m)Ws−Wo
最优喷洒任务分配问题(OSTAP)目标是在满足覆盖与边界约束条件下,优化区域划分+任务分配:
{ t ^ a = min ( ⋃ i k ( t i j p = ⋃ j ( a j / v i ∣ u i ) ) ) n ^ p = min n s ^ r = min ( ∑ i , j ( S j ∣ u i − a j ) ) \begin{cases}\widehat{\mathbf{t}}a=\min\left(\bigcup_i^k\left(\mathbf{t}{ij}^p=\bigcup_j\left(\mathbf{a}_j\left/\mathbf{v}i\right|{u_i}\right)\right)\right)\\\widehat{\mathbf{n}}_p=\min n\\\widehat{\mathbf{s}}r=\min\left(\sum{i,j}\left(\mathbf{S}j|{u_i}-\mathbf{a}_j\right)\right)&\end{cases} ⎩ ⎨ ⎧t a=min(⋃ik(tijp=⋃j(aj/vi∣ui)))n p=minns r=min(∑i,j(Sj∣ui−aj))
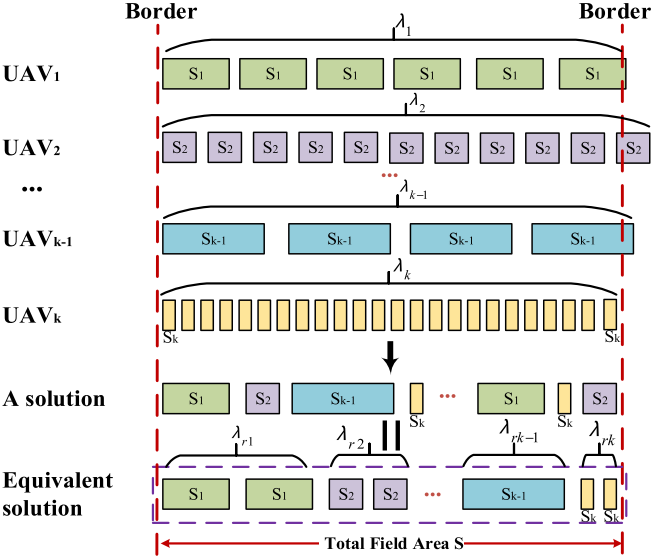
OSTAP将每架无人机一次作业视为可重复的作业单元(包含喷洒时间与固定准备/补给时间),多机协同完成任务等价于从这些作业单元中选取若干次组合,使覆盖面积达到整块地并使总耗时最小。由于解对执行顺序不敏感,采用全排列穷举虽能求最优,但复杂度极高且冗余严重,随着无人机数量增加难以在有限时间内求解。
3.与顺序无关的枚举解
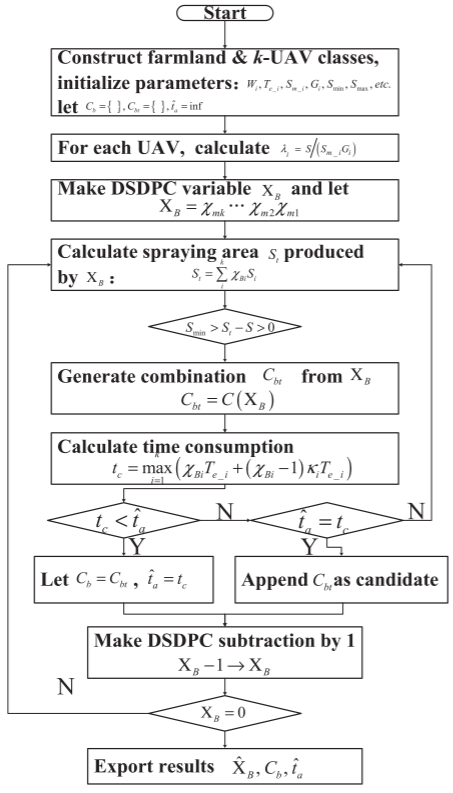
顺序无关枚举算法(OIES)将多无人机任务分配视为各无人机执行若干次周期作业的组合问题,并利用不同位不同进制计数规则(DSDPC)枚举所有可能的作业次数组合,避免对执行顺序进行全排列,从而消除大量冗余计算。OIES 通过依次生成组合、筛选满足覆盖面积约束的可行解,并计算其整体完成时间,持续更新最优结果。
ETA算法
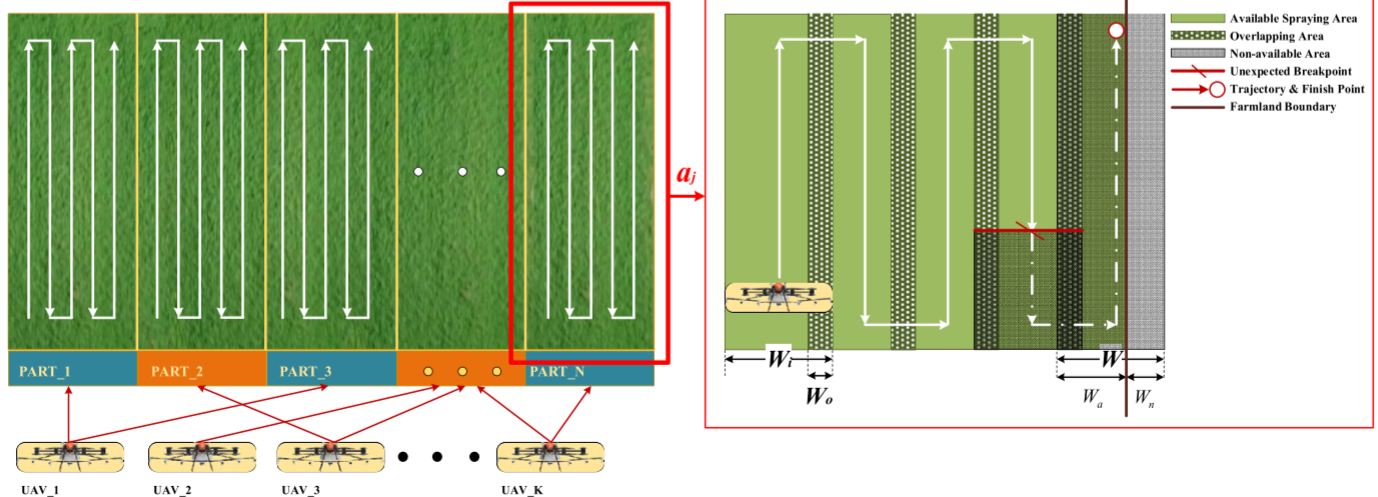
ETA(等任务分配)算法将地块平均划分给各 UAV,实现简单、计算开销低,但未考虑效率与精度,难以得到最优调度。其问题包括:分区可能超过单机作业能力导致作业中断;末次喷洒易产生越界喷洒和不可用面积;忽略无人机性能、操作熟练度及区域差异。因此,ETA 仅适用于快速粗略分配,不适合异构多无人机的高效植保作业。
STA算法
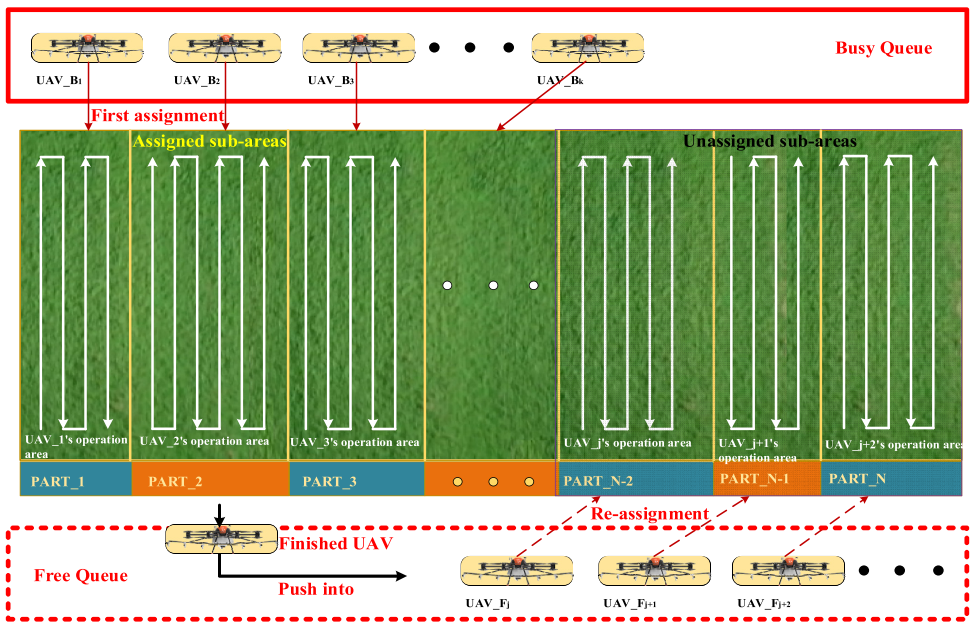
STA(顺序任务分配)算法依据单架 UAV 的最大作业能力进行分区,并按顺序将空闲 UAV 分配给未完成区域,能够充分利用每架无人机的作业能力。通过忙碌---空闲队列调度,STA 可连续推进喷洒任务直至完成。但其顺序分配仍可能造成时间浪费并增加额外飞行次数,整体效率仍有限。
DPSO算法
DPSO将每个粒子视为一个潜在任务分配方案,通过个体经验与群体信息共享不断逼近最优解。相比传统 PSO,DPSO 在粒子编码和更新规则上适配离散空间,并通过整数映射实现搜索:
{ v φ D P S O ( k + 1 ) = c 1 D P S O × v φ D P S O ( k ) + c 2 D P S O ( P D P S O D P S O ( k ) − p φ D P S O ( k ) ) + c 3 D P S O ( P g b e s t D P S O ( k ) − p φ D P S O ( k ) ) p φ D P S O ( k + 1 ) = p φ D P S O ( k ) + v φ D P S O ( k + 1 ) \begin{cases}v_{\varphi}^{\mathrm{DPSO}}(k+1)=c_{1}^{\mathrm{DPSO}}\times v_{\varphi}^{\mathrm{DPSO}}(k)+c_{2}^{\mathrm{DPSO}}(P_{\mathrm{DPSO}}^{\mathrm{DPSO}}(k)-p_{\varphi}^{\mathrm{DPSO}}(k))+c_{3}^{\mathrm{DPSO}}\left(P_{\mathrm{gbest}}^{\mathrm{DPSO}}(k)-p_{\varphi}^{\mathrm{DPSO}}(k)\right)\\p_{\varphi}^{\mathrm{DPSO}}(k+1)=p_{\varphi}^{\mathrm{DPSO}}(k)+v_{\varphi}^{\mathrm{DPSO}}(k+1)&\end{cases} {vφDPSO(k+1)=c1DPSO×vφDPSO(k)+c2DPSO(PDPSODPSO(k)−pφDPSO(k))+c3DPSO(PgbestDPSO(k)−pφDPSO(k))pφDPSO(k+1)=pφDPSO(k)+vφDPSO(k+1)
4.结果展示
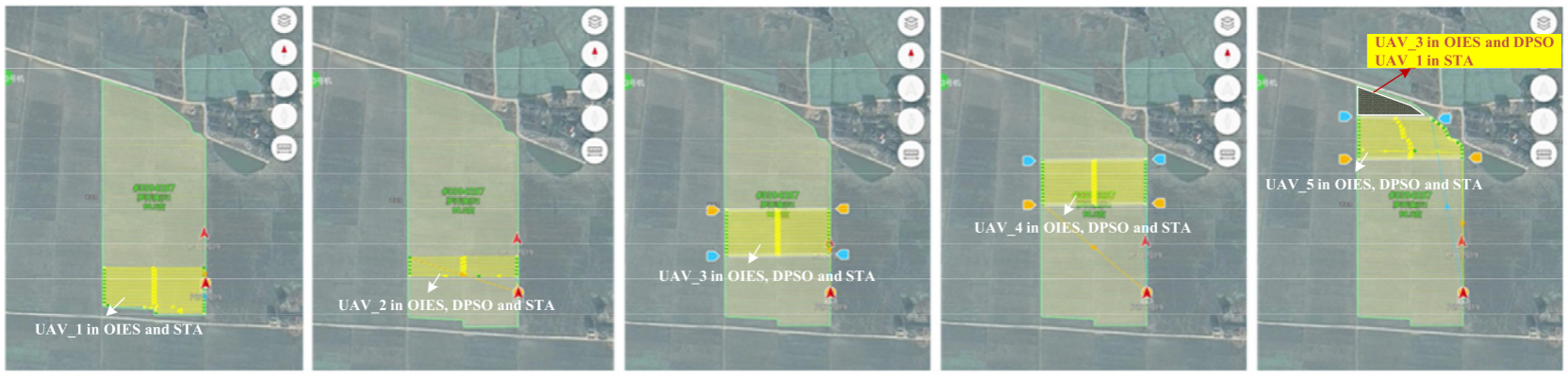
5.参考文献
1\] Li Y, Xu Y, Xue X, et al. Optimal spraying task assignment problem in crop protection with multi-UAV systems and its order irrelevant enumeration solution\[J\]. Biosystems Engineering, 2022, 214: 177-192. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx