文章目录
- [一. 力扣 [面试题 08.06. 汉诺塔问题](https://leetcode.cn/problems/hanota-lcci/description/)](#一. 力扣 面试题 08.06. 汉诺塔问题)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [二. 力扣 [21. 合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)](#二. 力扣 21. 合并两个有序链表)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [三. 力扣 [206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/description/)](#三. 力扣 206. 反转链表)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
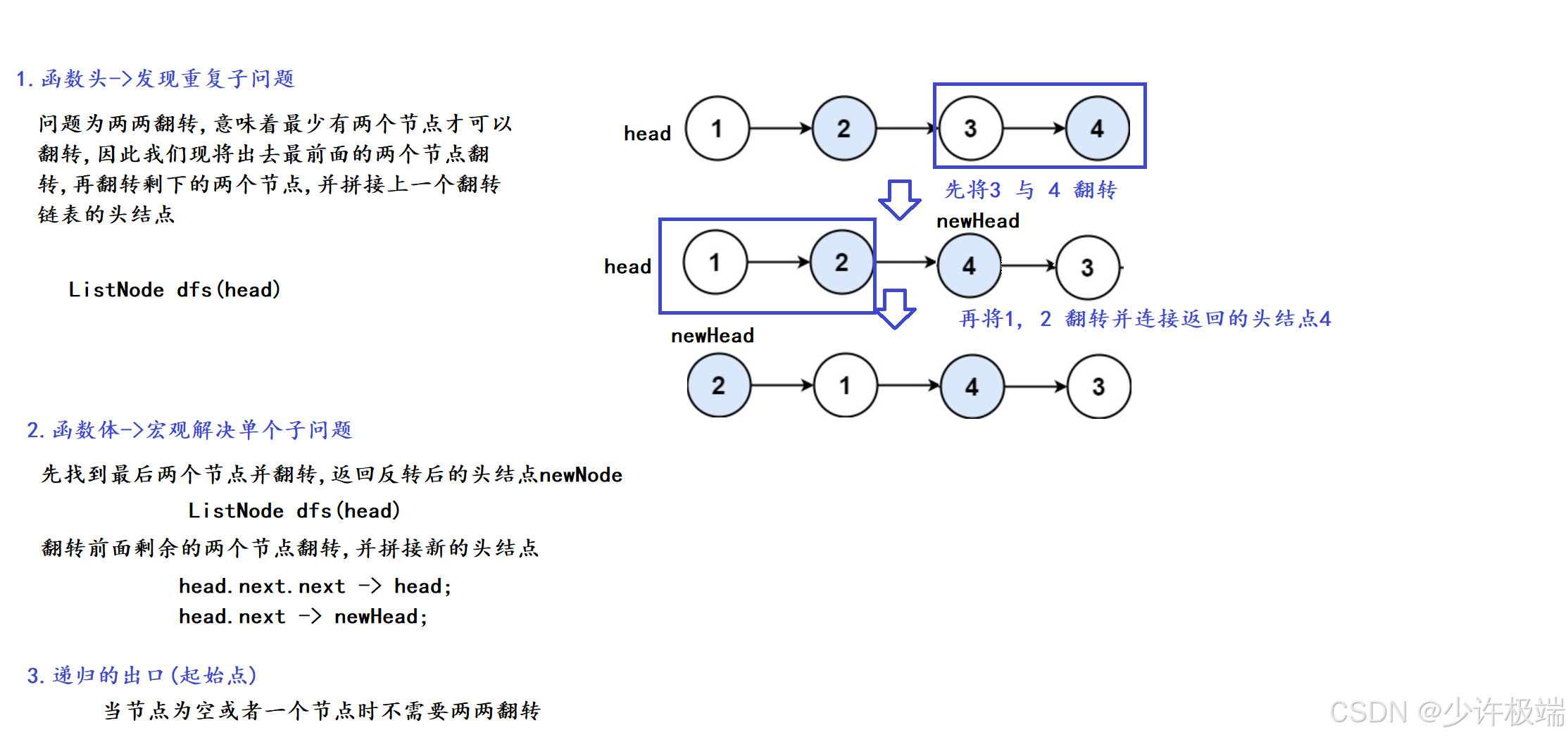
- [四. 力扣 [24. 两两交换链表中的节点](https://leetcode.cn/problems/swap-nodes-in-pairs/)](#四. 力扣 24. 两两交换链表中的节点)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [五. 力扣 [50. Pow(x, n)](https://leetcode.cn/problems/powx-n/description/)](#五. 力扣 50. Pow(x, n))
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
一. 力扣 面试题 08.06. 汉诺塔问题
1. 题目解析
我们大多数人接触的第一道递归题目应该就是汉诺塔, 当初给小编难的花了两天搞定, 现在再次看会有新的体会
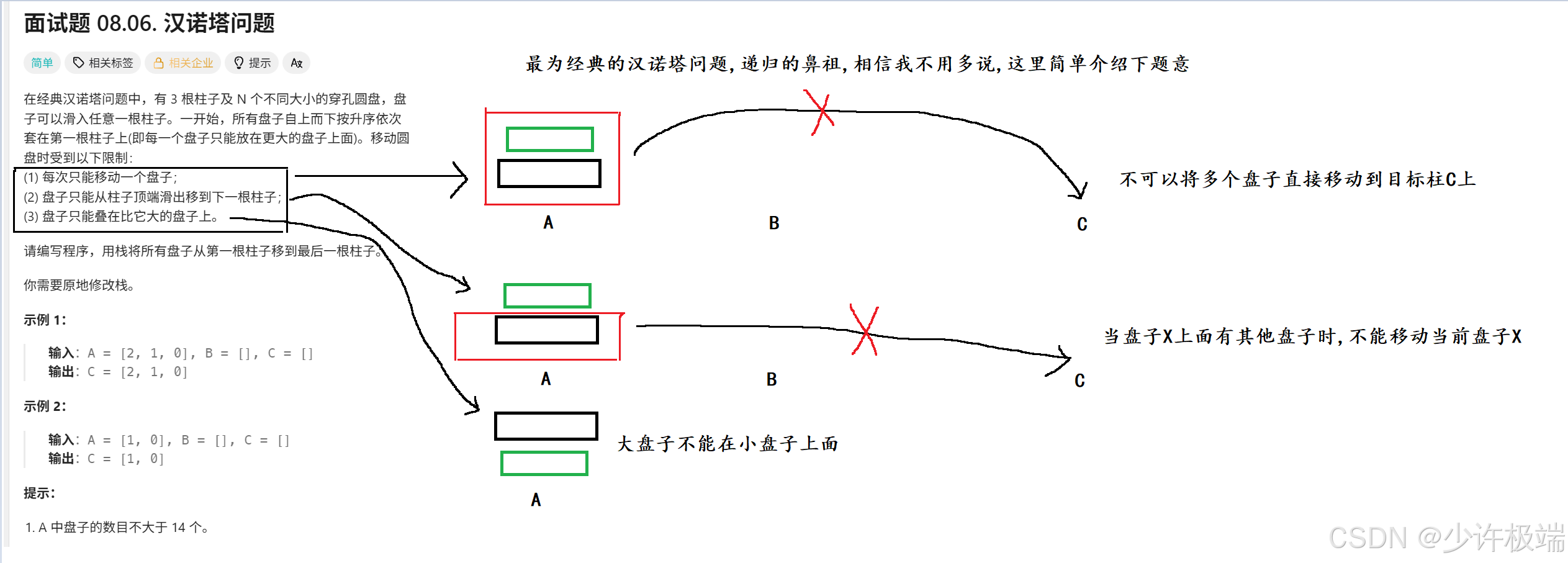
2. 算法原理
1. 当盘子数为1时, 可以直接放到目标盘子, 一步操作
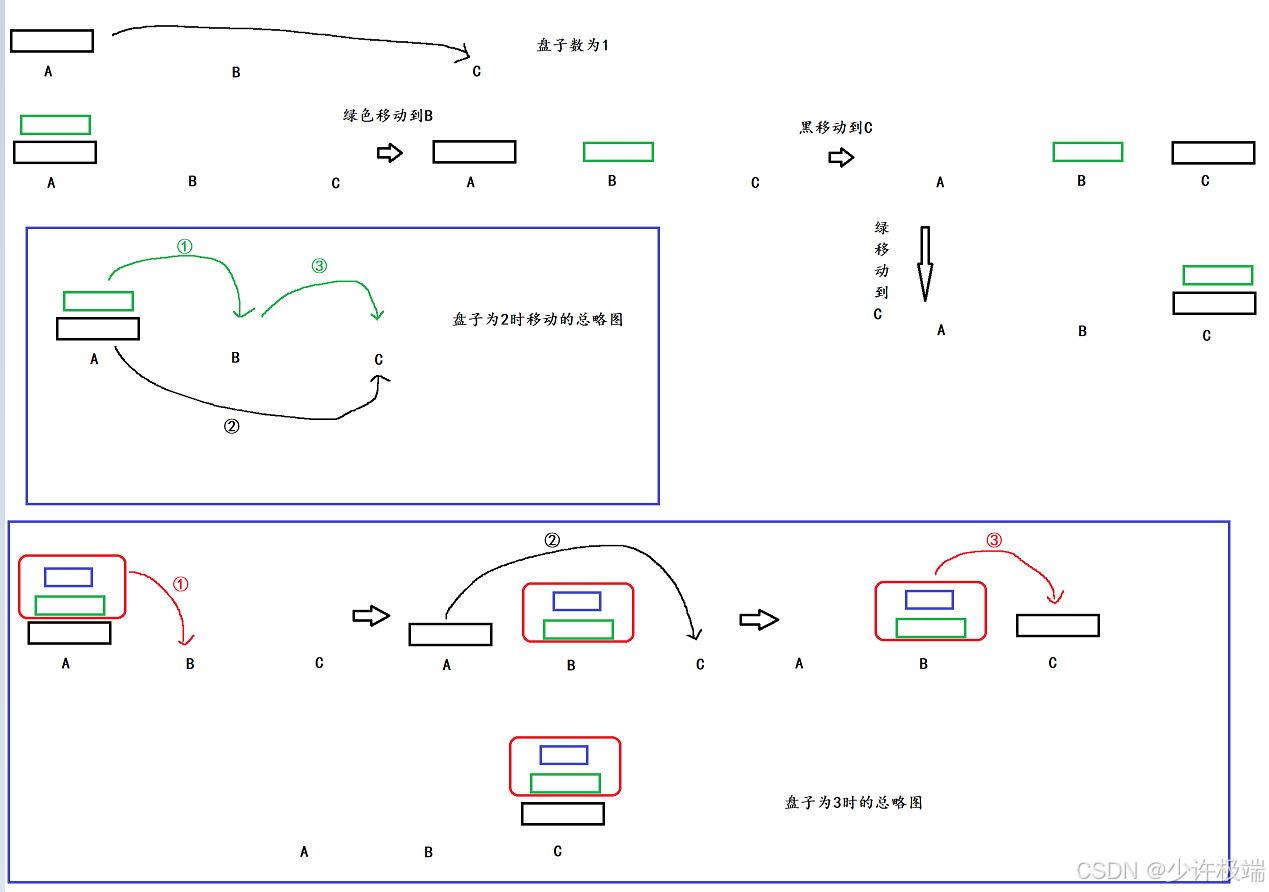
2. 当盘子数为2时, 小盘子先放在B, 大盘子放在C, 小盘子再放到C, 为三步操作
3. 当盘子数为3时, 将黑色上面的两个盘子看为一个整体, 步骤就简化为了:
第一步: 绿和蓝两个盘子从起始柱子A, 借助辅助柱子C, 移动到目标柱子B
第二步: 最大的盘子从起始柱子A, 直接移动到目标柱子C
第三步: 绿和蓝两个盘子从起始柱子B, 借助辅助柱子A, 移动到目标柱子C
因此3个盘子也可以拆解为三步, 具体两个盘子由辅助柱子移动到目标柱子的过程我们不用考虑, 假设方法一定可以完成我们的要求
4. 当盘子数为n时, 将最底下最大盘子上面的n-1个盘子看为一个整体X, 步骤简化为:
第一步: X从起始柱子A, 借助辅助柱子C, 移动到目标柱子B
第二步: 最大的盘子从起始柱子A, 直接移动到目标柱子C
第三步: X从起始柱子B, 借助辅助柱子A, 移动到目标柱子C
因此n个盘子也可以拆解为三步, 具体n-1个盘子由辅助柱子移动到目标柱子的过程我们不用考虑, 假设方法一定可以完成我们的要求
因此我们可以拆解出子问题->函数头: 一堆盘子n由起始柱子A, 借助辅助柱子B, 移动到目标柱子C -> dfs(n, A, B, C)
分解子问题, 解决一个子问题相当于解决了整个问题:
① n-1个盘子由A借助C移动到B: dfs(int n-1, A, C, B)
② 最大的盘子n由A移动到C: n -> C
③ n-1个盘子由B借助A移动到C: -> dfs(int n-1, B, A, C)
递归结束点(起始点): 2到n个盘子时, 都分为三个步骤, 但是1个盘子时, 就一步直接从起始柱移动到目标柱
3. 代码
java
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
int n = A.size();
dfs(n, A, B, C);
}
void dfs(int n, List<Integer> A, List<Integer> B, List<Integer> C) {
// 递归出口
if (n == 1) {
C.add(A.remove(A.size() - 1));
return;
}
// 第一步
dfs(n - 1, A, C, B);
// 第二步
C.add(A.remove(A.size() - 1));
// 第三步
dfs(n - 1, B, A, C);
}
}二. 力扣 21. 合并两个有序链表
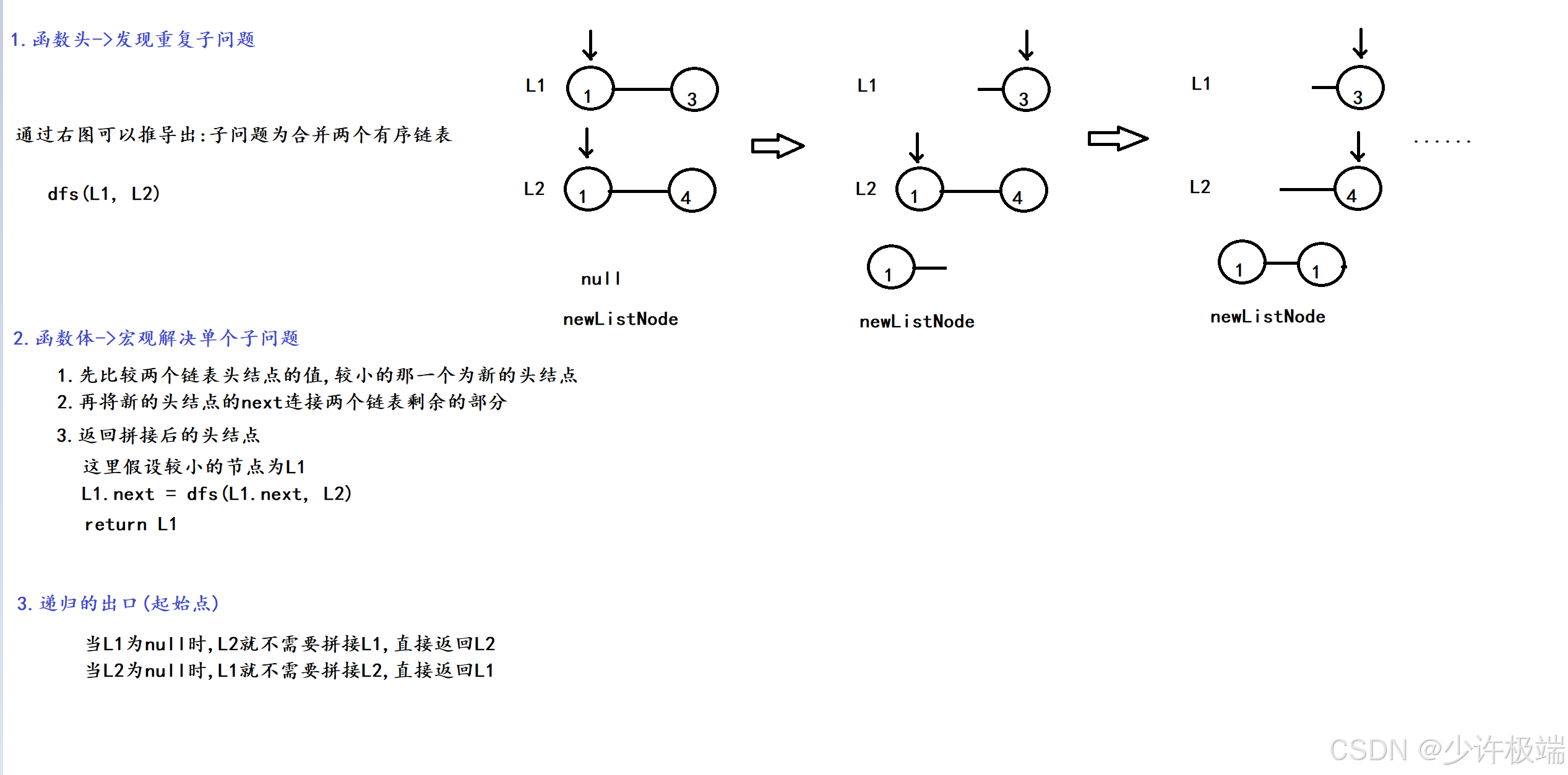
1. 题目解析
2. 算法原理
3. 代码
bash
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if (list1 == null) {
return list2;
}
if (list2 == null) {
return list1;
}
if (list1.val < list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
}else {
list2.next = mergeTwoLists(list1, list2.next);
return list2;
}
}
}三. 力扣 206. 反转链表
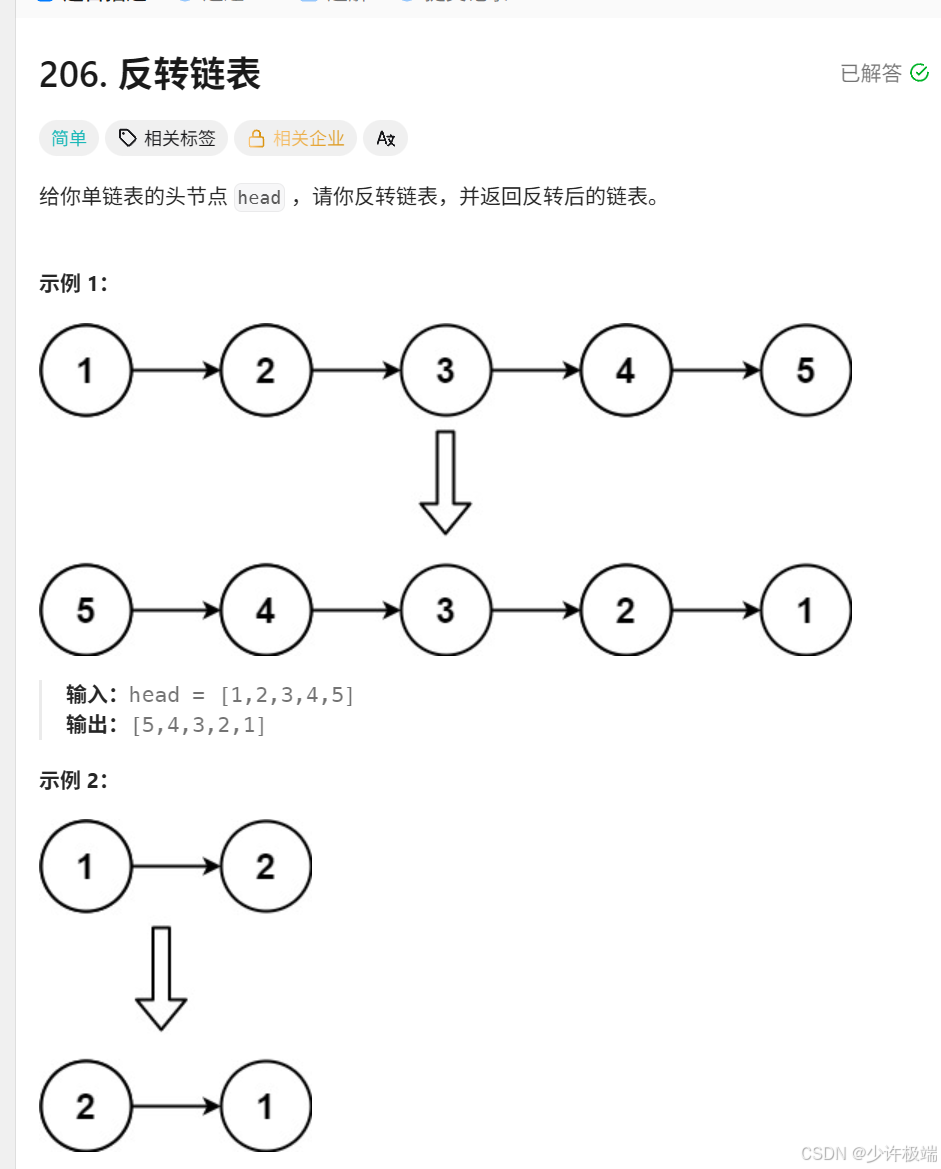
1. 题目解析
题意简单易懂, 这里不过多赘述
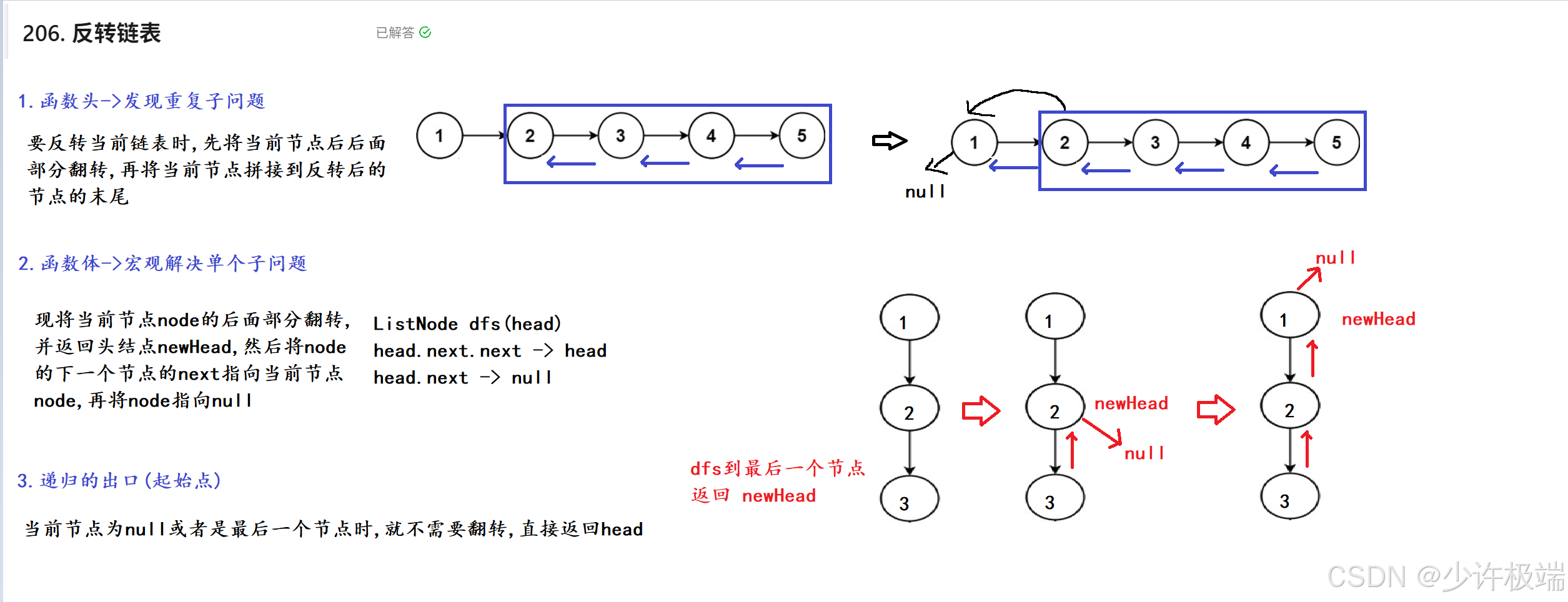
2. 算法原理
3. 代码
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}四. 力扣 24. 两两交换链表中的节点
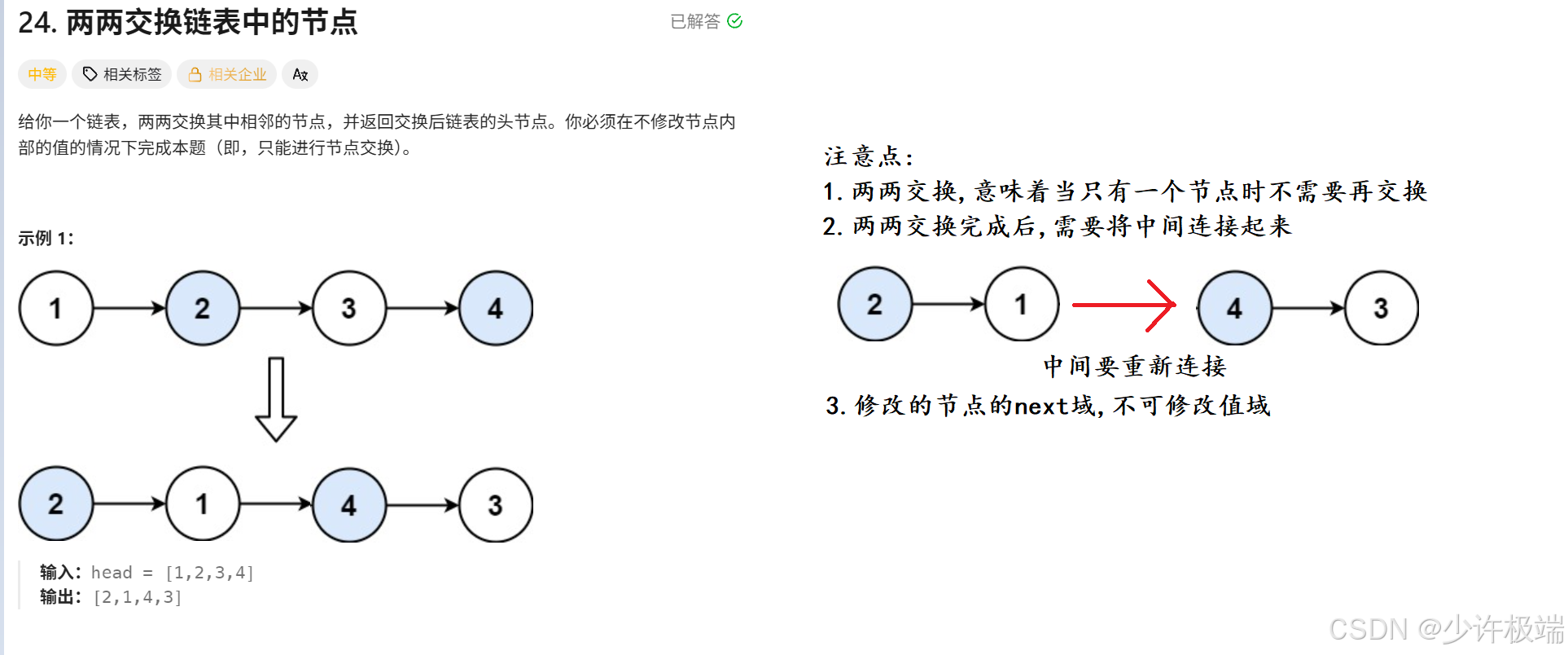
1. 题目解析
2. 算法原理
3. 代码
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = swapPairs(head.next.next);
ListNode tmp = head.next;
head.next.next = head;
head.next = newHead;
return tmp;
}
}五. 力扣 50. Pow(x, n)
1. 题目解析
实现标准库中的求次幂的方法
2. 算法原理
这里用快速幂算法
3. 代码
java
class Solution {
public double myPow(double x, int n) {
return n > 0 ? pow(x, n) : 1.0 / pow(x, -n);
}
public double pow(double x, int n) {
if (n == 0) {
return 1.0;
}
double tmp = myPow(x, n / 2);
if (n > 0) {
return n % 2 == 0 ? tmp * tmp : x * tmp * tmp;
}else {
return n % 2 == 0 ? 1.0 / (tmp * tmp) : 1.0 / (x * tmp * tmp);
}
}
}