leetcode回溯算法（77.组合）

回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了。

那么我把组合问题抽象为如下树形结构：

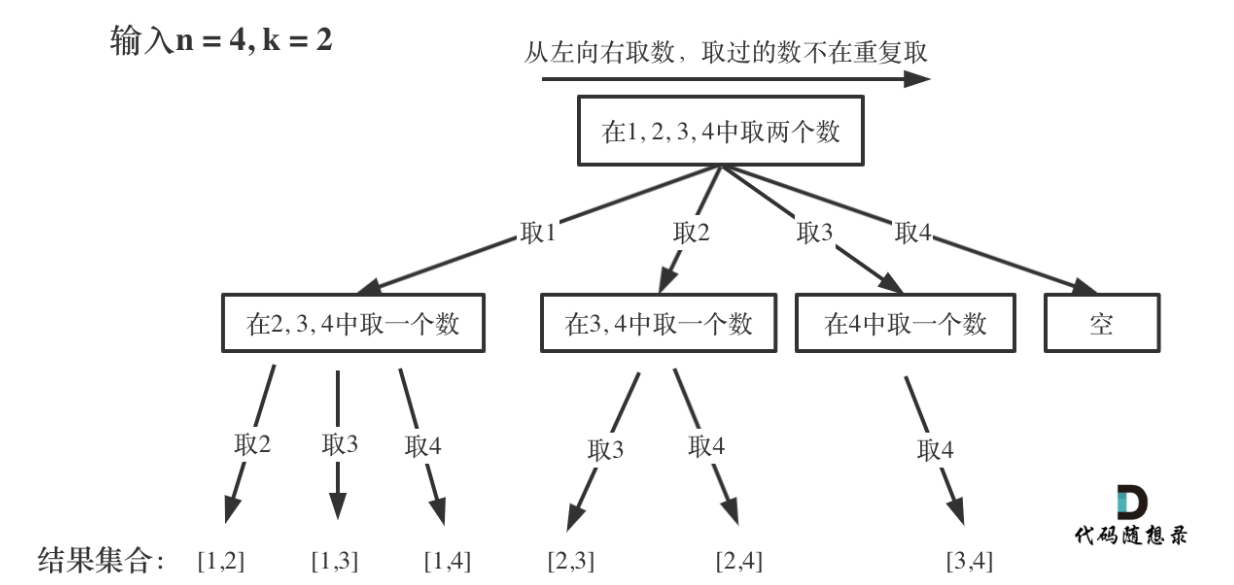
可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。

第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现n相当于树的宽度，k相当于树的深度。

回溯法三部曲

• 递归函数的返回值以及参数

在这里要定义两个全局变量，一个用来存放符合条件单一结果，一个用来存放符合条件结果的集合。

vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果

其实不定义这两个全局变量也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性。

需要startIndex来记录下一层递归，搜索的起始位置。

vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件单一结果
void backtracking(int n, int k, int startIndex)

• 回溯函数终止条件

什么时候到达所谓的叶子节点了呢？

path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。

此时用result二维数组，把path保存起来，并终止本层递归。

if (path.size() == k) {
    result.push_back(path);
    return;
}

• 单层搜索的过程

回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

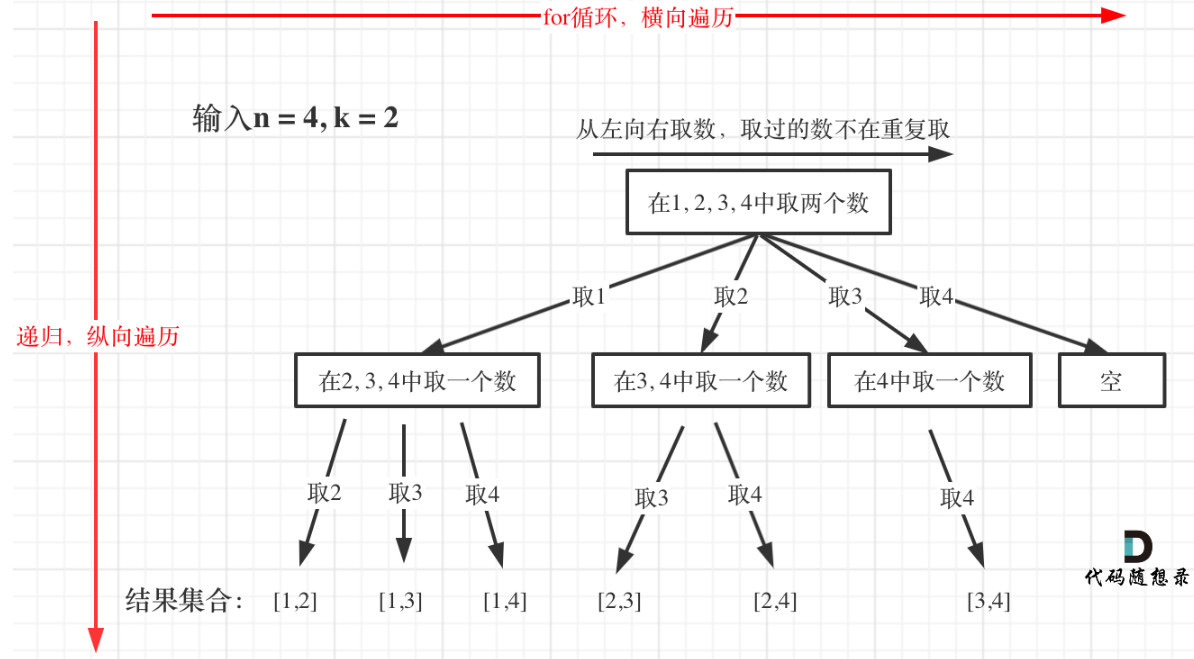
for循环每次从startIndex开始遍历，然后用path保存取到的节点i。

for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
    path.push_back(i); // 处理节点
    backtracking(n, k, i + 1); // 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
    path.pop_back(); // 回溯，撤销处理的节点
}

可以看出backtracking（递归函数）通过不断调用自己一直往深处遍历，总会遇到叶子节点，遇到了叶子节点就要返回。

backtracking的下面部分就是回溯的操作了，撤销本次处理的结果。

组合问题C++完整代码如下：

class Solution {
private:
    vector<vector<int>> result; // 存储所有组合结果的二维数组
    vector<int> path; // 存储当前组合的路径（单次组合结果）
    
    // 回溯函数
    // n: 数字范围1~n
    // k: 组合需要的数字个数
    // startIndex: 当前层开始遍历的起始数字
    void backtracking(int n, int k, int startIndex) {
        // 终止条件：当前路径已包含k个数字
        if (path.size() == k) {
            result.push_back(path); // 将当前组合加入结果集
            return; // 结束当前分支
        }
        
        // 遍历当前层的所有选择
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); // 将当前数字加入路径（做出选择）
            backtracking(n, k, i + 1); // 递归进入下一层，从i+1开始避免重复
            path.pop_back(); // 回溯，撤销选择，移除最后一个数字
        }
    }
    
public:
    // 主函数：生成所有组合
    // n: 数字范围1~n
    // k: 每个组合的数字个数
    vector<vector<int>> combine(int n, int k) {
        result.clear(); // 清空结果集（保证多次调用时结果独立）
        path.clear();   // 清空当前路径
        backtracking(n, k, 1); // 从数字1开始回溯
        return result; // 返回所有组合结果
    }
};

核心思路注释：

1. 回溯法（Backtracking）：通过递归尝试所有可能的选择，当发现当前路径不满足条件时回退到上一步

2. 剪枝 ：每次递归从i+1开始，避免重复使用数字（组合不考虑顺序）

3. 终止条件：当路径长度等于k时，说明找到了一个有效组合

回溯法模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

我们以 n=4, k=2 为例来模拟这个代码的执行过程。我们要从数字 [1,2,3,4] 中选出所有 2 个数的组合。

初始调用

combine(4, 2) {
  result = []
  path = []
  backtracking(4, 2, 1)  }

第一层递归：backtracking(4, 2, 1)

for i = 1 to 4:
  // 第一次循环：i = 1
  path.push_back(1) → path = [1]
  backtracking(4, 2, 2)  // 进入第二层

第二层递归：backtracking(4, 2, 2)

此时 path = [1], size = 1 ≠ k(2)，继续执行
for i = 2 to 4:
  // 第一次循环：i = 2
  path.push_back(2) → path = [1,2]
  backtracking(4, 2, 3)  // 进入第三层

第三层递归：backtracking(4, 2, 3)

此时 path = [1,2], size = 2 == k
→ 满足终止条件
result.push_back([1,2]) → result = [[1,2]]
return  // 返回到第二层

回到第二层（继续执行）

path.pop_back() → path = [1]  // 回溯，移除2
// 继续for循环：i = 3
path.push_back(3) → path = [1,3]
backtracking(4, 2, 4)  // 进入第三层

第三层递归：backtracking(4, 2, 4)

此时 path = [1,3], size = 2 == k(2)
result.push_back([1,3]) → result = [[1,2], [1,3]]
return // 第二层

回到第二层（继续执行）

path.pop_back() → path = [1]
// 继续for循环：i = 4
path.push_back(4) → path = [1,4]
backtracking(4, 2, 5)  // 进入第三层

.........

.........

.........

.........

容器类型	添加元素	移除元素	特点
vector	push_back()	pop_back()	动态数组，支持随机访问
deque	push_back(), push_front()	pop_back(), pop_front()	双端队列
list	push_back(), push_front()	pop_back(), pop_front()	双向链表
stack	push()	pop()	后进先出（LIFO）
queue	push()	pop()	先进先出（FIFO）
priority_queue	push()	pop()	优先级队列