leetcode回溯算法（17.电话号码的字母组合）

数字和字母如何映射

定义一个二维数组

const string letterMap[10] = {
    "", // 0
    "", // 1
    "abc", // 2
    "def", // 3
    "ghi", // 4
    "jkl", // 5
    "mno", // 6
    "pqrs", // 7
    "tuv", // 8
    "wxyz", // 9
};

   // const 表示这个映射表是常量，不会被修改
   // 编译器可以优化，放在只读内存区

例如：输入："23"，抽象为树形结构，如图所示：

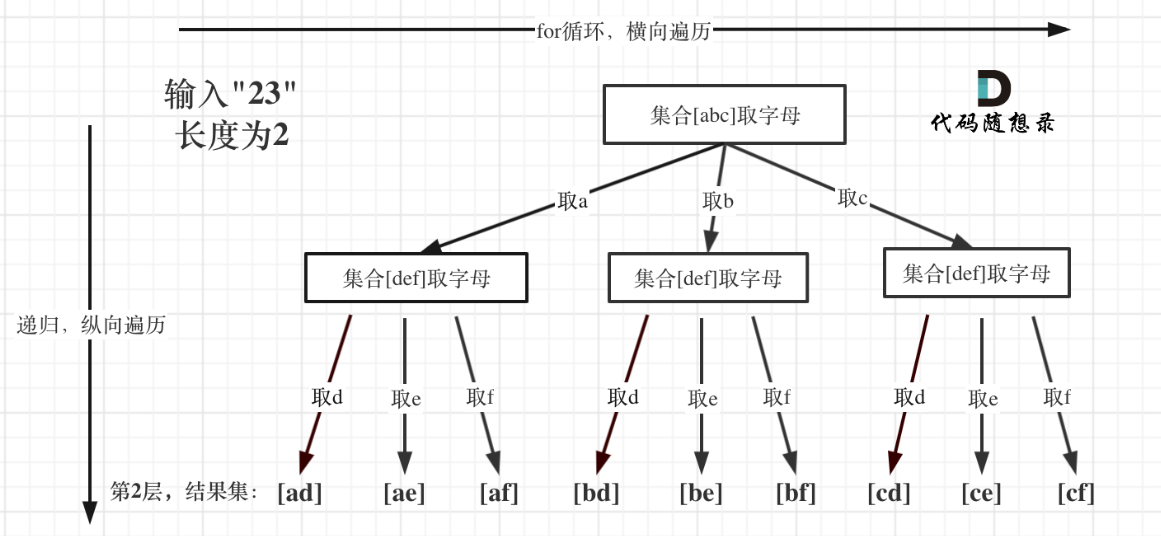
图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。

回溯三部曲：

• 确定回溯函数参数

首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。

再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。

这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。

vector<string> result;
string s;
void backtracking(const string& digits, int index)
// 使用const引用，避免拷贝，如果每次拷贝，会使性能变差

// 如果不使用&，而是每次要拷贝，会导致每次递归调用都会复制整个digits字符串
// 如果digits="23456789"，每次都要拷贝8个字符

• 确定终止条件

例如输入用例"23"，两个数字，那么根节点往下递归两层就可以了，叶子节点就是要收集的结果集。

那么终止条件就是如果index 等于 输入的数字个数（digits.size）了（本来index就是用来遍历digits的）。

然后收集结果，结束本层递归。

if (index == digits.size()) {
    result.push_back(s);
    return;
}

• 确定单层遍历逻辑

首先要取index指向的数字，并找到对应的字符集（手机键盘的字符集）。

然后for循环来处理这个字符集，代码如下：

int digit = digits[index] - '0';        // 将index指向的数字转为int
string letters = letterMap[digit];      // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
    s.push_back(letters[i]);            // 处理
    backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了
    s.pop_back();                       // 回溯
}

完整代码如下：

class Solution {
private:
    // 定义数字到字母的映射表，下标对应数字
    const string letterMap[10] = {
        "", // 0
        "", // 1
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
    };
public:
    vector<string> result; // 存储所有可能的字母组合结果
    string s; // 当前正在构建的字母组合字符串
    
    // 回溯函数
    void backtracking(const string& digits, int index) {
        // 终止条件：已经处理完所有数字
        if (index == digits.size()) {
            result.push_back(s); // 将当前组合加入结果集
            return;
        }
        
        int digit = digits[index] - '0'; // 将当前数字字符转为整数
        string letters = letterMap[digit]; // 获取当前数字对应的字母集合
        
        // 遍历当前数字对应的所有字母
        for (int i = 0; i < letters.size(); i++) {
            s.push_back(letters[i]); // 将当前字母加入组合
            backtracking(digits, index + 1); // 递归处理下一个数字
            s.pop_back(); // 回溯：移除最后加入的字母，尝试其他可能
        }
    }
    
    // 主函数：生成所有字母组合
    vector<string> letterCombinations(string digits) {
        s.clear(); // 清空当前组合字符串
        result.clear(); // 清空结果集
        
        // 边界情况：输入为空字符串
        if (digits.size() == 0) {
            return result; // 返回空结果
        }
        
        backtracking(digits, 0); // 从第0个数字开始回溯
        return result; // 返回所有组合结果
    }
};

举例：

以输入 digits = "23" 为例，模拟整个代码的流程。

初始状态

• digits = "23"

• result = []

• s = ""

1. 主函数letterCombinations("23")

• 输入不为空，继续执行

• 调用 backtracking("23", 0)

2. backtracking("23", 0) - 第一层递归

• index = 0，不等于 digits.size()（2），继续执行

• digit = digits[0] - '0' = '2' - '0' = 2

• letters = letterMap[2] = "abc"

• 进入 for 循环，遍历 "abc"

string letterMap[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
// 索引:        0    1     2      3      4      5      6       7      8       9
// 对应数字:    ""   ""   "abc"  "def"  "ghi"  "jkl"  "mno"  "pqrs"  "tuv"  "wxyz"

char digit = '2';
// digit = '2'，ASCII 码值为 50
// '0' 的 ASCII 码值为 48

int index = digit - '0';  // 50 - 48 = 2
string letters = letterMap[index];  // letterMap[2]

// letters 的值为 "abc"

当i = 0，letters[0] = 'a'

• s.push_back('a') → s = "a"

• 递归调用 backtracking("23", 1)

3. backtracking("23", 1) - 第二层递归

• index = 1，不等于 2，继续执行

• digit = digits[1] - '0' = '3' - '0' = 3

• letters = letterMap[3] = "def"

• 进入 for 循环，遍历 "def"

当 i = 0，letters[0] = 'd'

• s.push_back('d') → s = "ad"

• 递归调用 backtracking("23", 2)

4. backtracking("23", 2) - 第三层递归

• index = 2，等于 digits.size()（2）

• 满足终止条件：result.push_back(s) → result = ["ad"]

• 返回上一层（第二层递归）

回到第二层递归 backtracking("23", 1) 的 for 循环中

• s.pop_back() →（移除 'd'）所以现在 s = "a"

• i++ → 所以现在i = 1

当i = 1，letters[1] = 'e'

• s.push_back('e') → s = "ae"

• 递归调用 backtracking("23", 2)

backtracking("23", 2) - 第三层递归

• 满足终止条件：result.push_back(s) → result = ["ad", "ae"]

• 返回上一层

.........

.........

.........

.........

1. i=0 开始的循环

    for (int i = 0; i < letters.size(); i++) {  // 每次都是从0开始
        path.push_back(letters[i]);
        backtrack(digits, index + 1, path);  // 注意这里是index+1
        path.pop_back();
    }

适用场景：组合（可重复元素）

• 每个位置都需要从所有可能选项中重新选择

• 不同位置的选择是相互独立的（"abc"与"def"相互独立）

• 相当于 排列型回溯（但有一定约束）

2. i=start 开始的循环

    for (int i = start; i <= n; i++) {  // 从start开始，避免重复
        path.push_back(i);
        backtrack(n, k, i + 1, path);  // 注意这里是i+1
        path.pop_back();
    }

适用场景：组合（不可重复）

• 需要避免选择之前已经选过的元素

• 通过start参数控制选择范围

• 相当于 子集型回溯

特征	i=0 循环	i=start 循环
问题类型	电话号码字母组合 N皇后 全排列	组合总和 子集 组合
选择空间	每个位置有独立的候选集	从剩余元素中选择
去重方式	通过index跳到下一位置	通过start跳过已选元素
递归参数	backtrack(index + 1, ...)	backtrack(i + 1, ...)
是否可重复选择	同一元素可出现在不同位置	同一元素不可重复选择

例1：电话号码 "23"（i=0）

第一层（数字2）: 从 "abc" 中选 →先选a（ 可以选a, b, c）
第二层（数字3）: 从 "def" 中选 → 每个分支都重新从 "def" 开头选
结果: ["ad","ae","af","bd","be","bf","cd","ce","cf"]

例2：组合 C(4,2)（i=start）

第一层: 从 {1,2,3,4} 选2个数 → 先选1（可以选1，2，3，4）
选了1后，第二层: 从 {2,3,4} 选（避免重复选1）
结果: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]