
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 汉诺塔](#1. 汉诺塔)
[2. 占卜DIY](#2. 占卜DIY)
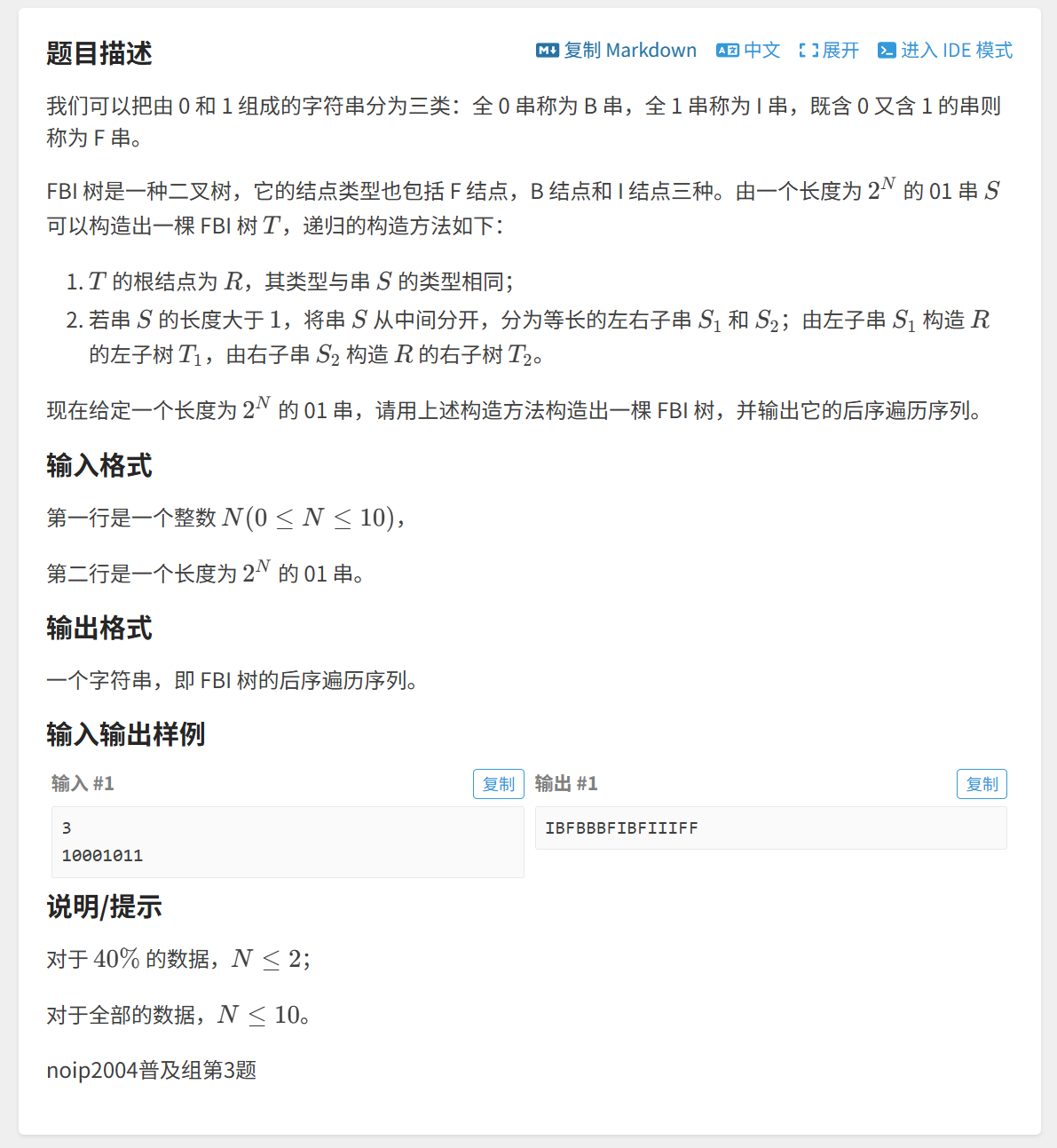
[3. FBI 树](#3. FBI 树)
前言
递归:函数自己调用自己。自己调用自己就说明执行的代码时一致的,这样的作用就是解决许多个重复子问题。因此利用递归解决问题的关键,便是是否有重复的子问题
递归初阶
1. 汉诺塔
题目链接:
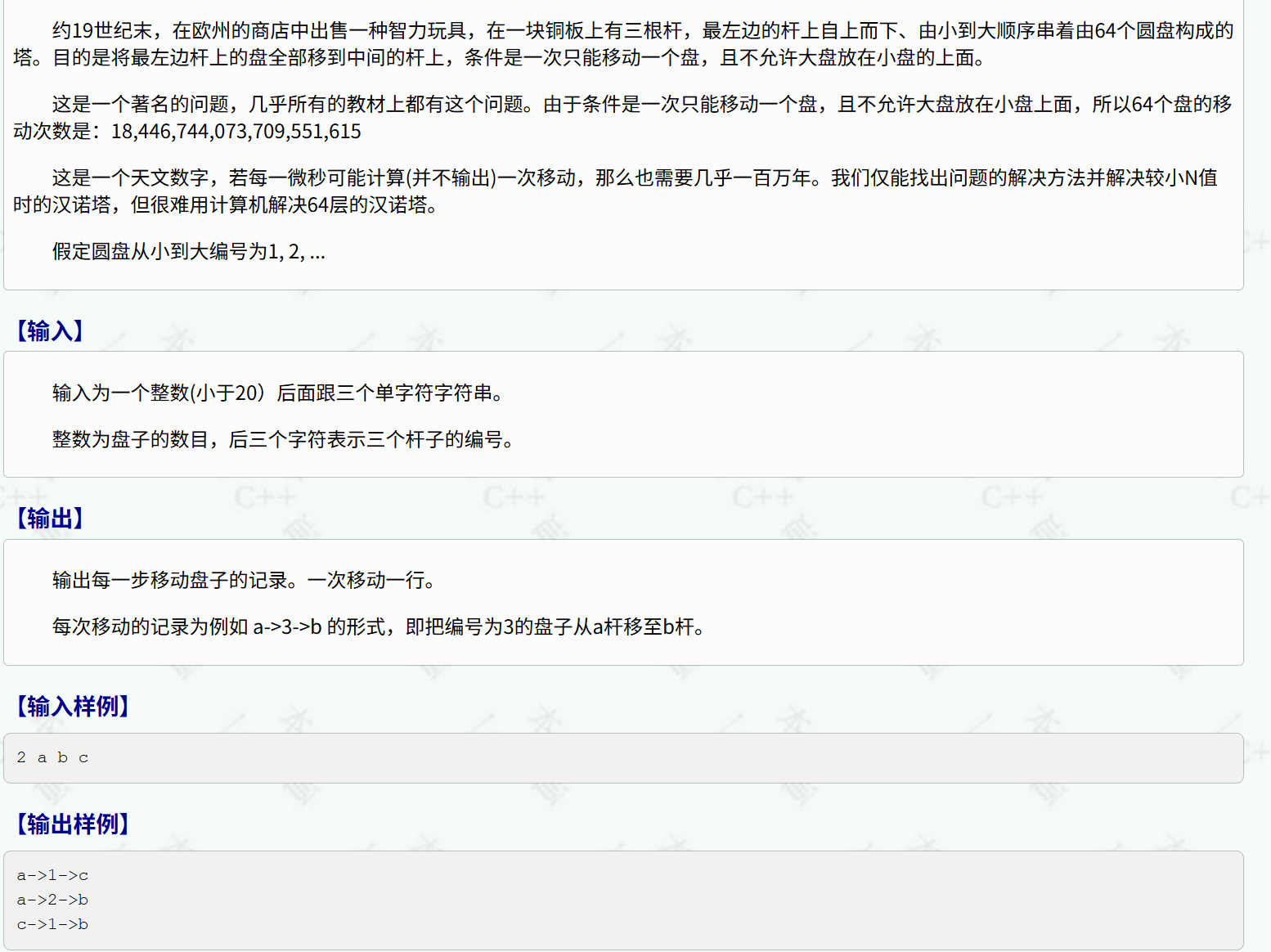
算法原理
这是一道很经典的递归问题,我们先从简单分析
假设n = 1,只有一个盘子,很简单,直接从a拿出来,放到b上即可
假设n = 2,那么我们就得借助b了,由于要遵循小盘子始终在大盘子上,那么可以这样做
- 1号盘子放在b上
- 2号盘子放在c上
- 1号盘子放在c上
如果n=3呢?我们这样看三个盘子
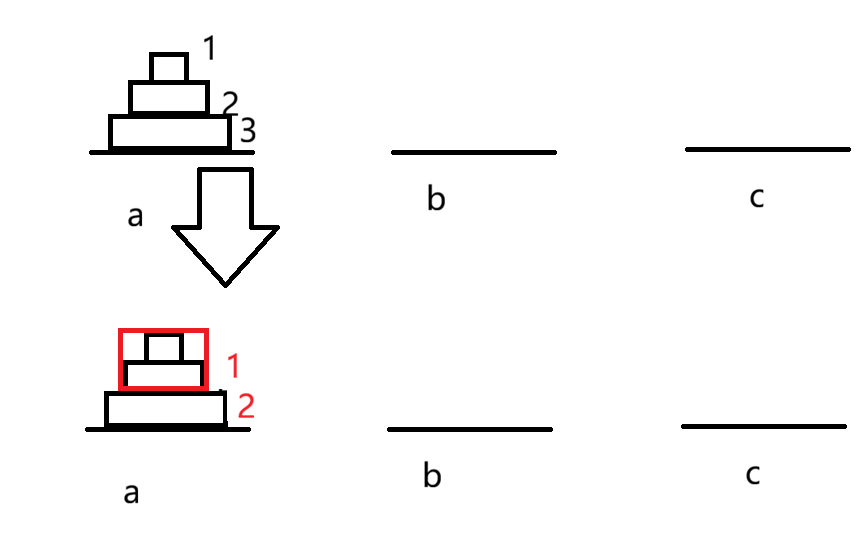
我们把3上面的2个盘子当作一个整体,那么我们就相当于是要把新的1和2移到c上,这个步骤和n = 2是一致的
其中我们要移动新的1时,就相当于是n = 2移动到c的情况,只不过移动的目标位置可能是a或者b,初始位置也不是a
以此类推到n > 3时,我们都可以把某个盘子上面的部分当作一个新的整体,那么无非就又回到了n = 2的情况;这样就变成了多个相同的子问题来解决
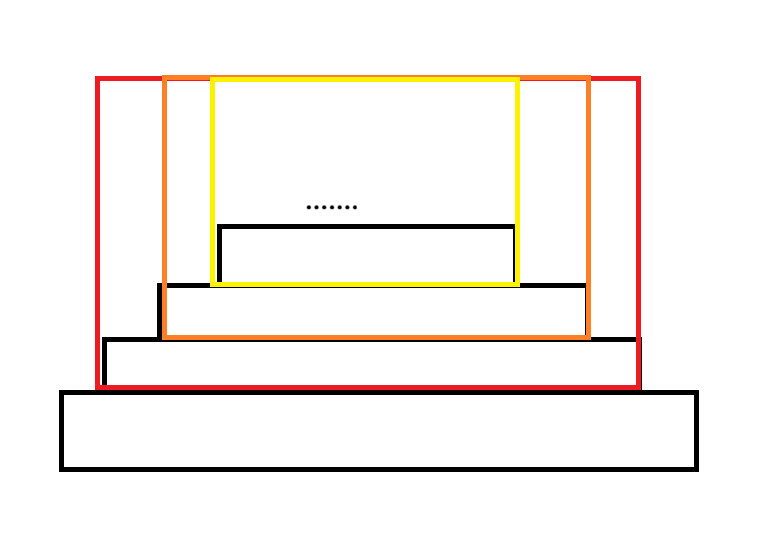
设计递归函数
重复子问题:将x个盘子,从begin柱子转移到end柱子上,其中通过tmp柱子作为中转;
具体操作:
- 先将beign上面x-1个盘子借助end转移到tmp上;
- 再把begin最下面一个盘子放在end上;
- 最后把tmp上面x-1个盘子借助begin转移到end上。
cpp
// 将 x 个盘⼦从 begin 移动到 end
// 其中 tmp 是中转站
void move(int x, char begin, char tmp, char end)实操代码
cpp
#include <iostream>
using namespace std;
int n;
char a, b, c;
// 将 x 个盘⼦从 begin 移动到 end
// 其中 tmp 是中转站
void move(int x, char begin, char tmp, char end)
{
if(x == 0) return;
move(x - 1, begin, end, tmp);
printf("%c->%d->%c\n", begin, x, end);
move(x - 1, tmp, begin, end);
}
int main()
{
cin >> n >> a >> b >> c;
move(n, a, c, b); // 把 a 上⾯ n 个盘⼦,借助 c 转移到 b 上
return 0;
}2. 占卜DIY
题目链接:
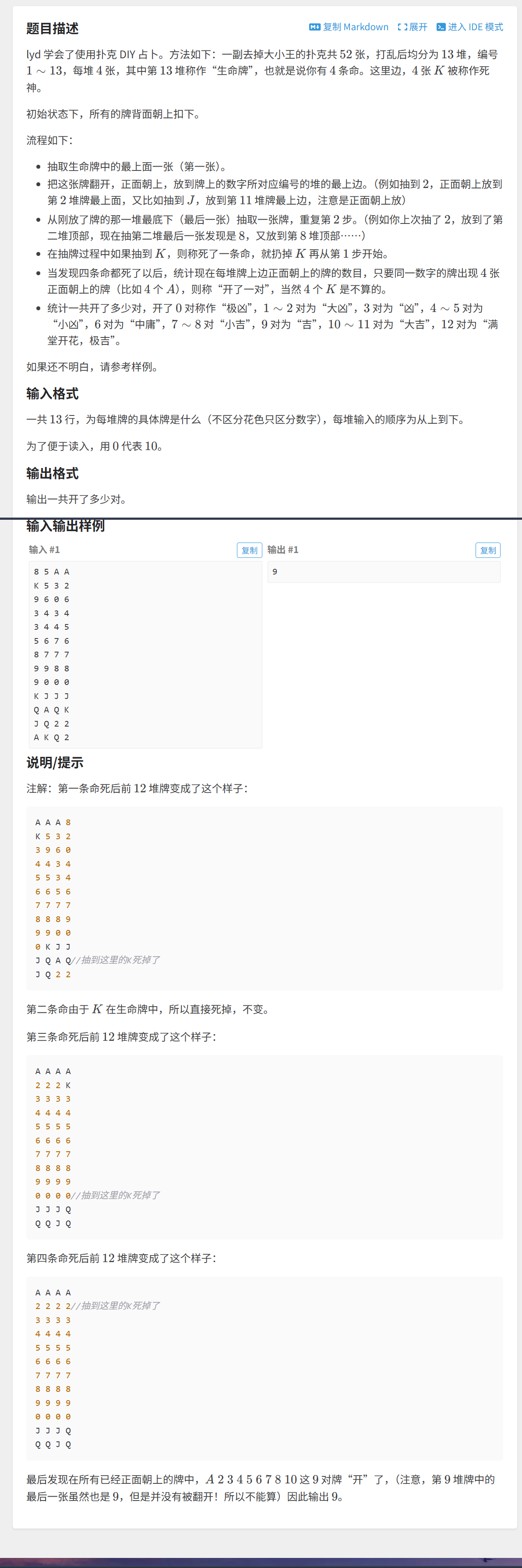
算法原理
整个模拟过程:
- 抽出第13堆最上面的牌c:
- 把第堆的最后一张拿出来;
- 拿到这张牌之后,重复2过程,直到拿到13
上述三步整个一循环,一直循环4次,直到把13堆上面的牌拿完。
重复子问题:
拿到一张牌x之后,把第x堆最后一张拿出来。
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
vector<vector<char>> v(14, vector<char>(4));
vector<int> arr(14, 0);
int getnum(char ch)
{
if (ch == '1')
return 13;
else if (ch >= '2' && ch <= '9')
return ch - '0';
else if (ch == '0')
return 10;
else if (ch == 'J')
return 11;
else if (ch == 'Q')
return 12;
else if (ch == 'A')
return 1;
else
return 0;
}
void func(char ch)
{
if (arr[0] == 4)
return;
int num;
num = getnum(ch);
arr[num]++;
char code;
if (num == 0)
code = '1';
else if (num == 13)
{
code = v[13][0];
v[13].erase(v[13].begin());
}
else
{
code = v[num][v[num].size() - 1];
v[num].erase(v[num].end()-1);
v[num].insert(v[num].begin(), ch);
}
func(code);
}
int main()
{
for (int i = 1; i <= 13; i++)
{
for (int j = 0; j < 4; j++)
{
char num; cin >> num;
v[i][j] = num;
}
}
func('1');
int ret = 0;
auto it = arr.begin() + 1;
while(it != arr.end()-1)
{
if (*it == 4)
ret++;
it++;
}
cout << ret;
return 0;
}3. FBI 树
题目链接:
算法原理
重复子问题:处理每一棵子树:
- 确定出该子树的类型;
- 然后从中间分开,先处理左子树,再处理右子树;
- 然后打印该子树的类型
如何快速判断出该子树的类型?因为我们要求的是一段区间内1的个数,我们可以利用「前缀和」数组求出这段区间和,然后在查询某段区间时,判断一下此时的区间和:
- 如果等于区间长度,说明是I类型;
- 如果等于0,说明是B类型;
- 否则就是F类型。
实操代码
cpp
#include <iostream>
#include <string>
#include <vector>
using namespace std;
struct node {
char val;
node* left;
node* right;
node(char _val) {
val = _val;
left = nullptr;
right = nullptr;
}
};
string s;
vector<int> v(1, 0);
char check(int left, int right) {
int ones = v[right] - v[left];
int length = right - left;
if (ones == length) return 'I';
if (ones == 0) return 'B';
return 'F';
}
node* create(int left, int right) {
if (right - left == 1) {
char ch = (s[left] == '1') ? 'I' : 'B';
return new node(ch);
}
int mid = (left + right) / 2;
node* newnode = new node(check(left, right));
newnode->left = create(left, mid);
newnode->right = create(mid, right);
return newnode;
}
void rearorder(node* root) {
if (root == nullptr) return;
rearorder(root->left);
rearorder(root->right);
cout << root->val;
}
int main() {
int num;
cin >> num;
cin >> s;
for (int i = 0; i < s.size(); i++) {
int num = s[i] - '0';
v.push_back(num + v[i]);
}
node* root = create(0, s.size());
rearorder(root);
return 0;
}