【算法基础篇】（四十九）数论之中国剩余定理终极指南：从孙子算经到算法竞赛

前言

在数论的璀璨星空中，中国剩余定理（CRT）无疑是一颗耀眼的明珠。它源于南北朝时期《孙子算经》中的 "物不知其数" 问题，历经千年沉淀，成为解决线性同余方程组的核心武器。在算法竞赛中，无论是模运算优化、大整数求解，还是组合计数问题，CRT 都能发挥关键作用。本文将从经典问题切入，层层拆解 CRT 的原理、构造思想与实现细节，结合洛谷经典例题，手把手教你掌握从理论到实战的全流程，让你在同余方程组问题中轻松破局。

一、问题溯源：从 "物不知其数" 到线性同余方程组

1.1 经典问题引入

《孙子算经》中有云："今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？" 翻译成数学语言，就是求解以下线性同余方程组：

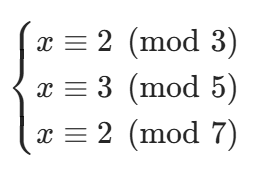
这个问题的最小正整数解是 23，而中国剩余定理正是为解决这类 "多模数同余" 问题而生。

1.2 线性同余方程组的定义

一般地，线性同余方程组的标准形式为：

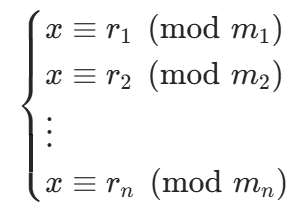
其中 m1,m2,...,mn 是模数，r1,r2,...,rn 是余数，我们的目标是找到满足所有方程的最小非负整数解 x。

1.3 CRT 的核心前提

中国剩余定理的适用条件是：所有模数 m1,m2,...,mn 两两互质。这一前提是 CRT 构造解的基础，后续我们会看到，正是因为模数互质，才能保证逆元存在，从而顺利构造出满足所有方程的解。

二、CRT 的原理：构造法的精妙之处

CRT 的核心思想是 "分而治之、逐步构造"------ 先为每个方程构造一个局部解，使得该解仅满足当前方程，而对其他方程的余数为 0；再将所有局部解相加，得到满足所有方程的全局解。

2.1 构造步骤拆解

设方程组有 n 个方程，模数两两互质，定义：

则方程组的一个解为：

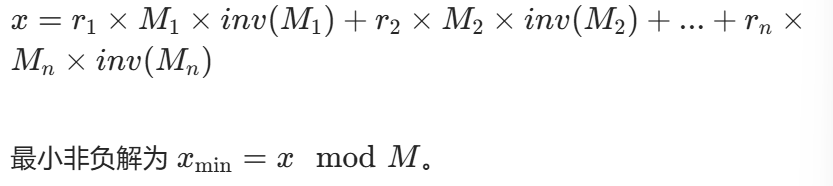
2.2 构造逻辑验证

为什么这样的构造能满足所有方程？以第 i 个方程为例：

对于 j≠i，Mj 包含 mi 这个因子（因为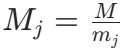，而 mi 是 M 的因子且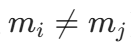），因此；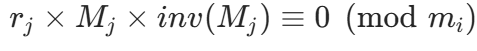
对于 j=i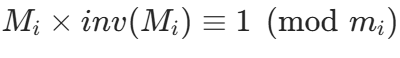，，因此；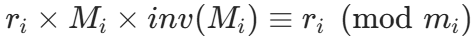
叠加后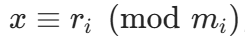，，恰好满足第 i 个方程。

三、核心工具：逆元与快速乘的实现

要实现 CRT，必须解决两个关键问题：乘法逆元求解 和大整数溢出防护。

3.1 乘法逆元求解（扩展欧几里得算法）

由于 CRT 中模数两两互质，Mi 与 mi 互质，逆元一定存在。我们用扩展欧几里得算法求解逆元，该方法适用于任意互质的模数对，通用性强。

扩展欧几里得算法原理

扩展欧几里得算法不仅能计算 a 和 b 的最大公约数，还能找到整数 x 和 y，使得 ax+by=gcd(a,b)。当 a 与 b 互质时，gcd(a,b)=1，此时 x 就是 a 模 b 的逆元。

C++ 实现扩展欧几里得算法

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;

// 扩展欧几里得算法：返回gcd(a,b)，通过引用返回ax + by = gcd(a,b)的特解x,y
LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

// 求a模m的逆元（a与m互质）
LL get_inv(LL a, LL m) {
    LL x, y;
    exgcd(a, m, x, y);
    // 转为最小正整数逆元
    return (x % m + m) % m;
}

int main() {
    LL a = 35, m = 3;
    cout << a << "模" << m << "的逆元为：" << get_inv(a, m) << endl; // 输出2
    return 0;
}

3.2 快速乘：大整数溢出防护

当模数较大时（如 1e5×1e5×1e5=1e15），直接乘法会超出 long long 范围导致溢出。快速乘（又称龟速乘）通过将乘法转化为加法，结合模运算，避免溢出。

快速乘原理

快速乘的核心是二进制分解：将 a×b 分解为 a×20+a×21+...+a×2k，每次累加后取模，确保中间结果不溢出。

C++ 实现快速乘

cpp 复制代码

// 快速乘：计算(a*b) mod p，避免溢出
LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) {
            ret = (ret + a) % p;
        }
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    LL a = 1e18, b = 1e18, p = 1e9 + 7;
    cout << qmul(a % p, b % p, p) << endl; // 输出(a*b) mod p的结果
    return 0;
}

四、CRT 的完整 C++ 实现

结合逆元求解和快速乘，我们可以写出 CRT 的通用实现，适用于所有模数两两互质的线性同余方程组。

4.1 实现代码

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 15; // 方程组最大方程数

LL r[N], m[N]; // r[i]为余数，m[i]为模数
int n; // 方程个数

// 扩展欧几里得算法
LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

// 快速乘
LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

// 中国剩余定理：返回最小非负解，无解返回-1（模数互质时一定有解）
LL crt() {
    LL M = 1;
    for (int i = 0; i < n; ++i) {
        M *= m[i]; // 全局模数
    }
    LL ret = 0;
    for (int i = 0; i < n; ++i) {
        LL Mi = M / m[i];
        LL inv_Mi = 0;
        // 求Mi模m[i]的逆元
        exgcd(Mi, m[i], inv_Mi, ignore);
        inv_Mi = (inv_Mi % m[i] + m[i]) % m[i];
        // 累加局部解：r[i] * Mi * inv_Mi，用快速乘避免溢出
        ret = (ret + qmul(qmul(r[i], Mi, M), inv_Mi, M)) % M;
    }
    // 确保返回最小非负解
    return (ret % M + M) % M;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    // 输入方程个数
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> m[i] >> r[i];
    }
    LL ans = crt();
    cout << "最小非负解：" << ans << endl;
    return 0;
}

4.2 代码分析

时间复杂度 ：O(nlogm)，其中 n 是方程个数，logm 是扩展欧几里得算法和快速乘的时间复杂度；

空间复杂度 ：O(n)，仅需存储模数和余数数组；

适用性：适用于所有模数两两互质的线性同余方程组，返回最小非负解；

溢出防护 ：通过快速乘 qmul 确保大整数乘法不溢出，支持模数乘积达 1e18 级别。

五、实战例题 1：洛谷 P1495 【模板】中国剩余定理 / 曹冲养猪

题目链接：https://www.luogu.com.cn/problem/P1495

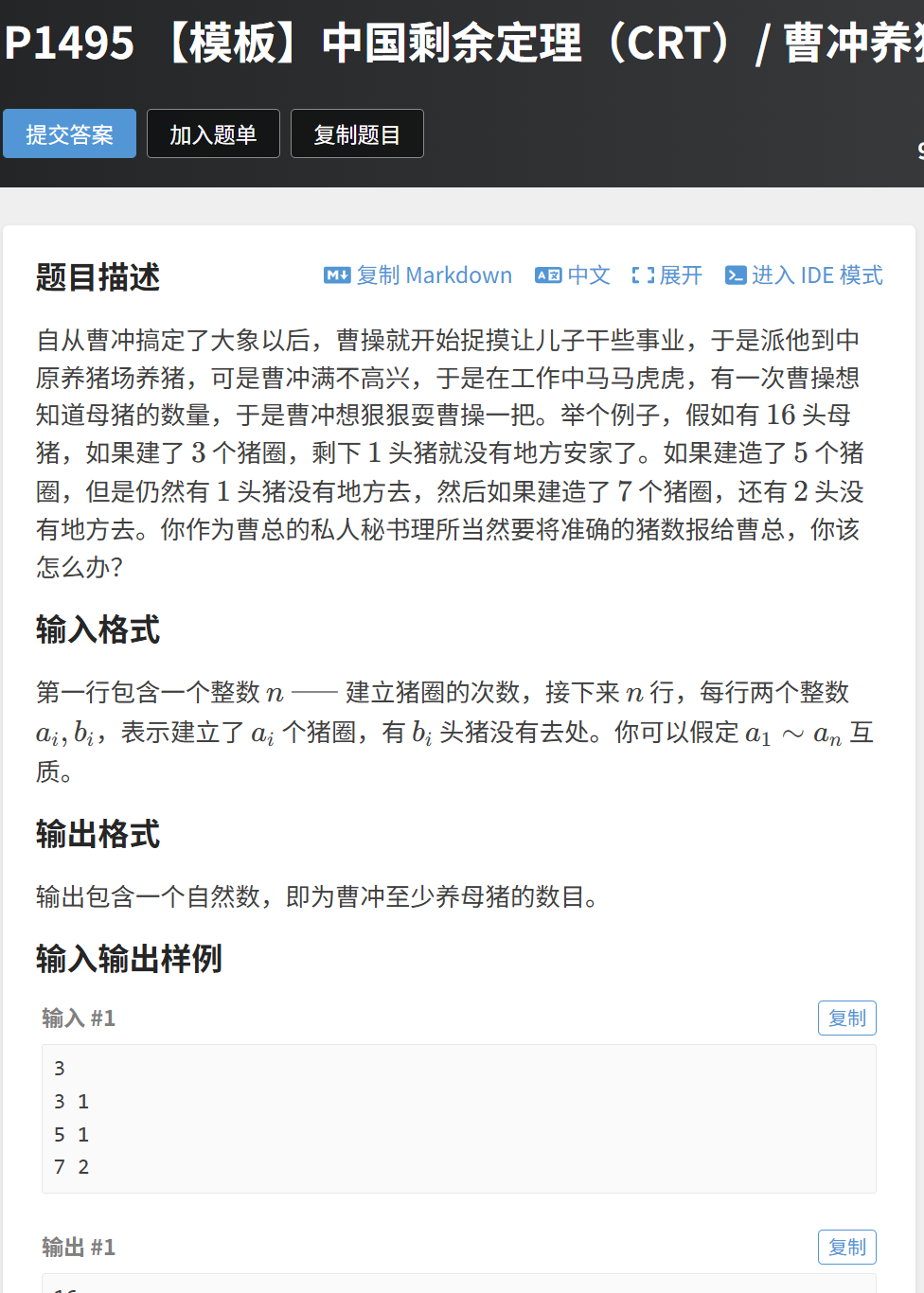
5.1 题目分析

题目描述：曹冲养猪，建 ai 个猪圈剩 bi 头猪（ai 两两互质），求最少养猪数量。

输入描述：第一行 n，接下来 n 行每行两个整数 ai、bi（ai 为模数，bi 为余数）。

输出描述：最小正整数解。

示例输入：33 15 17 2

示例输出：16。

5.2 解题思路

直接套用 CRT 模板，将 ai 作为模数 mi，bi 作为余数 ri，调用 CRT 函数即可。

5.3 C++ 实现

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 15;

LL r[N], m[N];
int n;

LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

LL crt() {
    LL M = 1;
    for (int i = 0; i < n; ++i) M *= m[i];
    LL ret = 0;
    for (int i = 0; i < n; ++i) {
        LL Mi = M / m[i];
        LL inv_Mi, y;
        exgcd(Mi, m[i], inv_Mi, y);
        inv_Mi = (inv_Mi % m[i] + m[i]) % m[i];
        ret = (ret + qmul(qmul(r[i], Mi, M), inv_Mi, M)) % M;
    }
    return (ret + M) % M;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> m[i] >> r[i];
    }
    cout << crt() << endl;
    return 0;
}

5.4 代码验证

示例输入中，模数 m=[3,5,7]，余数 r=[1,1,2]：

全局模数 M=105；

局部解分别为：1×35×2=70，1×21×1=21，2×15×1=30；

总和 70+21+30=121，121 mod 105=16，与示例输出一致。

六、实战例题 2：洛谷 P3868 [TJOI2009] 猜数字

题目链接：https://www.luogu.com.cn/problem/P3868

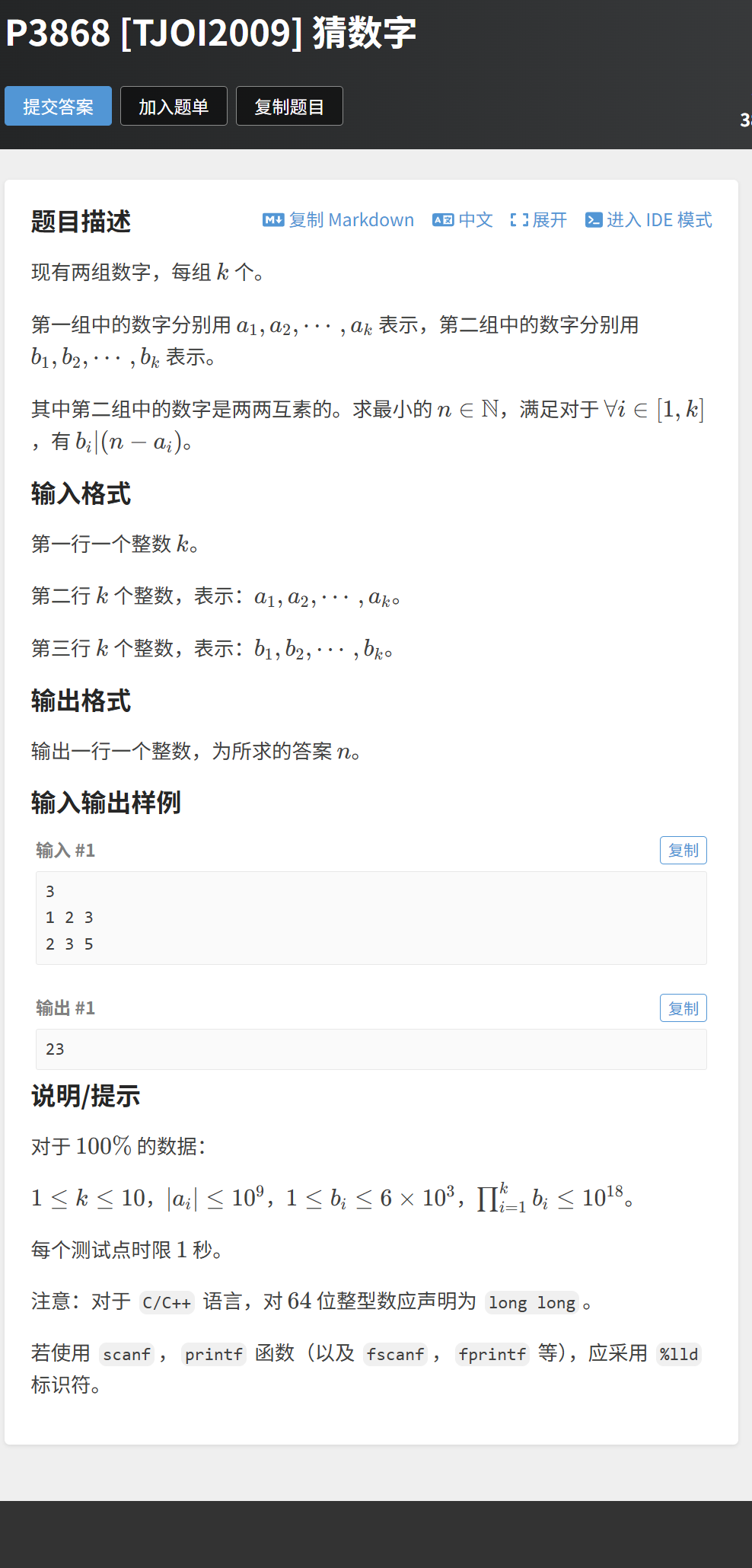
6.1 题目分析

题目描述：给定两组数字 a1...ak 和 b1...bk（bi 两两互质），求最小的 n 使得 bi∣(n−ai)（即 n≡ai(modbi)）。

输入描述：第一行 k，第二行 a1...ak，第三行 b1...bk。

输出描述：最小正整数 n。

示例输入：31 2 32 3 5

示例输出：23。

6.2 解题思路

方程转化：n≡ai(mod bi)，直接对应 CRT 的标准形式；

注意点：ai 可能为负数，需先将余数调整为非负（ri=(aimodbi+bi)modbi）。

6.3 C++ 实现

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 15;

LL r[N], m[N];
int n;

LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

LL crt() {
    LL M = 1;
    for (int i = 0; i < n; ++i) M *= m[i];
    LL ret = 0;
    for (int i = 0; i < n; ++i) {
        LL Mi = M / m[i];
        LL inv_Mi, y;
        exgcd(Mi, m[i], inv_Mi, y);
        inv_Mi = (inv_Mi % m[i] + m[i]) % m[i];
        // 累加时确保余数非负
        ret = (ret + qmul(qmul((r[i] % m[i] + m[i]) % m[i], Mi, M), inv_Mi, M)) % M;
    }
    return (ret + M) % M;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> r[i];
    }
    for (int i = 0; i < n; ++i) {
        cin >> m[i];
    }
    cout << crt() << endl;
    return 0;
}

七、常见误区与避坑指南

7.1 模数不互质直接套用 CRT

误区：忽略 CRT "模数两两互质" 的前提，直接代入代码导致错误；

避坑：先检查所有模数对的最大公约数，若存在非 1 的情况，改用 EXCRT；

验证方法：对于模数 m1,m2,...,mn，需满足 gcd(mi,mj)=1（i=j）。

7.2 大整数乘法溢出

误区：直接使用 a * b % p 计算，当 a 和 b 均为 1e9 时溢出；

避坑：统一使用快速乘 qmul 替代直接乘法，确保中间结果不溢出。

7.3 余数为负数未调整

误区：当 ri 为负数时（如 x≡−1(mod5)），直接代入计算；

避坑：将余数调整为非负：。

7.4 逆元求解错误

误区：使用费马小定理求逆元但未确认模数为质数；

避坑：CRT 中模数不一定是质数，优先用扩展欧几里得算法求逆元（通用无限制）。

7.5 全局模数计算溢出

误区：当 n 较大（如 n=10，每个模数 1e5），M=1e510 远超 long long 范围；

避坑：此时需用 __int128 存储 M，或在快速乘中实时取模，避免全局模数溢出。

总结

中国剩余定理是解决线性同余方程组的经典算法，其核心是 "构造法"，通过局部解叠加得到全局解。如果在学习过程中遇到具体题目无法解决，或想了解 EXCRT 的详细实现，可以随时留言交流。后续将持续更新数论进阶内容，敬请关注！

【算法基础篇】（四十九）数论之中国剩余定理终极指南：从孙子算经到算法竞赛

目录

前言

一、问题溯源：从 "物不知其数" 到线性同余方程组

1.1 经典问题引入

1.2 线性同余方程组的定义

1.3 CRT 的核心前提

二、CRT 的原理：构造法的精妙之处

2.1 构造步骤拆解

2.2 构造逻辑验证

三、核心工具：逆元与快速乘的实现

3.1 乘法逆元求解（扩展欧几里得算法）

扩展欧几里得算法原理

C++ 实现扩展欧几里得算法

3.2 快速乘：大整数溢出防护

快速乘原理

C++ 实现快速乘

四、CRT 的完整 C++ 实现

4.1 实现代码

4.2 代码分析

五、实战例题 1：洛谷 P1495 【模板】中国剩余定理 / 曹冲养猪

5.1 题目分析

5.2 解题思路

5.3 C++ 实现

5.4 代码验证

六、实战例题 2：洛谷 P3868 [TJOI2009] 猜数字

6.1 题目分析

6.2 解题思路

6.3 C++ 实现

七、常见误区与避坑指南

7.1 模数不互质直接套用 CRT

7.2 大整数乘法溢出

7.3 余数为负数未调整

7.4 逆元求解错误

7.5 全局模数计算溢出

总结