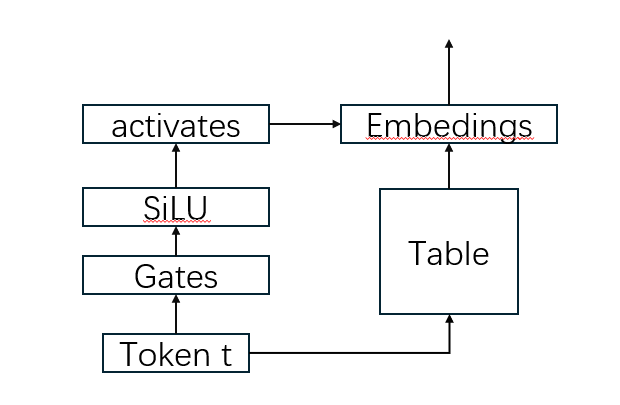
本文介绍一篇与DeepSeek颇有渊源的一片工作,来自meta; 同样使用了embedding table 来存储词向量,在FFN层作为改进,进行memory 注入;
这里的新一代架构是指Memory-Augmented Transformer, 顾名思义,为现有的Transformer注入记忆机制.记忆是DeepSeek那篇Nagram 主要sale的点,STEM并没有明确提这个概念,但是不约而同地采用了Learnable embeddings为 transformer注入知识;
本文将试图回答几个问题:
1.MAT 架构优势体现在哪些方面?
2.为什么一定要在FFN 这个层面进行注入?
3.MAT 迁移到vision 有多大可能?
Intro
1.稀疏计算是有效利用模型参数的一个方法,因为这能享受模型参数增多带来的好处,同时又不会成比例地增加每个token的计算(相比较于dense model 需要将每个token 完整过一遍模型);
2.但是MoE 还是会被non-uniform问题所困扰,因为训练的时候不均衡,导致无效参数,并且推理的时候也会不均衡;并且不好训练,需要精心调参 load-balancing objectives ;
3.另外,从系统角度,一味增加experts数目的话,会导致带宽利用率下降,并且放大通讯开销;如果细粒度的专家子网络过小的话,又会导致kernel 利用率下降(这里没看懂);
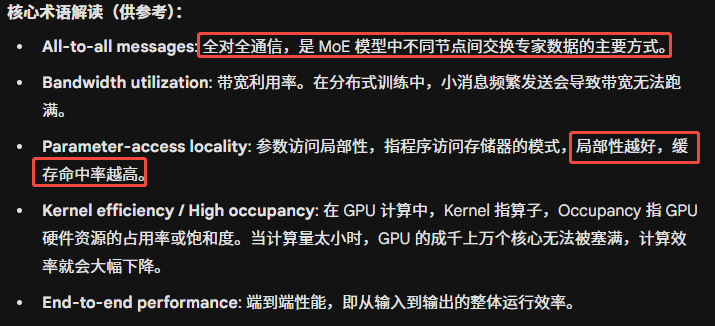
4.这里给出了需求:
要能稳定优化;
Expert 利用率要高,每个expert 都要学到有用的representation;
减少通讯开销;
最好还有一定的可解释性;
5.本文提出token-indexed static sparsity,没有routing时延,支持cpu offloading, 因此node之间不需要做通讯;优点如下:
更稳定的训练;
更强的知识表征能力,信息存储能力更好;
更强的long-context 能力;
更高效:省参数,省FLOPS; 因此对于计算密集的prefill以及内存密集的decoding都很友好;
Background
1.MoE相当于将FFN 变成n 个 FFN,然后各自的输出再由一个router 的score进行筛选,只选择top-k experts 组成一个small set;
2.Hash-layer MoE: 由于训练经常不平衡,难以优化,hash-layer MoE实现了基于token id的静态映射;

t是当前token的id,词表中的索引,而不再是Token的隐藏层表示;
预先定义一个hash函数 hash(t)
固定路径:对于每一个特定的单词,在模型的所有层中,或者特定的hash层中始终被路由到相同的专家组;
Token id 是均匀分布的,因此好的哈希函数本身就能保证每个专家负责的词量大致相等;
3.scaling the number of Experts: 后续有工作将expert 数目推向上万级别,但是出现了两个问题:
即使使用了hash-layer 映射,但是有些常用词本身出现频率特别高,而有些词出现频率比较低,这样进一步导致了负载不均衡 ;
另一个问题是通信开销变大 ,通信过程产生大量的细碎负荷,降低了通讯效率;
4.Per Layer embedding
部分共享参数:PLE 在不同的专家网络间共享FFN块的门控投影,gate projection, 以及下采样映射,down projection;
PLE 并没有替代FFN,而是在每个decoding layer 增加一个PLE block,因此每一层的输出是FFN的输出+PLE的输出;
可以按需提取,CPU存储,可以通过查表实现。可以遇到生词,或者固定搭配的时候查一下词表,而不需要整个背下来(优化到参数中);
STEM
https://ai.google.dev/gemma/docs/gemma-3n?hl=zh-cn
STEM的FFN 完全由激活查表中的词向量代替;(这也是和PLE的区别,PLE中一半FFN一般embedding,两个相加)
Insight
1.首先是从kv memory的角度来看, FFN 两层线性,上采样和下采样,以及中间的非线性激活,可以视为是一种内容检索/寻址(content-addressable k-v memory);
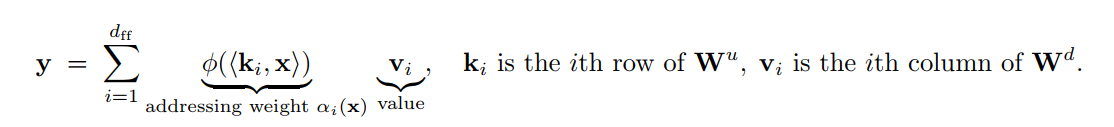
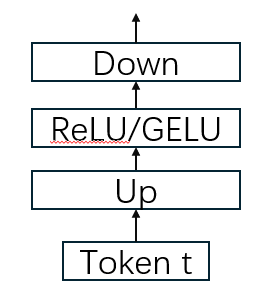
在这里,Wu可以视为key, 而Wd可以视为value, 非线性决定寻址的稀疏性/选择性;如ReLU可以作为硬门控,GELU可以作为软门控;
而Gated Linear Units可以丰富这种memory,将寻址分为内容寻址和gate 寻址;
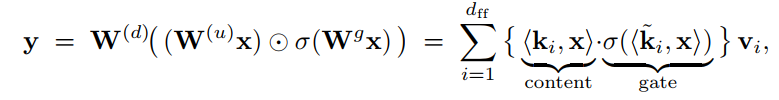
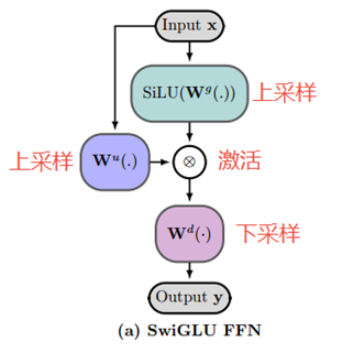
相当于对记忆槽(memory slots)进行了放大或抑制, 引入第二组key, 依赖于查询的(input-conditional),对记忆槽逐槽放大或者抑制;这里的非线性单元是SiLU; 起到一个双重校验的作用,Wu做内容寻址,决定取出哪些memory,gates起到决定取出的memory 是否重要的作用;
正是这种查询'memory'的理解 催生了STEM;
Design Choice
尝试用STEM embedding table去替代up projection 以及gate projection;
Down projection不能被替代,因为会Break the forward path;

结论是替换up-projection会提升的多,而替换gates则提升的少;
Better Information Storage capability
根据记忆视角,上投影负责为特征查找生成"地址",而门控投影则提供依赖于上下文的调制以实现更有效的检索。如果将门控投影替换为"与上下文无关(Context-agnostic)"的固定嵌入表,会削弱模型的能力。因此,STEM 最终选择只用层级嵌入表替换上投影。
传统模型必须通过上投影矩阵 W u \mathbf{W}^u Wu 实时计算出地址。由于需要在相对较低的维度 d f f n d_{ffn} dffn里挤进海量的概念,模型被迫使用叠加态(Superposition)机制。这意味着不同概念的地址向量之间会存在较高的相关性(纠缠),导致提取知识时不够精准。
Knowledge Specificity & Interpretability
由于这些embedding和tokens是绑定在一起的,因此可以充当steering vectors的作用;
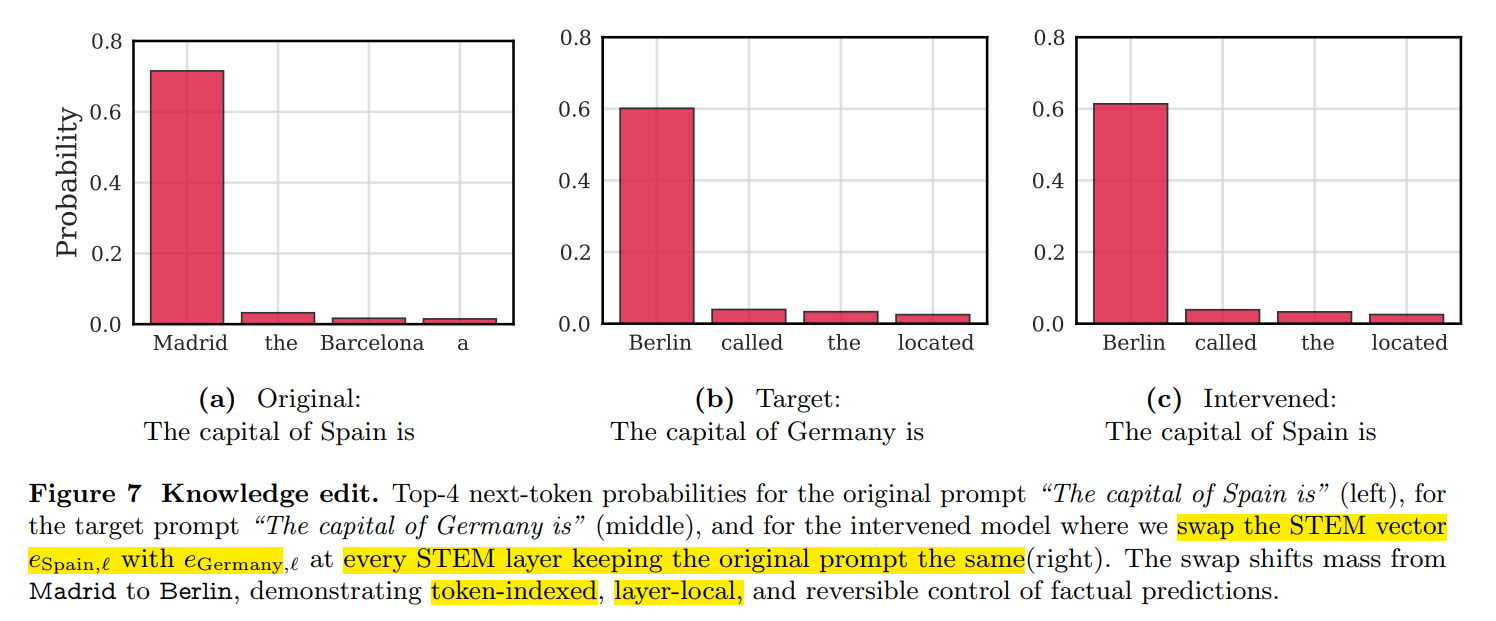
通过修改每一个STEM层中具体token,可以控制输出;输入都是一样的'The captital Spain is ';
Efficiency
就单层而言,对于computation 以及 memory 都是极其友好的;
Computation: training and prefill
Memory: decoding
理论分析: 首先忽略逐元素的操作和偏置项;因为逐元素的操作是o(n) 对于训练,backward是forward约两倍计算(主要是矩阵乘);
Training
B x L x d, d f f d_{ff} dff为FFN 的维度;
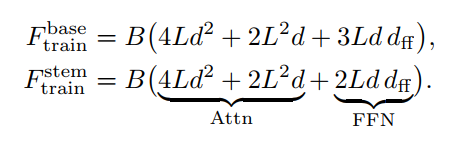
python
# 先忽略batch 维度
q = linear_q(x)
k = linear_k(x)
v = linear_v(x)
以上三次为L*d*d,因为输入x是l*d, 权重是d*d,输出是l*d, 对于输出的每一个元素,需要计算d次乘法,(d-1)次加法.这里暂且忽略加法,则l*d个元素,需要执行l*d*d次乘法;
reshape之后:
outputs = softmax(q@k'/sqrt(d)) @ v
MultiHeadAttn(QKV) = cat(outputs1, outputs2,...,outputsn) @ linear_o
多头一次o投影, 仍然是l*d过d*d权重得到l*d,因此计算复杂度也是l*d*d;
因此投影操作总计4Ld**2
Attention 部分有2L**2*d
score = f(Q @ K') 的时候,l*d, d*l, 输出是l*l, 每个元素是d次乘法,(d-1)次加法,忽略加法后是 L*L*d
score @ V的时候, 输入是l*l,l*d,输出是l*d, 每个元素是l次乘法,(l-1)次加法,忽略加法后是L*L*d
因此4次映射加上score 计算和score 激活总共是 4Ld**2+2dL**2
python
FFN-baseline
up:
hiddens_up = linear_up(x)
gates:
hiddens_gate = linear_gate(x)
x' = hiddens_up * hiddens_gate # 逐元素乘法,忽略
down:
hiddens_down = linear_down(x')
up&gates:
一次linear 操作,输入ld,up权重d x dff, down权重 dff x d, gate权重 d x dff
输出是l x dff, 每个元素需要d次乘法,(d-1)次加法;忽略加法,则复杂度为2 * l * dff * d
down:
输入是l x dff, 权重是dff x d
输出是l x d, 每个元素执行dff次乘法,... 则复杂度为l x d x dff
所以FFN-baseline 计算复杂度为3 x l x d x dff
STEM:
不需要up这个操作,直接查表获取,因此复杂度为2 x l x d x dff
Inference:
推理阶段的prefill是compute-bound,而decoding 是memory-bound
python
主要瓶颈在于memory访存
复杂度来源于三部分,attention 参数,FFN 参数,KV cache;
# attn:
Linear_QKVO
4 * d * d
# KV Cache
2 * L * d
# FFN
linear_up_down_gates
3 * d * dff
total = 4d**2 + 2LD + 3d*dff
而STEM 中少了up-projection的参数的访存,因此少了ddff;

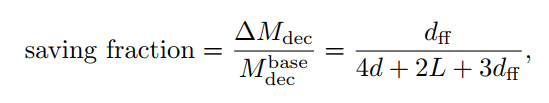
因此推理和训练省掉的计算量或者访存量公式是一样的;
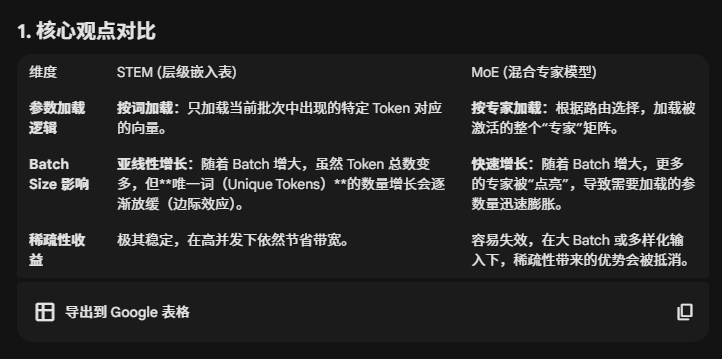
齐夫定律: 随着 Batch Size 变大,会遇到重复的词。由于自然语言的幂律分布,Batch 越大,新增的唯一词就越少。
但是batch 足够大,对于MoE模型而言,几乎所有的专家都会被激活。此时,你必须加载所有专家的参数,原本 MoE 节省带宽的"稀疏性"优势就彻底消失了,退化成了密集模型。
VRAM and communication savings
MoE 需要频繁访存FFN子网络参数,但是STEM可以将embedding table offload到cup内存中,由于是token-indexed,可以直接查表获得,并不需要额外的计算;
prefetch: 可以将使用频率高的 embedding 预先加载,不需要卸载到cpu;这样也可以加速;
长文本下细粒度稀疏性
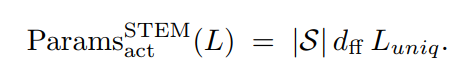
由于每层每个token只分配唯一的embedding, 所以随着序列长度L增加,看起来激活参数在随着L线性增加,但其实由于齐夫定律,这种增加是亚线性的;

论文指出,这种方法仅仅是改进了门控前馈网络, Gated FFN;因此和MoE结合是可以实现的;
另外 FFN 的输入x已经做了上下文的交互(attn),因此这时候的gates 具备上下文能力;

索引阶段只做信息的检索,决策权留给后面的gate;
Knowledge Editing with. STEM
这里控制模型原始输入,通过修改STEM 中索引出的embedding 来控制最终的输出;
Source > target: 采取padding。或者 repeat
Source < target: 则取最相近语意的embedding,去掉function word or less informative subwords;

还有最终的一个方案是计算 targets 的平均值,这个效果也很好;
System Implementation
1.推理的时候将STEM embedding tables offload 到CPU上,因为是可以查表获取,因此可以算到某层的时候再prefetch;
2.prefetch 更容易,因为token ids是已知的;另外为了进一步加速,按照Zipfian distribution 为高频词进行LFU cache;即在SRAM/L2 cache中开辟一小块空间,专门存放最常用的token 向量;能保证80%以上的命中率;
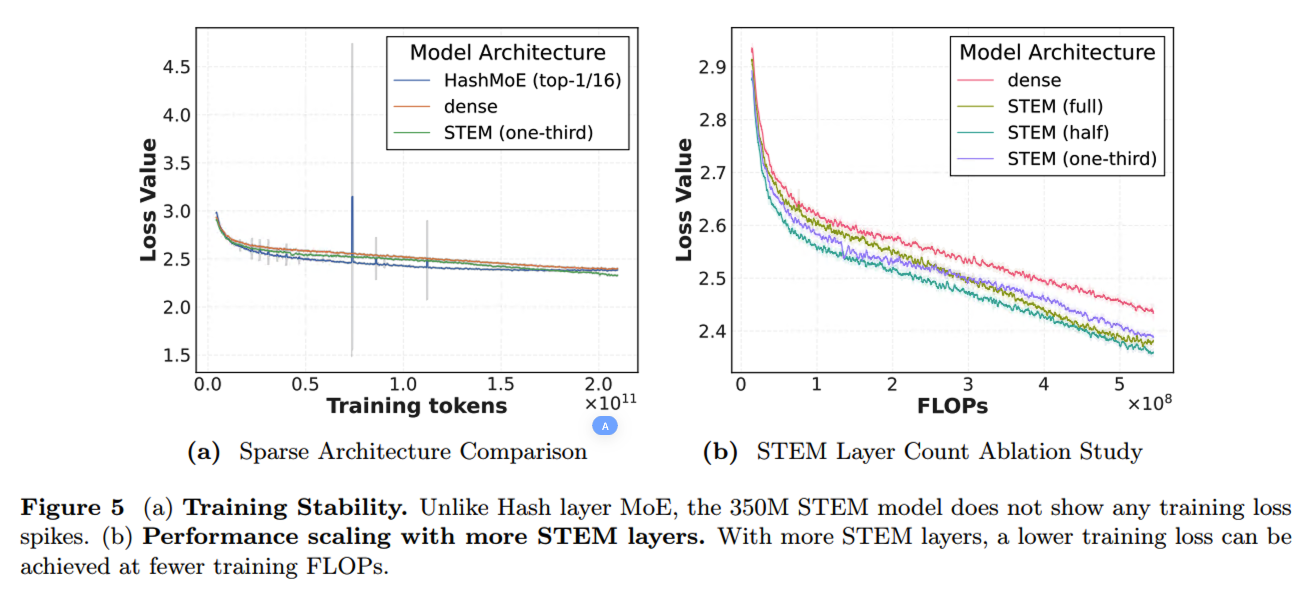
实验部分就省略了
写在最后
最后尝试回答开篇的几个问题:
1.MAT 架构优势体现在哪些方面?
第一点就是同样总的learnable参数条件下,更省显存,更省计算; 这样能够在有限的计算资源下进一步scale 模型的规模,以享受参数增多带来的更强的建模能力;
第二点是可解释性更好,每一个token id对应的embedding 具有实际的意义,替换后可以控制输出;
2.为什么一定要在FFN 这个层面进行注入?
因为在一个block中,attention 用于上下文的交互,只有看过上下文的状态再进行门控才更有意义,这样能让gate根据上下文来放大或者抑制不同的embedding具体的含义;
3.MAT 迁移到vision 有多大可能?
这里有一个最大的问题,就是token id 进行索引,因为语言是离散表征,天然可以有token id,但是视觉是没有这个概念的;如果采用离散的视觉表征,那么确实可以无缝嫁接,但是否能起到一样的效果,确实需要进一步的验证;