C++ 队列 宽度优先搜索 BFS 力扣 662. 二叉树最大宽度 每日一题

文章目录

• 一、题目描述
• 二、为什么这道题值得你花几分钟弄懂？
• 三、题目解析
• 四、算法原理
• • 暴力（❌不可取）
  • 利用数组来二叉树，给节点编号
  • 细节注意
• 五、代码实现
• • 模拟过程
  • 复杂度分析
• 六、下题预告

一、题目描述

题目链接：力扣 662. 二叉树最大宽度

题目描述：

示例 1：

输入：root = [1,3,2,5,3,null,9]

输出：4

解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。
示例 2：
输入：root = [1,3,2,5,null,null,9,6,null,7]

输出：7

解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。
示例 3：

输入：root = [1,3,2,5]

输出：2
提示：

树中节点的数目范围是 [1, 3000]

-100 <= Node.val <= 100

二、为什么这道题值得你花几分钟弄懂？

这道题是二叉树层序遍历（BFS）的经典变形题，也是面试中考察"二叉树遍历+细节处理"的高频题。它既考验我们对二叉树层序遍历的基础掌握，又考察我们对"索引标记""数值溢出"等细节的把控能力，是夯实二叉树BFS应用的必做题。

题目核心价值

• BFS遍历的"进阶试炼"：基础的层序遍历只需要按层访问节点，而这道题需要在遍历的同时记录节点的位置信息，是对BFS核心逻辑的深化应用。
• 满二叉树索引思想的落地：将二叉树节点映射为满二叉树的索引，把"宽度计算"转化为"索引差值计算"，这种数学映射思维是解决树结构问题的常用技巧。
• 边界与溢出的考量：直接使用普通整数会面临溢出风险，这道题能训练我们对数据类型选择（如unsigned int）和边界场景的敏感度。
• 面试的"区分度题目"：基础解法容易想到，但能考虑到溢出、空节点处理等细节的解法，才能体现你的编码严谨性，是面试中区分普通选手和优秀选手的关键。
• 代码简洁性的体现：最优解法逻辑清晰且代码短小，能考察我们"用最少代码实现核心逻辑"的能力，契合面试中"代码简洁性"的评分标准。

面试考察的核心方向

1. 层序遍历的理解深度：能否灵活运用BFS实现按层处理二叉树节点，而非单纯背诵模板。
2. 索引标记的思维能力：能否想到用满二叉树的索引规则标记节点位置，将"宽度计算"转化为数学问题。
3. 代码的健壮性：是否考虑到索引溢出问题，能否选择合适的数据类型避免计算错误。
4. 复杂度分析的准确性：能否快速分析出时间/空间复杂度，理解层序遍历的时间代价和辅助空间的使用逻辑。

三、题目解析

我最开始在做这道题乍一看以为是简单的用层序遍历来找哪一层的节点数最多是多少，但是后来被没有好好读题狠狠的教育了一下/(ㄒoㄒ)/~~，这道题让我们找的最大宽度是包含中间的空节点的。

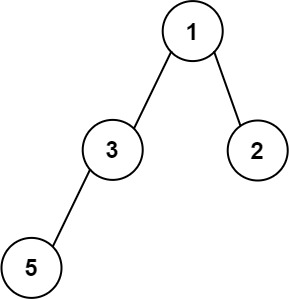
比如这棵树：

如果只统计每层非空节点的数量，各层数量分别是 1、2、2，最大值是 2；但题目要求的 "宽度"需要把中间的空节点都算上，第 3 层的宽度是 4（4 和 5 之间有 2 个空节点，加上自身共 4 个位置），这才是最终答案。

道题很容易因为粗心踩了**把"节点数量"等同于"宽度"**的坑。节点数量只统计非空节点，而宽度是"层内最左和最右非空节点之间的所有位置数"------哪怕中间全是空节点，也要计入宽度。

四、算法原理

暴力（❌不可取）

看到这道题时，我的第一反应是沿用层序遍历的常规思路：把每一层的所有节点（包括空节点） 都加入队列，再遍历该层节点找到最左和最右的非空节点，通过两者的位置差计算宽度。但实际尝试后发现，这种思路存在两个致命问题：

问题1：空节点的边界难以界定

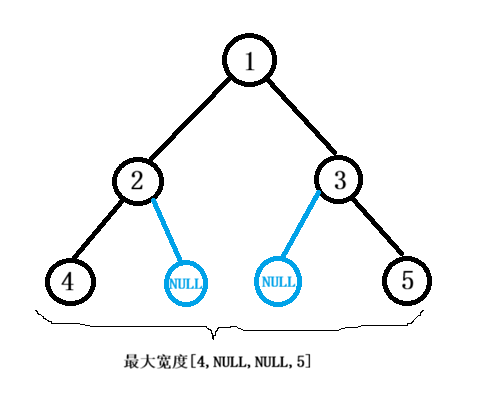
暴力法的核心漏洞是无法区分"有效区间内的空节点"和"边缘的空节点"。比如下图的场景：

按暴力法的逻辑，第4层会把8个节点（包含空节点）全部加入队列，队列长度为8，但该层实际有效宽度是7，因为最右侧的空节点属于"边缘空节点"，不应计入宽度。

即便想通过"从前向后扫描找最后一个有效节点"来修正，也会引入大量细节问题：比如需要逐一遍历每层所有节点、处理全空层的边界情况、区分"中间空节点"和"边缘空节点"等，代码复杂度陡增，还容易出现逻辑漏洞。

问题2：时间/空间复杂度爆炸

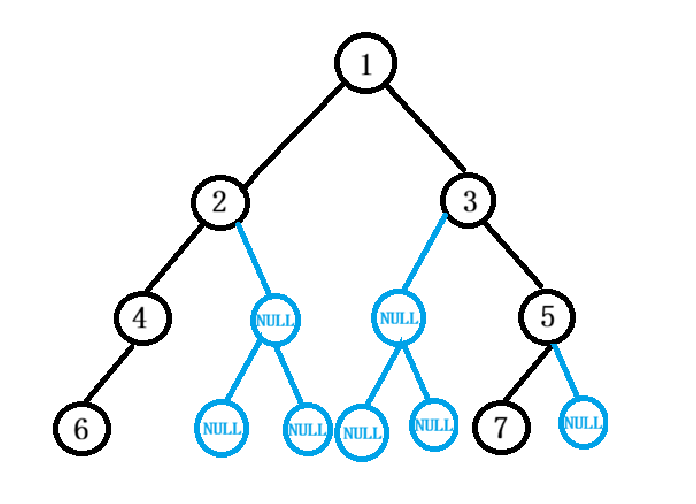
更关键的是，暴力法的复杂度完全不可控。比如遇到这种极端结构：

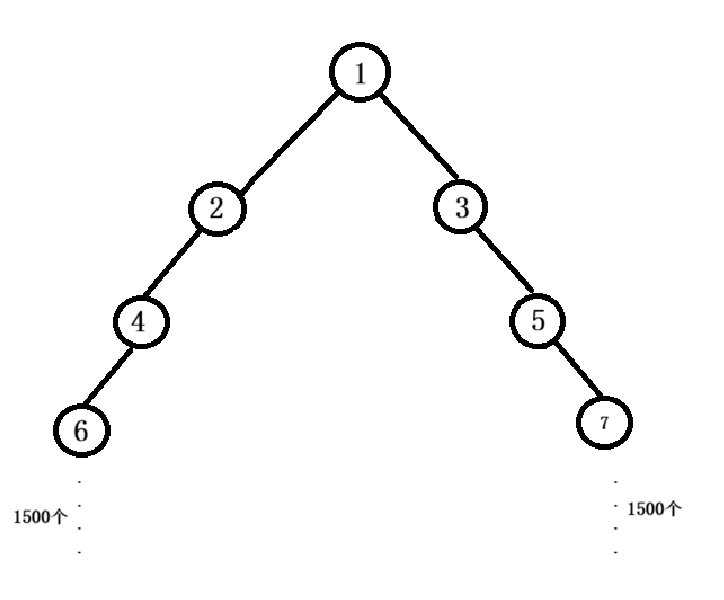
若树的高度达到1500，满二叉树的最后一层节点数是 2¹⁴⁹⁹ 个------这个数量级远超计算机的处理能力，无论是时间还是空间都会直接超限。

所以暴力试图"物理存储所有空节点"来计算宽度，既解决不了空节点边界的逻辑问题，又会因极端场景导致复杂度爆炸，完全不符合题目要求（树节点数最多3000，但暴力法的复杂度和树高呈指数级相关），因此这种思路完全不可取。

利用数组来二叉树，给节点编号

既然暴力法不可行，我们可以换一种思路：利用满二叉树的索引规则标记每个节点的位置，无需存储空节点，仅通过非空节点的索引计算层宽度 。这个思路和 堆的数组实现 原理完全一致，核心是用数学索引代替物理存储。

二叉树节点映射到数组时，左右子节点的索引有固定公式，我们分两种场景：

• 若根节点从下标0 开始：左孩子索引 = 2x + 1，右孩子索引 = 2x + 2；
• 若根节点从下标1 开始：左孩子索引 = 2x，右孩子索引 = 2x + 1。

我们选择从1开始编号（计算宽度时更直观），用这个规则来解决问题：

1. 构建一个队列，队列中存储pair<节点指针, 节点编号>的键值对，将节点和其唯一编号绑定；
2. 按层遍历二叉树，每一层节点入队时，自动继承父节点的编号规则生成子节点编号，绑定关系如下图：
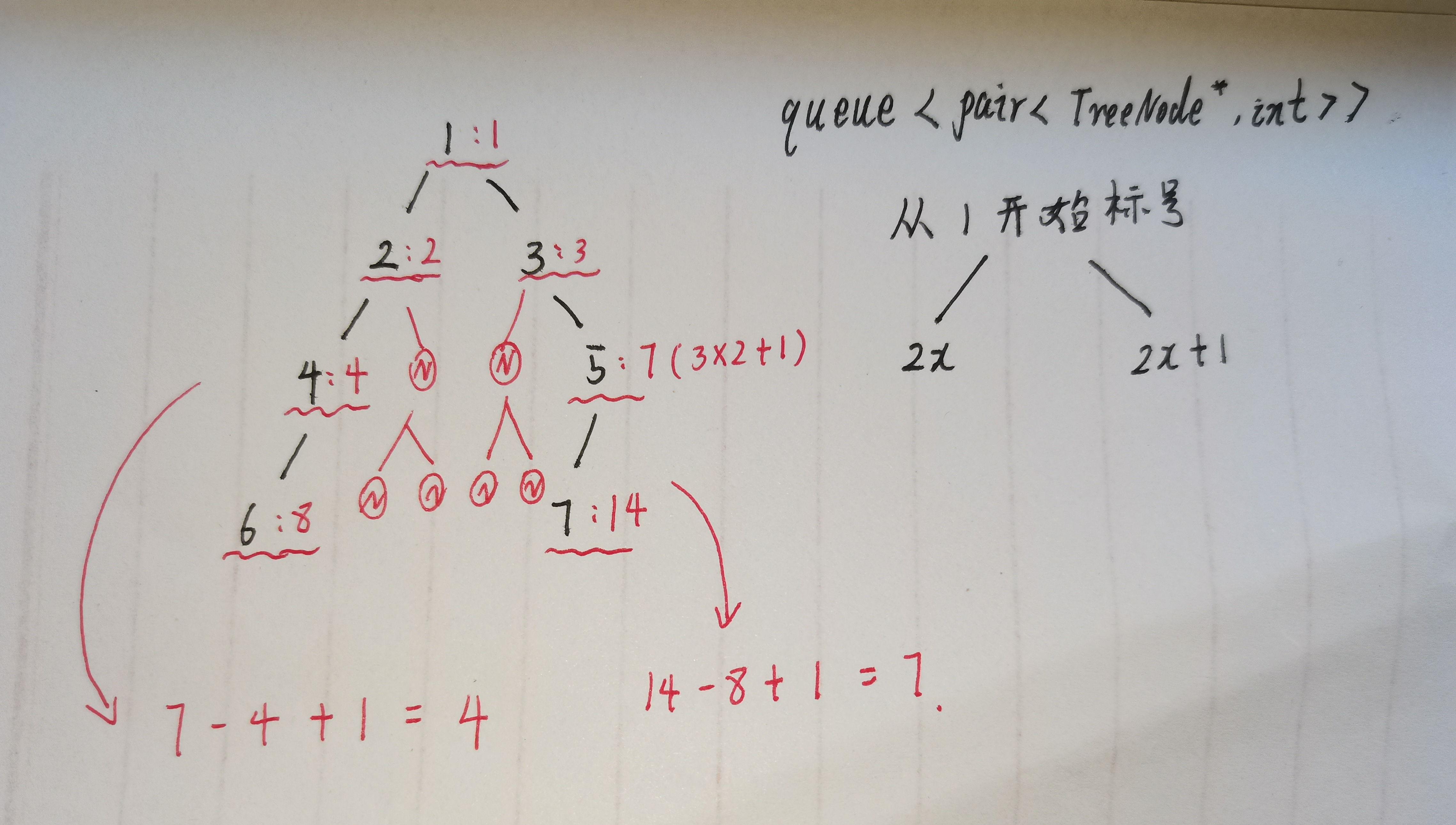
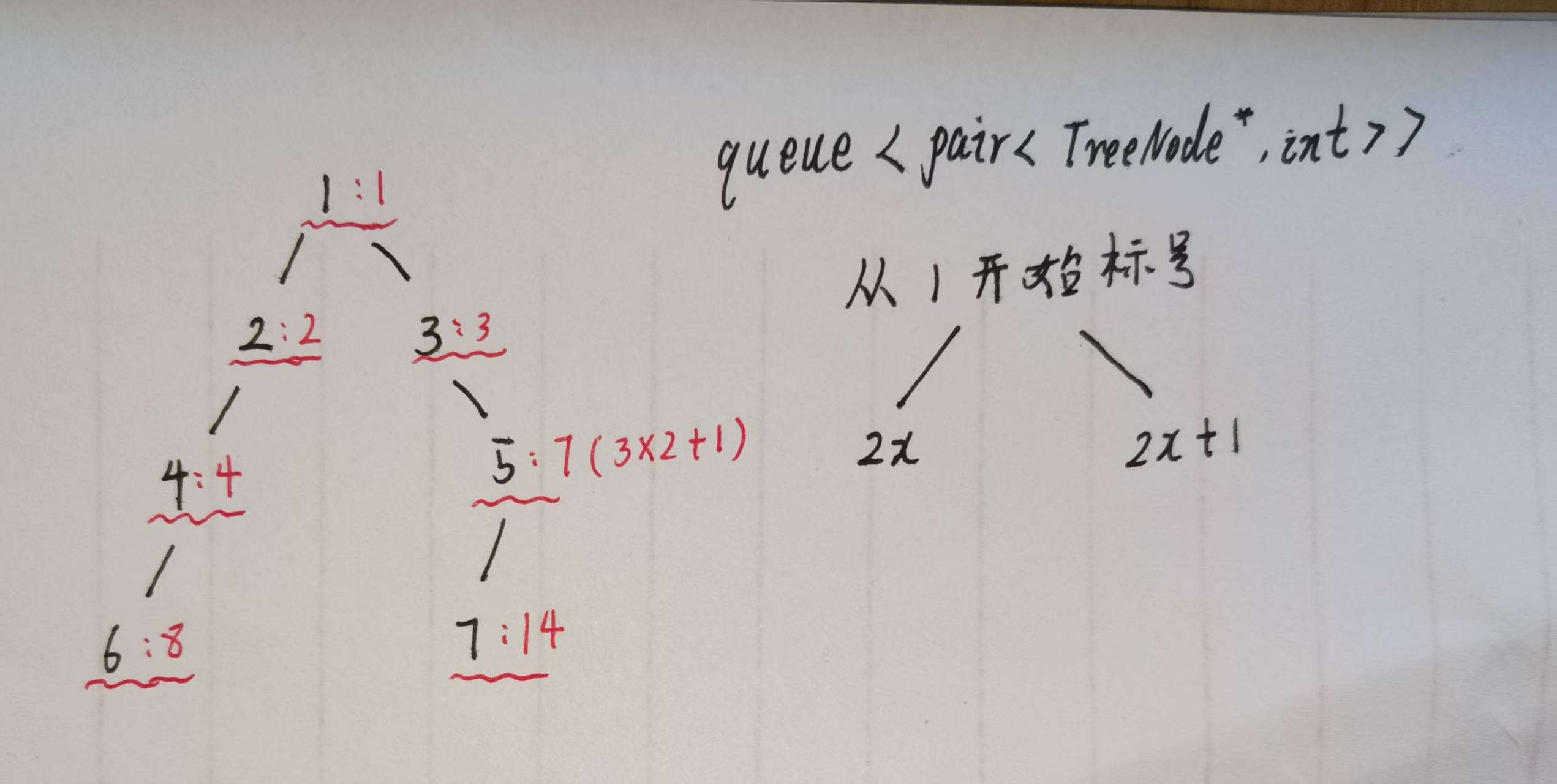   每一层的宽度计算极其简洁：只需取出当前层队列中第一个节点的编号（最左） 和最后一个节点的编号（最右） ，两者做差后加1，就是该层包含空节点的真实宽度，如下图：
   

细节注意

1. 索引溢出问题（核心易错点）

• 结论：两个下标相减时，即便溢出，结果依然正确（但需避免"套圈"）；
• 原理：C/C++中数值存储是"环形"的（比如char类型：0→127→-128→-1→0）。溢出后虽然下标值不准确，但两个下标之间的相对距离（差值） 保持不变，因此宽度计算结果不受影响（前提是差值未超过数据类型的取值范围，即未"套圈"）；
• 实际处理：题目明确"答案在32位带符号整数范围内"，但C/C++中用int存储编号仍会因y*2/y*2+1操作溢出报错，因此必须用unsigned int（无符号整数）存储索引，避免溢出问题。

当两个下标相减即使溢出结果也是正确的原因是，C/C++中数据存储可以看成环形的，比方说char类型，从0开始一直到127再加-128之后再加加加会变成-1之后在变成0，也就是说虽然会溢出，但是由于是环形并且我们要的是两个下标的距离（做减法），即使溢出成负数不是准确的下标值了但是距离没有改变所以不会受影响（前提是不能被套圈）。

2. 队列的切换：每处理完一层后，需要用一个临时数组存储下一层节点，再将原队列替换为临时数组，确保每次循环只处理当前层的节点。
3. 空节点处理：仅当节点的左/右子节点非空时，才将其加入下一层队列，无需处理空节点，保证遍历效率。
4. 宽度计算 ：每一层的宽度 = 最右索引 - 最左索引 + 1（+1是因为索引是从1开始的闭区间）。

五、代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) 
    {
        // 用vector模拟队列，存储<节点指针, 节点的满二叉树索引>
        vector<pair<TreeNode*, unsigned int>> q;
        q.push_back({root, 1});  // 根节点索引初始化为1
        unsigned int ret = 0;    // 记录最大宽度，用unsigned int避免溢出

        // 层序遍历：只要队列不为空，就处理当前层
        while(q.size())
        {
            // 获取当前层最左和最右节点的索引，计算当前层宽度
            auto& [x1,y1] = q[0];    // 最左节点的<指针,索引>
            auto& [x2,y2] = q.back();// 最右节点的<指针,索引>
            ret = max(ret, y2 - y1 + 1); // 更新最大宽度

            // 存储下一层的节点和索引
            vector<pair<TreeNode*, unsigned int>> tmp;
            for(auto& [x, y] : q)
            {
                // 左子节点索引 = 父节点索引 * 2
                if(x->left) tmp.push_back({x->left, y*2});
                // 右子节点索引 = 父节点索引 * 2 + 1
                if(x->right) tmp.push_back({x->right, y*2+1});
            }
            // 切换到下一层
            q = tmp;
        }  
        return ret;  
    }
};

细节说明

1. 队列的模拟 ：用vector<pair<TreeNode*, unsigned int>>代替STL的queue，既可以方便地访问队首（q[0]）和队尾（q.back()）元素，又能高效遍历当前层的所有节点。
2. 索引类型选择 ：使用unsigned int存储索引，避免二叉树深度较大时，y*2操作导致的类型溢出。
3. 核心逻辑 ：
   • 外层循环：控制层序遍历的进程，每次处理一层节点。
   • 层宽度计算：通过q[0]和q.back()快速获取当前层的左右边界索引，计算宽度并更新最大值。
   • 内层循环：遍历当前层所有节点，将非空的左右子节点和对应的索引加入下一层队列。
4. 空节点处理：仅当子节点非空时才加入队列，避免存储空节点，保证遍历效率。

模拟过程

我们用示例1完整模拟，一起直观理解每一步的节点和索引变化：

初始化：

• 队列 q = [{1,1}]
• 最大宽度 ret = 0

步骤	处理层	队列状态	层最左索引	层最右索引	层宽度	ret更新	下一层队列
1	第1层	[{1,1}]	1	1	1	1	[{3,2}, {2,3}]
2	第2层	[{3,2}, {2,3}]	2	3	2	2	[{5,4}, {3,5}, {9,7}]
3	第3层	[{5,4}, {3,5}, {9,7}]	4	7	4	4	[]

最终最大宽度为4，和示例1的输出一致。

复杂度分析

• 时间复杂度：O(n)。n 是二叉树的节点总数，每个节点仅入队和出队一次，总操作次数为 n。
• 空间复杂度：O(n)。最坏情况下（完美二叉树的最后一层），队列需要存储 n/2 个节点，空间复杂度为 O(n)。

六、下题预告

喵~ 能啃完这道二叉树最大宽度喵，宝子超厉害的喵～😼 要是对遍历过程中还有小疑问喵，或者有更丝滑的解题思路喵，都可以甩到评论区喵，我看到会第一时间把问题给这个博主的喵～

别忘了给这个博主点个赞赞喵、关个注注喵～(๑˃̵ᴗ˂̵)و 你对这个博主的支持就是他继续肝优质算法内容的最大动力啦喵～

下一篇我们一起攻克 力扣 515.在每个树行中找最大值 。我们下道题，不见不散喵～