目录
注意:双指针算法中的指针并不一定是真的语法意义上的指针,在数组中大多数情况下都是直接使用下标充当指针使用。
移动零

**思路:**这道题的本质其实就是将数组划分为两部分,一部分是保持相对顺序的非零元素,一部分是所有的0,对于这类数组划分或者说数组分块的题基本都可以使用双指针来解决。
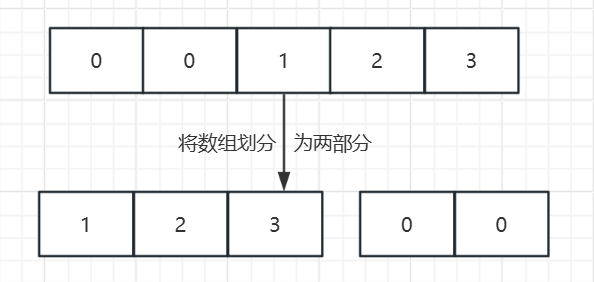
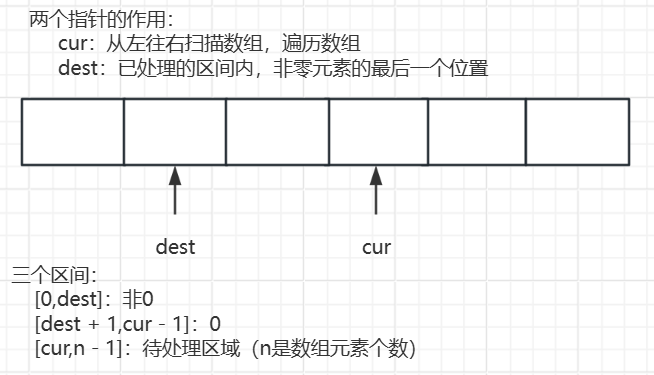
注意:从 [0, cur - 1] 都是已处理区域,[cur, n - 1] 是待处理区域,即 cur 指向所有待处理元素的第一个。(n是数组元素个数)
初始状态:因为一开始待处理区域是整个数组,所以 cur 指向 0 下标位置,dest 用来划分已处理区域中的区间,但是开始时已处理区域为空,所以 dest 指向 -1 下标即可。
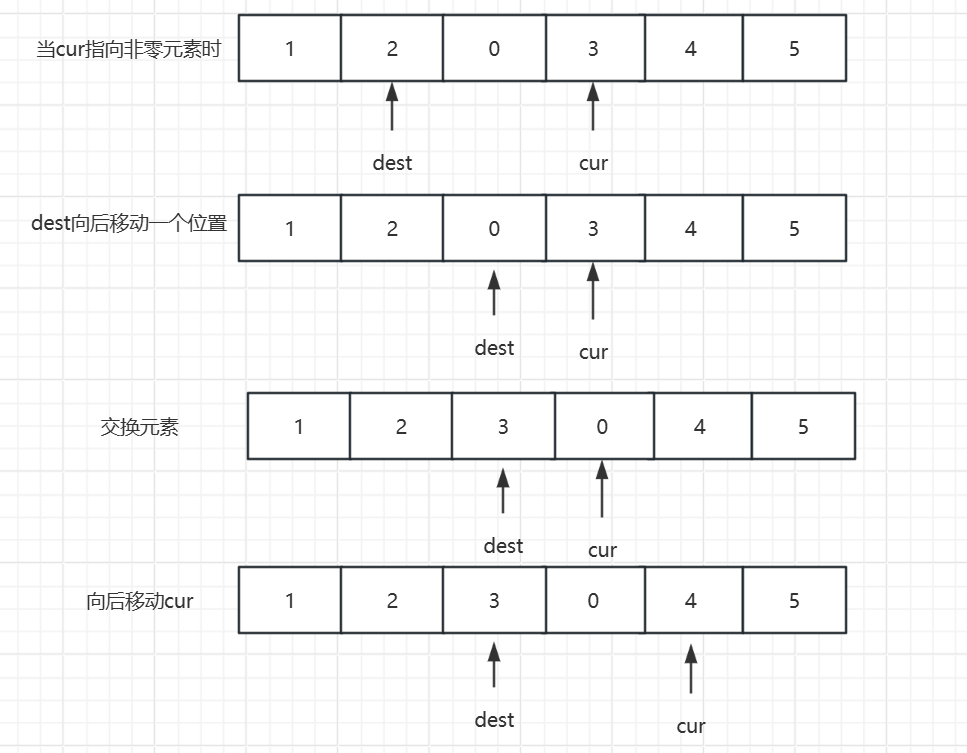
遍历过程:按照上图区间划分,dest 和 cur 中间应该存放元素 0,所以遇到 0 时,dest 指针不动,cur 向后移动即可(这样就将 0 放在它们两个指针中间了),如果不是 0,需要先将 dest 向后移动一个位置,然后交换两指针指向元素,然后cur向后移动一个位置,如图:
代码:
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int dest = -1;
int cur = 0;
while (cur < nums.size()) {
if (nums[cur] != 0) {
dest++;
swap(nums[dest], nums[cur]);
}
cur++;
}
}
};复写零

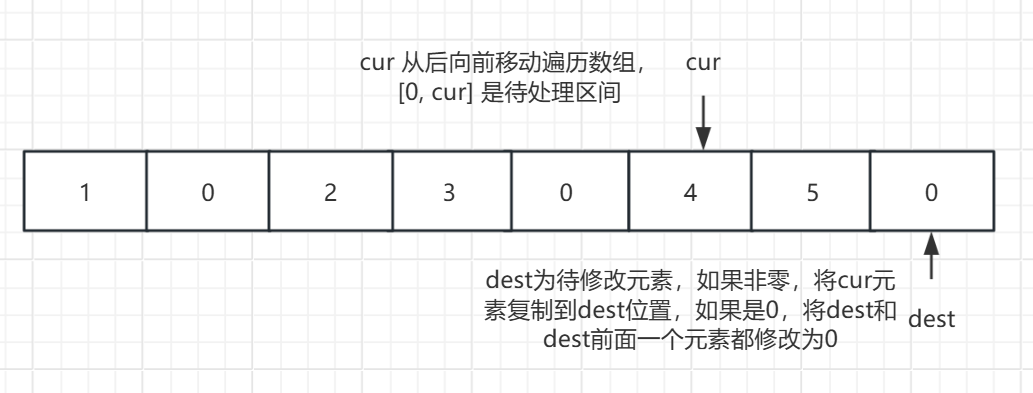
**思路:**这道题的本质就是数组修改,对于这类问题,基本也可以使用双指针解决。但是这道题不可以从左向右遍历数组,因为会覆盖还没有复写的元素,所以需要先找到最后一个复写的数,然后从右向左(即从后向前)完成复写。
- 找到最后一个复写的数
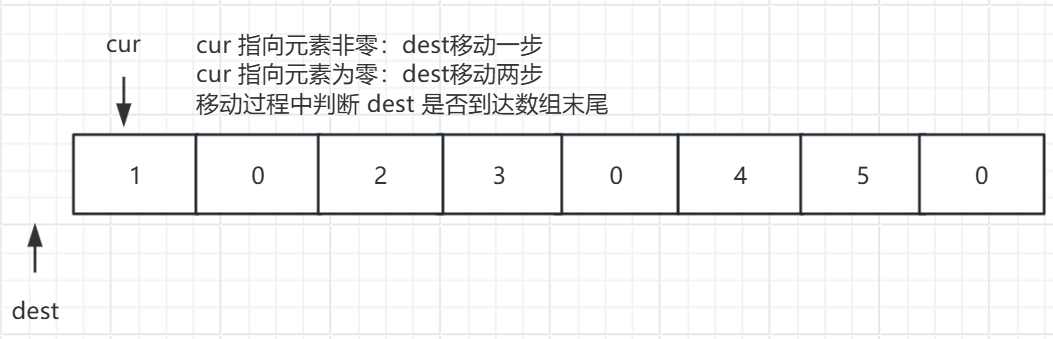
这个问题同样可以使用双指针,定义 cur 指向数组起始位置,定义 dest 指向数组起始位置前一个位置(即-1),然后先判断 cur 位置的值,如果非零,dest 向后移动一步,如果是零,dest 向后移动两步,并且移动过程中判断 dest 是否移动到数组末尾,到末尾遍历结束,cur位置就是最后一个复写的数,否则 cur 继续向后遍历。
- 从后向前复写
- 处理特殊情况
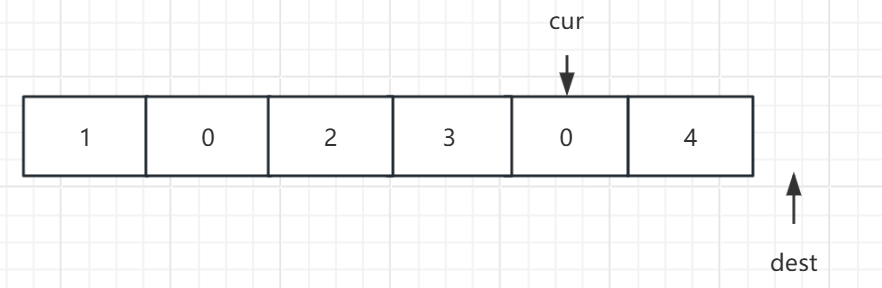
下图这种情况在找最后一个复写的数时会导致数组越界,需要进行特殊处理,可以在找完最后一个复写的数时,判断 dest 位置,如果在下标为 n(数组最后一个元素后一个位置)处,说明出现越界情况,将 n - 1 位置处的元素置 0,然后将 cur 向前移动一位,dest 向前移动两位:
代码:
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int cur = 0;
int dest = -1;
int n = arr.size();
while(cur < n){
if(arr[cur] == 0) dest += 2;
else dest += 1;
if(dest >= n - 1) break;
cur++;
}
if(dest == n){
arr[n - 1] = 0;
cur--;
dest -= 2;
}
while(cur >= 0){
if(arr[cur] == 0){
arr[dest--] = 0;
arr[dest--] = 0;
}
else{
arr[dest--] = arr[cur];
}
cur--;
}
}
};快乐数

**思路:**根据题目描述,按照题中的计算方式最终会有两种情况,要么变为1,要么无限循环且变不到1,即如下图:
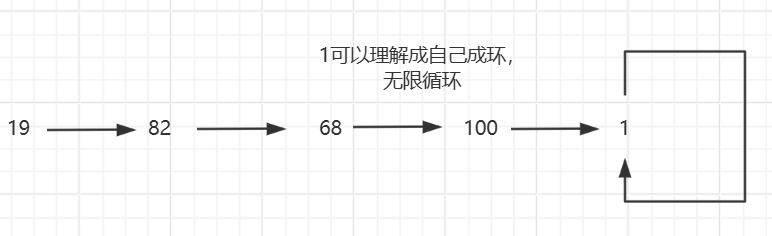
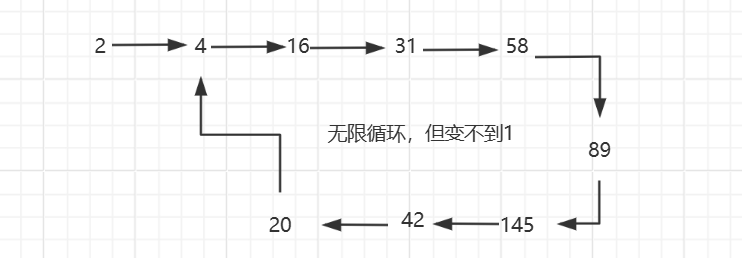
对于这种成环问题,我们可以使用快慢双指针来解决。
代码:
cpp
class Solution {
public:
bool isHappy(int n) {
int slow = squareSum(n);
int fast = squareSum(slow);
while(slow != fast){
slow = squareSum(slow);
fast = squareSum(fast);
fast = squareSum(fast);
}
if(slow != 1){
return false;
}
return true;
}
int squareSum(int n){
int ret = 0;
while(n > 0){
int num = n % 10;
n /= 10;
ret += num * num;
}
return ret;
}
};盛最多水的容器
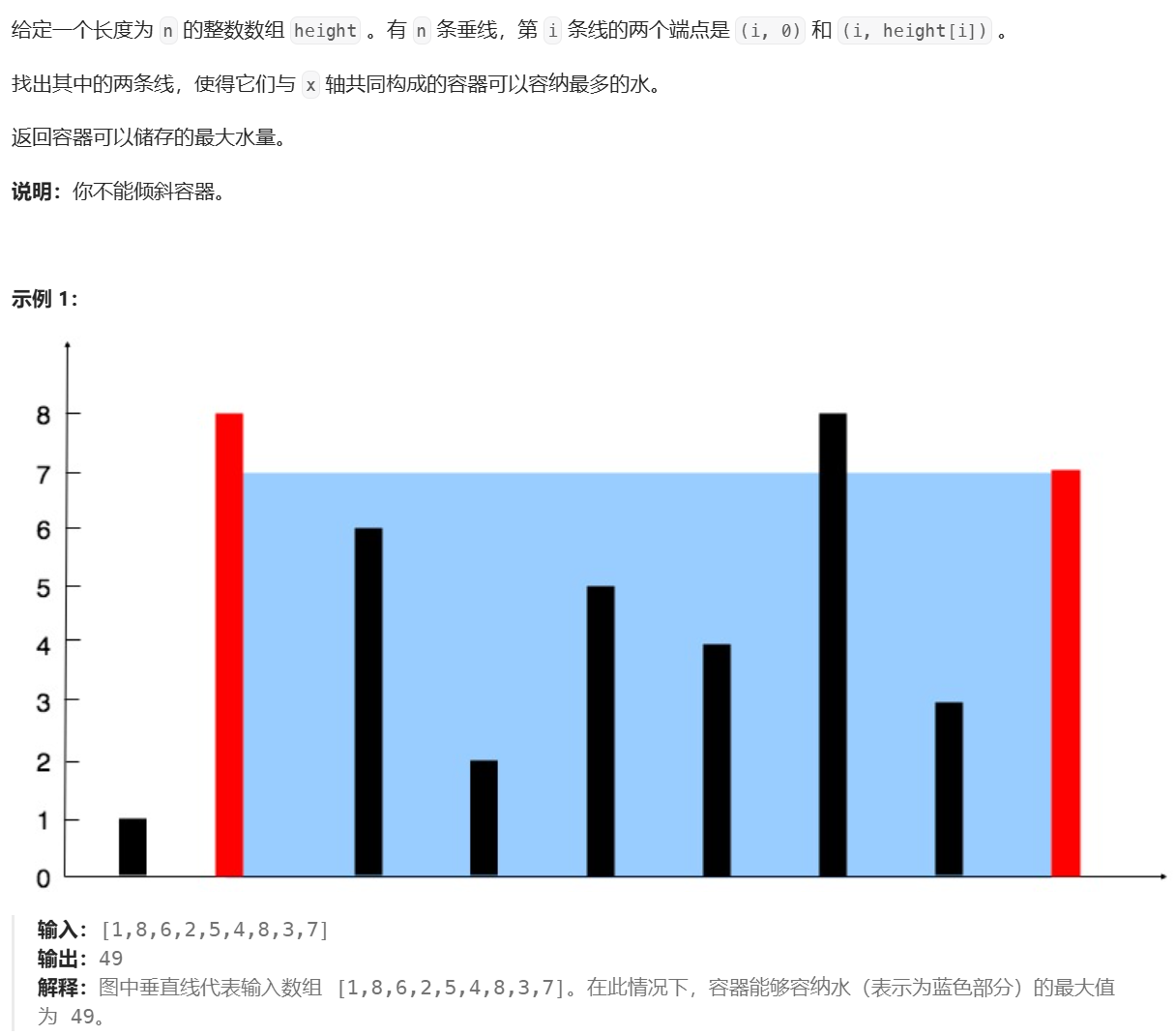
**思路:**使用双指针法。起始时,两个指针分别指向最左边和最右边,然后以短边为高,两指针之间距离为底,计算面积即可,然后移动指向最短边的指针,如果该指针在左边,就向右移动,如果该指针在右边,就向左移动,所有算出的面积中的最大值就是最终答案。
代码:
cpp
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0;
int right = height.size() - 1;
int ret = 0;
while(left < right){
int h = 0;
if(height[left] > height[right]){
h = height[right];
right--;
}
else{
h = height[left];
left++;
}
ret = max(ret, h * (right - left + 1));
}
return ret;
}
};有效三角形的个数

**思路:**先对数组进行排序(方便判断是否符合三角形并且支持使用双指针算法进行优化)。
初始状态:先使用一个指针固定最大的数,在使用一个指针固定次大的数,在使用一个指针固定最小的数。
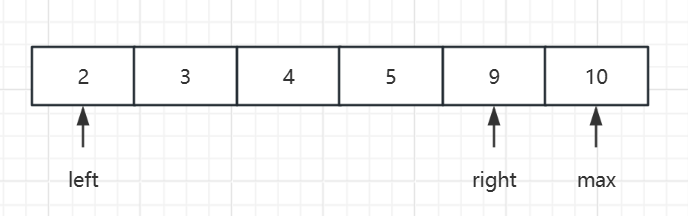
过程:判断 left 所指向的数和 right 所指向的数加和是否大于 max 所指向的数,大于的话 left 以及 left 和 right 之间的数都能和 right,max 所指向的数构成三角形,所以中间的数就没有必要判断了,直接将数字个数算入结果中即可,然后将 right 左移,继续判断,符合就继续向最终结果中加入三角形个数,不符合就向右移动 left,直到符合或者大于等于 right 为止,当 left 和 right 指针移动完一次循环后(即left >= right),将最大值向左移动,继续重复上述 left 和 right 的判断过程,直到 max 所表示的下标小于 2,因为小于 2 时剩余的元素已经不够构成三角形了。
代码:
cpp
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int ret = 0;
int n = nums.size();
for(int i = n - 1; i >= 2; i--){
int left = 0;
int right = i - 1;
while(left < right){
if(nums[left] + nums[right] > nums[i]){
ret += right - left;
right--;
}
else{
left++;
}
}
}
return ret;
}
};查找总价格为目标值的两个商品

**思路:**因为题中给出的数组是有序的,所以可以直接使用两个指针分别指向第一个和最后一个元素,当加和大于目标值时,右边的指针左移一位继续判断即可,当加和小于目标值时,左边的指针右移一位继续判断即可,直到找到一组符合条件的值。(移动指针的目的就是当大于目标值时,将参与运算的最大的数减小,当小于目标值时将参与运算的最小值增大)
代码:
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0;
int right = price.size() - 1;
while(left < right){
if(price[left] + price[right] > target){
right--;
}
else if(price[left] + price[right] < target){
left++;
}
else{
break;
}
}
return {price[left], price[right]};
}
};三数之和

**思路:**排序+双指针+去重。
排序:如果不排序,会出现符合条件的三元组的三个值都相同,但是顺序不同,要去重就需要对每个三元组单独在排序然去重,但是如果先排序在找三元组,值相同的情况下,顺序一定相同,结合容器去重更加方便。
双指针:先定位一个元素,然后使用双指针遍历剩余数据找符合条件的值(这里类似于查找总价值为目标值的两个商品这道题)。
去重:当找到符合条件的值后,移动双指针时直接使用 while 循环跳过相同值即可。除此之外也可以使用unordered_set,它本身就具有去重的效果。
代码:
cpp
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<vector<int>> ret;
for(int i = 0; i < nums.size() - 2; i++){
int left = i + 1;
int right = nums.size() - 1;
int key = 0 - nums[i];
while(left < right){
if(nums[left] + nums[right] > key){
right--;
}
else if(nums[left] + nums[right] < key){
left++;
}
else{
ret.push_back({nums[i], nums[left], nums[right]});
while(left < right && nums[left] == nums[left + 1]) left++;
while(left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
}
}
while(i < nums.size() - 1 && nums[i] == nums[i + 1]) i++; //跳过相同的第一个元素
}
return ret;
}
};四数之和

**思路:**这道题的思路和三数之和一样,只不过三个数变成了四个数,需要两重循环固定两个数,然后再使用双指针,并且本题的目标值是外部给的。
代码:
cpp
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
sort(nums.begin(), nums.end());
vector<vector<int>> ret;
int n = nums.size();
for(int i = 0; i <= n - 4; i++){
for(int j = i + 1; j <= n - 3; j++){
int left = j + 1;
int right = n - 1;
long long key = (long long)target - nums[i] - nums[j];
while(left < right){
if(nums[left] + nums[right] > key) right--;
else if(nums[left] + nums[right] < key) left++;
else{
ret.push_back({nums[i], nums[j], nums[left], nums[right]});
while (left < right && nums[left] == nums[left + 1]) left++;
while (left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
}
}
while(j < n - 3 && nums[j] == nums[j + 1]) j++;
}
while(i < n - 4 && nums[i] == nums[i + 1]) i++;
}
return ret;
}
};