目录

1.摘要
面向AUV在三维复杂海洋环境中的多任务路径规划问题,本文构建以最短路径与最小危险距离为目标的双层多目标模型,并提出ACO+PSO+A *双层混合算法:外层ACO优化任务访问顺序,内层PSO生成航路点并结合A *规划无碰撞路径,通过反馈机制迭代更新信息素以提升解的质量。
2.AUV多任务路径规划模型
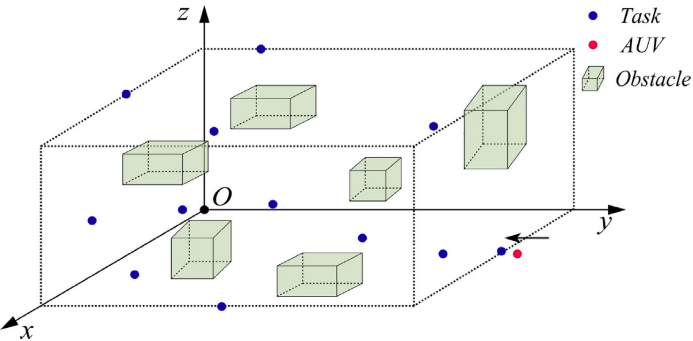
针对三维含障碍海洋环境下AUV多任务路径规划问题,本文将任务点 T T T 与长方体障碍物 O O O 进行空间抽象建模,目标是在避障约束下生成一条遍历全部任务的最短安全路径。为简化求解,假设AUV可视为粒子匀速运动,障碍物与任务点位置已知且固定,每个任务仅访问一次,能量充足目起点终点任务固定。在此基础上,构建双层双目标规划模型:上层为固定起终点的改进TSP,决策任务序列 Q Q Q,目标最小化相邻任务间无碰撞路径的综合评价代价:
min ∑ i = 1 m − 1 C E i ( i + 1 ) \min\sum_{i=1}^{m-1}CE_{i(i+1)} mini=1∑m−1CEi(i+1)
下层在给定任务序列后,为相邻任务 Q i → Q i + 1 Q_i\to Q_{i+1} Qi→Qi+1规划由航路点 q i q_i qi组成的无碰撞路径,同时最小化总路径长度并最大化安全性(航路点到障碍物的最小距离):
{ min ∑ i = 1 m − 1 ∑ j = 1 ∣ q i ∣ − 1 d ( q i j , q i , j + 1 ) max ∑ i = 1 m − 1 min j S ( q i j ) \begin{cases}\min\sum_{i=1}^{m-1}\sum_{j=1}^{|q_i|-1}d(q_{ij},q_{i,j+1})\\\max\sum_{i=1}^{m-1}\min_jS(q_{ij})&\end{cases} {min∑i=1m−1∑j=1∣qi∣−1d(qij,qi,j+1)max∑i=1m−1minjS(qij)
采用曼哈顿距离与单位步长约束
∣ x k − x k + 1 ∣ + ∣ y k − y k + 1 ∣ + ∣ z k − z k + 1 ∣ = 1 |x_k-x_{k+1}|+|y_k-y_{k+1}|+|z_k-z_{k+1}|=1 ∣xk−xk+1∣+∣yk−yk+1∣+∣zk−zk+1∣=1
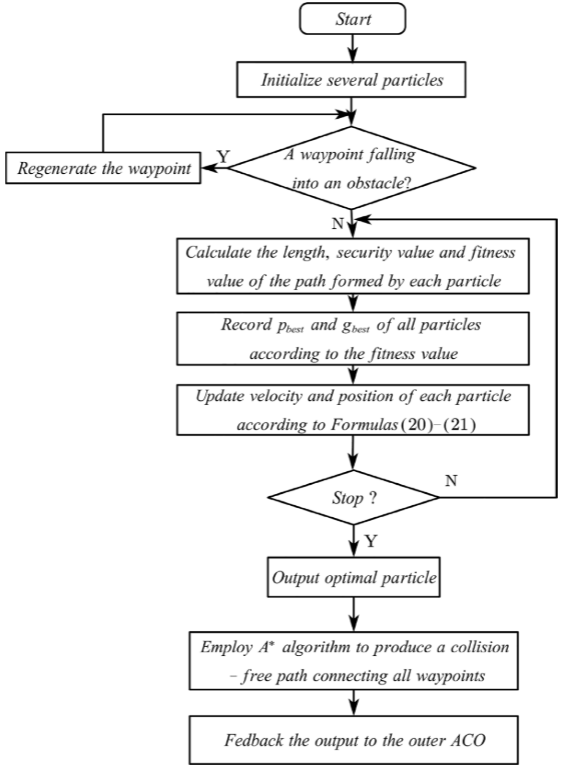
3.双层混合算法
外部蚁群算法
外层ACO部分基于最大最小蚁群系统(MMAS)思想:用综合评价(同时考虑路径长度与安全性)作为启发信息,利用信息素与启发因子共同决定任务转移概率,并引入精英策略优先强化当前最优解以加速收敛。为兼顾搜索范围与收敛速度,论文还设计了自适应信息素挥发机制:前期增强探索以避免早熟收敛,后期提高优劣路径差异以加快稳定收敛,并通过信息素上下界约束防止算法陷入局部最优。
内部PSO-A*混合算法
内层PSO+A* 混合算法用PSO在相邻任务之间生成少量关键航路点,从而显著缩小可行解空间;再利用A* 在这些航路点之间进行精细搜索,快速得到连接航路点的最优无碰撞路径,实现粗规划+细规划的加速策略。
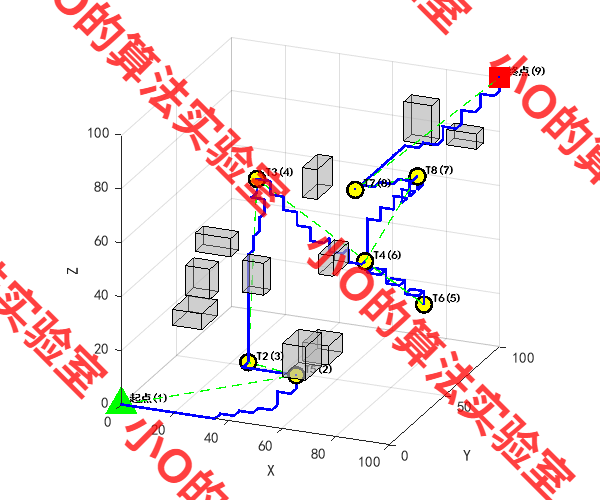
4.结果展示
5.参考文献
1\] Sui F, Tang X, Dong Z, et al. ACO+ PSO+ A\*: A bi-layer hybrid algorithm for multi-task path planning of an AUV\[J\]. Computers \& Industrial Engineering, 2023, 175: 108905. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx