
cpp
bool isPalindrome(string &s, int start, int end) // ✅ 引用传递因为:
-
isPalindrome只是读取字符串,不修改它 -
但最好加上
const:bool isPalindrome(const string &s, ...)
cpp
// 使用 const &,因为不修改字符串,只读取
void backtracking(const string &s, int startIndex)为什么 partition 函数中的 s 不用 &?
cpp
vector<vector<string>> partition(string s) // 这里不用 &调用者传参灵活 :如果这里用 string &s,调用者必须传递一个已有的 string 变量
cpp
string str = "aab";
partition(str); // 需要已有变量可以接受临时对象:不用 & ,即可以接受临时创建的字符串
cpp
partition("aab"); // 临时字符串
partition(string("aab")); // 临时对象
cpp
string str = s.substr(startIndex, i - startIndex + 1);参数说明:
-
startIndex:子串的起始位置(从0开始计数) -
i - startIndex + 1:要提取的字符数量(子串的长度)
cpp
s.substr(startIndex); // 提取从startIndex到字符串末尾的所有字符
cpp
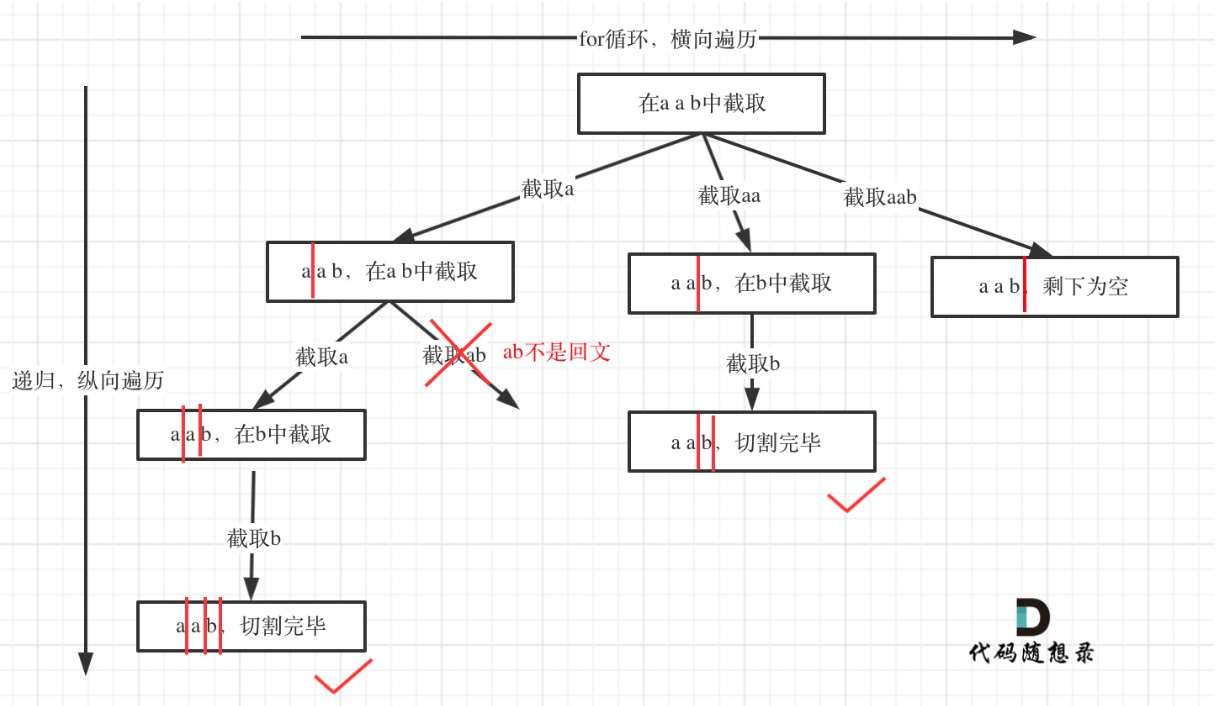
s.substr(); // 提取整个字符串从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么**[startIndex, i] 就是要截取的子串**。
所以子串的长度为i - startIndex+1
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
cpp
class Solution {
private:
vector<vector<string>> result; // 存储所有可能的分割方案
vector<string> path; // 存储当前分割方案中的回文子串
void backtracking (const string& s, int startIndex) {
// 如果起始位置已经大于等于s的长度,说明已经分割到字符串末尾
if (startIndex >= s.size()) {
result.push_back(path); // 将当前分割方案加入结果集
return;
}
// 从startIndex开始尝试所有可能的分割点
for (int i = startIndex; i < s.size(); i++) {
// 检查s[startIndex]到s[i]的子串是否是回文
if (isPalindrome(s, startIndex, i)) {
// 获取回文子串
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str); // 将回文子串加入当前路径
} else { // 不是回文,跳过当前分割点
continue;
}
backtracking(s, i + 1); // 递归处理剩余子串,从i+1开始
path.pop_back(); // 回溯:移除最后添加的子串,尝试其他分割可能
}
}
// 判断子串s[start...end]是否是回文
bool isPalindrome(const string& s, int start, int end) {
// 双指针法判断回文
for (int i = start, j = end; i < j; i++, j--) {
if (s[i] != s[j]) {
return false; // 有字符不相等,不是回文
}
}
return true; // 所有字符都对称,是回文
}
public:
vector<vector<string>> partition(string s) {
// 清空结果集和路径,防止多次调用时数据残留
result.clear();
path.clear();
// 从索引0开始回溯分割
backtracking(s, 0);
return result; // 返回所有分割方案
}
};
举一个具体例子,输入:s = "aab",来模拟上述代码流程
初始状态
s = "aab" 调用 partition("aab")
第1步:partition() 函数
result.clear() → result = [] path.clear() → path = [] 调用 backtracking(s, 0)
第2步:backtracking(s, 0)
cppif (startIndex >= s.size()) { result.push_back(path); // 将当前分割方案加入结果集 return; }
startIndex = 0 , s.size() = 3 if (0 >= 3)不满足if语句
cppfor (int i = startIndex; i < s.size(); i++) { // 检查s[startIndex]到s[i]的子串是否是回文 if (isPalindrome(s, startIndex, i)) { // 获取回文子串 string str = s.substr(startIndex, i - startIndex + 1); path.push_back(str); // 将回文子串加入当前路径 } else { // 不是回文,跳过当前分割点 continue; } backtracking(s, i + 1); // 递归处理剩余子串,从i+1开始 path.pop_back(); // 回溯:移除最后添加的子串,尝试其他分割可能 }
for 循环开始:i=0 到 2 现在i=0 调用 isPalindrome(s, 0, 0): 比较 s[0]='a' 和 s[0]='a' → true if (true) → 进入if块 str = s.substr(0, 1) = "a" path.push_back("a") → path = ["a"] 调用 backtracking(s, 1)
第3步:backtracking(s, 1)
startIndex = 1 if (1 >= 3)不满足if条件 执行for循环 for 循环开始:i = 1 到 2 现在i=1 判断if (isPalindrome(s, startIndex, i)) 函数isPalindrome(s, 1, 1): 比较 s[1]='a' 和 s[1]='a' → true if (true) → 所以进入if语句
cppif (isPalindrome(s, startIndex, i)) { // 获取回文子串 string str = s.substr(startIndex, i - startIndex + 1); path.push_back(str); // 将回文子串加入当前路径
str = s.substr(1, 1) = "a"(从s[1]开始,取一个字符) path.push_back("a") → path = ["a", "a"] 调用 backtracking(s, 2)
第4步:backtracking(s, 2)
startIndex = 2 if (2 >= 3)不满足if条件 所以执行for循环 for 循环开始:i = 2 到 2 现在i=2 调用 isPalindrome(s, 2, 2): 比较 s[2]='b' 和 s[2]='b' → true if (true) → 进入if语句 str = s.substr(2, 1) = "b"(从s[2]取1个字符) path.push_back("b") → path = ["a", "a", "b"] 调用 backtracking(s, 3)
第5步:backtracking(s, 3)
startIndex = 3 if (3 >= 3) 满足if语句true → 进入if
cppif (startIndex >= s.size()) { result.push_back(path); // 将当前分割方案加入结果集 return; }
result.push_back(path) → result = [["a", "a", "b"]] return 到上一层(backtracking(s, 2))
第6步:回到 backtracking(s, 2)
cppbacktracking(s, i + 1); // 递归处理剩余子串,从i+1开始 path.pop_back(); // 回溯:移除最后添加的子串,尝试其他分割可能
继续执行 backtracking(s, i+1) 后面的代码: path.pop_back() → 之后path = ["a", "a"] i++ → i=3,不再满足for循环条件,循环结束 return 到上一层(backtracking(s, 1))
第7步:回到 backtracking(s, 1)
// 继续执行 backtracking(s, i+1) 后面的代码: // 这里的 i = 1,因为这是 i = 1 这个循环分支 path.pop_back(); 之前 path = ["a", "a"] pop移除最后一个元素 → 现在path = ["a"]
for 循环继续 i++; // i 从 1 变成 2 检查for循环条件:i < s.size() -> 2 < 3 满足for循环条件true 所以进入for循环:现在i = 2 ,startIndex 仍为 1
cppfor (int i = startIndex; i < s.size(); i++) { // 检查s[startIndex]到s[i]的子串是否是回文 if (isPalindrome(s, startIndex, i)) { // 获取回文子串 string str = s.substr(startIndex, i - startIndex + 1); path.push_back(str); // 将回文子串加入当前路径 } else { // 不是回文,跳过当前分割点 continue; } backtracking(s, i + 1); // 递归处理剩余子串,从i+1开始 path.pop_back(); // 回溯:移除最后添加的子串,尝试其他分割可能 }
调用 isPalindrome(s, 1, 2):(从s[1]开始取2个字符)"ab" 比较 s[1]='a' 和 s[2]='b' → false ("ab"不是回文,返回 false) if (false) → 执行continue i++ → i=3,不满足for循环条件,循环结束。for循环结束后,即backtracking(s, 1)函数执行完毕。所以返回到调用者:backtracking(s, 0) 执行 path.pop_back() → path = ["a"] return 到上一层(backtracking(s, 0))
移除 "a",path = []
continue 语句的作用:
-
跳过当前循环中剩余的代码
-
直接进入下一次循环迭代
-
这意味着:
-
不会执行
backtracking(s, i + 1)(即backtracking(s, 3)) -
不会执行这个分支的
path.pop_back() -
直接进入
i++
-
第8步:回到 backtracking(s, 0)
path.pop_back(); 之前前 path = ["a"],现在移除最后一个元素,现在path = [] i = 0 的循环结束 i++ → 现在i = 1 调用 isPalindrome(s, 0, 1): 比较 s[0]='a' 和 s[1]='a' → true if (true) → 进入if语句 str = s.substr(0, 2) = "aa" path.push_back("aa") → path = ["aa"] 调用 backtracking(s, 2)
第9步:backtracking(s, 2)
startIndex = 2 if (2 >= 3) 不满足if条件判断 for 循环开始:i = 2 到 2 调用 isPalindrome(s, 2, 2): 比较 s[2]='b' 和 s[2]='b' → true if (true) → 进入if块 str = s.substr(2, 1) = "b" path.push_back("b") → path = ["aa", "b"] 调用 backtracking(s, 3)
.........
.........
.........
.........