《优化算法效率的利器：双指针的原理、变种与边界处理》

**前引：**双指针并非单一的算法模式，而是一套"灵活应变"的解题框架：在数组中，它可以是"左右指针"从两端向中间收缩，解决二分查找、两数之和等问题；在链表中，它可以是"快慢指针"一快一慢移动，定位环的入口或中间节点；在字符串中，它又能变身"滑动窗口指针"，动态维护符合条件的子串范围。这些变种的核心逻辑相通，但细节处理却各有讲究------比如边界条件如何判断、指针移动的触发条件是什么、如何避免数组越界！

【一】数组分块

【一】数组分块

（1）例题

移动零：https://leetcode.cn/problems/move-zeroes

（2）思路

核心思想：双指针分割数组，形成不同的区块，指针不停的运动，区块维持动态平衡

思路：

通过保持：【0,left】为非0元素，【left+1,right-1】为0元素，【right....】为待处理的元素

建立双指针：left = -1（刚开始不知道最后⼀个⾮零元素在什么位置，初始化为-1），right = 0

当right所指向的为0元素，就right++

当right所指为0元素，就left++（因为left刚开始多算了一位），然后交换，right++，继续循环

当right遍历完所有元素，说明分组完毕

（3）代码

cpp 复制代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) 
    {
        int left=-1;
        int right=0;
        while(1)
        {
            //如果right越界说明完毕
            if(right>=nums.size())break;
            //right负责找非0元素
            if(nums[right]==0)
            {
                right++;
            }
            else//此时right找到了非0元素
            {
                left++;
                std::swap(nums[left],nums[right++]);
            }
        }
    }
};

（4）接口：快速交换

上面用到的重要接口：快速交换两个元素

cpp 复制代码

std::swap(void a,void b);

【二】原地复写

（1）例题

复写0：https://leetcode.cn/problems/duplicate-zeros

（2）思路

双指针从左到右是不行的，需要从右到左找到最后一个复写的位置，根据指针指向正常复写

难点：如何找到最后一个复写的位置？

定义指针left =0，right = -1；left负责遍历，right负责根据left指向进行移动

每次先用left判断指向元素，再移动right，如果right没有超标，就再移动left；依此循环

但是需要考虑该情况：如果right超标了，也就是这种情况【1,2,3,0,5】；当left指向0，此时right要超标一位，那么right需要额外调整到下标4的位置（末尾），同时下标4变为0，left再往前移动一位

（3）代码

cpp 复制代码

class Solution {
public:
    void duplicateZeros(vector<int>& arr) 
    {
        //找复写位置
        int left=0;
        int right =-1;
        while(left<arr.size())
        {
            if(arr[left])right++;
            else right+=2;

            if(right>=arr.size()-1)break;
            left++;
        }
        //处理边界
        if(right==arr.size())
        {
            arr[arr.size()-1]=0;
            right-=2;
            left--;
        }
        //开始复写
        while(right>=0)
        {
            if(arr[left])arr[right--]=arr[left--];
            else
            {
               arr[right--]=0;
               arr[right--]=0;
               left--;
            }
        }
    }

【三】快慢指针

（1）例题

快乐数：https://leetcode.cn/problems/happy-number

（2）思路

最常见的思路：每算一个平方和就放入vector s，后面用find看下一个平方和是否为1或者在s里面

但是这种方法因为 find 的缘故会超时（我已经给大家试过了~）

优选：快慢双指针

如何形成快慢？

快指针先跑，慢指针后跑，达到慢指针追快指针来判断是否有环的情况

快慢双指针的核心：如果有环，那么慢指针会有和快指针相等的那一天

此题中，如果是快乐数，那么快指针最终计算也会等于1，慢指针也最终会为1

如果不是，由于有环，快指针一定会有和慢指针相等的情况

（3）代码

cpp 复制代码

class Solution {
public:
    //计算每位平方和
    int Handle(int num)
    {
        int sum =0;
        while(num>0)
        {
            int n = num%10;//获取个位
            sum+=n*n;//算个位的平方和
            num/=10;//除去个位
        }
        return sum;
    }
    bool isHappy(int n) 
    {
        //快追漫
        int slow = n, fast = Handle(n);
        while(slow!=fast)
        {
            slow = Handle(slow);
            fast = Handle(Handle(fast));
        }
        return slow == 1;
    }
};

（4）接口：获取整数的每位

原理：假设有整数 n ，定义中间变量 num

如果 n 先 %10（余数），就会拿到个位，因为个位不可能超过10，即 num = n%10

再用 n /=10（有几个10），就去除了个位，因为如果该数个位是0，那这个数一定是能被10整除的

比如：199

193 %10 = 3 获取余数，也就拿到了个位；再用193 /= 10，拿到193有几个10，也就是19

cpp 复制代码

    int Handle(int num)
    {
        while(num>0)
        {
            int n = num % 10;//获取个位
            num /= 10;//num除去个位
        }
        return sum;
    }

【四】移动碰撞（核心）

（1）例题

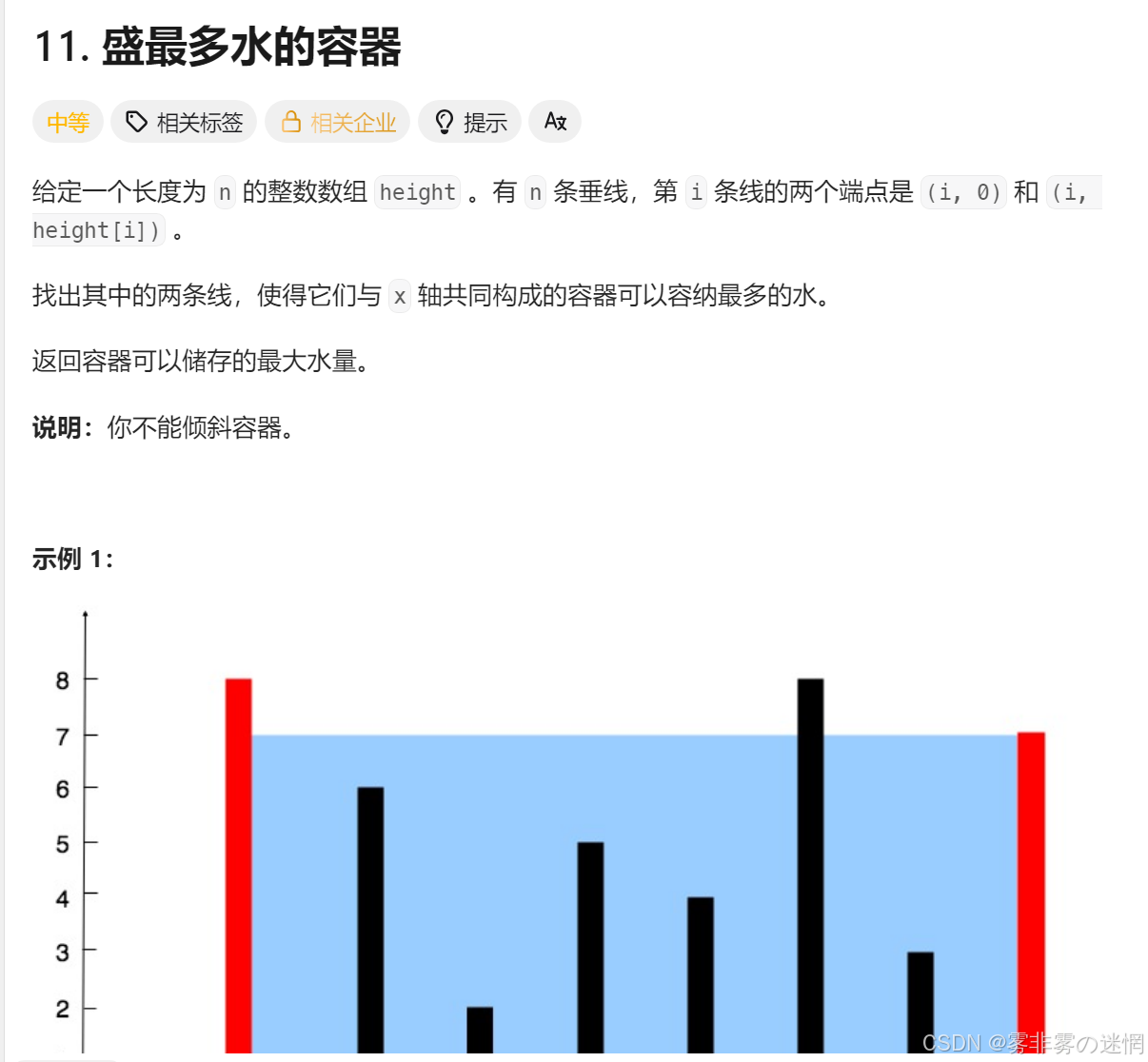
盛水容器：https://leetcode.cn/problems/container-with-most-water

（2）思路

核心：下面开始推理（假设左边界，右边界）

如果左边界不动，右边界慢慢减小，那么宽一定在减小，右边的高只会 <= 左边界

如果右边界不动，左边界慢慢减小，那么宽一定在减小，左边的高只会 <= 右边界

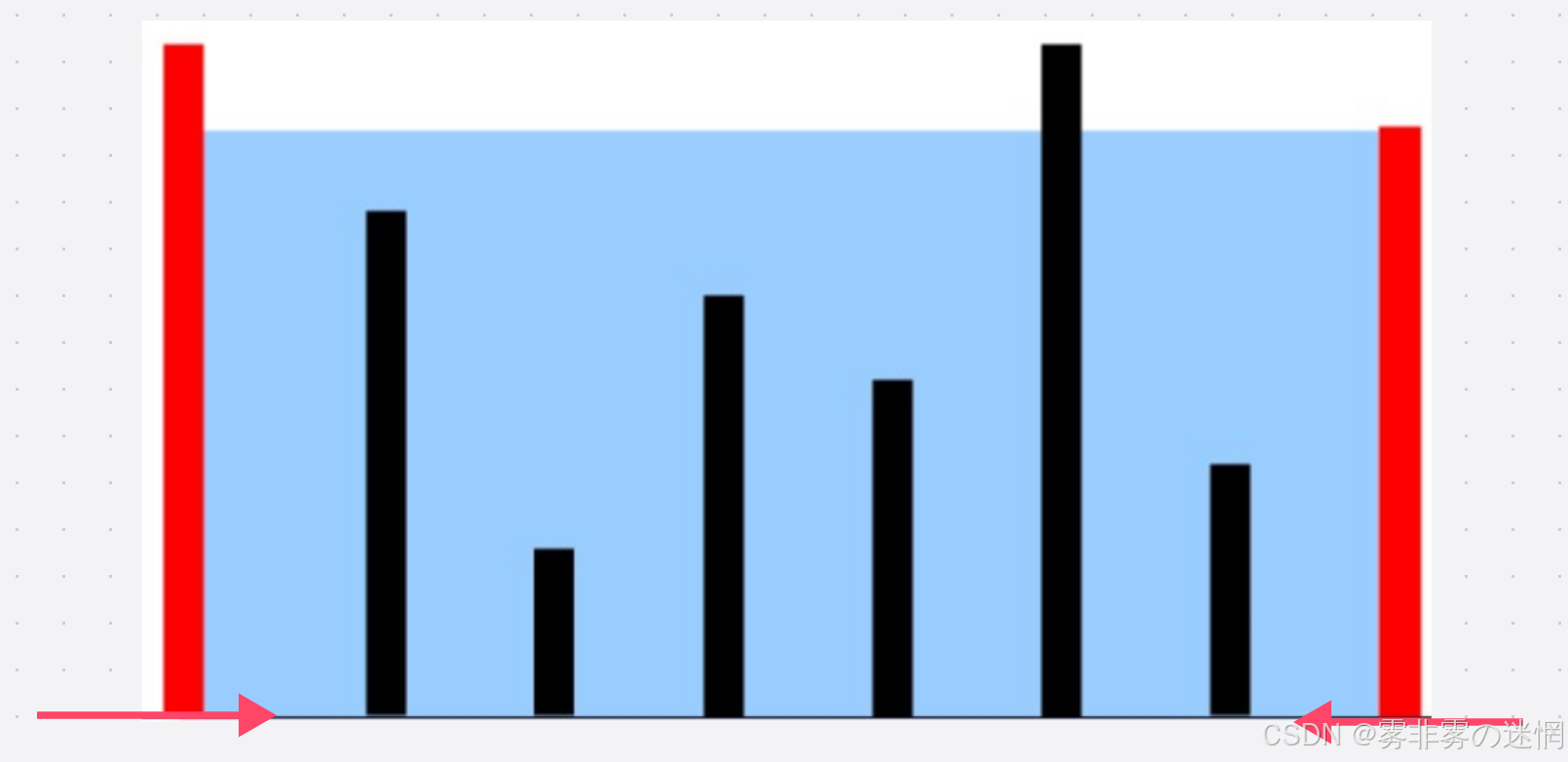
结论：那么只可能两边动态变化，才可以出现最大值，如何动态变化？

如果左边的高小于右边，那么只能以左边的为高，再让左边++，要舍弃高较低的，重新选高

如果左边的高大于右边，那么只能选择右边为高，再让右边--，要舍弃高较低的，重新选高

（理解："你"高那么低，我要你干什么？赶紧走人！我要找高更高的）

（3）代码

cpp 复制代码

class Solution {
public:
    int maxArea(vector<int>& height) 
    {
        int left = 0;
        int right = height.size()-1;
        int high =0;
        int len =0;
        int max=0;
        while(left!=right)
        {
            //算长
            len = right-left;
            //算高(如果右边的高就取左边)
            if(height[left]<height[right])
            {
                high=height[left++];
            }
            else
            {
                high=height[right--];
            }
            //算大小
            if(max>(len*high))continue;
            max=len*high;
        }
        return max;
    }
};

（4）特殊总结

这种双指针移动碰撞的很常见，比如：都是定义一个基准值，再通过移动碰撞解题！有序数组

（例：nums【left】、nums【right】、nums【tmp】,left与right进行与tmp比较,不断缩小范围）

找三角形https://leetcode.cn/problems/valid-triangle-number

求两数之和：https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof

求三数之和：https://leetcode.cn/problems/3sum

（这些题虽然方法一样都是移动碰撞，但是在求三数之和，需要额外考虑去重，可参考下面思路）

cpp 复制代码

#include <vector>
#include <algorithm>
using namespace std;

vector<vector<int>> threeSum(vector<int>& nums) 
{
    vector<vector<int>> res;
    // 1. 排序（必须步骤，为双指针和去重做准备）
    sort(nums.begin(), nums.end());
    int n = nums.size();

    // 2. 固定最左侧指针i，i最多到n-3（保证后面有left和right）
    for (int i = 0; i < n - 2; ++i) 
    {
        // 去重：跳过i位置的重复元素（避免重复三元组）
        if (i > 0 && nums[i] == nums[i-1]) 
        {
            continue;
        }

        int left = i + 1;    // left从i的下一个位置开始（不回头）
        int right = n - 1;   // right从数组末尾开始

        // 3. 双指针向中间收缩
        while (left < right) 
        {
            int sum = nums[i] + nums[left] + nums[right];
            if (sum == 0) 
            {
                // 找到有效三元组，加入结果
                res.push_back({nums[i], nums[left], nums[right]});
                
                // 去重：跳过left位置的重复元素
                while (left < right && nums[left] == nums[left+1]) 
                {
                    left++;
                }
                // 去重：跳过right位置的重复元素（用right-1避免越界）
                while (left < right && nums[right] == nums[right-1])
                {
                    right--;
                }

                // 移动指针，继续寻找下一个可能的组合
                left++;
                right--;
            } 
            // 4. 调整指针：和太小→增大left，和太大→减小right
            else if (sum < 0) 
            {
                left++;
            } else 
            {
                right--;
            }
        }
    }
    return res;
}