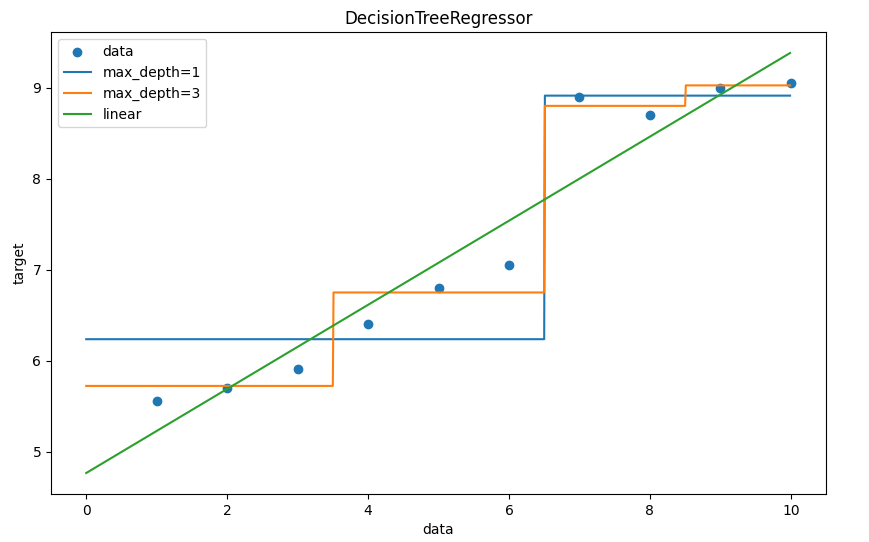
CART 回归决策树
CART 回归树和 CART 分类树的不同之处在于:
• CART 分类树预测输出的是一个离散值,CART 回归树预测输出的是一个连续值
• CART 分类树使用基尼指数作为划分、构建树的依据,CART 回归树使用平方损失
• 分类树使用叶子节点多数类别作为预测类别,回归树则采用叶子节点里均值作为预测输出
CART 回归树的平方损失:
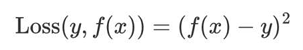
例:根据平方损失,构建CART 回归树
• 已知:数据集只有 1 个特征 x, 目标值值为 y

• 分析:因只有 1 个特征,所以只需选择该特征的最优划分点,并不需要计算其他特征。
1 先将特征 x 的值排序,并取相邻元素均值作为待划分点,如下图所示:

2 计算每一个划分点的平方损失
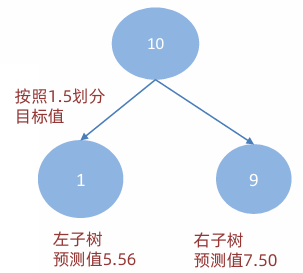
划分点 1.5
(1)R1 为小于 1.5 的样本个数,样本数量为:1,其输出值为:5.56 R1 = 5.56
(2)R2 为大于 1.5 的样本个数,样本数量为:9,其输出值为: R2 = (5.7 + 5.91 + 6.4 + 6.8 + 7.05 + 8.9 + 8.7 + 9 + 9.05) / 9 = 67.51 / 9 = 7.50
(3)该划分点的平方损失: L(1.5) = (5.56 - 5.56)² + [(5.7 - 7.50)² + (5.91 - 7.50)² + (6.4 - 7.50)² + (6.8 - 7.50)² + (7.05 - 7.50)² + (8.9 - 7.50)² + (8.7 - 7.50)² + (9 - 7.50)² + (9.05 - 7.50)²] = 0 + [(-1.8)² + (-1.59)² + (-1.1)² + (-0.7)² + (-0.45)² + (1.4)² + (1.2)² + (1.5)² + (1.55)²] = 0 + [3.24 + 2.5281 + 1.21 + 0.49 + 0.2025 + 1.96 + 1.44 + 2.25 + 2.4025] = 15.72
划分点 2.5
(1)R1 为小于 2.5 的样本个数,样本数量为:2,其输出值为: R1 = (5.56 + 5.7) / 2 = 5.63
(2)R2 为大于 2.5 的样本个数,样本数量为:8,其输出值为: R2 = (5.91 + 6.4 + 6.8 + 7.05 + 8.9 + 8.7 + 9 + 9.05) / 8 = 61.81 / 8 = 7.73
(3)该划分点的平方损失: L(2.5) = [(5.56 - 5.63)² + (5.7 - 5.63)²] + [(5.91 - 7.73)² + (6.4 - 7.73)² + (6.8 - 7.73)² + (7.05 - 7.73)² + (8.9 - 7.73)² + (8.7 - 7.73)² + (9 - 7.73)² + (9.05 - 7.73)²] ≈ 12.07
划分点 3.5
(1)R1 为小于 3.5 的样本个数,样本数量为:3,其输出值为: R1 = (5.56 + 5.7 + 5.91) / 3 = 17.17 / 3 = 5.72
(2)R2 为大于 3.5 的样本个数,样本数量为:7,其输出值为: R2 = (6.4 + 6.8 + 7.05 + 8.9 + 8.7 + 9 + 9.05) / 7 = 56.9 / 7 = 8.13
(3)该划分点的平方损失: L(3.5) = [(5.56 - 5.72)² + (5.7 - 5.72)² + (5.91 - 5.72)²] + [(6.4 - 8.13)² + (6.8 - 8.13)² + (7.05 - 8.13)² + (8.9 - 8.13)² + (8.7 - 8.13)² + (9 - 8.13)² + (9.05 - 8.13)²] ≈ 8.36
,,,,,,,,,,,,,,,,,
3 以此方式计算 2.5、3.5... 等划分点的平方损失,结果如下所示:

4 当划分点 s=6.5时,m(s) 最小。所以第1个划分变量:特征为 X, 切分点为 6.5
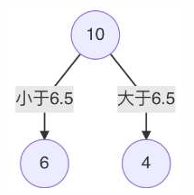
5 对左子树的 6 个节点计算每个划分点的平方式损失,找出最优划分点
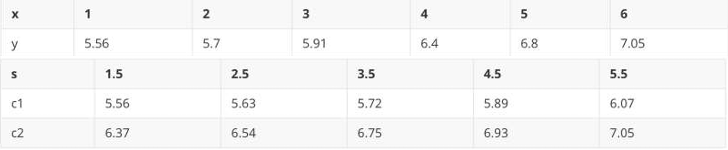
eg:以x=1.5作为切分点,左子树c1输出为5.56,右子树c2输出 (5.7+5.91+6.4+6.8+7.05)/5 = 6.37,L(1.5) = (5.56 - 5.56)² + [(5.7 - 6.572)² + (5.91 - 6.572)² + (6.4 - 6.572)² + (6.8 - 6.572)² + (7.05 - 6.572)²] = 1.3087
以x=2.5作为切分点,左子树c1输出为 (5.56 + 5.7) / 2 = 11.26 / 2 = 5.63,右子树c2输出 (5.91 + 6.4 + 6.8 + 7.05) / 4 = 26.16 / 4 = 6.54,L(2.5) = [(5.56 - 5.63)² + (5.7 - 5.63)²] + [(5.91 - 6.54)² + (6.4 - 6.54)² + (6.8 - 6.54)² + (7.05 - 6.54)²] = 0.754
以x=3.5作为切分点,左子树c1输出为(5.56 + 5.7 + 5.91) / 3 = 17.17 / 3 = 5.7233,右子树c2输出 (6.4 + 6.8 + 7.05) / 3 = 20.25 / 3 = 6.75,L(3.5) = [(5.56 - 5.7233)² + (5.7 - 5.7233)² + (5.91 - 5.7233)²] + [(6.4 - 6.75)² + (6.8 - 6.75)² + (7.05 - 6.75)²] = 0.2771
,,,,,,,,,

6 s=3.5时,m(s) 最小,所以左子树继续以 3.5 进行分裂
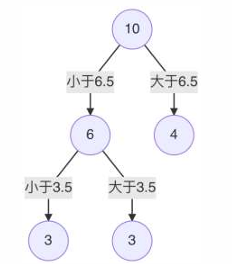
7 假设在生成3个区域之后停止划分,以上就是最终回归树。
每一个叶子节点的输出为:挂在该节点上的所有样本均值。
CART 回归树构建过程小结
• 1 选择一个特征,将该特征的值进行排序,取相邻点计算均值作为待划分点
• 2 根据所有划分点,将数据集分成两部分:R1、R2
• 3 R1 和 R2 两部分的平方损失相加作为该切分点平方损失
• 4 取最小的平方损失的划分点,作为当前特征的划分点
• 5 以此计算其他特征的最优划分点、以及该划分点对应的损失值
• 6 在所有的特征的划分点中,选择出最小平方损失的划分点,作为当前树的分裂点
代码
python
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
def dm01():
# 2.准备数据
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
print('x -->', x)
print('y -->', y)
# 3.模型训练,实例化模型
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=2)
model3 = LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)
# 4.模型预测 # 等差数组-按照间隔
# 0~10, 步长0.01
x_test = np.arange(0.0, 10.0, 0.01).reshape(-1, 1)
print('x_test --> ', x_test[:2])
print('len(x_test) --> ', len(x_test))
y_pre1 = model1.predict(x_test)
y_pre2 = model2.predict(x_test)
y_pre3 = model3.predict(x_test)
print(y_pre1.shape, y_pre2.shape, y_pre3.shape)
# 5.结果可视化
plt.figure(figsize=(10, 6), dpi=100)
plt.scatter(x, y, label='data')
plt.plot(x_test, y_pre1, label='max_depth=1') # 深度1层
plt.plot(x_test, y_pre2, label='max_depth=3') # 深度3层
plt.plot(x_test, y_pre3, label='linear')
plt.xlabel('data')
plt.ylabel('target')
plt.title('DecisionTreeRegressor')
plt.legend()
plt.show()
dm01()执行结果
python
x --> [[ 1]
[ 2]
[ 3]
[ 4]
[ 5]
[ 6]
[ 7]
[ 8]
[ 9]
[10]]
y --> [5.56 5.7 5.91 6.4 6.8 7.05 8.9 8.7 9. 9.05]
x_test --> [[0. ]
[0.01]]
len(x_test) --> 1000
(1000,) (1000,) (1000,)决策树正则化 -- 剪枝
为什么要剪枝?
• 决策树剪枝是一种防止决策树过拟合的一种正则化方法;提高其泛化能力。
剪枝
• 把子树的节点全部删掉,使用用叶子节点来替换
剪枝方法
1.预剪枝 指在决策树生成过程中,对每个节点在划分前先进行估计,若当前节点的划分不能带来决策树泛化性能提升,则停止划分并将当前 节点标记为叶节点;
2.后剪枝 是先从训练集生成一棵完整的决策树,然后自底向上地对非叶节点进行考察,若将该节点对应的子树替换为叶节点能带来决策树泛 化性能提升,则将该子树替换为叶节点。

代码
关键点说明:
预剪枝参数:
max_depth:树的最大深度
min_samples_split:节点最小样本数(少于该值不分裂)
min_samples_leaf:叶节点最小样本数
min_impurity_decrease:分裂带来的纯度提升阈值
后剪枝:
使用 cost_complexity_pruning_path() 计算剪枝路径
通过 ccp_alpha 参数控制剪枝强度(alpha越大,剪枝越强)
通常需要通过交叉验证选择最优的 ccp_alpha
python
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载数据
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=42)
# 1. 预剪枝(通过参数提前停止树的生长)
pre_pruning_tree = DecisionTreeClassifier(
max_depth=2, # 树的最大深度
min_samples_split=5, # 节点最少样本数才能继续划分
min_samples_leaf=3, # 叶节点最少样本数
max_leaf_nodes=10, # 最大叶节点数
min_impurity_decrease=0.01, # 划分增益阈值
random_state=42
)
# 训练模型
pre_pruning_tree.fit(X_train, y_train)
# 预测
y_pred_pre = pre_pruning_tree.predict(X_test)
# 计算预测准确率
accuracy_pre = accuracy_score(y_test, y_pred_pre)
train_pred_pre = pre_pruning_tree.predict(X_train)
train_acc_pre = accuracy_score(y_train, train_pred_pre)
print(f"\n预剪枝模型准确率: {accuracy_pre:.4f}")
# 2. 后剪枝(CCP剪枝方法)
full_tree = DecisionTreeClassifier(random_state=42) # 先创建完整树
full_tree.fit(X_train, y_train)
# 计算CCP路径
path = full_tree.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas = path.ccp_alphas
# 选择最优alpha进行剪枝(通过交叉验证)
post_pruning_tree = DecisionTreeClassifier(ccp_alpha=ccp_alphas[1]) # 选择alpha值
# 训练模型
post_pruning_tree.fit(X_train, y_train)
# 预测
y_pred_post = post_pruning_tree.predict(X_test)
# 计算预测准确率
accuracy_post = accuracy_score(y_test, y_pred_post)
print(f"后剪枝模型准确率: {accuracy_post:.4f}")
train_pred_post = post_pruning_tree.predict(X_train)
train_acc_post = accuracy_score(y_train, train_pred_post)
# 判断是否过拟合
if train_acc_pre - accuracy_pre > 0.1: # 训练集比测试集高10%以上
print("⚠️ 预剪枝模型可能过拟合了!")
if train_acc_post - accuracy_post > 0.1:
print("⚠️ 后剪枝模型可能过拟合了!")
# 关键点说明:
#
# 预剪枝参数:
# max_depth:树的最大深度
# min_samples_split:节点最小样本数(少于该值不分裂)
# min_samples_leaf:叶节点最小样本数
# min_impurity_decrease:分裂带来的纯度提升阈值
#
# 后剪枝:
# 使用 cost_complexity_pruning_path() 计算剪枝路径
# 通过 ccp_alpha 参数控制剪枝强度(alpha越大,剪枝越强)
# 通常需要通过交叉验证选择最优的 ccp_alpha执行结果
预剪枝模型准确率: 0.9778
后剪枝模型准确率: 1.0000