💗博主介绍:计算机专业的一枚大学生 来自重庆 @燃于AC之乐✌专注于C++技术栈,算法,竞赛领域,技术学习和项目实战✌💗
💗根据博主的学习进度更新(可能不及时)
💗后续更新主要内容:C语言,数据结构,C++、linux(系统编程和网络编程)、MySQL、Redis、QT、Python、Git、爬虫、数据可视化、小程序、AI大模型接入,C++实战项目与学习分享。
👇🏻 精彩专栏 推荐订阅👇🏻
🌟算法相关题目点击即可进入实操🌟
感兴趣的可以先收藏起来,请多多支持,还有大家有相关问题都可以给我留言咨询,希望希望共同交流心得,一起进步,你我陪伴,学习路上不孤单!
文章目录
前言
这些题目摘录于洛谷,好题,典型的题,考察各类算法运用,可用于蓝桥杯及各类算法比赛备战,算法题目练习,提高算法能力,补充知识,提升思维。
锻炼解题思路,从学会算法模板后,会分析,用到具体的题目上。
对应题目点链接即可做。
本期涉及算法:bfs暴搜求最短路,动态规划--最长上升子序列模型,二分答案,模拟,贪心 + 扩展域并查集。
题目清单
1.Metoer Shower(流星雨)

题目: P2895 [USACO08FEB] Meteor Shower S

解法:bfs暴搜求最短路
可以看成一个在地图中"走迷宫"的问题,每一步的代价就是花费时间t = 1, 障碍(非法)就是这个时间被已经或刚好被砸了。
现予处理出所有流星雨,记录每个位置最早被击中的时间。 bfs暴搜出所有的路径, 判断 dist[x] [y] < t[x] [y] 才合法。结束判断,第一个搜索到没有被摧毁的位置(安全位置)时,即为结果(最短时间)。
细节: 1.边界:起始位置可能就安全,为结果,需要特判;
2.bfs用queue,每个点坐标x,y,用q.push(pair{x, y})加入队列;
3.要的是最短t, 用min, 数组初t始化为正无穷;
4.bfs时,剪枝:
a. x < 0, y < 0, 超过边界,剪枝;
b.dist[x] [y]!= INF, 已经走过了,更新过了,剪枝;
c. dist[x] [y] + 1 >= t[x] [y], 不合法,剪枝;
5.起始位置,dist[0] [0]初始化为0。
代码:
cpp
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
int m, INF = 0x3f3f3f3f;
const int N = 310;
int t[N][N]; //记录位置[i, j]最早被摧毁时刻
int dist[N][N]; //记录到[i, j]的时间花费
//方向向量
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
int bfs()
{
if(t[0][0] == INF) return 0; //边界处理,开始就安全
memset(dist, 0x3f, sizeof dist);
queue<pair<int, int>> q;
q.push({0, 0});
dist[0][0] = 0;
while(q.size())
{
auto a = q.front(); q.pop();
int i = a.first, j = a.second;
//向四周扩展
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if(x < 0 || y < 0) continue; //非法剪枝
if(dist[x][y] != INF) continue; //被更新过了,重复性剪枝
if(dist[i][j] + 1 >= t[x][y]) continue; //非法剪枝
dist[x][y] = dist[i][j] + 1;
if(t[x][y] == INF) return dist[x][y]; //安全位置
q.push({x, y});
}
}
return -1;
}
int main()
{
cin >> m;
memset(t, 0x3f, sizeof t);
for(int i = 1; i <= m; i++)
{
int x, y, z;
cin >> x >> y >> z;
t[x][y] = min(t[x][y], z);
//周围被摧毁
for(int k = 0; k < 4; k++)
{
int i = x + dx[k], j = y + dy[k];
if(i < 0 || j < 0) continue; //防越界
t[i][j] = min(t[i][j], z);
}
}
cout << bfs() << endl;
return 0;
}2.打鼹鼠


解法:动态规划--最长上升子序列模型

首先,类比上一道题很相似,这道题很具有迷惑性,感觉可以预处理出所有的地鼠(x, y)出来的t,再用bfs/dfs/路径dp,进行走图。
但是,这道题目有一个点,可以自由选定机器人的初始位置,就是起始位置不定,就算是只枚举地鼠出现的位置作为起始位置进行暴搜,时间复杂度也会超,最差情况达到O(n * m * m)。
既然上面的方法行不通,那么再仔细读题,发现有个很重要的点,t 按不降的顺序给出 ,启发,同时由题意,不难得出,先出现的地鼠需要优先处理,后出现的地鼠后处理,且要处理区间的地鼠最多 ,又满足t递增 。那么可以想到最长上升子序列的模型,用动态规划解决。
1.状态表示:
f [i ] 表示:如果消灭的最后一只是i 位置鼹鼠时,最长能消灭多少鼹鼠。
结果确定: f表里面的最大值就是我们要的结果。
2.状态转移方程:
对于f [i],可以划分为两种情况:
只消灭这一只鼹鼠,此时f [i] = 1;
这只鼹鼠放在前面某只鼹鼠j (1 ≤ j < i)后面一起消灭,此时需要满足
abs (x [i ] − x [j ]) + abs (y [i ] −y [j ]) ≤ t [i ] −t [j ],也就是曼哈顿距离小于等于时间差,那么 f [i ] = f [j] + 1。求出所有符合要求的最大值即可。
3.初始化:
这里不需要初始化,直接填表即可。
4.填表顺序:
从左往右。
时间复杂度: O(m * m)。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e4 + 10;
int n, m;
int t[N], x[N], y[N];
int f[N];
int main()
{
cin >> n >> m;
int ret = 0;
for(int i = 1; i <= m; i++)
{
cin >> t[i] >> x[i] >> y[i];
f[i] = 1;
for(int j = 1; j < i; j++)
{
if(t[i] - t[j] >= abs(x[i] - x[j]) + abs(y[i] - y[j]))
{
f[i] = max(f[i], f[j] + 1);
}
}
ret = max(ret, f[i]);
}
cout << ret << endl;
return 0;
}3.神奇的幻方
题目: P2615 [NOIP 2015 提高组] 神奇的幻方

解法:模拟
这道题根据题意进行模拟即可,注意用x , y统计出上一个点的坐标。
这道题用else if,不然如果用多个if单独判断,有的k会同时满足多个条件。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 50;
int a[N][N];
int n;
int x, y; //统计前一个数的横纵坐标
int main()
{
cin >> n;
a[1][(n + 1) / 2] = 1;
x = 1, y = (n + 1) / 2;
for(int k = 2; k <= n * n; k++)
{
if(x == 1 && y == n) //条件 3
{
a[x + 1][y] = k;
x++;
}
else if(x == 1) //条件 1
{
a[n][y + 1] = k;
x = n; y++;
}
else if(y == n) //条件 2
{
a[x - 1][1] = k;
x--; y = 1;
}
else //条件 4
{
if(a[x - 1][y + 1] == 0)
{
a[x - 1][y + 1] = k;
x--; y++;
}
else
{
a[x + 1][y] = k;
x++;
}
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
return 0;
}4.挖地雷

解法:动态规划--最长上升子序列求方案
这里是新的题型,求具体的方案。针对这里类的问题会在最短路问题/背包问题/路径类问题/dp 中要求输出具体的方案是什么。
我们可以用pre[i]数组来记录当前结点的前驱结点是谁,然后最后通过dfs递归(从尾到头)回溯输出(从头到尾)。
这道题也可以转化为在一个路径(区间)中找和最大的方案,且要求前面的点能走到后面的点,根据题目给的图结构可得,对于i 号位置,只能从前面的某一个位置转移过来。因此,原问题就变成:在1 ~ n 中挑出一个可行的序列,这个序列中地雷的总数是最大的。就变成了一个最长上升子序列问题。用图存储可以是一个有向图。 当然也可以用dfs/拓扑排序 + 动态规划。
pre[i]表示:从pre[i]走到i位置的时候的最优解。
1.状态表式:f[i]表示走到i位置的时候,此时能挖到的最大地雷数。
2.状态转移方程:划分情况:1.本身初始为cnt[i]; 2.如果j->i(edges[j] [i] == 1), 且f[i] < f[j] + cnt[i],更新f[i] = f[j] + cnt[i], pre[i] = j。
3.初始化:不用。
4.填表顺序:从左到右。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 25;
int n;
int cnt[N];
int edges[N][N];
int f[N], pre[N];
void dfs(int x)
{
if(pre[x]) dfs(pre[x]);
cout << x << " ";
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
cin >> cnt[i];
for(int i = 1; i < n; i++)
{
for(int j = i + 1; j <= n; j++)
{
cin >> edges[i][j];
}
}
for(int i = 1; i <= n; i++)
{
f[i] = cnt[i];
for(int j = 1; j < i; j++)
{
if(edges[j][i] && f[j] + cnt[i] > f[i])
{
f[i] = f[j] + cnt[i];
pre[i] = j;
}
}
}
int ret = 0, pos = 0;
for(int i = 1; i <= n; i++)
{
if(f[i] > ret)
{
ret = f[i];
pos = i;
}
}
dfs(pos);
cout << endl << ret << endl;
return 0;
}5.路标设置

题目: P3853 [TJOI2007] 路标设置
解法:二分答案
这里"空旷指数"(最大距离)最小,可以想到二分。
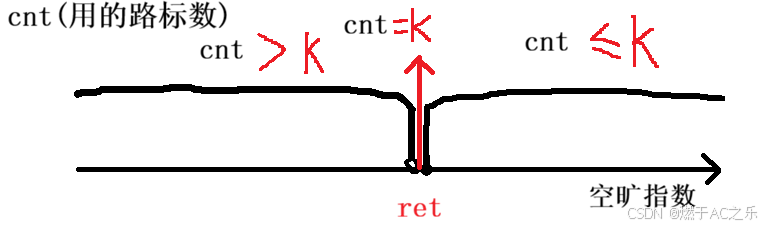
1.去寻找二段性:
二段性:设最优解为ret:
如果x >= ret ,需要设置路标的数量就小于等于k;
如果x < ret ,需要设置路标的数量就大于k。
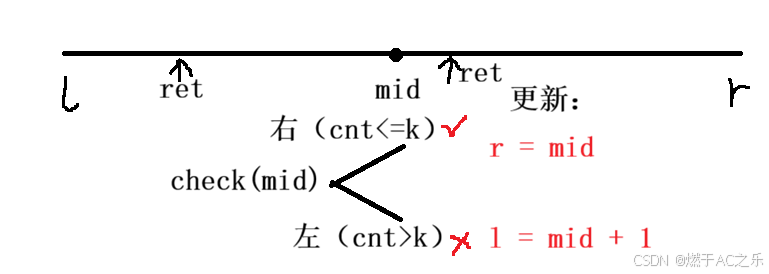
2.check函数:
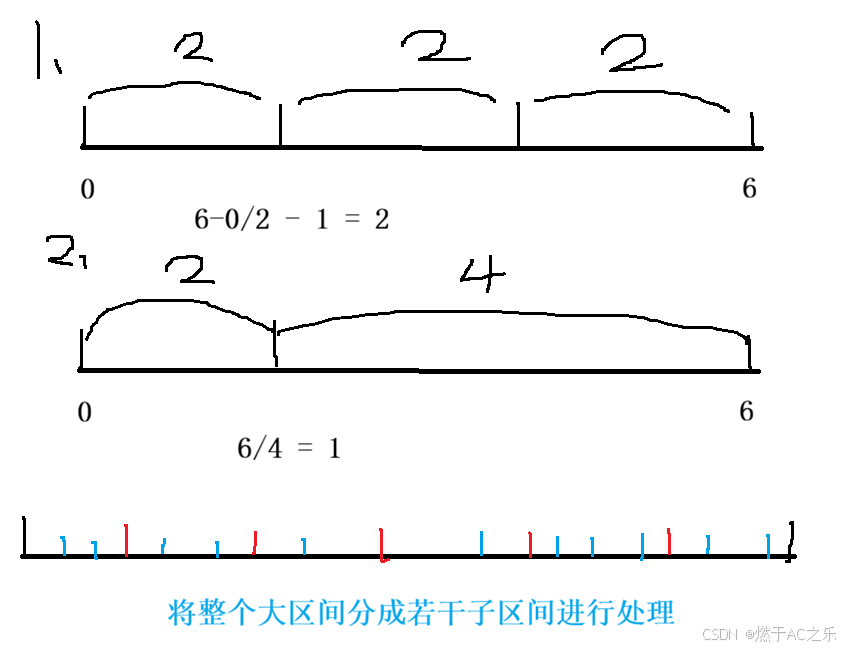
对于一个数x ,如何判断设置路标的数量:
设d = a [i ] - a [i - 1 ],那么需要路标的数量就是d / x;
如果d % x == 0 ,此时就可以少用一个路标 。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int len, n, k;
int a[N];
bool check(int x)
{
int cnt = 0;
for(int i = 2; i <= n; i++) //多段区间
{
int d = a[i] - a[i - 1];
cnt += d / x;
if(d % x == 0) cnt--; //刚好划分
}
return cnt <= k;
}
int main()
{
cin >> len >> n >> k;
for(int i = 1; i <= n; i++) cin >> a[i];
int l = 1, r = len;
while(l < r)
{
int mid = (l + r) / 2;
if(check(mid)) r = mid;
else l = mid + 1;
}
cout << l << endl;
return 0;
}6.关押罪犯
题目: P1525 [NOIP 2010 提高组] 关押罪犯
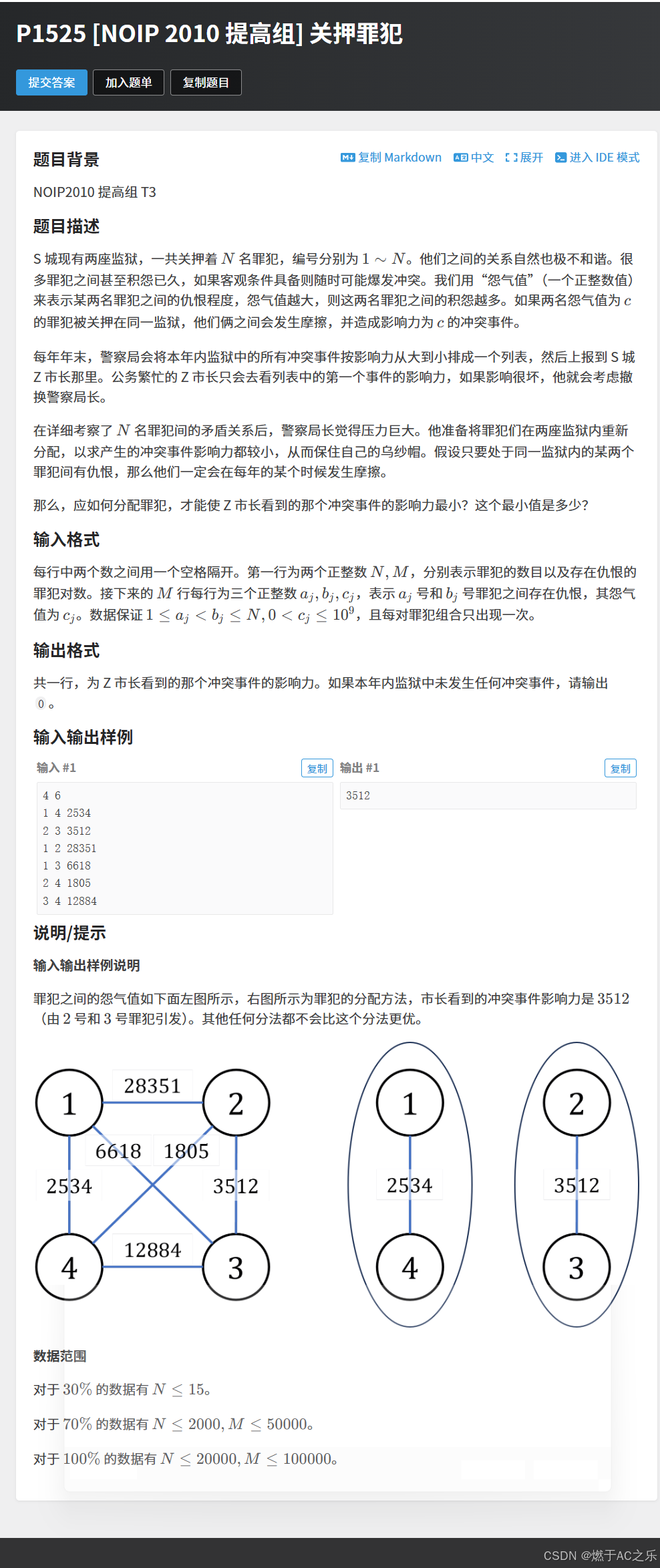
解法:贪心 + 扩展域并查集
这道题看到要使最大影响力最小,想到二分算法,但是check函数不好写,要用二分图匹配。
这道题还有更有解。
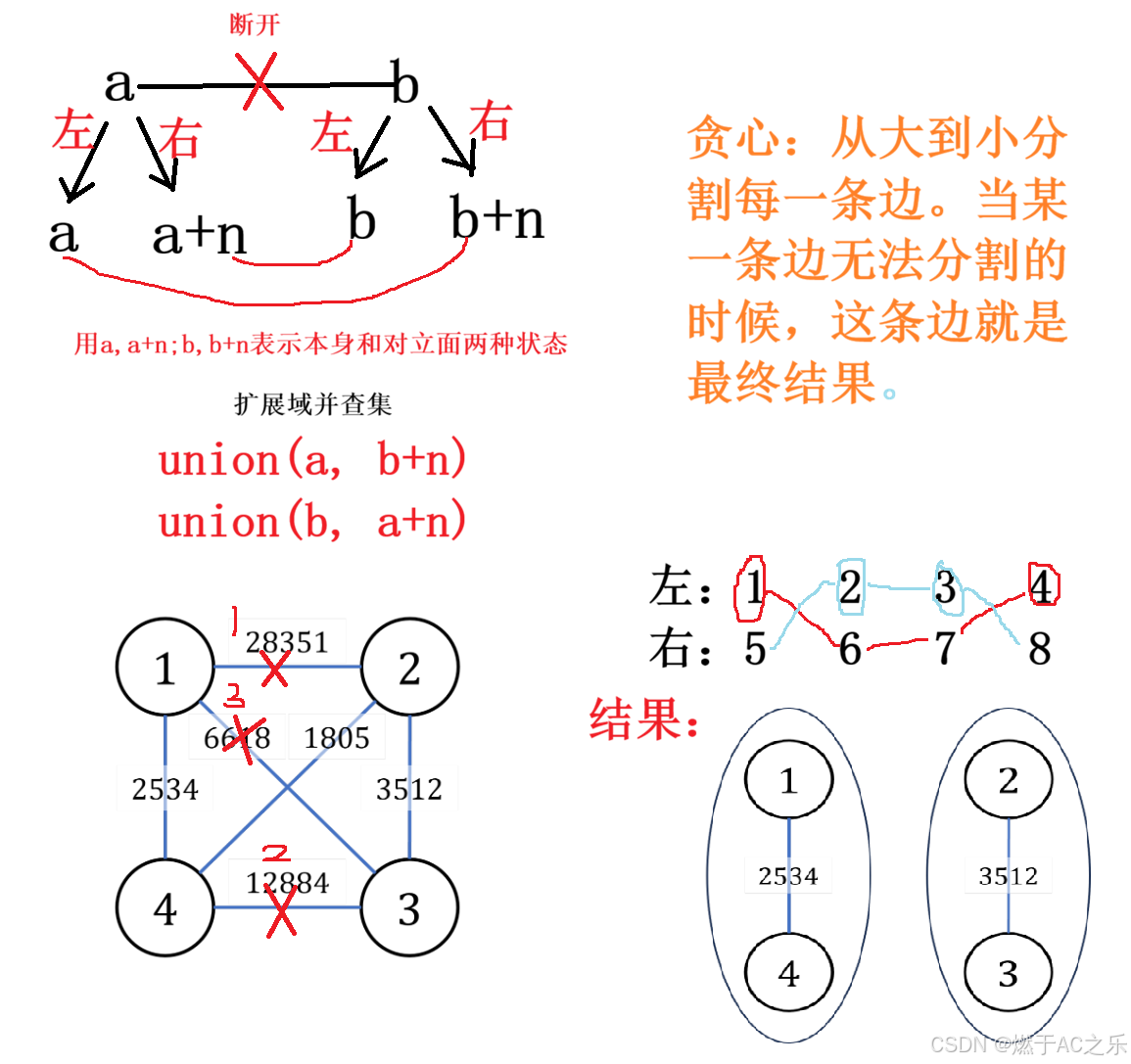
贪心:从大到小分割每一条边。当某一条边无法分割的时候,这条边就是最终结果。
可以利用扩展域并查集维护每一条边断开后的两个集合,并且判断某条边是否能够断开:
先断开:合并a 和b +n,b 和a +n;
判断是否能断开:判断a 和b 是否在同一个集合中 。
代码:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 4e4 + 10, M = 1e5 + 10; //N二倍
int n, m;
struct node
{
int a, b, c;
}e[M];
int fa[N];
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void un(int x, int y)
{
fa[find(x)] = find(y);
}
bool cmp(node& x, node& y)
{
return x. c > y.c;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
cin >> e[i].a >> e[i].b >> e[i].c;
//初始化
for(int i = 1; i <= n + n; i++)
fa[i] = i;
sort(e + 1, e + 1 + m, cmp);
for(int i = 1; i <= m; i++)
{
int a = e[i].a, b = e[i].b, c = e[i].c;
un(a, b + n);
un(b, a + n);
if(find(a) == find(b))
{
cout << c << endl;
return 0;
}
}
//全部断开,边界情况细节
cout << 0 << endl;
return 0;
}


加油!志同道合的人会看到同一片风景。
看到这里请点个赞 ,关注 ,如果觉得有用就收藏 一下吧。后续还会持续更新的。 创作不易,还请多多支持!