直流无刷电机FOC控制算法

文章目录

1、FOC概述
- [1.1 FOC控制算法介绍](#1.1 FOC控制算法介绍)
2、无刷电机
- [2.1 无刷电机介绍](#2.1 无刷电机介绍)
- [2.2 无刷电机和永磁同步电机的区别](#2.2 无刷电机和永磁同步电机的区别)
- [2.3 无刷电机的控制原理](#2.3 无刷电机的控制原理)
- - [2.3.1 无刷电机工作原理](#2.3.1 无刷电机工作原理)
  - [2.3.2 直流无刷电机驱动原理](#2.3.2 直流无刷电机驱动原理)
  - - [2.3.2.1 有感直流无刷电机六步换相驱动原理](#2.3.2.1 有感直流无刷电机六步换相驱动原理)
    - [2.3.2.2 直流无刷电机FOC控制原理](#2.3.2.2 直流无刷电机FOC控制原理)
3、无刷电机FOC控制算法
- [3.1 FOC控制算法整体流程](#3.1 FOC控制算法整体流程)
- [3.2 FOC算法Clarke变换](#3.2 FOC算法Clarke变换)
- - [3.2.1 Clarke变换公式推导](#3.2.1 Clarke变换公式推导)
  - [3.2.2 Clarke逆变换公式推导](#3.2.2 Clarke逆变换公式推导)
- [3.3 FOC算法Park变换](#3.3 FOC算法Park变换)
- - [3.3.1 Park变换公式推导](#3.3.1 Park变换公式推导)
  - [3.3.2 Park逆变换公式推导](#3.3.2 Park逆变换公式推导)
- [3.4 FOC算法SVPWM（空间矢量脉冲调制）原理及实现](#3.4 FOC算法SVPWM（空间矢量脉冲调制）原理及实现)
- - [3.4.1 SVPWM原理及实现](#3.4.1 SVPWM原理及实现)
  - [3.4.2 七段式SVPWM和五段式SVPWM的区别](#3.4.2 七段式SVPWM和五段式SVPWM的区别)
  - [3.4.3 基本矢量电压](#3.4.3 基本矢量电压)
  - [3.4.4 扇区判断](#3.4.4 扇区判断)
  - [3.4.5 相邻两个基本矢量电压的作用时间](#3.4.5 相邻两个基本矢量电压的作用时间)
  - [3.4.6 根据时间计算三路PWM占空比](#3.4.6 根据时间计算三路PWM占空比)
- [3.5 FOC矢量控制C语言代码](#3.5 FOC矢量控制C语言代码)
- - [3.5.1 FOC矢量控制foc.c文件代码](#3.5.1 FOC矢量控制foc.c文件代码)
  - [3.5.1 FOC矢量控制foc.h文件代码](#3.5.1 FOC矢量控制foc.h文件代码)
4、STM32CUBEMX配置
5、代码讲解

1、FOC概述

1.1 FOC控制算法介绍

FOC(Field-Oriented Control) ：直译是磁场定向控制，也被称作矢量控制 ，是目前无刷直流电机(BLDC)和永磁同步电机(PMSM)高效控制的最优方法之一，FOC算法指的是在通过精确地控制磁场大小与方向，使得电机的运动转矩平稳、噪声小、效率高，并且具有高速的动态响应无刷电机。

2、无刷电机

2.1 无刷电机介绍

无刷电机 （Brushless Motor ）是一种电动机，与传统的有刷电机相比，无刷电机没有刷子和换向器，因此具有更高的效率和可靠性。无刷电机采用电子换向技术，通过电子控制器来实现换向，从而使电机能够自动调整转子磁场与定子磁场之间的相对位置，实现转子的旋转。

无刷电机 由定子和转子组成。定子上有若干个线圈，通过电流激励产生磁场。转子上有永磁体或者通过电流激励产生磁场。当电流通过定子线圈时，定子线圈产生的磁场与转子磁场相互作用，使得转子受到力矩作用而旋转。
无刷电机具有以下优点：

1.高效率 ：无刷电机没有摩擦损耗和电刷损耗，因此具有更高的效率。

2.高功率密度 ：无刷电机体积小、重量轻，功率密度高。

3.高速度范围 ：无刷电机转速范围广，可以实现高速运转。

4.高可靠性 ：无刷电机没有电刷和换向器，减少了故障点，提高了可靠性。

5.低噪音：无刷电机运行平稳，噪音低。

2.2 无刷电机和永磁同步电机的区别

无刷直流电机 (BLDC)和永磁同步电机 (PMSM)比较相似，两者的主要区别是反电动势的波形.，无刷直流电机 (BLDC)反电动势接近于梯形波, 而 永磁同步电机 (PMSM) 反电动势接近于正弦波;

下图是无刷直流电机和永磁同步电机反电动势波形图 ：

2.3 无刷电机的控制原理

2.3.1 无刷电机工作原理

首先我们回忆下高中知识------安培定则，也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。我们这里利用定则之一：当用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的 N 极。如下图所示：

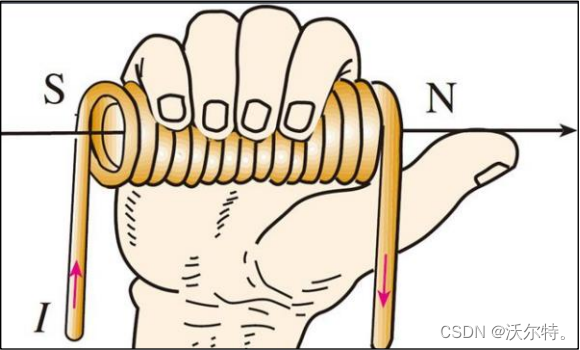
根据通电线圈会产生磁场，我们可以把通电线圈的磁场看成一个磁体，如下图：

磁体之间，存在异性相吸，同性相斥的原理，通电线圈和永磁体之间同样存在，而无刷电机就是利用了通电线圈和永磁体的相互作用原理，下面看下 BLDC(内置转子式无刷电机) 的内部结构图：

无刷电机有 3 根电机线按顺序依次叫 U 相线(一般为黄色)，V 相线(一般为绿色)和 W 相线(一般为蓝色)，3 组漆包线绕组的一端连接在一起，另外一端引出即为 UVW 相线，所以任意两根相线通电都可以导通这两个线圈;

2.3.2 直流无刷电机驱动原理

2.3.2.1 有感直流无刷电机六步换相驱动原理

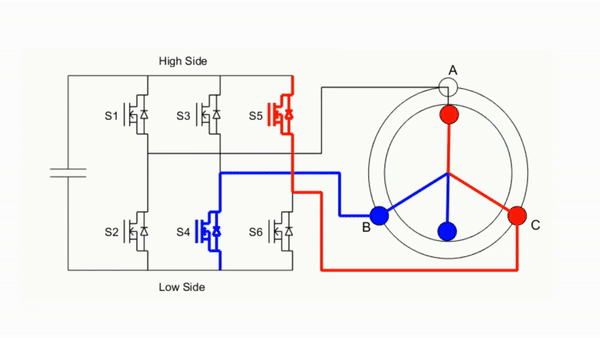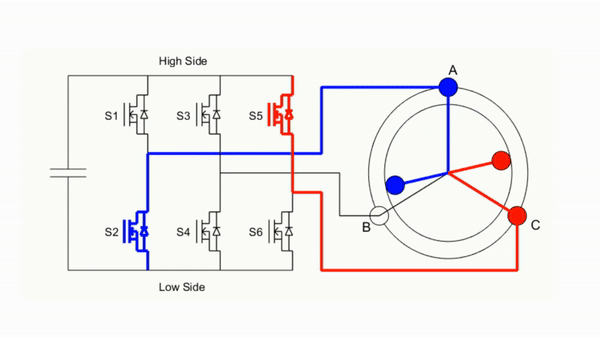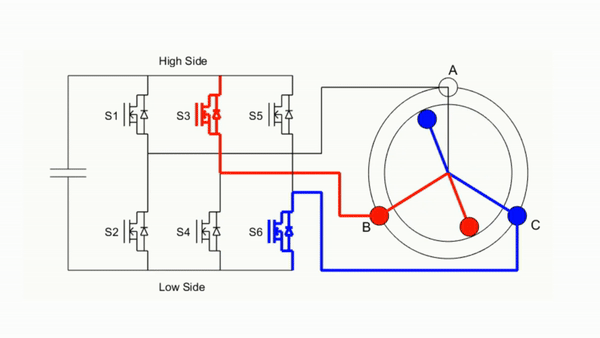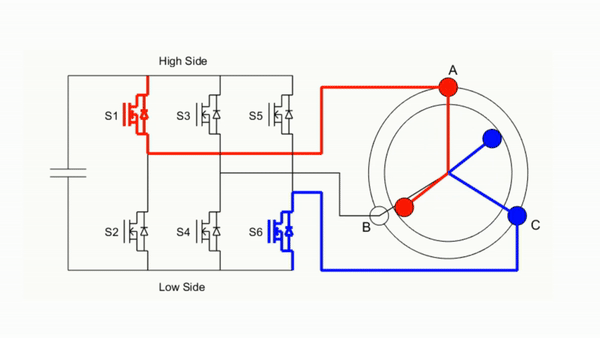
直流无刷电机驱动电路由三个半桥控制电路组成，通过控制三个半桥的上下桥导通和关断，实现逆变控制，将直流电变成交流电，简单点理解就是可以实现流过电机三相线圈的电流的流向控制，是通过使用三相你变电路来实现驱动电机，如下图所示；

所谓的三相逆变电路就是由三个半桥构成的电路，如上图中的 A+与 A-为一个半桥，B+与 B-以及 C+与 C-各自又为一个半桥，共三个半桥；这三个半桥各自控制对应的 A、B、C 三相绕组；当控制 A 的上桥臂 A+导通时，此时 A 相绕组接到电源正，当控制 B 的下桥臂B-导通时，此时 B 相绕组接到电源负，所以此时电流由 A 流向 B。

由于有感直流无刷电机的运行方式为绕组两两导通，所以三相线圈的导通组合只有 6 种通电情况，根据合理的顺序依次切换通电顺序即可让转子跟着磁场转起来。如下图是六步换相导通的情况：

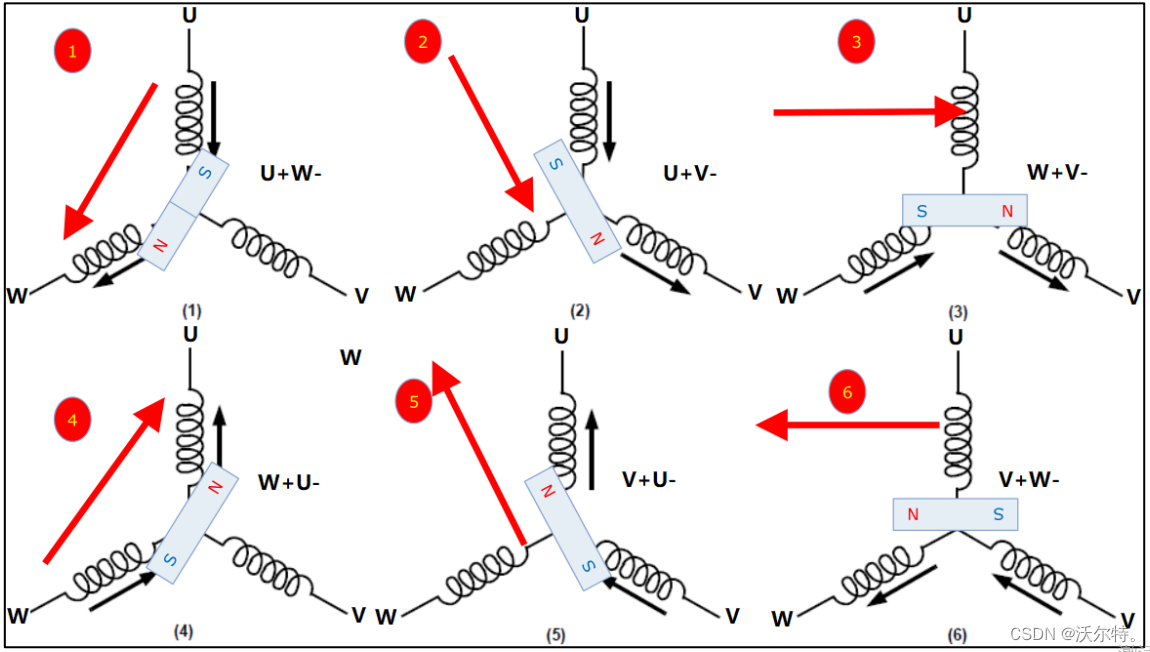
想要控制无刷电机绕组的极性，只需要控制绕组对应半桥的"上桥臂导通"或者"下桥臂导通"就可以实现控制该相连接至"正极"或者"负极"了，但是要注意不可以同侧半桥上下桥臂同时导通，负责会短路，烧毁电机！要实现6 步换相控制无刷电机转起来，就可以通过三相逆变电路来实现，如下图；

无刷电机依靠传感器提供转子位置信息进行驱动的方式我们称之为有感驱动方式，直流无刷电机六步换相控制需要通过霍尔传感器判断电机转子的位置，无刷电机的传感器一般为霍尔传感器，根据霍尔器件可检测磁场的变化的特性再搭配一定的电路将磁场方向变化信号转化成不同的高低电平信号输出；

霍尔传感器安装的以 120°电角度所安装，如下图所示；

下图为电机旋转时三个霍尔传感器输出的波形，所对应的扇区组合。通过三个霍尔传感器输出的波形就可以判断当前转子的具体位置，同样满足 6 步一周期。

六步换向需要依赖霍尔传感器反馈的转子位置，其相对应的就是三相逆变电路的上下桥臂导通情况，如下表所示。

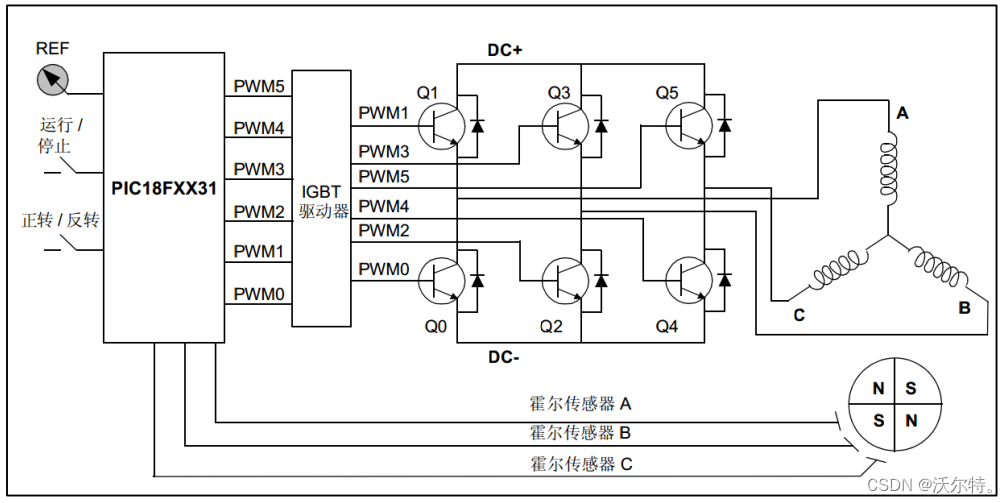
下图为直流无刷电机六步换相控制动态图；

下图为有感驱动无刷电机整体框图；

2.3.2.2 直流无刷电机FOC控制原理

我们从原理上简单的讲解了下FOC和六步换向的区别，而在实际控制中，FOC与六步换相还存在以下差别：

（1）控制信号区别：FOC采用正弦波驱动，六步换相采用方波驱动；

（2）控制方式区别：FOC控制中三个半桥的MOS采用三三导通，而六步换相采用两两导通

3、无刷电机FOC控制算法

3.1 FOC控制算法整体流程

下面是FOC控制算法的流程图：

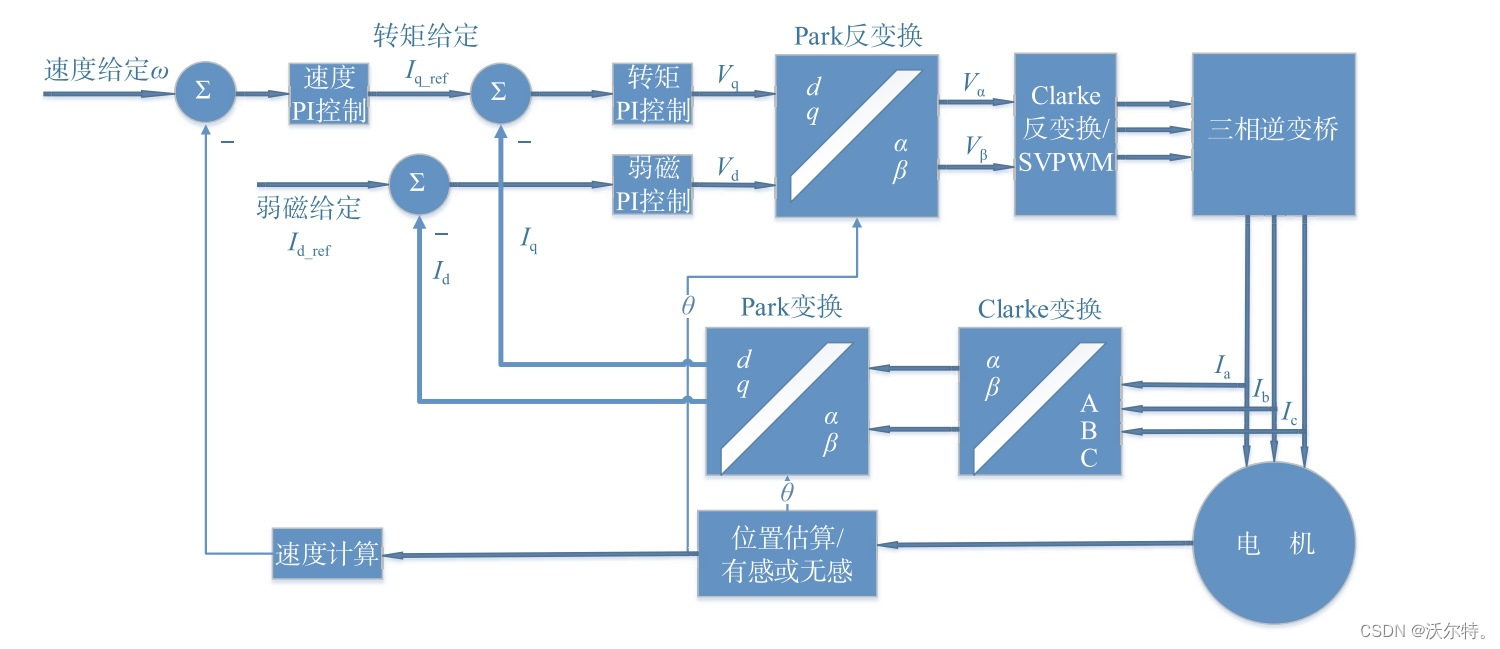
FOC控制算法的实现流程，主要氛围以下几大步：

（1）采集电机三相相电流 Ia Ib Ic

（2）将三相相电流通过 Clark 变化得到 Iα Iβ

（3）将 Iα Iβ 通过 Park 变化得到 Id Iq

（4）根据 Id Iq 和目标 Id_target Iq_target 进行 PID 计算得到 Uq Ud (电流环)

（5）将 Uq Ud 通过反 Park 变换得到 Uα Uβ

（6）将 Uα Uβ 作为SVPWM的输入，得到三路半桥的PWM输出定时器的比较寄存器值CCR

3.2 FOC算法Clarke变换

clark变化也就是将无刷电机静止的三相相电流 Ia Ib Ic三相坐标系转化为静止的 α-β 两相直角坐标系。

下图为三相相电流 Ia Ib Ic三相坐标系的动态图 ：

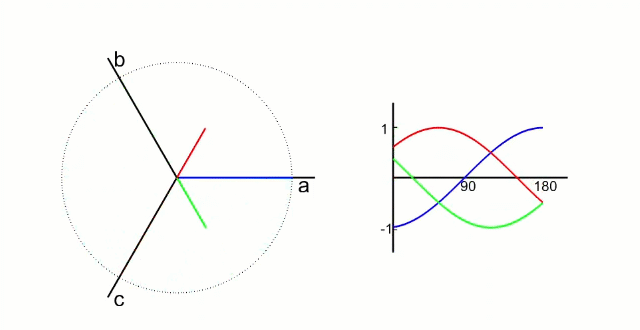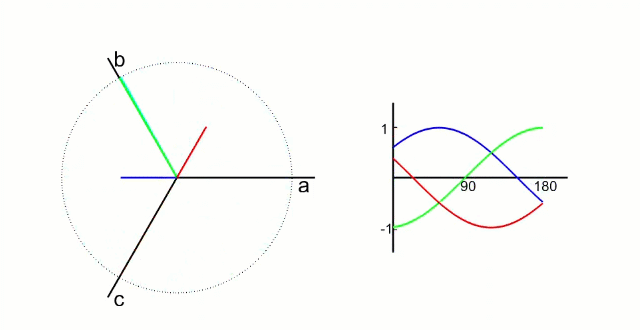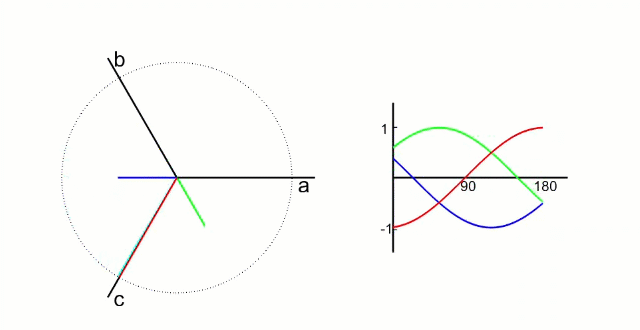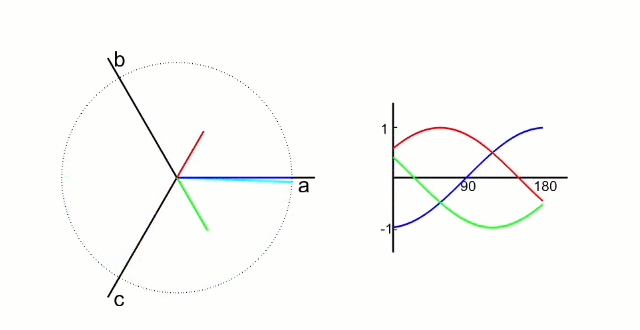
下图为转换成α-β 两相直角坐标系的动态图 ：

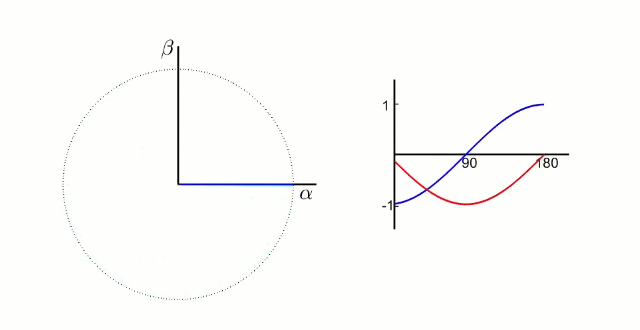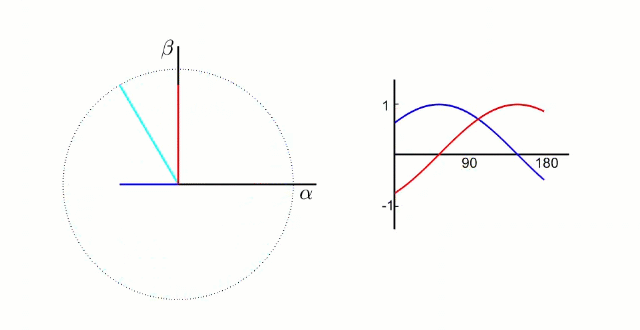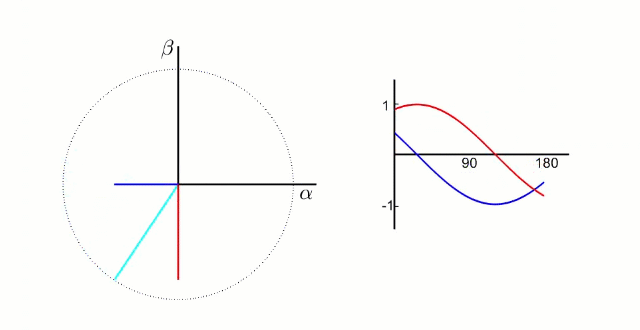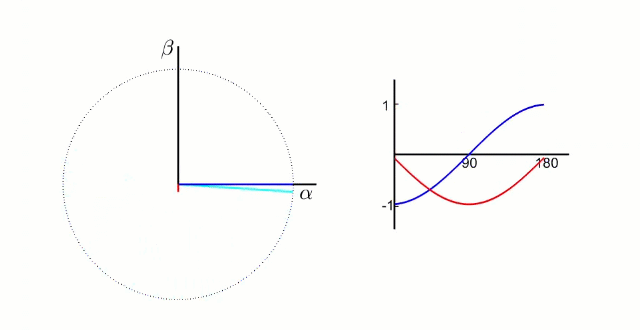
3.2.1 Clarke变换公式推导

通过ADC采样得到电机的Ia和Ib两项电流信息，由于基尔霍夫电流定律 (公式：Ia + Ib + Ic = 0)，同一个节点流入电流值与流出电流相等，我们可以计算出Ic，三个电流的相位差为120°，如下图所示；

通过Clark变换，将三相定子坐标系（三个轴互为120°，Ia , Ib , Ic）转化为两相的定子直角坐标系（i α , i β）这个过程有点类似于力的矢量分解，把三相映射到两相的坐标轴之上，如下图所示。

根据上图把三相映射到两相的坐标轴之上，可以得出Clarke变换的推导公式为：

将上式写成矩阵形式：

上式中，系数K = 2/3，变换前后，幅值不变,（既合成矢量的大小和方向相等），等幅值变换其实就是将Iα =Ia，将系数K = 2/3代入上式得 ：

再根据基尔霍夫电流定律Ia + Ib + Ic = 0得出等幅值Clarke变换的最终结果为：

3.2.2 Clarke逆变换公式推导

我们学习了怎么把一个三相时域上的复杂问题用矢量表示，并且用克拉克变换对它进行了降维，得到了降维后的简化表达形式。那么，有没有什么办法能够反过来把降维后的形式重新升维变回原来的Ia,Ib,Ic三相电流波形呢？有，这就被称为克拉克逆变换。这个在后续的FOC算法中也会很常用到。趁热打铁，我们来看一看怎么进行克拉克逆变换。

我们已经知道了克拉克变换后的Iα 、Iβ，我们在此基础上研究Clarke逆变换，首先，Ia的逆变换我们是不需要研究的，因为我们已经知道了Iα =Ia。

进一步的，我们研究逆变换Ib:

最后，还是根据基尔霍夫电流定律 ：Ia + Ib + Ic = 0,我们得到逆变换Ic：

则克拉克逆变换三式皆得，总结如下：

3.3 FOC算法Park变换

将电机三相相电流通过 Clark 变化得到 Iα Iβ，然后再将Iα Iβ通过变换得到随电机转子转动的Iq Id坐标系称为Park变换。

3.3.1 Park变换公式推导

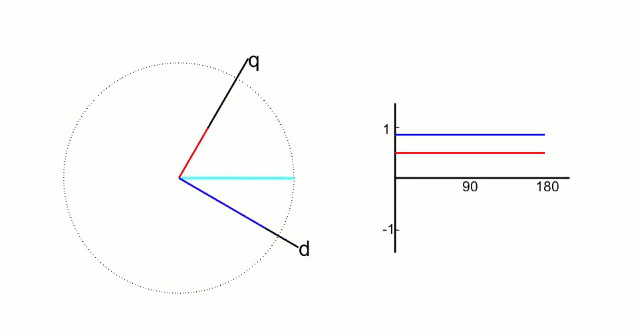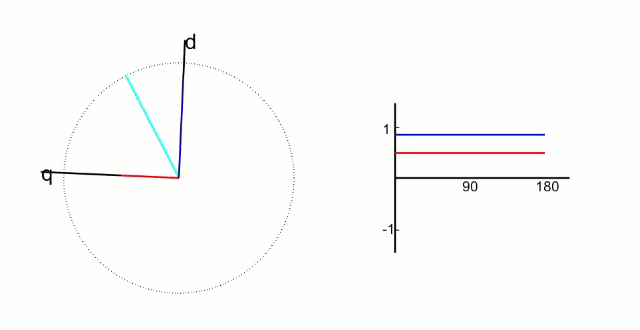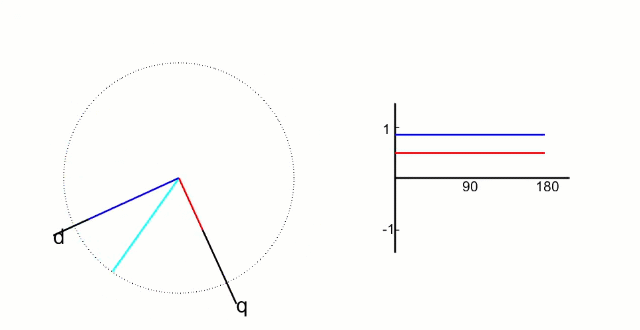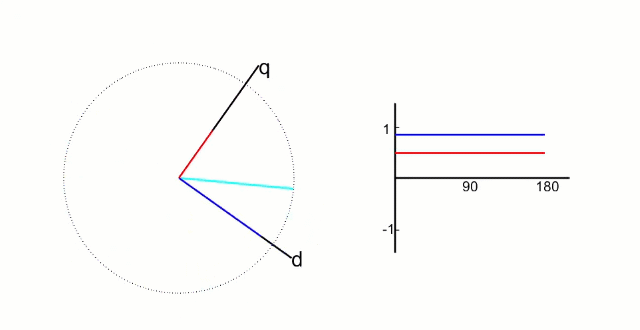
根据上图，角度θ是d轴与两相静止坐标系α轴的夹角。根据三角关系推出，Iα在d轴上的投影分量为Iαcosθ，q轴与β轴的夹角为θ2，可以得出θ2 = θ，因此iβ在d轴上的投影分量为iβsinθ; iα在q轴上的投影分量为-iαsinθ，因为它的投影分量在q轴的负方向上; iβ在q轴上的投影分量为iβscosθ。综合以上，可以得出公式:

这个id,iq坐标系是始终跟着转子旋转的；

（1）d 轴方向与转子磁链方向重合，又叫直轴；

（2）q 轴方向与转子磁链方向垂直，又叫交轴；

经过这一步的变换，我们会发现，一个匀速旋转向量在这个坐标系下变成了一个定值，这个坐标系下两个控制变量都被线性化了，如下图所示；

3.3.2 Park逆变换公式推导

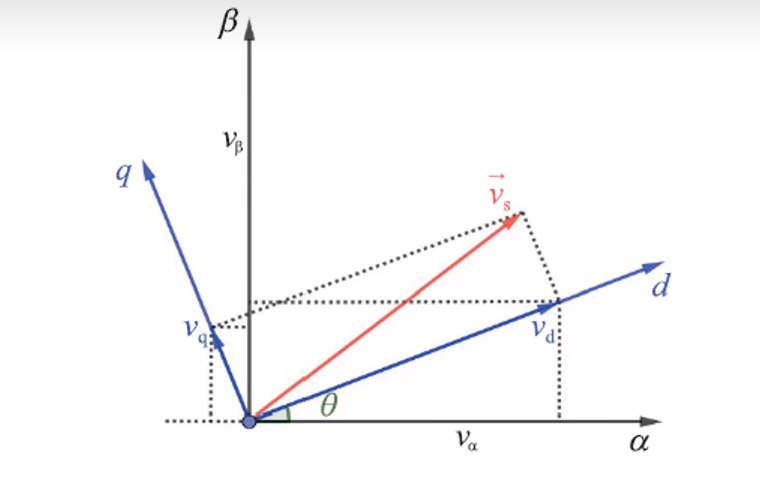
Vd在β轴上的投影分量为Vdsinθ，Vq在β轴上的投影分量为Vqcosθ，由此可得出下式：

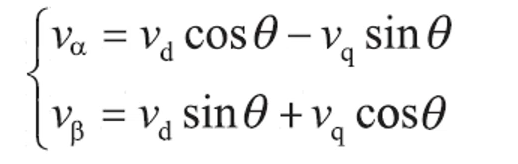
3.4 FOC算法SVPWM（空间矢量脉冲调制）原理及实现

3.4.1 SVPWM原理及实现

SVPWM （Space Vector Pulse Width Modulation ）即空间矢量脉宽调制。它通过三项你变器的6个功率管输出随时间变化的PWM波，模拟三项对称正弦波电流形成的电压矢量园，产生接近圆形的磁链轨迹。SVPWM的原理如下：

（1）基本矢量电压 ：SVPWM将三相电压分解为两个正弦波和一个直流分量，这三个分量构成了基本矢量电压。

（2）扇区判断 ：根据电机的电角度，判断当前所处的扇区。扇区是将电机的360度分为六个等分，每个扇区对应一个基本矢量电压。

（3）计算相邻两个基本矢量电压的作用时间 ：根据当前所处的扇区，计算相邻两个基本矢量电压的作用时间。作用时间是指每个基本矢量电压在一个电周期内的持续时间。

（4）三路PWM占空比计算 ：根据相邻两个基本矢量电压的作用时间，计算三相PWM的占空比。占空比是指PWM信号高电平的持续时间与一个电周期的比值。
算法流程如下：
step1 ：根据电机的电角度，判断当前所处的扇区。
step2 ：根据当前所处的扇区，计算相邻两个基本矢量电压的作用时间。
step3：根据相邻两个基本矢量电压的作用时间，计算三相PWM的占空比。

3.4.2 七段式SVPWM和五段式SVPWM的区别

七段式SVPWM（Space Vector Pulse Width Modulation）和五段式SVPWM都是一种常用的交流电机控制方法，它们的主要区别在于矢量分解时所使用的向量数不同。

(1)七段式 ：七段式SVPWM使用七个不同的向量进行矢量分解，可以得到更高的电机效率和更低的谐波失真率。但是，七段式SVPWM需要更复杂的计算，因此需要更高的控制精度和计算能力。

(2)五段式 ：五段式SVPWM只使用五个向量进行矢量分解，计算较为简单，适用于控制较为简单的电机系统。但是，五段式SVPWM相对于七段式SVPWM的效率和失真率会略差一些。

本设计采用七段式SVPWM设计；

七段式SVPWM波形图

3.4.3 基本矢量电压

3.4.4 扇区判断

3.4.5 相邻两个基本矢量电压的作用时间

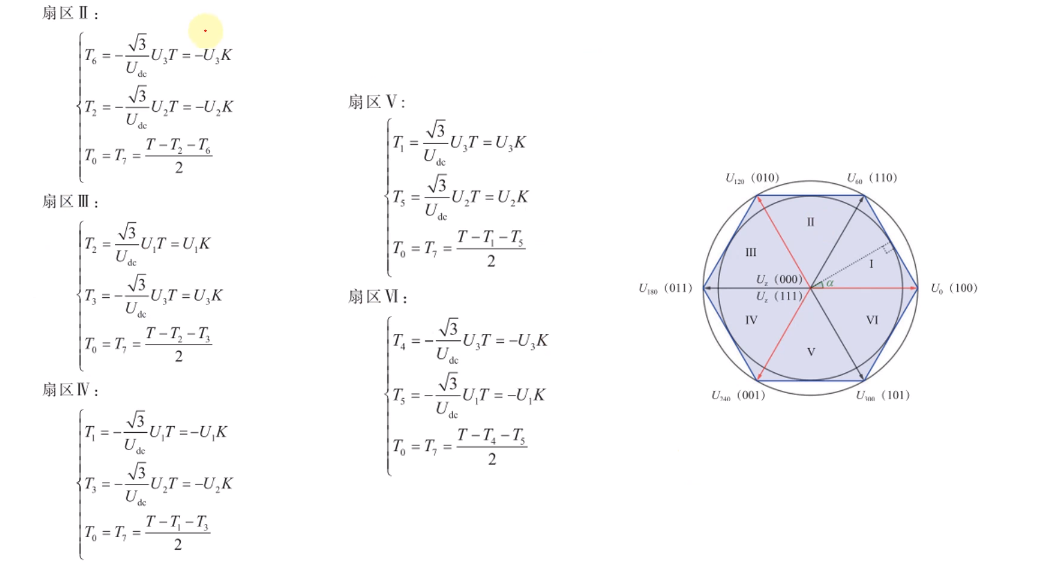
3.4.6 根据时间计算三路PWM占空比

根据上图(以扇区一为例)可以得出三路PWM占空比值的公式：

value_a = (tpwm - Ta - Tb)/4;

value_b = value_a + Ta/2;

value_c = value_b + Tb/2;

value_a：占空比占比最多；

value_b：占空比占比中等；

value_c：占空比占比最少；

每个扇区A、B、C占空比占比都不一样，根据3.4.2六个扇区的七段式波形图，得出的value_a、value_b、value_c代入相对应的扇区；

3.5 FOC矢量控制C语言代码

3.5.1 FOC矢量控制foc.c文件代码

c 复制代码

#include "foc.h"
//反Park变换，将静止两相坐标系D/Q转换为旋转两相坐标系Valpha/Vbeta
 void RevParkOperate(float vd,float vq,float theta,float *valpha,float *vbeta)
{
	*valpha = vd * cos(theta) - vq * sin(theta);
	*vbeta = vd * sin(theta) + vq * cos(theta);
}


//扇区判断函数，通过valpha和vbeta判断扇区
//返回值：315462对应扇区123456
unsigned char SectorJude(float valpha,float vbeta)
{
	float A = vbeta;
	float B = valpha  * sqrt3/2.0f - vbeta/2.0f;
	float C = -valpha * sqrt3/2.0f - vbeta/2.0f;
	unsigned char N = 0;
	
	if(A > 0)
	{
		N = N+1;
	}
	if(B > 0)
	{
		N = N+2;
	}
	if(C > 0)
	{
		N = N+4;
	}
	return N;
	
	
//	float U1 = vbeta;
//	float U2 = valpha  * sqrt3/2.0f - vbeta/2.0f;
//	float U3 = -valpha * sqrt3/2.0f - vbeta/2.0f;
//	unsigned char A = 0,B = 0,C = 0,N = 0;
//	
//	A= (U1>0)? 1:0;
//	B= (U2>0)? 1:0;
//	C= (U3>0)? 1:0;
//	
//	N = A + 2*B + 4*C;
//	
//	return N;
}

//矢量作用时间计算
void VectorActionTime(uint8_t n,float valpha,float vbeta,uint32_t udc,uint32_t tpwm,float *ta,float *tb)
{
	float X = (sqrt3 * tpwm) / udc * vbeta;
	float Y = (sqrt3 * tpwm) / udc * ((sqrt3/2.0f)*valpha - vbeta/2.0f);
	float Z = (sqrt3 * tpwm) / udc * (-(sqrt3/2.0f)*valpha - vbeta/2.0f);
	
	if(n == 3) //第一扇区
	{
		*ta = Y;
		*tb = X;
	}
	if(n == 1) //第二扇区
	{
		*ta = -Y;
		*tb = -Z;
	}
	if(n == 5) //第三扇区
	{
		*ta = X;
		*tb = Z;
	}
	if(n == 4) //第四扇区
	{
		*ta = -X;
		*tb = -Y;
	}
	if(n == 6) //第五扇区
	{
		*ta = Z;
		*tb = Y;
	}
	if(n == 2) //第六扇区
	{
		*ta = -Z;
		*tb = -X;
	}
}

//CCR时间计算
void CCRCalculate(uint8_t n,float ta,float tb,uint32_t tpwm,uint32_t *ccr1,uint32_t *ccr2,uint32_t *ccr3)
{
	/*限制ta和tb，ta+tb不能超过tpwm*/
	float temp = ta + tb;
	if(temp > tpwm)
	{
		ta = ta / temp*tpwm;
		tb = tb / temp*tpwm;
	}
	
	float value1 = (tpwm - ta - tb)/4.0f;
	float value2 = value1 + ta/2.0f;
	float value3 = value2 + tb/2.0f;
	
	switch(n)
	{
		case 3:
			*ccr1 = value1;
		  *ccr2 = value2;
		  *ccr3 = value3;
		break;
		case 1:
			*ccr1 = value2;
		  *ccr2 = value1;
		  *ccr3 = value3;
		break;
		case 5:
			*ccr1 = value3;
		  *ccr2 = value1;
		  *ccr3 = value2;
		break;
		case 4:
			*ccr1 = value3;
		  *ccr2 = value2;
		  *ccr3 = value1;
		break;
		case 6:
			*ccr1 = value2;
		  *ccr2 = value3;
		  *ccr3 = value1;
		break;
		case 2:
			*ccr1 = value1;
		  *ccr2 = value3;
		  *ccr3 = value2;
		break;
	}
}


//通过Vd,Vq,THETA,Udc,Tpwm计算每一步的CCR值并写入定时器
/*
Vd:给电机Vd的电压
Vq:给电机Vq的电压
theta:电角度
theta:母线电压
tpwm:PWM周期
*/
void SvpwmAlgorithm(float vd,float vq,float theta,uint32_t udc,uint32_t tpwm)
{
	float valpha = 0;
	float vbeta = 0;
	RevParkOperate(vd,vq,theta,&valpha,&vbeta);//计算当前valpha和vbeta
	
	unsigned char n = SectorJude(valpha,vbeta);//计算当前扇区
	
	float ta = 0;
	float tb = 0;
	VectorActionTime(n,valpha,vbeta,udc,tpwm,&ta,&tb);//计算两个矢量的作用时间
	
	uint32_t ccr1 = 0;
	uint32_t ccr2 = 0;
	uint32_t ccr3 = 0;
	CCRCalculate(n,ta,tb,tpwm,&ccr1,&ccr2,&ccr3);//CCR时间计算（计算占空比值）
	
	 __HAL_TIM_SET_COMPARE(&htim8,TIM_CHANNEL_1,ccr1);//输出三路占空比
	 __HAL_TIM_SET_COMPARE(&htim8,TIM_CHANNEL_2,ccr2);
	 __HAL_TIM_SET_COMPARE(&htim8,TIM_CHANNEL_3,ccr3);
}

3.5.1 FOC矢量控制foc.h文件代码

c 复制代码

#ifndef __FOC_H__
#define __FOC_H__
#include "tim.h"
#include <math.h> 
#include <stdio.h>

#define sqrt3 1.7320508f
void SvpwmAlgorithm(float vd,float vq,float theta,uint32_t udc,uint32_t tpwm);

void Clark_Park(float Electronic_Angle);

float motor_ramp(float t_value,float acc_time);

#endif

4、STM32CUBEMX配置

4.1、时钟原配置

4.2、调试接口配置

4.3、时钟配置

4.4、高级定时器配置(用于FOC算法，产生PWM)

4.5、ADC配置(用于电机三相电流采样)

5、代码讲解

5.1、foc算法控制算法代码.c文件

c 复制代码

#include "foc.h"
#include "spi.h"
#include "adc.h"


FOC_CURRENT foc_current;

//反Park变换，将静止两相坐标系D/Q转换为旋转两相坐标系Valpha/Vbeta
 void RevParkOperate(float vd,float vq,float theta,float *valpha,float *vbeta)
{
	*valpha = vd * cos(theta) - vq * sin(theta);
	*vbeta = vd * sin(theta) + vq * cos(theta);
}


//扇区判断函数，通过valpha和vbeta判断扇区
//返回值：315462对应扇区123456
unsigned char SectorJude(float valpha,float vbeta)
{
	float A = vbeta;
	float B = valpha  * sqrt3/2.0f - vbeta/2.0f;
	float C = -valpha * sqrt3/2.0f - vbeta/2.0f;
	unsigned char N = 0;
	
	if(A > 0)
	{
		N = N+1;
	}
	if(B > 0)
	{
		N = N+2;
	}
	if(C > 0)
	{
		N = N+4;
	}
	return N;
	
	
//	float U1 = vbeta;
//	float U2 = valpha  * sqrt3/2.0f - vbeta/2.0f;
//	float U3 = -valpha * sqrt3/2.0f - vbeta/2.0f;
//	unsigned char A = 0,B = 0,C = 0,N = 0;
//	
//	A= (U1>0)? 1:0;
//	B= (U2>0)? 1:0;
//	C= (U3>0)? 1:0;
//	
//	N = A + 2*B + 4*C;
//	
//	return N;
}

//矢量作用时间计算
void VectorActionTime(uint8_t n,float valpha,float vbeta,uint32_t udc,uint32_t tpwm,float *ta,float *tb)
{
	float X = (sqrt3 * tpwm) / udc * vbeta;
	float Y = (sqrt3 * tpwm) / udc * ((sqrt3/2.0f)*valpha - vbeta/2.0f);
	float Z = (sqrt3 * tpwm) / udc * (-(sqrt3/2.0f)*valpha - vbeta/2.0f);
	
	if(n == 3) //第一扇区
	{
		*ta = Y;
		*tb = X;
	}
	if(n == 1) //第二扇区
	{
		*ta = -Y;
		*tb = -Z;
	}
	if(n == 5) //第三扇区
	{
		*ta = X;
		*tb = Z;
	}
	if(n == 4) //第四扇区
	{
		*ta = -X;
		*tb = -Y;
	}
	if(n == 6) //第五扇区
	{
		*ta = Z;
		*tb = Y;
	}
	if(n == 2) //第六扇区
	{
		*ta = -Z;
		*tb = -X;
	}
}

//CCR时间计算
void CCRCalculate(uint8_t n,float ta,float tb,uint32_t tpwm,uint32_t *ccr1,uint32_t *ccr2,uint32_t *ccr3)
{
	/*限制ta和tb，ta+tb不能超过tpwm*/
	float temp = ta + tb;
	if(temp > tpwm)
	{
		ta = ta / temp*tpwm;
		tb = tb / temp*tpwm;
	}
	
	float value1 = (tpwm - ta - tb)/4.0f;
	float value2 = value1 + ta/2.0f;
	float value3 = value2 + tb/2.0f;
	
	switch(n)
	{
		case 3:
			*ccr1 = value1;
		  *ccr2 = value2;
		  *ccr3 = value3;
		break;
		case 1:
			*ccr1 = value2;
		  *ccr2 = value1;
		  *ccr3 = value3;
		break;
		case 5:
			*ccr1 = value3;
		  *ccr2 = value1;
		  *ccr3 = value2;
		break;
		case 4:
			*ccr1 = value3;
		  *ccr2 = value2;
		  *ccr3 = value1;
		break;
		case 6:
			*ccr1 = value2;
		  *ccr2 = value3;
		  *ccr3 = value1;
		break;
		case 2:
			*ccr1 = value1;
		  *ccr2 = value3;
		  *ccr3 = value2;
		break;
	}
}


//通过Vd,Vq,THETA,Udc,Tpwm计算每一步的CCR值并写入定时器
void SvpwmAlgorithm(float vd,float vq,float theta,uint32_t udc,uint32_t tpwm)
{
	float valpha = 0;
	float vbeta = 0;
	RevParkOperate(vd,vq,theta,&valpha,&vbeta);//计算当前valpha和vbeta
	
	unsigned char n = SectorJude(valpha,vbeta);//计算当前扇区
	
	float ta = 0;
	float tb = 0;
	VectorActionTime(n,valpha,vbeta,udc,tpwm,&ta,&tb);//计算两个矢量的作用时间
	
	uint32_t ccr1 = 0;
	uint32_t ccr2 = 0;
	uint32_t ccr3 = 0;
	CCRCalculate(n,ta,tb,tpwm,&ccr1,&ccr2,&ccr3);//CCR时间计算（计算占空比值）
	
	 __HAL_TIM_SET_COMPARE(&htim8,TIM_CHANNEL_1,ccr1);//输出三路占空比
	 __HAL_TIM_SET_COMPARE(&htim8,TIM_CHANNEL_2,ccr2);
	 __HAL_TIM_SET_COMPARE(&htim8,TIM_CHANNEL_3,ccr3);
}

/*FOC-Park和Clark变换*/
/*
APhaseCurrent：电机A相电流
BPhaseCurrent：电机B相电流
Electronic_Angle：电角度
*Current：Park、Clark变换之后的电流值
*/
void Clark_Park(int APhaseCurrent,int BPhaseCurrent,float Electronic_Angle,FOC_CURRENT *Current)
{
	    //Clark变换
			I_alfa = APhaseCurrent;
			I_beta = 1/sqrt3 * (2*BPhaseCurrent + APhaseCurrent);
	
	    //Park变换
			foc_current.Id = I_alfa*cos(Electronic_Angle) + I_beta*sin(Electronic_Angle);
			foc_current.Iq = -(I_alfa * sin(Electronic_Angle)) + I_beta*cos(Electronic_Angle);
	
	    foc_current.Id = foc_current.Id/1600.0;
	    foc_current.Iq = foc_current.Iq/1600.0;
}

5.2、foc算法控制算法代码.h文件

c 复制代码

#ifndef __FOC_H__
#define __FOC_H__
#include "tim.h"
#include <math.h> 
#include <stdio.h>

#define sqrt3 1.7320508f

/*FOC变换之后的电流值*/
typedef struct {
	float Id;
	float Iq;
}FOC_CURRENT;

extern FOC_CURRENT foc_current;

void SvpwmAlgorithm(float vd,float vq,float theta,uint32_t udc,uint32_t tpwm);
void Clark_Park(int APhaseCurrent,int BPhaseCurrent,float Electronic_Angle,FOC_CURRENT *Current);

#endif

5.3、主要运行代码

c 复制代码

/*TIM3回调函数*/
void HAL_TIM_PeriodElapsedCallback(TIM_HandleTypeDef *htim)/*进入中断时间为1ms秒*/
{
	if(htim->Instance==TIM3)
	{
	 if(motor_state ==1)
		{		
		Get_Pos();//编码器多圈数据累加
		Encoder_TypeDef.angle = Get_Elec_Angle();//获取机械角度
			
		/*角度补偿
		 Encoder_TypeDef.angle：电机的机械角度
		 Encoder_TypeDef.angle_rad_offset：电机零位的编码器的值
		*/
		if(Encoder_TypeDef.angle>=Encoder_TypeDef.angle_rad_offset)
		{
			Encoder_TypeDef.angle = Encoder_TypeDef.angle - Encoder_TypeDef.angle_rad_offset;
		}
		else
		{
			Encoder_TypeDef.angle = 6.2831852f - Encoder_TypeDef.angle_rad_offset + Encoder_TypeDef.angle;
		}
		Encoder_TypeDef.electronic_angle = Encoder_TypeDef.angle*7;//将机械角度转换成电角度
		Encoder_TypeDef.electronic_angle = fmod(Encoder_TypeDef.electronic_angle,6.2831852f);//将电角度限制在0-6.2831852f之间
		
		/*位置环*/
   PID_Position_Out = PID_Function(&pid_position_TypeDef,target_location,encoder.rad_comulative);//PID输出
		/*速度计算*/
   vel_LPF = LPF_velocity(MT6701_GetVelocity());//速度计算以及低通滤波处理
		/*速度环*/
	 PID_Speed_Out = PID_Function(&pid_speed_TypeDef,PID_Position_Out,vel_LPF);//PID输出
		/*Clark_Park变换*/
	 Clark_Park(PhaseACurrent,PhaseBCurrent,Encoder_TypeDef.electronic_angle,&foc_current);
		/*电流环*/
		PID_Out_Value = PID_Function(&pid_current_Typedef,PID_Speed_Out,foc_current.Iq);//PID输出
		
	 SvpwmAlgorithm(0,PID_Out_Value,Encoder_TypeDef.electronic_angle,12,3600);//SVPWM算法	
		}
	}
}