【递归算法】快速幂解决 pow(x,n)

一、题目解析

题目很简单，要求x的n次幂。

要注意n的取值范围：n可能是负数，这时候我们要利用数学中 x⁻ⁿ = 1 / xⁿ 来转换；n可能是 -2³¹，若转换成正数则会超过 int 类型的最大取值 2³¹-1。

二、算法原理

2.1 解法一：循环

思路很简单，循环n次即可。

Java 复制代码

for (int i = 0; i < n; i ++)  x *= x;

时间复杂度：O（N）

但是，当n取值很大时，比如 n = 1000，程序的效率就会降低，甚至超时。

2.2 解法二：快速幂

快速幂可以采用两种方法来实现：

递归实现✅
循环实现

我们这里采用递归实现。

先看示例1：

要求 2¹⁰，我们可以通过 2⁵ * 2⁵ 来得到；
要求 2⁵，我们可以通过 2² * 2² * 2 来得到；
要求 2²，我们可以通过 2 * 2 来得到；
要求 2，我们可以通过 2⁰ (1) * 2 来得到；

即：

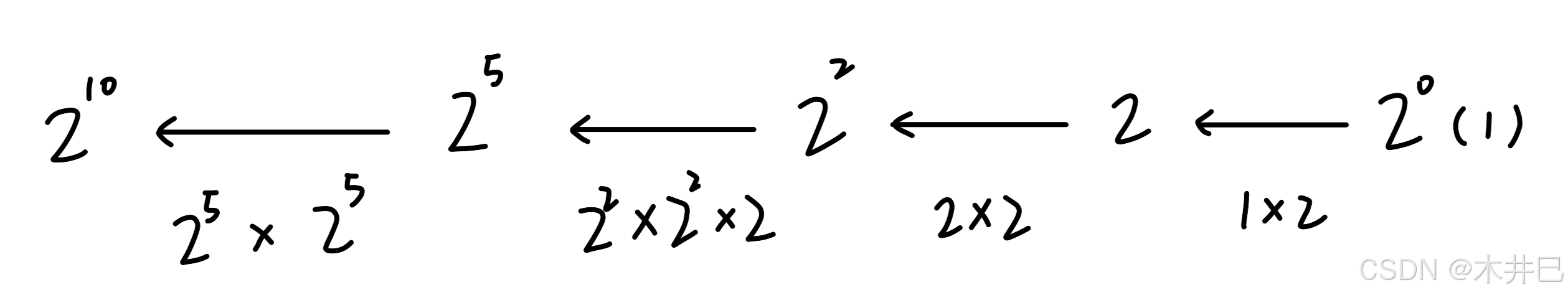
三、代码实现

设计函数头------寻找子问题：

根据算法原理，我们可以知道，该问题的子问题是：计算所给的x的n次幂

因此函数头有两个参数x、n，返回值为与所给的x相同的类型：double pow(double x, int n)

设计函数体------子问题所做的事：

每一个子问题都是先得到x的n / 2次幂，然后根据当前n的奇偶性决定是 xⁿ * xⁿ，还是 xⁿ * xⁿ * x，即：

temp = pow(x, n / 2)
return (n % 2 == 0) ? temp * temp ： temp * temp * temp

递归出口：

当 n == 0 时，返回1，因为所有数的0次幂都是1

代码实现如下：

Java 复制代码

class Solution {
    public double myPow(double x, int n) {
        // 分n为正负两个情况
        return (n < 0) ? 1.0 / pow(x, -n) : pow(x, n);
    }

	public double pow(double x, int n) {
		// 递归出口
		if (n == 0) return 1.0;
		
		double temp = pow(x, n / 2);
		// 分奇偶情况
		return (n % 2 == 0) ? temp * temp : temp * temp * x; 
	}
}