目录
[x 的平方根](#x 的平方根)
[LCR 173. 点名](#LCR 173. 点名)
朴素二分查找模版:(对应下面例题第一道)

查找区间左端点: (补充:x >= target 时,当前值可能是目标值的左边界,所以mid不能减 1 操作;其他细节在第二题中有解释)

查找区间右端点: (细节在第二题中有解释)

二分查找

**思路:**计算待查找区间的中间的数的下标,用这个值和目标值相比较,如果大于目标值,下次查找就在这个值左边的区间继续进行二分查找即可,如果小于目标值,下次就在这个值右边的区间继续进行二分查找,如果等于目标值,返回结果即可。
细节问题:
- **循环结束的条件:**left > right(left,right 分别指向待查找区间的最左边和最右边)
- **计算中间值防止溢出:**left + (right - left)/ 2
代码:
cpp
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2; //防止溢出
if (nums[mid] > target) right = mid - 1;
else if (nums[mid] < target) left = mid + 1;
else return mid;
}
return -1;
}
};在排序数组中查找元素的第一个和最后一个位置

**思路:**分别使用文章开头描述的找左右端点的方式找到目标值的起始和结束即可。
细节问题:
- 循环条件: left < right。当 left 等于 right,并且此时它们所指向的元素是目标值的时候,会造成死循环,所以循环条件中不能让 left 和 right 相等。
- 求中间点的操作:
-
找左边界: left + (right - left)/ 2。这里如果使用 left + (right - left + 1) / 2 可能会造成死循环,比如下图情况:使用 left + (right - left + 1) / 2 的方式算出的中间值是 right 所指向的元素,如果此时 right 指向的元素大于等于目标值,right 指针不会移动,下次计算中间值还是 right 指向的元素,这样就会造成一种死循环。
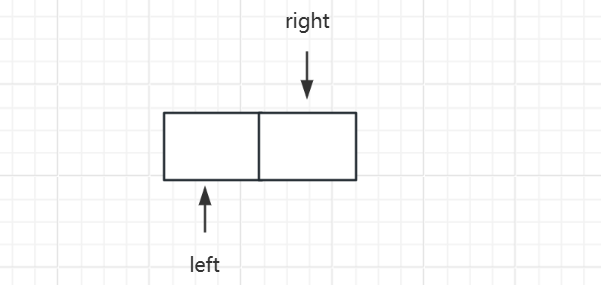
-
找右边界: left + (right - left + 1) / 2。和左边界同理,为了避免死循环。
-
代码:
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size() == 0)
return {-1, -1};
int left = 0;
int right = nums.size() - 1;
vector<int> ret;
while(left < right){
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
if(nums[left] == target) ret.push_back(left);
else return {-1, -1};
left = 0;
right = nums.size() - 1;
while(left < right){
int mid = left + (right - left + 1) / 2;
if(nums[mid] > target) right = mid - 1;
else left = mid;
}
ret.push_back(left);
return ret;
}
};搜索插入位置
思路: 当目标值存在时,明显二分就可以解决问题,当目标值不存在时,插入位置应该是恰好比它小的数的后一个位置,所以应该把数组分为两部分,一部分小于目标值,另一部分大于等于它,大于等于它的部分的第一个元素的位置就是它应该插入的位置,属于文章开头左边界的划分方式,使用左边界的模版即可解决问题。
代码:
cpp
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while(left < right){
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
if(nums[left] < target) return left + 1;
return left;
}
};x 的平方根

思路: 因为结果只保留整数部分,所以相当于最终的结果的平方要小于等于 x,所以将 1 到 x 这些数划分为两部分,一部分平方小于等于 x,一部分平方大于x,属于文章开头右边界的划分方式,使用找右端点的方式即可解决这道题。
代码:
cpp
class Solution {
public:
int mySqrt(int x) {
if(x < 1) return 0;
int left = 1;
int right = x;
while(left < right)
{
long long mid = left + (right - left + 1) / 2;
if(mid * mid > x) right = mid - 1;
else left = mid;
}
return left;
}
};山脉数组的峰顶索引

**思路:**这道题还是使用二分的方法,当 mid(中间值的下标)指向的元素小于 mid 后一个位置的元素时,最终结果一定在 mid 的右边,所以 left = mid + 1,如果 mid 指向的元素大于后一个位置的元素,当前 mid 所指向的值可能是最终结果,所以 right = mid。这个其实就是左边界的模版。
代码:
cpp
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left = 0;
int right = arr.size() - 1;
while(left < right){
int mid = left + (right - left) / 2;
if(arr[mid] < arr[mid + 1]) left = mid + 1;
else right = mid;
}
return left;
}
};寻找峰值

**思路:**和上一道题的思路是一样的,这里不在赘述。
代码:
cpp
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < nums[mid + 1]) left = mid + 1;
else right = mid;
}
return left;
}
};寻找旋转排序数组中的最小值

**思路:**这道题的思路和峰值那两道题很像,但是不能直接和 mid 前后的值进行比较判断 left,right 的变化,而是 mid 指向的元素和数组最后一个元素进行比较判断 left,right 的变化。原因如下图:(n 是数组中元素个数)
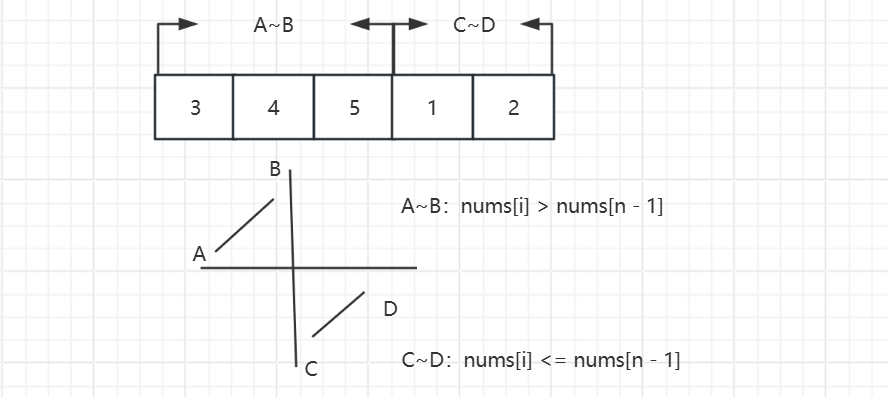
代码:
cpp
class Solution {
public:
int findMin(vector<int>& nums) {
int n = nums.size();
int left = 0;
int right = n - 1;
while(left < right){
int mid = left + (right - left) / 2;
if(nums[mid] > nums[n - 1]) left = mid + 1;
else right = mid;
}
return nums[left];
}
};LCR 173. 点名

**思路:**二分的本质其实就是在找数组的二段性,本题中数组的二段性在于前一部分数组元素和下标是对应的,而从缺失的那个元素的位置开始,数组元素和下标之间就不是一一对应的了。如图中示例1,0 元素的下标是 0, 1 元素的下标是 1......,5 元素的下标却是 4。利用这个二段性,使用二分就可以解决问题了。
代码:
cpp
class Solution {
public:
int takeAttendance(vector<int>& records) {
int left = 0;
int right = records.size() - 1;
while(left < right){
int mid = left + (right - left) / 2;
if(records[mid] == mid) left = mid + 1;
else right = mid;
}
return records[left] == left ? left + 1 : left;
}
};