【剑斩OFFER】算法的暴力美学——力扣 542 .01 题：矩阵

橘颂TA2026-01-28 13:20

一、题目描述

二、算法原理

思路：正难则反的使用 BFS

例如：

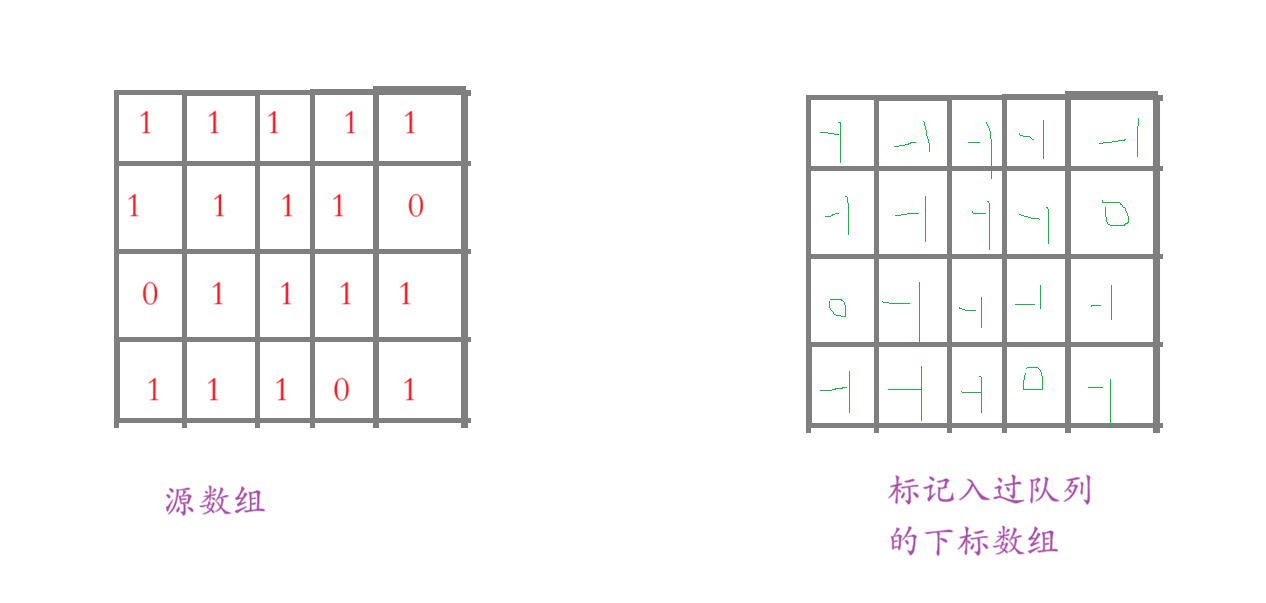
如果我们站在从 1 找 0 的思路就会导致我们写 BFS 是入队列的值超级答，所以我们站在从 0 找 1 的角度来解决这道题，为什么？既然从 1 能找 0 ，那么也能从 0 找到 1；

1）创建一个二维数组，用来标记入过队列的下标

2）找源数组中 0 的下标，并且入队列，让右边那个数组对应的下标的值 = 0

3）使用 BFS 算法，此时当前坐标的值等于层数，例如：

因为我们当前层入队列的下标都是 0 的下标，所以 0 的上上下左右的值为 1（因为层数为1）：

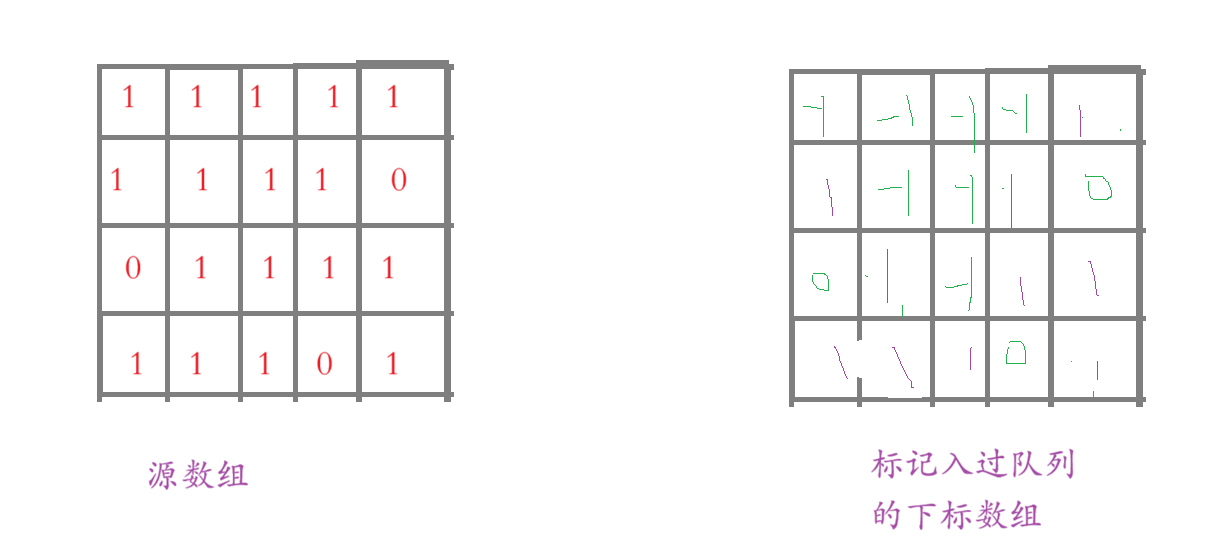
那么第二层就是 1 的上下左右的下标的值为 2，依次类推；

三、代码实现

cpp 复制代码

class Solution {
    int dx[4] = {0,0,-1,1};
    int dy[4] = {1,-1,0,0};
    typedef pair<int,int> PII;
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        vector<vector<int>> tmp(mat.size(),vector<int>(mat[0].size(),-1));//使用模拟数组来标记入队列的坐标
        queue<PII> que;
        for(int i = 0; i < mat.size(); i++)//把值为 0 的坐标入队列
        {
            for(int j = 0; j < mat[0].size(); j++)
            {
                if(mat[i][j] == 0)
                {
                    tmp[i][j] = 0;
                    que.push({i,j});
                }
            }
        }
        int sep = 0;//最小路径
        while(que.size())//使用 BFS 算法
        {
            int count = que.size();
            sep++;
            while(count--)//每扩一层的最小路径
            {
                auto [x,y] = que.front();
                que.pop();
                for(int i = 0; i < 4; i++)
                {
                    int a = x + dx[i], b = y + dy[i];
                    if(a >= 0 && b >= 0 && a < mat.size() && b < mat[0].size() && tmp[a][b] == -1)
                    {
                        tmp[a][b] = sep;//从 0 以外都是非 0 值，最终层数就是最小路径
                        que.push({a,b});
                    }
                }
            }
        }
        return tmp;
    }
};