1.递归
核心要点:构造一个函数来实现题目要实现的功能,不要去想这个函数怎么完成这个功能,就无条件相信它一定可以,之后写出递归出口,让函数自己调用自己,在做题时,不要格外关注这个递归函数的细节展开图(展开会很乱,容易把自己搞晕),无条件相信就好,就像要无条件相信自己的女朋友一样,具体步骤就是,找到相同的重复的子问题,设计函数头,随后只关注一个子问题是怎样解决的,根据此编写函数体,最后注意一下递归出口即可!!
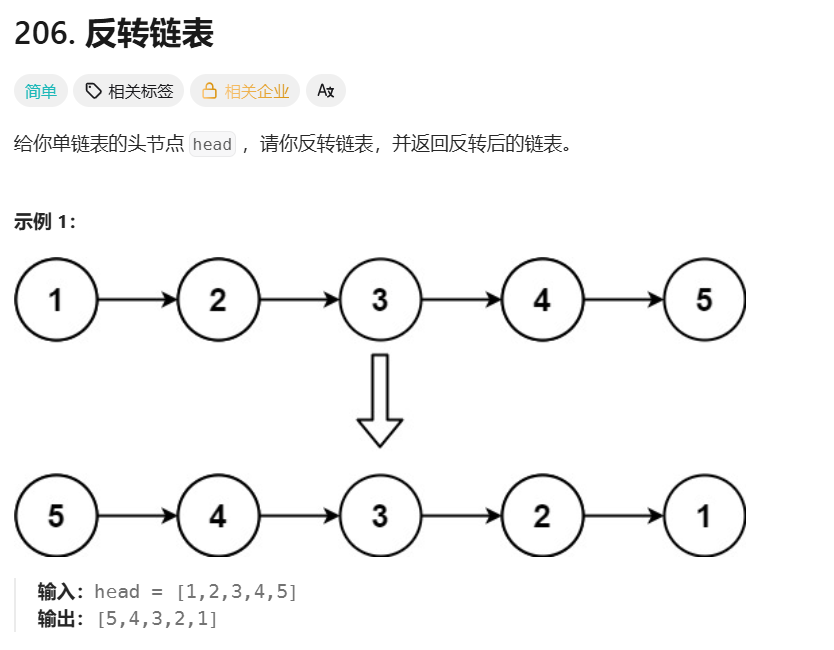
例题:反转链表
https://leetcode.cn/problems/reverse-linked-list/
题目要求:
参考代码:
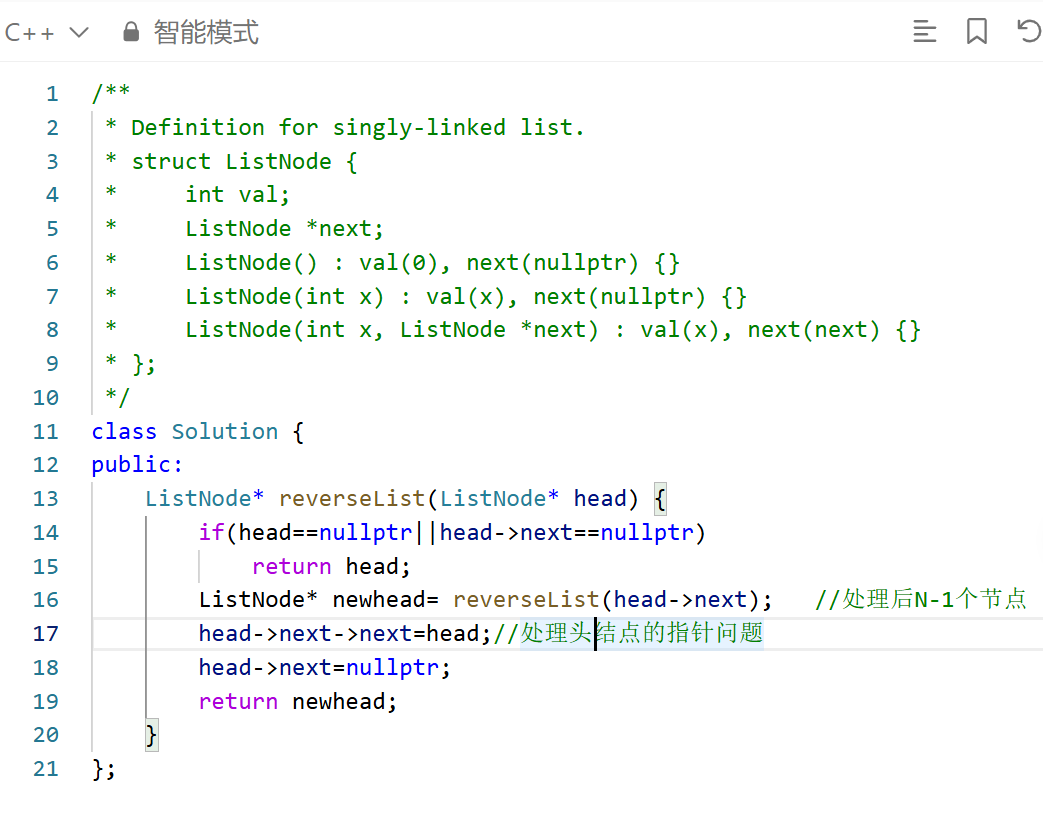
代码原理就是结合技术要点进行理解!!
2.二叉树深搜
这个就是二叉树遍历的应用,对二叉树复习一下就好,不做额外说明,仅给出例题
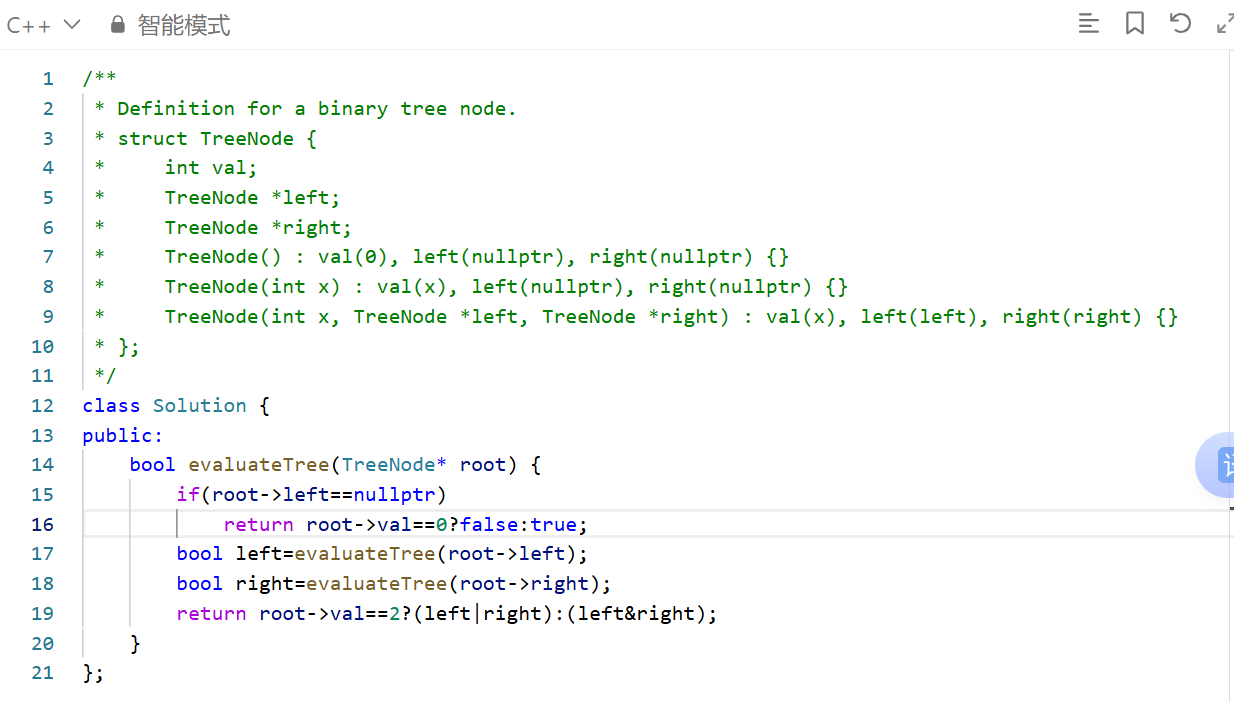
例:布尔二叉树 https://leetcode.cn/problems/evaluate-boolean-binary-tree/
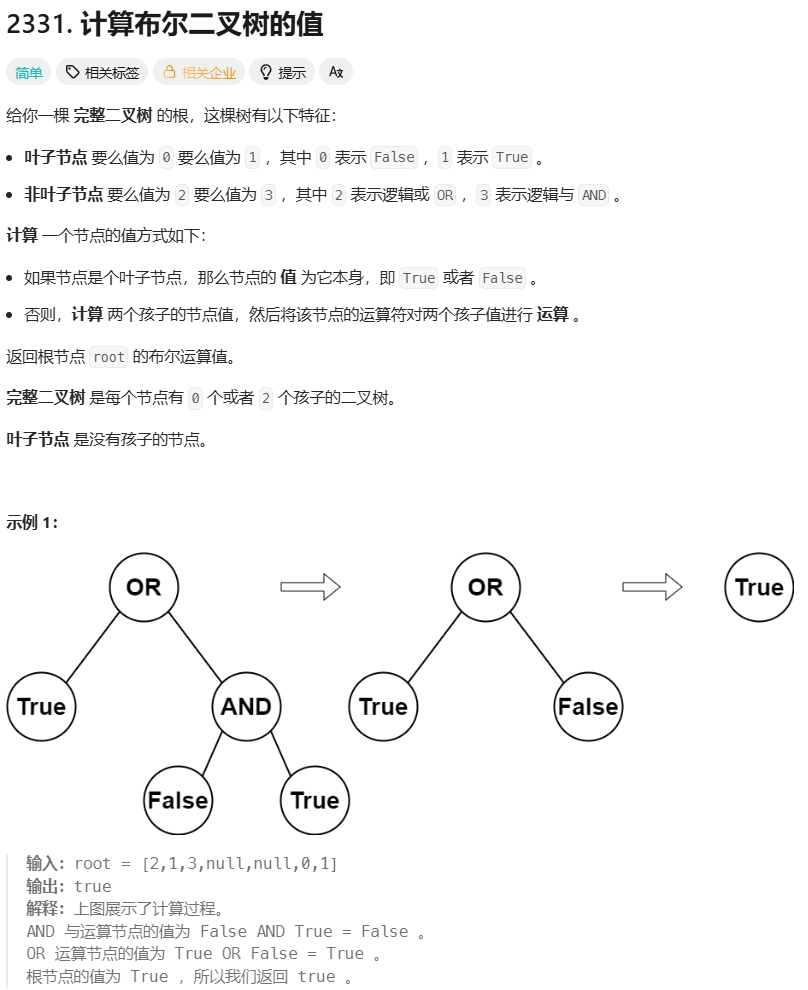
参考代码:
我们采用前序遍历
3.暴搜
这种题一般让你找出所有的可能路径或者子集之类的,所以就设置一个当前"路径"数组和最后的结果返回数组就好,其余的要通过话细节图来进行分析,抓一个局部的子问题进行分析,编写函数代码。
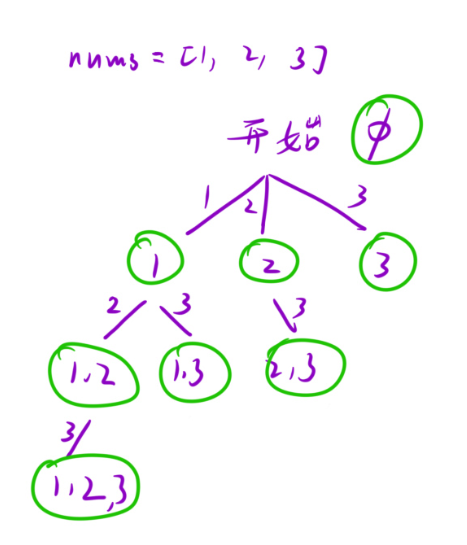
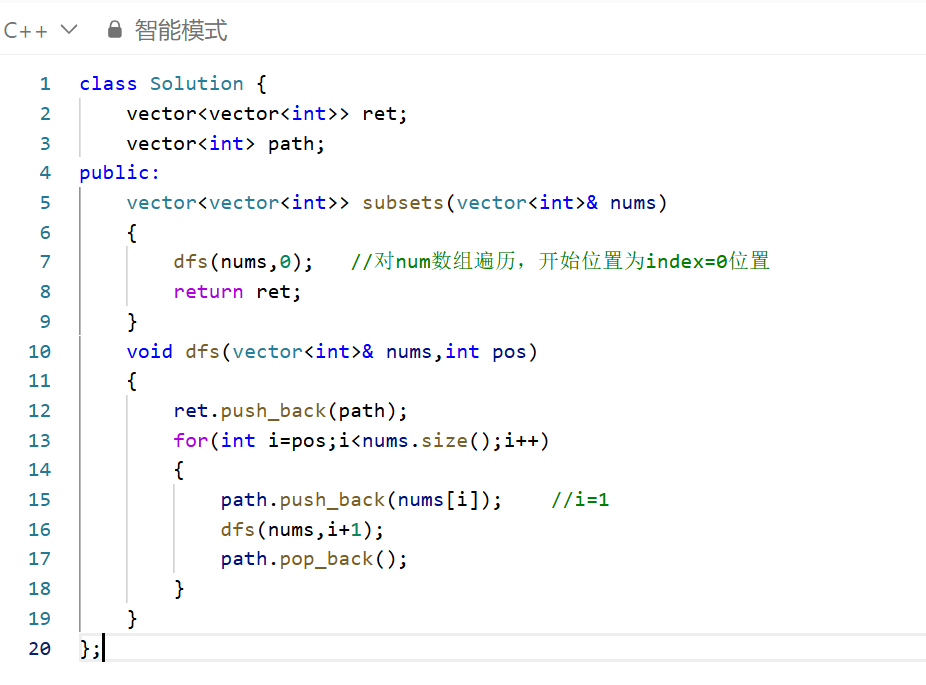
例题:全子集https://leetcode.cn/problems/subsets/

解题思路:利用排列组合知识画出分析图!我们发现所有节点就是要求的答案,因此在每次进入dfs函数之后,都要把这个"路径"加入到ret中!之后利用for 循环来确定遍历的开始位置
参考代码:
4.综合练习
这里我们做一道很常见的题型,一个二维数组,之后根据题目要求规划最优路径类型题目,解题方法就是,根据题目说的移动规则,设置出dx[]和dy[],用于控制移动,之后为了避免走回头路一直绕圈圈这种情况出现,我们可以设置一个二维的visit数组,来表示哪些位置已经走过了,随后结合题意编写代码即可~
例题:黄金矿工 https://leetcode.cn/problems/path-with-maximum-gold/

结合上述要点,应该不难写出代码!
class Solution {
bool visit[16][16];//防止走回头路
int m,n; //这里我是为了递归时少传一些参数才设置成全局变量的,大家根据自己的喜好调整即可
int dx[4]={0,0,1,-1};
int dy[4]={-1,1,0,0};
int ret;
public:
int getMaximumGold(vector<vector<int>>& g) {
m=g.size(),n=g[0].size();
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(g[i][j]!=0)
{
visit[i][j]=true;
dfs(g,i,j,g[i][j]);
visit[i][j]=false; //回溯恢复现场
}
}
}
return ret;
}
void dfs(vector<vector<int>>& g,int i,int j,int path)
{
ret=max(ret,path); //更新结果
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k]; //上下左右移动
if(x>=0 && x<m && y>=0 && y<n && !visit[x][y] && g[x][y]!=0)
{
visit[x][y]=true;
dfs(g,x,y,path+g[x][y]);
visit[x][y]=false;
}
}
}
};5.floodfill算法
本质上不难,就是例题4的那种类型,找符合题干的连通区域,做法同上
例题:最大岛屿面积
https://leetcode.cn/problems/max-area-of-island/
代码:
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int m,n;
int count=0;
int ret=0;
bool visit[51][51];
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
m=grid.size();
n=grid[0].size();
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(visit[i][j]==false && grid[i][j]==1) //没走过的陆地
{
visit[i][j]=true; //这里我走过了,不能走回头走了
count++;
dfs(grid,i,j);
count=0;
}
}
}
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j)
{
ret=max(count,ret); //更新结果
//进行上下移动探索陆地
for(int k=0;k<4;k++)
{
int x=i+dx[k];
int y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&visit[x][y]==false&&grid[x][y]==1)
//先判断是否越界在看走没走过
{
count++;
visit[x][y]=true;
dfs(grid,x,y);
visit[x][y]=false;
}
}
}
};6.记忆化搜索
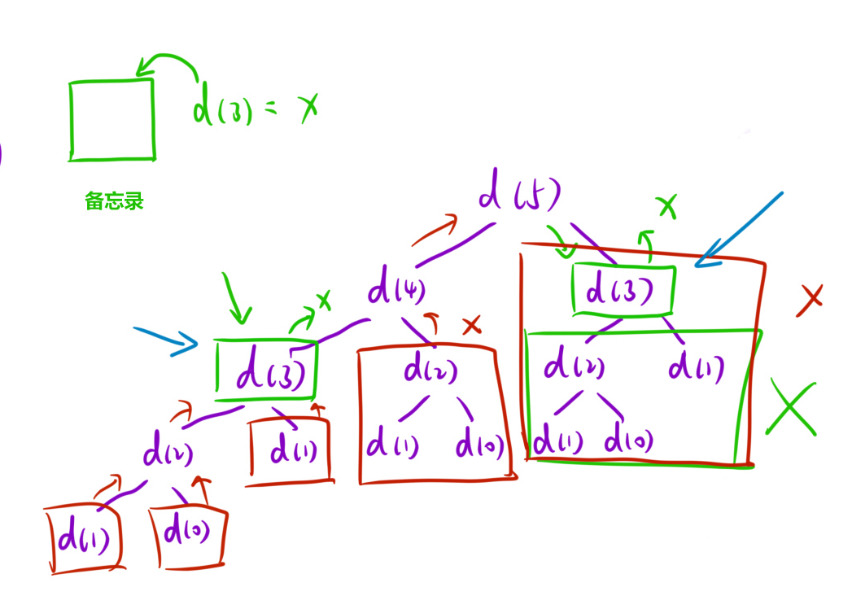
不要害怕,就给理解成带有备忘录的递归就好,就是为了降低时间复杂度才搞出来的算法,备忘录可以通过数组,哈希表等一切方式来实现,能实现"记录"功能就可以,不管黑猫白猫,能抓耗子就是好猫!参考这个,有点类似于数学里的整体带入~如下图,我们就可以把这个d(3)加入备忘录,下次用的时候不用算了~
例题:路径问题
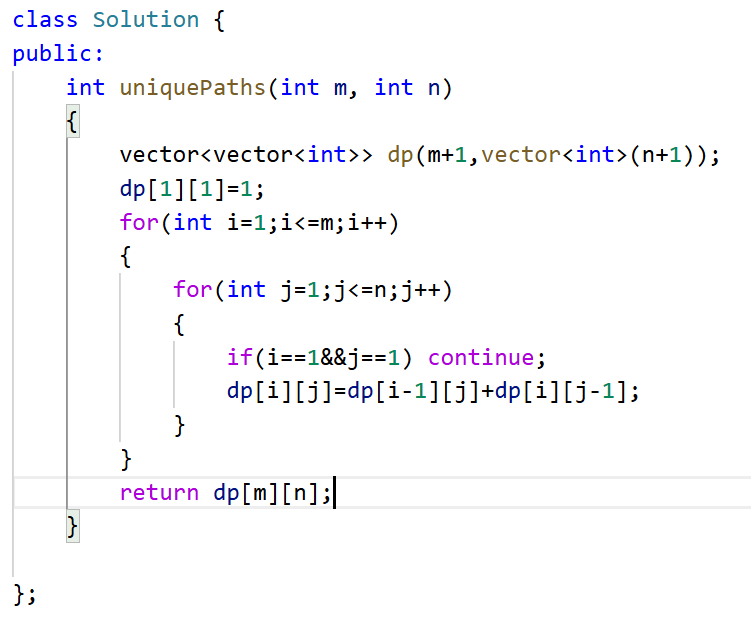
https://leetcode.cn/problems/unique-paths/
代码:
方法一:暴力搜索(会超时)
超时原因就是重复展开了很多相同的情况!!

方法二:记忆化搜索
class Solution {
public:
int uniquePaths(int m, int n)
{
vector<vector<int>> memo(m+1,vector<int>(n+1));
return dfs(m,n,memo);
}
int dfs(int i,int j,vector<vector<int>>& memo)
{
if(memo[i][j]!=0)
{
return memo[i][j];
}
if(i==0||j==0) return 0;
if(i==1&&j==1)
{
memo[1][1]=1;
return 1;
}
memo[i][j]=dfs(i,j-1,memo)+dfs(i-1,j,memo);
return memo[i][j];
}
};方法三:动态递归法(目前可以理解为把暴搜进行改造),思路差不多