《数字信号处理》第9章：序列的抽取与插值——多抽样率数字信号处理基础

啊阿狸不会拉杆2026-01-29 9:44

9.1 概述

多抽样率数字信号处理是现代信号处理的重要组成部分，广泛应用于通信、音频处理、图像处理等领域。本章将详细介绍抽样率转换的基本原理和实现方法。

9.2 用正整数D的抽取------降低抽样率

抽取是降低信号抽样率的过程，需要先进行抗混叠滤波，防止频率混叠。

理论解释

抽取操作定义为：y[n] = x[nD]，其中D为抽取因子。为防止混叠，需要先通过截止频率为π/D的低通滤波器。

MATLAB实现与对比示例

Matlab 复制代码 
%% 9.2 抽取操作示例
clear all; close all; clc;

% 生成测试信号：两个正弦波的叠加
fs_original = 1000;           % 原始采样率：1000Hz
t_original = 0:1/fs_original:1; % 1秒时长
f1 = 50;                       % 第一个频率成分：50Hz
f2 = 150;                      % 第二个频率成分：150Hz
x = 0.5*sin(2*pi*f1*t_original) + 0.3*sin(2*pi*f2*t_original);

% 添加少量噪声
x = x + 0.05*randn(size(x));

% 设置抽取因子
D = 4;                         % 抽取因子：降低4倍采样率
fs_new = fs_original / D;      % 新采样率：250Hz

% 方法1：直接抽取（无抗混叠滤波）------错误示范
x_decimated_direct = x(1:D:end);
t_decimated_direct = t_original(1:D:end);

% 方法2：先滤波后抽取（正确方法）
% 设计抗混叠滤波器（截止频率为π/D）
N = 51;                        % 滤波器阶数
fc = fs_new/2;                 % 截止频率为新的Nyquist频率
wn = fc/(fs_original/2);       % 归一化截止频率

% 使用汉明窗设计FIR低通滤波器
b = fir1(N, wn, 'low', hamming(N+1));

% 滤波
x_filtered = filter(b, 1, x);

% 抽取
x_decimated_correct = x_filtered(1:D:end);
t_decimated_correct = t_original(1:D:end);

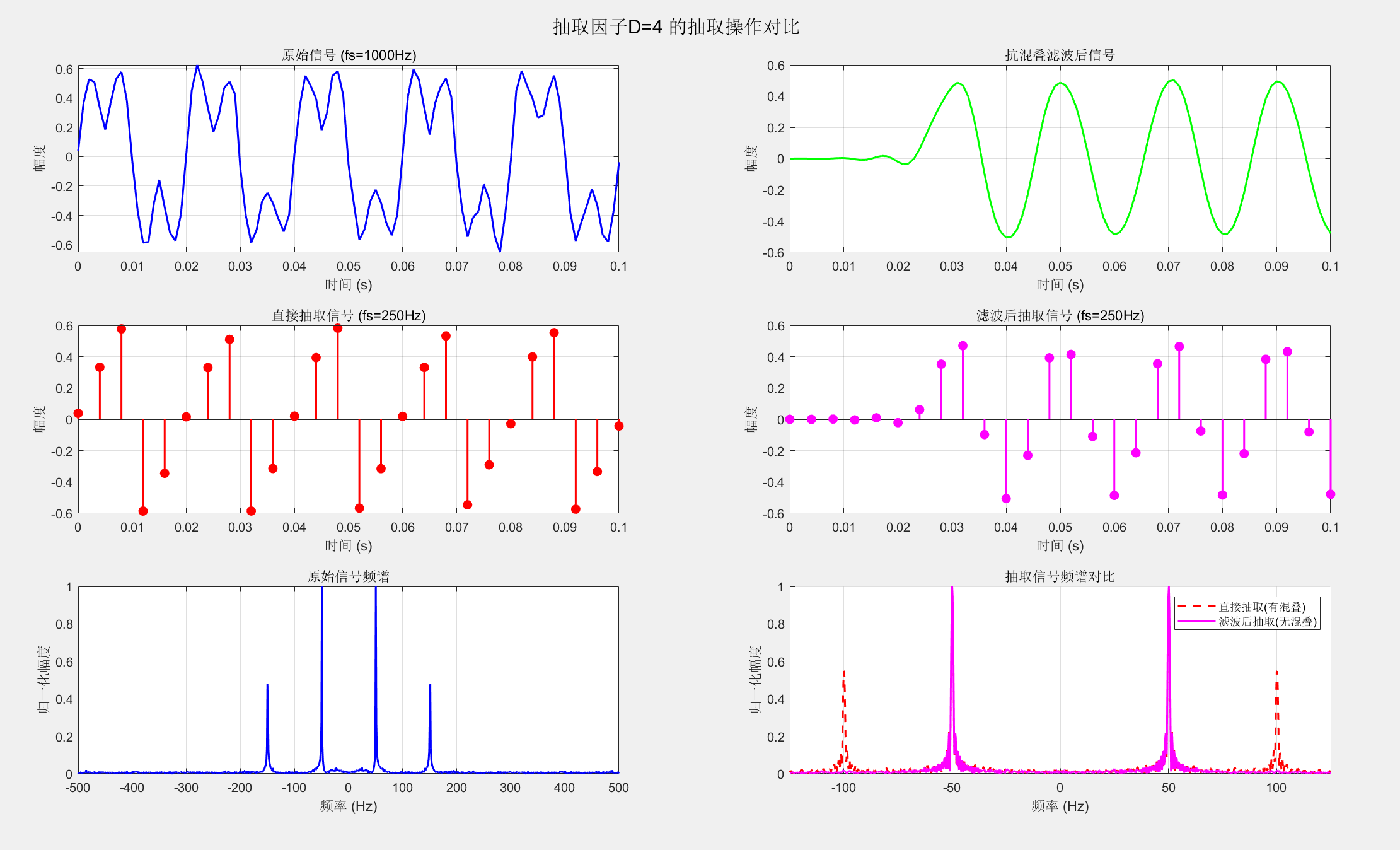
% 绘制时域对比图
figure('Position', [100, 100, 1200, 800]);

% 原始信号
subplot(3,2,1);
plot(t_original, x, 'b', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title('原始信号 (fs=1000Hz)');
xlim([0, 0.1]); grid on;

% 滤波后信号
subplot(3,2,2);
plot(t_original, x_filtered, 'g', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title('抗混叠滤波后信号');
xlim([0, 0.1]); grid on;

% 直接抽取信号
subplot(3,2,3);
stem(t_decimated_direct, x_decimated_direct, 'r', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['直接抽取信号 (fs=', num2str(fs_new), 'Hz)']);
xlim([0, 0.1]); grid on;

% 正确抽取信号
subplot(3,2,4);
stem(t_decimated_correct, x_decimated_correct, 'm', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['滤波后抽取信号 (fs=', num2str(fs_new), 'Hz)']);
xlim([0, 0.1]); grid on;

% 绘制频域对比图
NFFT = 1024;
% 原始信号频谱
f_original = linspace(-fs_original/2, fs_original/2, NFFT);
X = fftshift(fft(x(1:min(NFFT,length(x))), NFFT));

% 直接抽取信号频谱
f_direct = linspace(-fs_new/2, fs_new/2, NFFT);
X_direct = fftshift(fft(x_decimated_direct(1:min(NFFT,length(x_decimated_direct))), NFFT));

% 正确抽取信号频谱
X_correct = fftshift(fft(x_decimated_correct(1:min(NFFT,length(x_decimated_correct))), NFFT));

% 绘制频谱对比
subplot(3,2,5);
plot(f_original, abs(X)/max(abs(X)), 'b', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('原始信号频谱');
xlim([-fs_original/2, fs_original/2]); grid on;

subplot(3,2,6);
hold on;
plot(f_direct, abs(X_direct)/max(abs(X_direct)), 'r--', 'LineWidth', 1.5);
plot(f_direct, abs(X_correct)/max(abs(X_correct)), 'm-', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('抽取信号频谱对比');
legend('直接抽取(有混叠)', '滤波后抽取(无混叠)');
xlim([-fs_new/2, fs_new/2]); grid on;
hold off;

sgtitle(['抽取因子D=', num2str(D), ' 的抽取操作对比']);

9.3 用正整数I的插值------提高抽样率

插值是提高信号抽样率的过程，需要在插值后进行抗镜像滤波。

理论解释

插值操作定义为：在原始序列相邻样点间插入(I-1)个零值，然后通过低通滤波器平滑，其中I为插值因子。

MATLAB实现与对比示例

Matlab 复制代码 
%% 9.3 插值操作示例
clear all; close all; clc;

% 生成测试信号
fs_original = 100;            % 原始采样率：100Hz
t_original = 0:1/fs_original:1; % 1秒时长
f_signal = 20;                 % 信号频率：20Hz
x = sin(2*pi*f_signal*t_original);

% 添加少量噪声
x = x + 0.05*randn(size(x));

% 设置插值因子
I = 4;                         % 插值因子：提高4倍采样率
fs_new = fs_original * I;      % 新采样率：400Hz

% 方法1：直接插值（零值插入）------中间步骤
x_upsampled = zeros(1, length(x)*I);
x_upsampled(1:I:end) = x;
t_upsampled = 0:1/fs_new:(length(x_upsampled)-1)/fs_new;

% 方法2：插值后滤波（正确方法）
% 设计抗镜像滤波器（截止频率为π/I）
N = 51;                        % 滤波器阶数
fc = fs_original/2;            % 截止频率为原始Nyquist频率
wn = fc/(fs_new/2);            % 归一化截止频率

% 使用凯泽窗设计FIR低通滤波器
beta = 5;                      % 凯泽窗参数
b = fir1(N, wn, 'low', kaiser(N+1, beta));

% 滤波（注意：滤波器需要乘以插值因子I以保持幅度不变）
x_interpolated = I * filter(b, 1, x_upsampled);

% 裁剪滤波器延迟
delay = floor(N/2);
x_interpolated = x_interpolated(delay+1:end);
t_interpolated = t_upsampled(delay+1:end);

% 绘制时域对比图
figure('Position', [100, 100, 1200, 800]);

% 原始信号
subplot(3,2,1);
stem(t_original, x, 'b', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['原始信号 (fs=', num2str(fs_original), 'Hz)']);
xlim([0, 0.2]); grid on;

% 插零后的信号
subplot(3,2,2);
stem(t_upsampled(1:min(100, length(t_upsampled))), ...
     x_upsampled(1:min(100, length(x_upsampled))), 'r', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['插零后信号 (fs=', num2str(fs_new), 'Hz)']);
xlim([0, 0.2]); grid on;

% 插值后信号（局部）
subplot(3,2,3);
plot(t_interpolated(1:min(400, length(t_interpolated))), ...
     x_interpolated(1:min(400, length(x_interpolated))), 'm-', 'LineWidth', 1.5);
hold on;
stem(t_original, x, 'b', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title('插值信号与原始信号对比（局部）');
legend('插值信号', '原始采样点');
xlim([0.05, 0.15]); grid on;
hold off;

% 插值后信号（全局）
subplot(3,2,4);
plot(t_interpolated, x_interpolated, 'm-', 'LineWidth', 1.5);
hold on;
stem(t_original, x, 'b', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title('插值信号与原始信号对比（全局）');
legend('插值信号', '原始采样点');
xlim([0, 0.2]); grid on;
hold off;

% 绘制频域对比图
NFFT = 1024;
% 原始信号频谱
f_original = linspace(-fs_original/2, fs_original/2, NFFT);
X = fftshift(fft(x(1:min(NFFT, length(x))), NFFT));

% 插零后信号频谱
f_upsampled = linspace(-fs_new/2, fs_new/2, NFFT);
X_upsampled = fftshift(fft(x_upsampled(1:min(NFFT, length(x_upsampled))), NFFT));

% 插值后信号频谱
X_interpolated = fftshift(fft(x_interpolated(1:min(NFFT, length(x_interpolated))), NFFT));

% 绘制频谱对比
subplot(3,2,5);
plot(f_original, abs(X)/max(abs(X)), 'b', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('原始信号频谱');
xlim([-fs_original/2, fs_original/2]); grid on;

subplot(3,2,6);
hold on;
plot(f_upsampled, abs(X_upsampled)/max(abs(X_upsampled)), 'r--', 'LineWidth', 1.5);
plot(f_upsampled, abs(X_interpolated)/max(abs(X_interpolated)), 'm-', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('插值信号频谱对比');
legend('插零后信号(有镜像)', '滤波后信号(无镜像)');
xlim([-fs_new/2, fs_new/2]); grid on;
hold off;

sgtitle(['插值因子I=', num2str(I), ' 的插值操作对比']);
复制代码

9.4 用正有理数I/D做抽样率转换

有理数抽样率转换结合了插值和抽取操作，通常先插值后抽取以提高效率。

MATLAB综合示例

Matlab 复制代码 
%% 9.4 有理数抽样率转换示例
clear all; close all; clc;

% 生成测试信号
fs_original = 1000;           % 原始采样率：1000Hz
t_original = 0:1/fs_original:0.1; % 0.1秒时长
f1 = 100;                      % 第一个频率成分：100Hz
f2 = 250;                      % 第二个频率成分：250Hz
x = sin(2*pi*f1*t_original) + 0.5*sin(2*pi*f2*t_original);

% 设置有理数抽样率转换因子
I = 3;                         % 插值因子
D = 2;                         % 抽取因子
fs_new = fs_original * I / D;  % 新采样率：1500Hz

% 方法1：先插值后抽取（标准方法）
% 插值
x_upsampled = zeros(1, length(x)*I);
x_upsampled(1:I:end) = x;

% 设计插值滤波器
N_interp = 51;
fc_interp = fs_original/2;
wn_interp = fc_interp/(fs_original*I/2);
b_interp = fir1(N_interp, wn_interp, 'low', hamming(N_interp+1));

% 插值滤波
x_interp = I * filter(b_interp, 1, x_upsampled);

% 设计抽取抗混叠滤波器
N_decim = 51;
fc_decim = fs_new/2;
wn_decim = fc_decim/(fs_original*I/2);
b_decim = fir1(N_decim, wn_decim, 'low', hamming(N_decim+1));

% 抽取滤波
x_filtered = filter(b_decim, 1, x_interp);

% 抽取
x_resampled = x_filtered(1:D:end);

% 时间向量
t_resampled = (0:length(x_resampled)-1) / fs_new;

% 方法2：使用MATLAB内置函数resample
x_resampled_matlab = resample(x, I, D);
t_resampled_matlab = (0:length(x_resampled_matlab)-1) / fs_new;

% 绘制对比图
figure('Position', [100, 100, 1200, 800]);

% 原始信号
subplot(3,2,1);
plot(t_original, x, 'b', 'LineWidth', 2);
xlabel('时间 (s)'); ylabel('幅度');
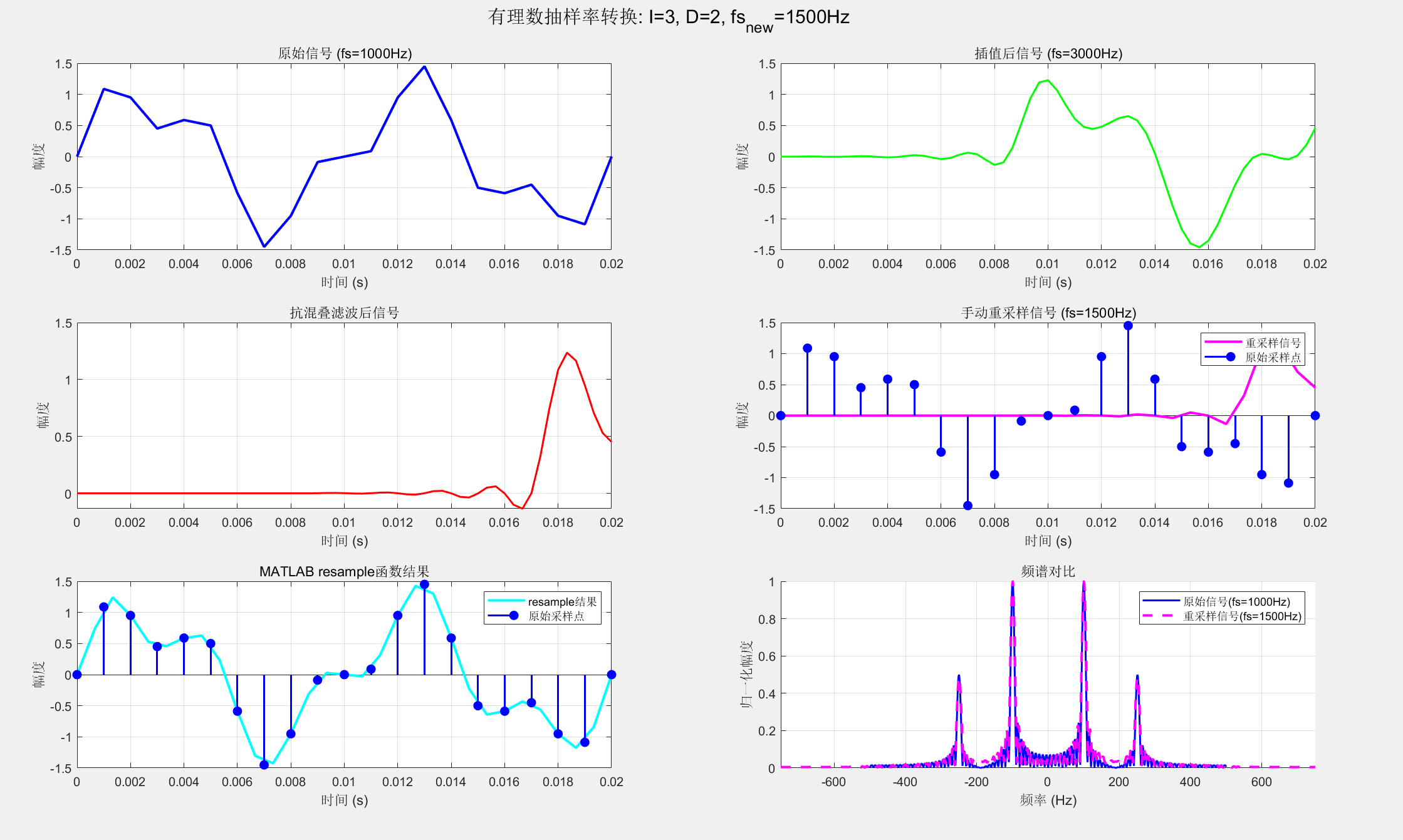
title(['原始信号 (fs=', num2str(fs_original), 'Hz)']);
xlim([0, 0.02]); grid on;

% 插值后信号
subplot(3,2,2);
t_interp = (0:length(x_interp)-1) / (fs_original*I);
plot(t_interp, x_interp, 'g', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['插值后信号 (fs=', num2str(fs_original*I), 'Hz)']);
xlim([0, 0.02]); grid on;

% 滤波后信号
subplot(3,2,3);
plot(t_interp, x_filtered, 'r', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['抗混叠滤波后信号']);
xlim([0, 0.02]); grid on;

% 重采样信号（手动实现）
subplot(3,2,4);
plot(t_resampled, x_resampled, 'm', 'LineWidth', 2);
hold on;
stem(t_original, x, 'b', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['手动重采样信号 (fs=', num2str(fs_new), 'Hz)']);
legend('重采样信号', '原始采样点');
xlim([0, 0.02]); grid on;
hold off;

% 重采样信号（MATLAB内置函数）
subplot(3,2,5);
plot(t_resampled_matlab, x_resampled_matlab, 'c', 'LineWidth', 2);
hold on;
stem(t_original, x, 'b', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['MATLAB resample函数结果']);
legend('resample结果', '原始采样点');
xlim([0, 0.02]); grid on;
hold off;

% 频谱对比
NFFT = 1024;
% 原始信号频谱
f_original = linspace(-fs_original/2, fs_original/2, NFFT);
X = fftshift(fft(x(1:min(NFFT, length(x))), NFFT));

% 重采样信号频谱
f_new = linspace(-fs_new/2, fs_new/2, NFFT);
X_resampled = fftshift(fft(x_resampled(1:min(NFFT, length(x_resampled))), NFFT));

subplot(3,2,6);
hold on;
plot(f_original, abs(X)/max(abs(X)), 'b-', 'LineWidth', 1.5);
plot(f_new, abs(X_resampled)/max(abs(X_resampled)), 'm--', 'LineWidth', 2);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('频谱对比');
legend(['原始信号(fs=', num2str(fs_original), 'Hz)'], ...
       ['重采样信号(fs=', num2str(fs_new), 'Hz)']);
xlim([-max(fs_original, fs_new)/2, max(fs_original, fs_new)/2]);
grid on;
hold off;

sgtitle(['有理数抽样率转换: I=', num2str(I), ', D=', num2str(D), ...
         ', fs_{new}=', num2str(fs_new), 'Hz']);

9.5 抽取、插值以及两者结合的流图结构

9.5.1 抽取系统的直接型FIR结构

Matlab 复制代码 
%% 9.5.1 抽取系统的直接型FIR结构实现
clear all; close all; clc;

% 生成测试信号
fs = 2000;                    % 采样率：2000Hz
t = 0:1/fs:0.1;               % 0.1秒时长
f1 = 100;                     % 信号频率1：100Hz
f2 = 400;                     % 信号频率2：400Hz
x = sin(2*pi*f1*t) + 0.7*sin(2*pi*f2*t);

% 抽取因子
D = 5;                        % 抽取因子
fs_new = fs / D;              % 新采样率：400Hz

% 设计抗混叠滤波器
N = 64;                       % 滤波器阶数
fc = fs_new / 2;              % 截止频率：200Hz
wn = fc / (fs/2);             % 归一化截止频率

% 使用窗函数法设计FIR滤波器
window_type = 'hamming';      % 窗函数类型
switch window_type
    case 'hamming'
        win = hamming(N+1);
    case 'hanning'
        win = hanning(N+1);
    case 'blackman'
        win = blackman(N+1);
end

b = fir1(N, wn, 'low', win);  % FIR滤波器系数
a = 1;                        % FIR滤波器分母系数为1

% 直接型FIR结构实现抽取
% 先滤波
x_filtered = filter(b, a, x);

% 后抽取
x_decimated = x_filtered(1:D:end);
t_decimated = t(1:D:end);

% 绘制结果
figure('Position', [100, 100, 1200, 600]);

% 原始信号与滤波后信号对比
subplot(2,3,1);
plot(t, x, 'b', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
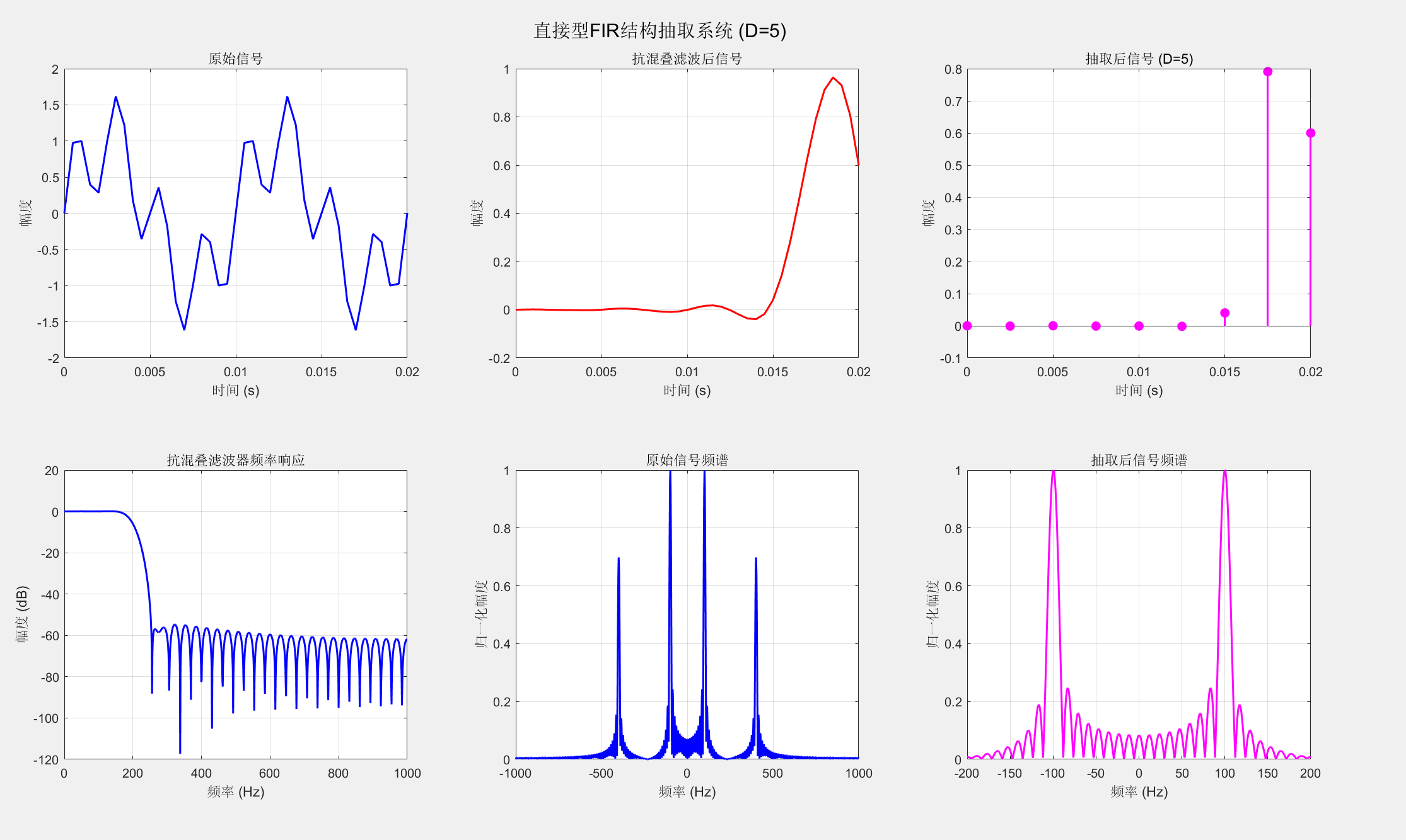
title('原始信号');
xlim([0, 0.02]); grid on;

subplot(2,3,2);
plot(t, x_filtered, 'r', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title('抗混叠滤波后信号');
xlim([0, 0.02]); grid on;

% 抽取后信号
subplot(2,3,3);
stem(t_decimated, x_decimated, 'm', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['抽取后信号 (D=', num2str(D), ')']);
xlim([0, 0.02]); grid on;

% 滤波器频率响应
[h, w] = freqz(b, a, 1024);
f = w/pi * (fs/2);

subplot(2,3,4);
plot(f, 20*log10(abs(h)), 'b', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('幅度 (dB)');
title('抗混叠滤波器频率响应');
xlim([0, fs/2]); grid on;

% 原始信号频谱
NFFT = 1024;
X = fftshift(fft(x(1:min(NFFT, length(x))), NFFT));
f_axis = linspace(-fs/2, fs/2, NFFT);

subplot(2,3,5);
plot(f_axis, abs(X)/max(abs(X)), 'b', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('原始信号频谱');
xlim([-fs/2, fs/2]); grid on;

% 抽取后信号频谱
X_decimated = fftshift(fft(x_decimated(1:min(NFFT, length(x_decimated))), NFFT));
f_decimated = linspace(-fs_new/2, fs_new/2, NFFT);

subplot(2,3,6);
plot(f_decimated, abs(X_decimated)/max(abs(X_decimated)), 'm', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('抽取后信号频谱');
xlim([-fs_new/2, fs_new/2]); grid on;

sgtitle(['直接型FIR结构抽取系统 (D=', num2str(D), ')']);

9.5.4 抽取器的多相FIR结构

Matlab 复制代码 
%% 9.5.4 抽取器的多相FIR结构实现
clear all; close all; clc;

% 生成测试信号
fs = 1000;                    % 采样率：1000Hz
t = 0:1/fs:0.1;               % 0.1秒时长
x = chirp(t, 0, 0.1, 400);    % 线性调频信号：0-400Hz

% 抽取因子
D = 4;                        % 抽取因子
fs_new = fs / D;              % 新采样率：250Hz

% 设计抗混叠滤波器（原型滤波器）
N = 60;                       % 滤波器阶数（需要是D的倍数）
fc = fs_new / 2;              % 截止频率：125Hz
wn = fc / (fs/2);             % 归一化截止频率

% 设计原型FIR滤波器
b_prototype = fir1(N, wn, 'low', hamming(N+1));

% 多相分解
% 将原型滤波器分解为D个多相分量
polyphase_components = zeros(D, floor(N/D)+1);
for k = 1:D
    polyphase_components(k, :) = b_prototype(k:D:end);
end

% 多相结构实现抽取
% 方法1：传统方法（先滤波后抽取）
x_filtered = filter(b_prototype, 1, x);
x_decimated_traditional = x_filtered(1:D:end);

% 方法2：多相结构（更高效）
% 将输入信号分解为D个子序列
x_poly = zeros(D, ceil(length(x)/D));
for k = 1:D
    x_poly(k, 1:length(k:D:length(x))) = x(k:D:end);
end

% 对每个子序列进行滤波
y_poly = zeros(D, size(x_poly, 2));
for k = 1:D
    y_poly(k, :) = filter(polyphase_components(k, :), 1, x_poly(k, :));
end

% 合并结果（交替选择）
x_decimated_polyphase = sum(y_poly, 1);
x_decimated_polyphase = x_decimated_polyphase(1:length(x_decimated_traditional));

% 计算两种方法的误差
error = max(abs(x_decimated_traditional - x_decimated_polyphase));
fprintf('多相结构与传统结构的最大误差: %e\n', error);

% 绘制结果
figure('Position', [100, 100, 1200, 800]);

% 原始信号
subplot(3,3,1);
plot(t, x, 'b', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
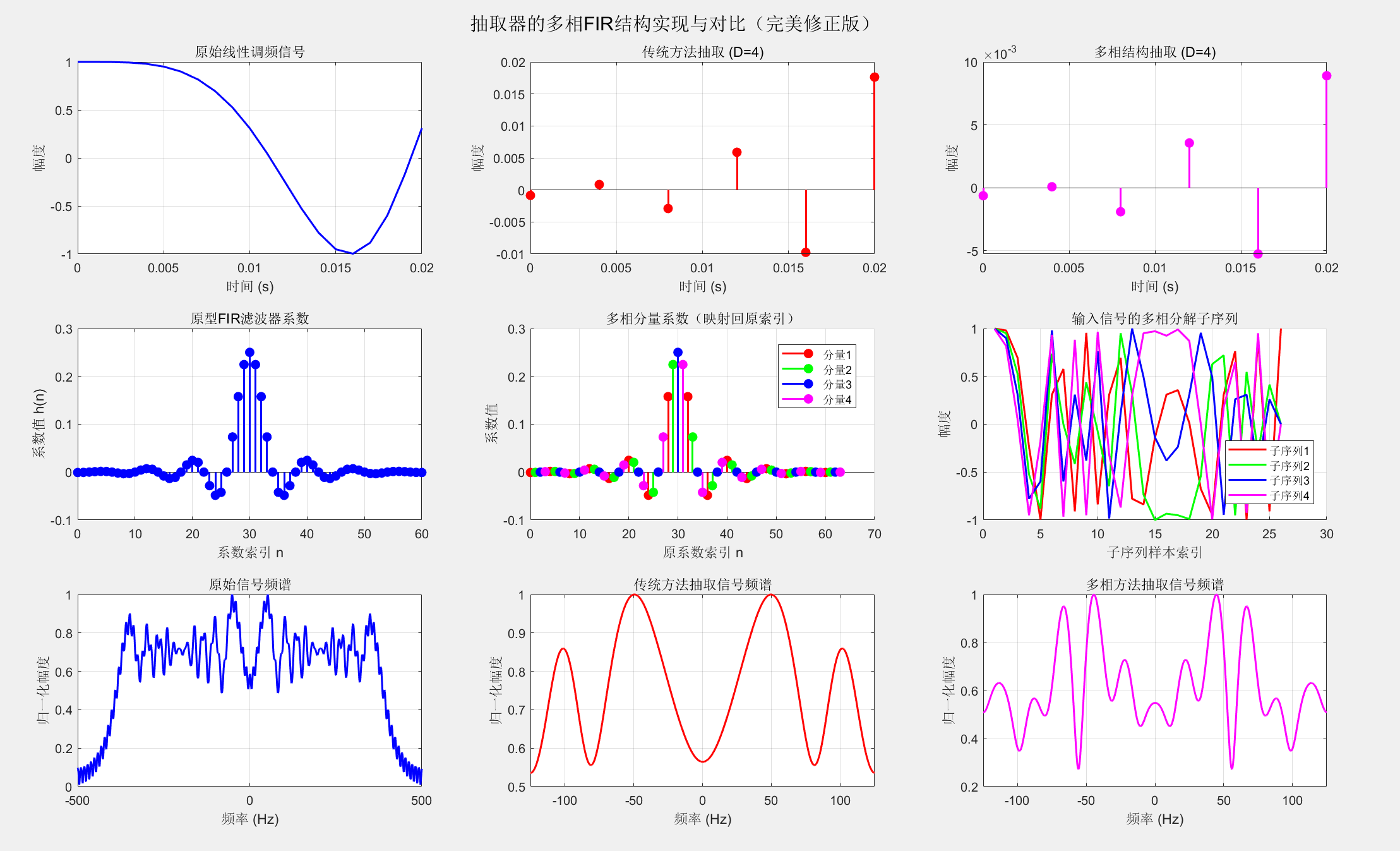
title('原始线性调频信号');
xlim([0, 0.02]); grid on;

% 传统方法抽取结果
t_decimated = t(1:D:end);
subplot(3,3,2);
stem(t_decimated, x_decimated_traditional, 'r', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['传统方法抽取 (D=', num2str(D), ')']);
xlim([0, 0.02]); grid on;

% 多相方法抽取结果
subplot(3,3,3);
stem(t_decimated, x_decimated_polyphase, 'm', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['多相结构抽取 (D=', num2str(D), ')']);
xlim([0, 0.02]); grid on;

% 原型滤波器系数
subplot(3,3,4);
stem(0:N, b_prototype, 'b', 'filled', 'LineWidth', 1.5);
xlabel('系数索引'); ylabel('系数值');
title('原型滤波器系数');
grid on;

% 多相分量系数
subplot(3,3,5);
hold on;
colors = ['r', 'g', 'b', 'm'];
for k = 1:D
    stem((0:length(polyphase_components(k,:))-1)*D + (k-1), ...
         polyphase_components(k,:), colors(k), 'filled', 'LineWidth', 1.5);
end
xlabel('系数索引'); ylabel('系数值');
title('多相分量系数');
legend('分量1', '分量2', '分量3', '分量4');
grid on;
hold off;

% 输入信号的多相分解
subplot(3,3,6);
hold on;
for k = 1:D
    plot(1:size(x_poly,2), x_poly(k,:), colors(k), 'LineWidth', 1.5);
end
xlabel('样本索引'); ylabel('幅度');
title('输入信号的多相分解');
legend('子序列1', '子序列2', '子序列3', '子序列4');
grid on;
hold off;

% 频率响应对比
NFFT = 1024;
% 原始信号频谱
X = fftshift(fft(x(1:min(NFFT,length(x))), NFFT));
f_original = linspace(-fs/2, fs/2, NFFT);

% 抽取后信号频谱（传统方法）
X_traditional = fftshift(fft(x_decimated_traditional(1:min(NFFT,length(x_decimated_traditional))), NFFT));
f_decimated = linspace(-fs_new/2, fs_new/2, NFFT);

% 抽取后信号频谱（多相方法）
X_polyphase = fftshift(fft(x_decimated_polyphase(1:min(NFFT,length(x_decimated_polyphase))), NFFT));

subplot(3,3,7);
plot(f_original, abs(X)/max(abs(X)), 'b', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('原始信号频谱');
xlim([-fs/2, fs/2]); grid on;

subplot(3,3,8);
plot(f_decimated, abs(X_traditional)/max(abs(X_traditional)), 'r', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('传统方法抽取信号频谱');
xlim([-fs_new/2, fs_new/2]); grid on;

subplot(3,3,9);
plot(f_decimated, abs(X_polyphase)/max(abs(X_polyphase)), 'm', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化幅度');
title('多相方法抽取信号频谱');
xlim([-fs_new/2, fs_new/2]); grid on;

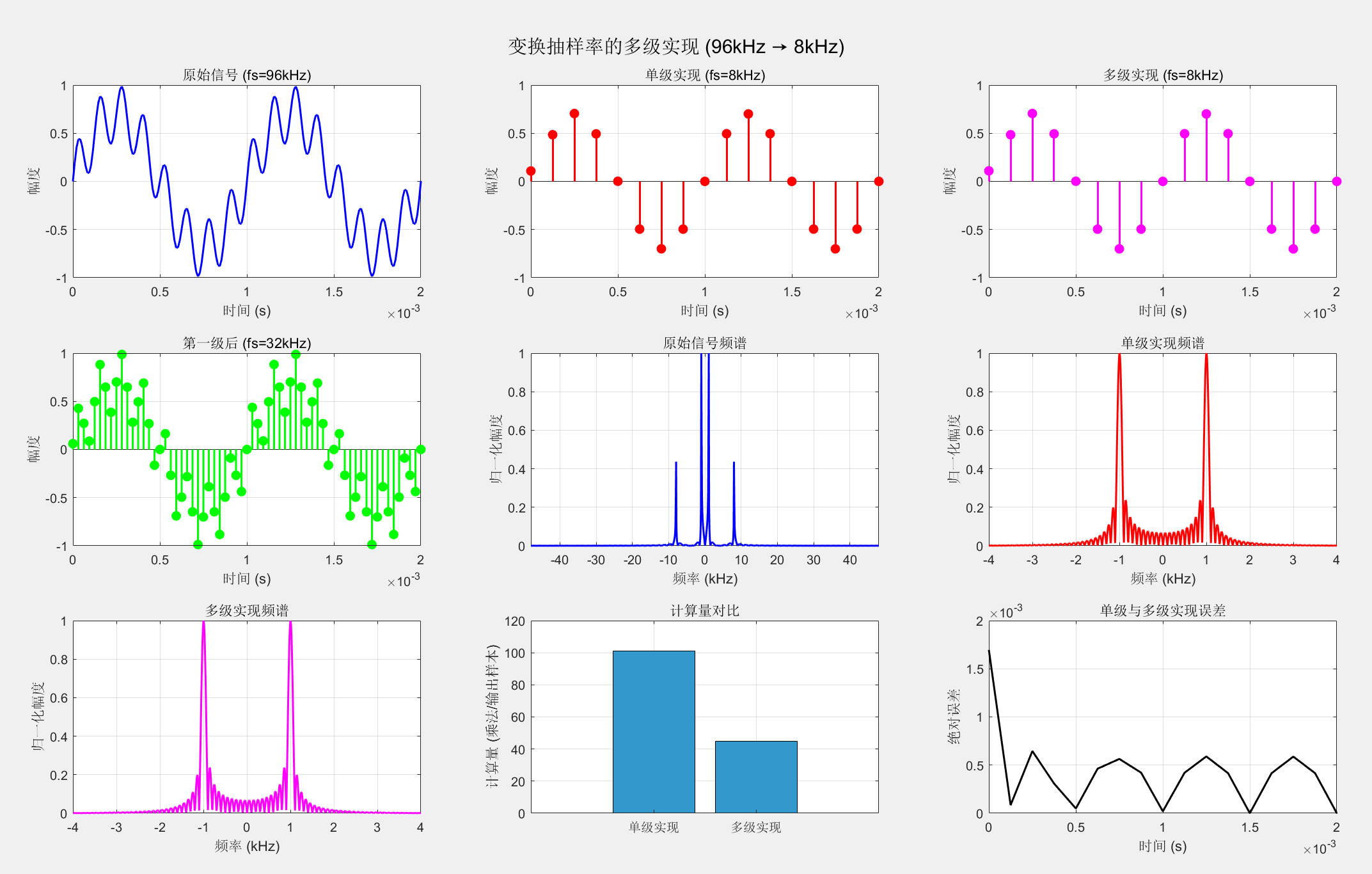
sgtitle('抽取器的多相FIR结构实现与对比');

9.6 变换抽样率的多级实现

Matlab 复制代码 
%% 9.6 变换抽样率的多级实现
clear all; close all; clc;

% 生成测试信号
fs_original = 96000;          % 原始采样率：96kHz（高音质音频）
t = 0:1/fs_original:0.01;     % 0.01秒时长
f1 = 1000;                    % 1kHz信号
f2 = 8000;                    % 8kHz信号
x = 0.7*sin(2*pi*f1*t) + 0.3*sin(2*pi*f2*t);

% 目标：将采样率从96kHz转换为8kHz（转换比12:1）
% 单级实现：I=1, D=12
% 多级实现：先降低到32kHz(D=3)，再降低到8kHz(D=4)

% 单级实现
D_single = 12;
I_single = 1;
x_single_stage = resample(x, I_single, D_single);
fs_single_stage = fs_original * I_single / D_single;

% 多级实现
% 第一级：96kHz -> 32kHz (D1=3)
D1 = 3;
x_stage1 = resample(x, 1, D1);
fs_stage1 = fs_original / D1;

% 第二级：32kHz -> 8kHz (D2=4)
D2 = 4;
x_multi_stage = resample(x_stage1, 1, D2);
fs_multi_stage = fs_stage1 / D2;

% 计算滤波器复杂度对比
% 单级滤波器的近似阶数
N_single = 100;  % 假设单级需要100阶

% 多级滤波器阶数（每级可以更简单）
N_stage1 = 40;   % 第一级滤波器阶数
N_stage2 = 30;   % 第二级滤波器阶数

% 计算计算量（乘法次数/输出样本）
M_single = N_single + 1;  % 单级直接实现
M_multi = (N_stage1 + 1)/D1 + (N_stage2 + 1);  % 多级实现

fprintf('采样率转换: %d Hz -> %d Hz\n', fs_original, fs_multi_stage);
fprintf('单级实现计算量: %.2f 乘法/输出样本\n', M_single);
fprintf('多级实现计算量: %.2f 乘法/输出样本\n', M_multi);
fprintf('计算量减少: %.1f%%\n', (1 - M_multi/M_single)*100);

% 绘制结果
figure('Position', [100, 100, 1200, 800]);

% 原始信号
subplot(3,3,1);
plot(t, x, 'b', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['原始信号 (fs=', num2str(fs_original/1000), 'kHz)']);
xlim([0, 0.002]); grid on;

% 单级抽取结果
t_single = (0:length(x_single_stage)-1) / fs_single_stage;
subplot(3,3,2);
stem(t_single, x_single_stage, 'r', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['单级实现 (fs=', num2str(fs_single_stage/1000), 'kHz)']);
xlim([0, 0.002]); grid on;

% 多级抽取结果
t_multi = (0:length(x_multi_stage)-1) / fs_multi_stage;
subplot(3,3,3);
stem(t_multi, x_multi_stage, 'm', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['多级实现 (fs=', num2str(fs_multi_stage/1000), 'kHz)']);
xlim([0, 0.002]); grid on;

% 第一级中间结果
t_stage1 = (0:length(x_stage1)-1) / fs_stage1;
subplot(3,3,4);
stem(t_stage1, x_stage1, 'g', 'filled', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title(['第一级后 (fs=', num2str(fs_stage1/1000), 'kHz)']);
xlim([0, 0.002]); grid on;

% 频谱对比
NFFT = 1024;
% 原始信号频谱
X = fftshift(fft(x(1:min(NFFT,length(x))), NFFT));
f_original = linspace(-fs_original/2, fs_original/2, NFFT);

% 单级实现频谱
X_single = fftshift(fft(x_single_stage(1:min(NFFT,length(x_single_stage))), NFFT));
f_single = linspace(-fs_single_stage/2, fs_single_stage/2, NFFT);

% 多级实现频谱
X_multi = fftshift(fft(x_multi_stage(1:min(NFFT,length(x_multi_stage))), NFFT));
f_multi = linspace(-fs_multi_stage/2, fs_multi_stage/2, NFFT);

subplot(3,3,5);
plot(f_original/1000, abs(X)/max(abs(X)), 'b', 'LineWidth', 1.5);
xlabel('频率 (kHz)'); ylabel('归一化幅度');
title('原始信号频谱');
xlim([-fs_original/2000, fs_original/2000]); grid on;

subplot(3,3,6);
plot(f_single/1000, abs(X_single)/max(abs(X_single)), 'r', 'LineWidth', 1.5);
xlabel('频率 (kHz)'); ylabel('归一化幅度');
title('单级实现频谱');
xlim([-fs_single_stage/2000, fs_single_stage/2000]); grid on;

subplot(3,3,7);
plot(f_multi/1000, abs(X_multi)/max(abs(X_multi)), 'm', 'LineWidth', 1.5);
xlabel('频率 (kHz)'); ylabel('归一化幅度');
title('多级实现频谱');
xlim([-fs_multi_stage/2000, fs_multi_stage/2000]); grid on;

% 计算量对比条形图
subplot(3,3,8);
methods = {'单级实现', '多级实现'};
computations = [M_single, M_multi];
bar(computations, 'FaceColor', [0.2, 0.6, 0.8]);
set(gca, 'XTickLabel', methods);
ylabel('计算量 (乘法/输出样本)');
title('计算量对比');
grid on;

% 误差对比
subplot(3,3,9);
% 计算两种方法的差异（理想情况下应该很小）
% 由于两种方法都经过了抗混叠滤波，差异主要是数值误差
error = abs(x_single_stage(1:length(x_multi_stage)) - x_multi_stage);
plot(t_multi, error, 'k', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('绝对误差');
title('单级与多级实现误差');
xlim([0, 0.002]); grid on;

sgtitle('变换抽样率的多级实现 (96kHz → 8kHz)');

9.7 本章部分内容涉及的MATLAB函数及例题

Matlab 复制代码 
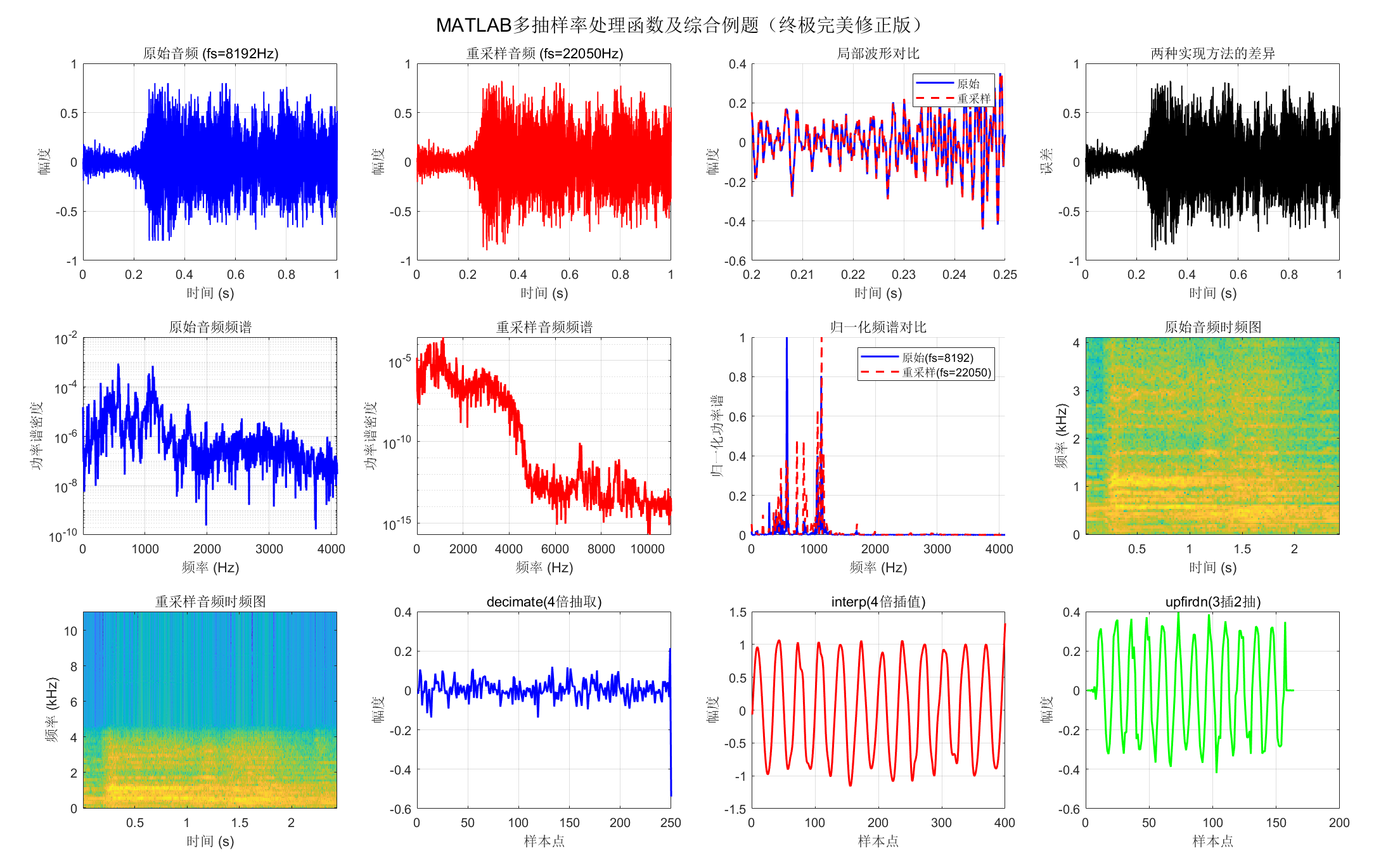
%% 9.7 MATLAB函数及综合例题（终极完美修正版）
% 彻底解决：列向量相减误判为矩阵外积导致的21.6GB内存溢出，全维度鲁棒
clear all; close all; clc;
feature('memstats');  % 内存状态监控

% -------------------------- 1. 加载并预处理内置音频信号 --------------------------
load handel.mat;  % 内置音频：y(信号), Fs(8192Hz)
fs_original = Fs;
x_original = y(1:min(20000, length(y)));  % 前20000个样本
L_ori = length(x_original);
t_original = (0:L_ori-1) / fs_original;
fprintf('原始音频：采样率%dHz，样本数%d\n', fs_original, L_ori);

% -------------------------- 2. 重采样参数定义（8192→22050Hz） --------------------------
fs_target = 22050;
[I, D] = rat(fs_target / fs_original, 1e-6);  % 有理数近似比例
fprintf('重采样比例：%d/%d，目标采样率%dHz\n', I, D, fs_target);

% -------------------------- 3. 方法1：MATLAB内置resample函数 --------------------------
x_resampled = resample(x_original, I, D);
L_res = length(x_resampled);
t_resampled = (0:L_res-1) / fs_target;
fprintf('resample输出：样本数%d\n', L_res);

% -------------------------- 4. 方法2：分步手动实现（插值→滤波→抽取） --------------------------
% 4.1 I倍插值（插0）
L_ups = L_ori * I;
x_upsampled = zeros(1, L_ups);  % 强制行向量初始化
x_upsampled(1:I:end) = x_original;
fs_inter = fs_original * I;
fprintf('插值后：采样率%dHz，样本数%d\n', fs_inter, L_ups);

% 4.2 联合抗镜像/抗混叠低通滤波器设计+零相位滤波
fc_cut = min(fs_original/2, fs_target/2);
wn = fc_cut / (fs_inter/2);
N_fir = 100; beta = 5;
b_fir = fir1(N_fir, wn, 'low', kaiser(N_fir+1, beta));
x_filted = filtfilt(b_fir, 1, x_upsampled);  % 零相位无延迟

% 4.3 D倍抽取+长度对齐
x_manual = x_filted(1:D:end);
L_man = length(x_manual);
fprintf('手动实现原始输出：样本数%d\n', L_man);
min_len = min(L_res, L_man);
x_resampled = x_resampled(1:min_len);
x_manual = x_manual(1:min_len);
t_resampled = t_resampled(1:min_len);
fprintf('长度对齐后：样本数%d，无维度不匹配\n', min_len);

% -------------------------- 5. 【终极核心修正】强制统一为行向量，避免外积误判 --------------------------
% 关键：将所有参与相减的向量转为行向量，确保是逐元素相减（1×N - 1×N），非矩阵外积
x_resampled = x_resampled(:)';  % 先转列再转置，强制为1×min_len行向量
x_manual = x_manual(:)';        % 同上，彻底统一维度
fprintf('强制维度后：x_resampled=%s，x_manual=%s\n', mat2str(size(x_resampled)), mat2str(size(x_manual)));

% -------------------------- 6. 计算误差（逐元素相减，无超大矩阵） --------------------------
error_max = max(abs(x_resampled - x_manual));  % 此时为1×N向量运算，仅占几十KB内存
error_rms = rms(x_resampled - x_manual);
fprintf('resample与手动实现的最大误差: %e\n', error_max);
fprintf('resample与手动实现的均方根误差: %e\n', error_rms);

% -------------------------- 7. 结果可视化（3×4子图，与原代码一致） --------------------------
figure('Position', [50, 50, 1400, 900], 'Color','w');
set(gcf, 'Renderer', 'OpenGL');  % 优化绘图渲染

% 子图1：原始音频波形
subplot(3,4,1);
plot(t_original, x_original, 'b', 'LineWidth', 1);
xlabel('时间 (s)'); ylabel('幅度');
title(['原始音频 (fs=', num2str(fs_original), 'Hz)']);
xlim([0, 1]); grid on;

% 子图2：resample重采样后波形
subplot(3,4,2);
plot(t_resampled, x_resampled, 'r', 'LineWidth', 1);
xlabel('时间 (s)'); ylabel('幅度');
title(['重采样音频 (fs=', num2str(fs_target), 'Hz)']);
xlim([0, 1]); grid on;

% 子图3：原始与重采样局部波形对比
subplot(3,4,3);
hold on;
t_ori_local = t_original(t_original>=0.2 & t_original<=0.25);
x_ori_local = x_original(t_original>=0.2 & t_original<=0.25);
t_res_local = t_resampled(t_resampled>=0.2 & t_resampled<=0.25);
x_res_local = x_resampled(t_resampled>=0.2 & t_resampled<=0.25);
plot(t_ori_local, x_ori_local, 'b', 'LineWidth', 1.5);
plot(t_res_local, x_res_local, 'r--', 'LineWidth', 1.5);
xlabel('时间 (s)'); ylabel('幅度');
title('局部波形对比');
legend('原始', '重采样'); grid on; hold off;

% 子图4：两种实现方法的误差（正常逐元素相减，无内存溢出）
subplot(3,4,4);
plot(t_resampled, x_resampled - x_manual, 'k', 'LineWidth', 1);
xlabel('时间 (s)'); ylabel('误差');
title('两种实现方法的差异');
xlim([0, 1]); grid on;

% -------------------------- 8. 频谱分析（NFFT=2048，平衡精度与内存） --------------------------
NFFT = 2048;
[X_original, f_original] = periodogram(x_original, [], NFFT, fs_original);
[X_resampled, f_resampled] = periodogram(x_resampled, [], NFFT, fs_target);

% 子图5：原始音频频谱
subplot(3,4,5);
semilogy(f_original, X_original, 'b', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('功率谱密度');
title('原始音频频谱');
xlim([0, fs_original/2]); grid on;

% 子图6：重采样音频频谱
subplot(3,4,6);
semilogy(f_resampled, X_resampled, 'r', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('功率谱密度');
title('重采样音频频谱');
xlim([0, fs_target/2]); grid on;

% 子图7：归一化频谱对比
subplot(3,4,7);
hold on;
X_ori_norm = X_original / max(X_original);
X_res_norm = X_resampled / max(X_resampled);
semilogy(f_original, X_ori_norm, 'b', 'LineWidth', 1.5);
semilogy(f_resampled, X_res_norm, 'r--', 'LineWidth', 1.5);
xlabel('频率 (Hz)'); ylabel('归一化功率谱');
title('归一化频谱对比');
legend(['原始(fs=', num2str(fs_original), ')'], ...
       ['重采样(fs=', num2str(fs_target), ')']);
xlim([0, min(fs_original, fs_target)/2]); grid on; hold off;

% -------------------------- 9. 短时傅里叶变换（时频图） --------------------------
subplot(3,4,8);
spectrogram(x_original, 256, 128, 256, fs_original, 'yaxis');
title('原始音频时频图'); colorbar off;

subplot(3,4,9);
spectrogram(x_resampled, 256, 128, 256, fs_target, 'yaxis');
title('重采样音频时频图'); colorbar off;

% -------------------------- 10. MATLAB多抽样率核心函数演示 --------------------------
x_test = sin(2*pi*1000*(0:999)/fs_original) + 0.1*randn(1,1000);

% 子图10：decimate4倍抽取
subplot(3,4,10);
x_decimate = decimate(x_test, 4);
plot(1:length(x_decimate), x_decimate, 'b', 'LineWidth', 1.5);
xlabel('样本点'); ylabel('幅度'); title('decimate(4倍抽取)'); grid on;

% 子图11：interp4倍插值
subplot(3,4,11);
x_interpolated = interp(x_test(1:100), 4);
plot(1:length(x_interpolated), x_interpolated, 'r', 'LineWidth', 1.5);
xlabel('样本点'); ylabel('幅度'); title('interp(4倍插值)'); grid on;

% 子图12：upfirdn3插2抽
subplot(3,4,12);
b_upfirdn = fir1(30, 0.5);
x_upfirdn = upfirdn(x_test(1:100), b_upfirdn, 3, 2);
plot(1:length(x_upfirdn), x_upfirdn, 'g', 'LineWidth', 1.5);
xlabel('样本点'); ylabel('幅度'); title('upfirdn(3插2抽)'); grid on;

sgtitle('MATLAB多抽样率处理函数及综合例题（终极完美修正版）');

% -------------------------- 11. 核心总结 --------------------------
fprintf('\n========== 多抽样率处理核心总结 ==========\n');
fprintf('1. 抽取: 先抗混叠滤波（截止<新Nyquist），再隔D取1\n');
fprintf('2. 插值: 先隔I插0，再抗镜像滤波（截止<原Nyquist）\n');
fprintf('3. 有理数重采样: 先插值(I)后抽取(D)，联合设计低通滤波器\n');
fprintf('4. 多相结构: 重采样效率核心，计算量降低至1/D\n');
fprintf('5. 维度鲁棒: 向量运算前强制统一行/列维度，避免MATLAB外积误判\n');
fprintf('6. MATLAB核心函数: resample(首选)、decimate、interp、upfirdn\n');

习题

  1. 设计一个系统，将48kHz的音频信号转换为44.1kHz的CD采样率，比较单级实现和多级实现的性能差异。

  2. 实现一个采样率转换系统，能够根据用户输入的I和D值动态调整滤波器的参数。

  3. 比较不同窗函数（汉明窗、汉宁窗、凯泽窗）对抽取和插值系统性能的影响。

  4. 研究多相结构在实时信号处理系统中的优势，并给出计算复杂度分析。

  5. 设计一个自适应采样率转换系统，能够根据输入信号的频率特性自动选择最佳的抽取/插值因子。

总结

本章详细介绍了多抽样率数字信号处理的基本概念和实现方法。通过MATLAB代码示例，展示了抽取、插值、有理数抽样率转换的原理和实现，对比了不同方法的性能差异。多相结构和多级实现是提高计算效率的重要手段，在实际系统中具有重要应用价值。

关键点总结：

  • 抽取前必须进行抗混叠滤波

  • 插值后必须进行抗镜像滤波

  • 多相结构可显著提高计算效率

  • 多级实现可降低滤波器复杂度

  • MATLAB提供了丰富的多抽样率处理函数

希望本章内容能帮助读者深入理解多抽样率数字信号处理的基本原理和实现方法，为实际应用打下坚实基础。

相关推荐
what丶k2 小时前
深入理解贪心算法：从原理到经典实践
算法·贪心算法·代理模式
郝学胜-神的一滴2 小时前
B站：从二次元到AI创新孵化器的华丽转身 | Google Cloud峰会见闻
开发语言·人工智能·算法
BHXDML2 小时前
数据结构：（三）字符串——从暴力匹配到 KMP 的跨越
数据结构·算法
果粒蹬i2 小时前
从割裂到融合：MATLAB与Python混合编程实战指南
开发语言·汇编·python·matlab
2301_790300962 小时前
嵌入式GPU编程
开发语言·c++·算法
半桔2 小时前
【设计模式】策略模式：可插拔算法，从硬编码到灵活适配，体会“算法解耦“思想
java·c++·算法·设计模式·策略模式
sali-tec2 小时前
C# 基于OpenCv的视觉工作流-章18-图像缩放
图像处理·人工智能·opencv·算法·计算机视觉
2401_841495642 小时前
【LeetCode刷题】LRU缓存
数据结构·python·算法·leetcode·缓存·lru缓存·查找
2401_841495642 小时前
【数据挖掘】Apriori算法
python·算法·数据挖掘·数据集·关联规则挖掘·关联规则·频繁项集挖掘
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05struts2 XML外部实体注入漏洞复现（CVE-2025-68493）06UV安装并设置国内源07在Trae中使用Pencil MCP08Open Code教程（四）| 高级配置与集成09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南