【保姆级详解】K 个一组翻转链表(迭代解法)
K个一组翻转链表 是链表操作类算法题中的经典进阶题,它不仅融合了「链表反转」的核心逻辑,还需要处理分组、边界拼接等复杂场景。本文会从问题拆解、核心思路、代码逐行解析、执行流程模拟四个维度,把这道题的迭代解法讲透,方便你复习时快速理解每一个细节。
一、问题描述
题目要求
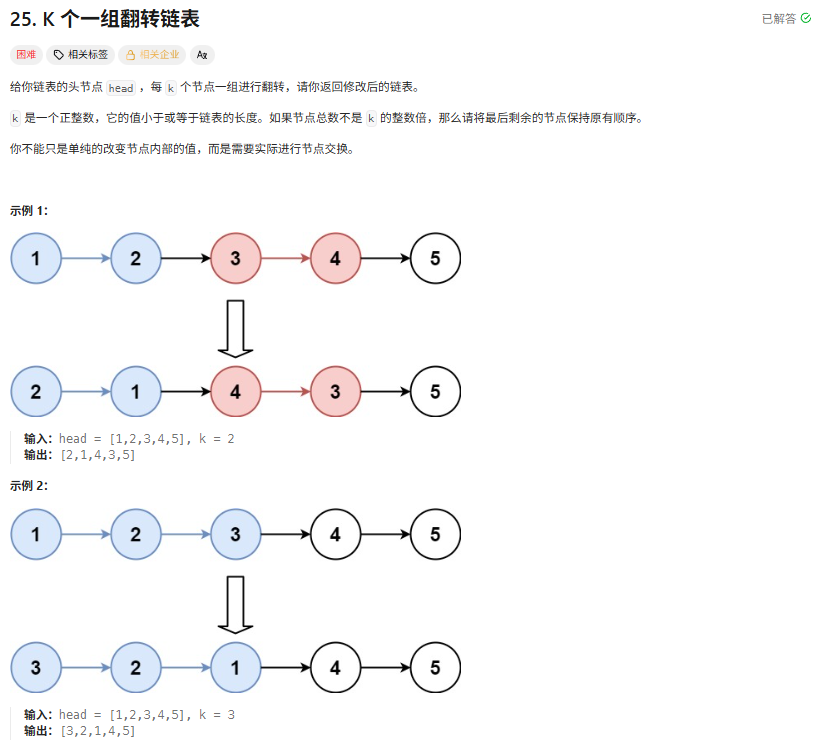
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k是一个正整数,它的值小于或等于链表的长度。- 如果节点总数不是
k的整数倍,那么请将最后剩余的节点保持原有顺序。 - 要求:不能只是单纯改变节点内部的值,而是需要实际进行节点交换。
示例
-
输入:
head = [1,2,3,4,5], k = 2 -
输出:
[2,1,4,3,5] -
输入:
head = [1,2,3,4,5], k = 3 -
输出:
[3,2,1,4,5]
链表节点定义
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/二、核心思路拆解
这道题的核心是「分组反转 + 边界拼接」,可以拆解为 3 个关键步骤:
- 统计链表长度 :确定能分成多少个完整的
k节点组(避免对不足k个的最后一组进行反转); - 虚拟头节点兜底 :用
dummy节点统一 "首组反转" 和 "后续组反转" 的拼接逻辑,避免单独处理头节点; - 分组反转 + 拼接 :
- 对每一组
k个节点执行「链表反转」操作; - 把反转后的组与前一组、后一组正确拼接;
- 更新指针,处理下一组。
- 对每一组
三、完整代码(带详细注释)
java
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
// 步骤1:统计链表总长度,用于判断能分成多少个完整的k组
int n = 0;
for(ListNode cur = head; cur != null; cur = cur.next) {
n++;
}
// 步骤2:创建虚拟头节点,指向原头节点(统一边界处理)
ListNode dummy = new ListNode(0, head);
// p0:每一组待反转节点的「前驱节点」(关键!用于拼接反转后的组)
ListNode p0 = dummy;
// pre/cur:链表反转的经典双指针(pre初始为null,cur初始为头节点)
ListNode pre = null;
ListNode cur = head;
// 步骤3:遍历处理每一个k组(剩余节点数≥k时才反转)
for(; n >= k; n -= k) {
// 步骤4:反转当前k个节点(标准的「链表反转」逻辑)
for(int i = 0; i < k; i++) {
ListNode nxt = cur.next; // 保存cur的下一个节点,避免丢失
cur.next = pre; // 反转cur的指向(指向pre)
pre = cur; // pre后移
cur = nxt; // cur后移
}
// 步骤5:拼接反转后的组(核心!这一步是易错点)
ListNode nxt = p0.next; // 保存当前组反转前的头节点(反转后变成组尾)
p0.next.next = cur; // 让反转后的组尾指向cur(下一组的头/剩余未反转节点)
p0.next = pre; // 让前驱节点p0指向反转后的组头(pre)
p0 = nxt; // 更新p0为当前组的组尾,作为下一组的前驱
}
// 步骤6:返回虚拟头节点的下一个节点(反转后的新头)
return dummy.next;
}
}四、逐行代码解析(复习重点)
1. 统计链表长度
int n = 0;
for(ListNode cur = head; cur != null; cur = cur.next) {
n++;
}- 作用 :计算链表总节点数
n,后续通过n >= k判断是否需要反转当前组(比如n=5, k=2时,能反转 2 组,剩余 1 个节点不处理); - 细节 :遍历过程中不修改原链表,仅做计数,时间复杂度
O(n)。
2. 初始化核心指针
ListNode dummy = new ListNode(0, head);
ListNode p0 = dummy;
ListNode pre = null;
ListNode cur = head;| 指针 | 初始值 | 核心作用 |
|---|---|---|
dummy |
指向原头节点 | 避免单独处理 "第一组反转后头节点变更" 的问题,最终返回 dummy.next 即可; |
p0 |
指向 dummy |
每一组待反转节点的前驱节点,负责把反转后的组拼接到前序链表中; |
pre |
null |
链表反转的 "前一个节点",初始为 null(符合链表反转的初始逻辑); |
cur |
原头节点 head |
链表反转的 "当前节点",从原头节点开始遍历。 |
3. 分组反转的外层循环
for(; n >= k; n -= k) { ... }- 循环条件 :
n >= k表示剩余节点数足够组成一个k组,才执行反转; - n -= k :每处理完一组,剩余节点数减少
k,直到不足k个时停止。
4. 反转当前 k 个节点(经典链表反转)
for(int i = 0; i < k; i++) {
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}- 核心逻辑 :标准的 "原地反转链表",循环
k次仅反转当前组的k个节点; - 关键变量 :
nxt必须提前保存cur.next,否则反转cur.next = pre后会丢失后续节点; - 执行后状态 :
pre:指向当前组反转后的组头;cur:指向下一组的第一个节点(或剩余未反转节点)。
5. 拼接反转后的组(最易错!)
ListNode nxt = p0.next; // ①
p0.next.next = cur; // ②
p0.next = pre; // ③
p0 = nxt; // ④这 4 行是整个代码的核心难点 ,我们用 head=[1,2,3,4,5], k=2 的第一组反转(1→2)为例拆解:
- ①
ListNode nxt = p0.next:p0初始指向dummy,p0.next是1(反转前的组头,反转后变成组尾),用nxt保存这个组尾; - ②
p0.next.next = cur:p0.next是1,cur此时指向3(下一组的头),这一步让反转后的组尾1指向3,避免链表断裂; - ③
p0.next = pre:pre此时指向2(反转后的组头),这一步让p0(dummy)指向2,完成第一组的拼接(dummy→2→1→3→4→5); - ④
p0 = nxt:把p0更新为1(当前组的组尾),作为下一组(3→4)的前驱节点,准备处理下一组。
6. 返回结果
return dummy.next;- 无论第一组是否反转,
dummy.next始终指向最终链表的头节点(避免返回原头节点导致错误)。
五、执行流程模拟(以 head=[1,2,3,4,5], k=2 为例)
为了方便复习时快速回忆,我们模拟完整执行步骤:
| 步骤 | 指针状态 | 链表状态 |
|---|---|---|
| 初始状态 | n=5, dummy→1→2→3→4→5, p0=dummy, pre=null, cur=1 |
dummy→1→2→3→4→5 |
| 第一组反转(i=0/1) | 反转后 pre=2, cur=3 |
1←2 3→4→5(临时断裂) |
| 第一组拼接 | nxt=1, 1→3, dummy→2, p0=1 |
dummy→2→1→3→4→5 |
| 第二组反转(i=0/1) | 反转后 pre=4, cur=5 |
3←4 5(临时断裂) |
| 第二组拼接 | nxt=3, 3→5, 1→4, p0=3 |
dummy→2→1→4→3→5 |
| 循环结束 | n=1 < 2,剩余节点 5 不处理 |
dummy→2→1→4→3→5 |
| 返回结果 | dummy.next=2 |
2→1→4→3→5 |
六、复习关键避坑点
- 拼接时的指针顺序 :必须先保存
p0.next(nxt),再修改p0.next.next,最后修改p0.next,否则会丢失节点引用; - p0 的更新时机 :只有拼接完成后,才能把
p0设为当前组的组尾(nxt),否则会导致下一组前驱节点错误; - 剩余节点处理 :通过
n >= k控制循环,确保最后不足k个的节点不反转; - 虚拟头节点的必要性 :如果没有
dummy,第一组反转后需要单独修改head,逻辑会更复杂。
七、总结(复习速记)
- 核心逻辑 :
统计长度→分组反转→拼接边界,其中「拼接边界」是核心难点; - 关键指针 :
p0:组前驱,负责拼接反转后的组;pre/cur:组内反转的双指针;dummy:统一头节点处理逻辑;
- 执行顺序 :先反转组内节点,再拼接组的首尾,最后更新
p0处理下一组。